Función de distancia con signo

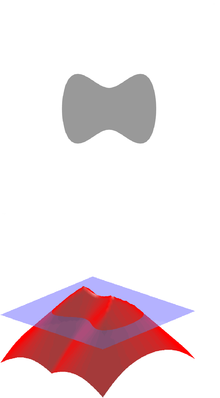
En matemáticas y sus aplicaciones, la función de distancia con signo o campo de distancia con signo (SDF) es la distancia ortogonal de un punto dado x al límite de un conjunto Ω en un espacio métrico (como la superficie de una forma geométrica), con el signo determinado por si x está o no en el interior de Ω. La función tiene valores positivos en los puntos x dentro de Ω, disminuye en valor a medida que x se acerca al límite de Ω donde la función de distancia con signo es cero, y toma valores negativos fuera de Ω. Sin embargo, a veces también se toma la convención alternativa (es decir, negativo dentro de Ω y positivo fuera). El concepto también se conoce a veces con el nombre de función/campo de distancia orientada.

Vamos. Ω ser un subconjunto de un espacio métrico X con métrica d, y ${\displaystyle \partial \Omega }$ sea su límite. La distancia entre un punto x de X y el subconjunto ${\displaystyle \partial \Omega }$ de X se define como de costumbre

${\displaystyle d(x,\partial \Omega)=\inf _{y\in \partial \Omega }d(x,y),}$

Donde ${\displaystyle \inf}$ denota el infimum.

El función de distancia firmada desde un punto x de X a ${\displaystyle \Omega }$ se define por

${\displaystyle f(x)={\begin{cases}d(x,\partial \Omega) reducida{\text{if }x\in \\Omega \\-d(x,\partial \Omega) limitada{\text{if }\,x\notin \Omega.\end{cases}}}}}$

Si Ω es un subconjunto del espacio euclidiano Rⁿ con un límite suave por partes, entonces la función de distancia con signo es diferenciable casi en todas partes, y su gradiente satisface la ecuación eikonal

${\displaystyle Silencio\nabla f arrest=1.}$

Si el límite de Ω es C^k para k ≥ 2 (ver Clases de diferenciabilidad), entonces d es C^k en puntos suficientemente cercanos al límite de Ω. En particular, en el límite f satisface

${\displaystyle \nabla f(x)=N(x),}$

donde N es el campo vectorial normal interno. La función de distancia con signo es, por lo tanto, una extensión diferenciable del campo vectorial normal. En particular, la hessiana de la función de distancia con signo en el límite de Ω da la función de Weingarten.

Si, además, Γ es una región suficientemente cercana al límite de Ω como para que f sea dos veces continuamente diferenciable en ella, entonces existe una fórmula explícita que involucra la función de Weingarten W_x para el jacobiano de variables cambiantes en términos de la función de distancia con signo y el punto límite más cercano. Específicamente, si T(∂Ω, μ) es el conjunto de puntos dentro de la distancia μ del límite de Ω (es decir, el entorno tubular de radio μ), y g es una función absolutamente integrable en Γ, entonces

${\displaystyle \int _{T(\partial \Omega\mu)}g(x)\,dx=\int _{\partial \Omega }\int _{-\mu }g(u+\lambda N(u))\,\det(I-\lambda W_{u})\,d\lambu\$

donde det denota el determinante y dS_u indica que estamos tomando la integral de superficie.

Los algoritmos para calcular la función de distancia con signo incluyen el método de marcha rápida eficiente, el método de barrido rápido y el método de nivelación más general.

Para la representación de vóxeles, un algoritmo rápido para calcular la SDF en la geometría de taxis utiliza tablas de áreas sumadas.

Las funciones de distancia con signo se aplican, por ejemplo, en la representación en tiempo real, por ejemplo, en el método de marcha de rayos SDF y en la visión artificial.

SDF se ha utilizado para describir la geometría de objetos en renderizado en tiempo real, generalmente en un contexto de raymarching, a partir de mediados de la década de 2000. En 2007, Valve utilizó SDF para renderizar fuentes suaves de gran tamaño de píxel (o DPI alto) con aceleración de GPU en sus juegos. El método de Valve no es perfecto, ya que se ejecuta en el espacio rasterizado para evitar la complejidad computacional de resolver el problema en el espacio vectorial (continuo). El texto renderizado a menudo pierde esquinas agudas. En 2014, Behdad Esfahbod presentó un método mejorado. GLyphy de Behdad aproxima las curvas de Bézier de la fuente con splines de arco, aceleradas por técnicas de discretización basadas en cuadrícula (que descartan puntos demasiado lejanos) para ejecutarse en tiempo real.

Se introdujo una versión modificada de SDF como función de pérdida para minimizar el error en la interpenetración de píxeles al renderizar varios objetos. En particular, para cualquier píxel que no pertenezca a un objeto, si se encuentra fuera del objeto en la renderización, no se impone ninguna penalización; si se encuentra fuera, se impone un valor positivo proporcional a su distancia dentro del objeto.

${\displaystyle f(x)={\begin{cases}0 ventaja{\text{if }\,x\in \Omega ^{c}\d(x,\partial \Omega) reducida{\text{if }\,x\in \Omega\end{cases}}$

En 2020, el motor de juegos FOSS Godot 4.0 recibió iluminación global en tiempo real basada en SDF (SDFGI), que se convirtió en un compromiso entre la GI basada en vóxeles más realista y la GI horneada. Su principal ventaja es que se puede aplicar al espacio infinito, lo que permite a los desarrolladores usarlo para juegos de mundo abierto.

En 2023, se lanzó un marco de interfaz de usuario "GPUI" para dibujar todos los elementos de la interfaz de usuario utilizando la GPU, y muchas partes utilizando SDF. El autor afirma haber producido un editor de código Zed que se renderiza a 120 fps. El trabajo hace uso de la lista de primitivas geométricas de Inigo Quilez en SDF, el desenfoque gaussiano aproximado de Evan Wallace (cofundador de Figma) en SDF y un nuevo SDF de rectángulo redondeado.

• Función de distancia
• Método de ajuste de nivel
• Ecuación Eikonal
• Curva paralela (también conocida como curva offset)
• Longitud del arco señalizado
• Zona firmada
• Medida firmada
• Volumen registrado

• Stanley J. Osher y Ronald P. Fedkiw (2003). Métodos de ajuste de nivel y superficies dinámicas implícitas. Springer. ISBN 9780387227467.
• Gilbarg, D.; Trudinger, N. S. (1983). Ecuaciones diferenciales parciales elípticas de la segunda orden. Grundlehren der mathematischen Wissenschaften. Vol. 224 (2a edición). Springer-Verlag. (o el Apéndice de la primera edición de 1977)