Función booleana

En matemáticas, una función booleana es una función cuyos argumentos y resultados asumen valores de un conjunto de dos elementos (normalmente {verdadero, falso}, {0,1} o {-1,1). }). Los nombres alternativos son función de conmutación, utilizada especialmente en la literatura informática más antigua, y función de verdad (o función lógica), utilizada en lógica. Las funciones booleanas son el tema del álgebra booleana y la teoría de conmutación.

Una función booleana toma la forma ${displaystyle f:{0,1}to {0,1}$, donde ${displaystyle {0,1}}$ es conocido como el dominio booleano y ${displaystyle k}$ es un entero no negativo llamado la aridad de la función. En el caso en que ${displaystyle k=0}$, la función es un elemento constante ${displaystyle {0,1}}$. Una función booleana con múltiples salidas, ${displaystyle f:{0,1} {k}to {0,1} {m}}$ con ${displaystyle m]$ es un vectorial o valor vectorial Función booleana (una S-box en criptografía simétrica).

Hay ${displaystyle 2^{2^{k}}$ diferentes funciones booleanas con ${displaystyle k}$ argumentos; igual al número de diferentes tablas de verdad con ${displaystyle 2^{k}$ entradas.

Cada uno ${displaystyle k}$- La función booleana puede expresarse como una fórmula proposicional en ${displaystyle k}$ variables ${displaystyle x_{1},...$, y dos fórmulas proposiciones son lógicamente equivalentes si y sólo si expresan la misma función booleana.

Ejemplos

Las funciones booleanas simétricas rudimentarias (conjuntivos lógicos o puertas lógicas) son:

• NO, negación o complemento - que recibe una entrada y devuelve la verdad cuando esa entrada es falsa ("no")
• Y o conjunción - verdadero cuando todas las entradas son verdaderas ("tanto")
• OR o disyunción - verdadero cuando cualquier entrada es verdadera ("ya sea")
• XOR o disyunción exclusiva - verdadero cuando una de sus entradas es verdadera y la otra es falsa ("no igual")
• Apoplejía NAND o Sheffer - verdadero cuando no es el caso que todas las entradas son verdaderas ("no ambas")
• NOR o lógica ni - verdadero cuando ninguna de las entradas son verdaderas ("no")
• XNOR o igualdad lógica - verdadero cuando ambas entradas son las mismas ("igual")

Un ejemplo de una función más complicada es la función mayoritaria (de un número impar de entradas).

Representación

Una función booleana se puede especificar de varias maneras:

• Tabla de la verdad: enumerar explícitamente su valor para todos los valores posibles de los argumentos
  • Diagrama de Marquand: valores de tabla de la verdad dispuestos en una cuadrícula bidimensional (utilizado en un mapa de Karnaugh)
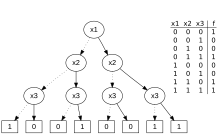
  • Esquema de decisión binaria, enumerando los valores de tabla de la verdad en el fondo de un árbol binario
  • Diagrama de Venn, representando los valores de tabla de verdad como una coloración de regiones del plano

Algebraicamente, como fórmula proposicional que utiliza funciones booleanas rudimentarias:

• Negation normal form, an arbitrary mix of AND and ORs of the arguments and their complements
• Forma normal disyuntiva, como OR de ANDs de los argumentos y sus complementos
• Forma normal conjuntiva, como AND de ORs de los argumentos y sus complementos
• Forma normal canónica, una fórmula estandarizada que identifica singularmente la función:
  • Forma normal algebraica o polinomio Zhegalkin, como XOR de ANDs de los argumentos (sin complementos permitidos)
  • Total (canónica) forma normal disyuntiva, una OR de ANDs que contienen cada argumento o complemento (minterms)
  • Total (canónico) forma normal conjuntiva, una AND de ORs que contienen cada argumento o complemento (maxterms)
  • Blake forma canónica, el OR de todos los principales implicantes de la función

Las fórmulas booleanas también se pueden mostrar como un gráfico:

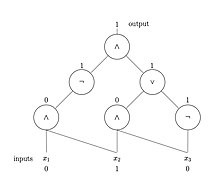
• Gráfico acíclico dirigido proposición
  • Diagrama de circuito digital de las puertas lógicas, un circuito booleano
  • Gráfico de inversor, usando sólo Y NO

Para optimizar los circuitos electrónicos, las fórmulas booleanas se pueden minimizar utilizando el algoritmo de Quine-McCluskey o el mapa de Karnaugh.

Análisis

Propiedades

Una función booleana puede tener una variedad de propiedades:

• Constante: Siempre es verdadero o siempre falso independientemente de sus argumentos.
• Monotone: para cada combinación de valores de argumento, cambiar un argumento de falso a verdadero sólo puede hacer que la salida cambie de falso a verdadero y no de verdadero a falso. Se dice que una función no se comió en una determinada variable si es monotona con respecto a los cambios en esa variable.
• Linear: para cada variable, cambiar el valor de la variable siempre marca una diferencia en el valor de la verdad o nunca marca una diferencia (una función de paridad).
• Simétrico: el valor no depende del orden de sus argumentos.
• Read-once: Se puede expresar conjunción, disyunción y negación con una sola instancia de cada variable.
• Equilibrado: si su tabla de la verdad contiene un número igual de ceros y uno. El peso Hamming de la función es el número de los en la tabla de la verdad.
• Bent: sus derivados son todos equilibrados (el espectro de autocorrelación es cero)
• Correlación inmune a mp orden: si la salida no está relacionada con todas las combinaciones (linear) de la mayoría m argumentaciones
• Evasivo: si la evaluación de la función siempre requiere el valor de todos los argumentos
• Una función booleana es una Función de almacenamiento si se puede utilizar para crear (por composición) cualquier función booleana arbitraria (ver la integridad funcional)
• El grado algebraico de una función es el orden del orden más alto monomial en su forma algebraica normal

La complejidad del circuito intenta clasificar las funciones booleanas con respecto al tamaño o profundidad de los circuitos que pueden computar.

Funciones derivadas

Una función booleana se puede descomponer utilizando el teorema de expansión de Boole en Shannon cofactores positivos y negativos (expansión de Shannon), que son los (k-1) Funciones -arias resultantes de fijar uno de los argumentos (a cero o uno). Las funciones generales (k-arias) obtenidas imponiendo una restricción lineal a un conjunto de entradas (un subespacio lineal) se conocen como subfunciones.

La derivada booleana de la función para uno de los argumentos es una función (k-1)-aria que es verdadera cuando la salida de la función es sensible a la variable de entrada elegida; es el XOR de los dos cofactores correspondientes. En una expansión de Reed-Muller se utilizan una derivada y un cofactor. El concepto se puede generalizar como una derivada k-aria en la dirección dx, obtenida como la diferencia (XOR) de la función en x y x + dx.

La transformada de Möbius (o transformada de Boole-Möbius) de una función booleana es el conjunto de coeficientes de su polinomio (forma normal algebraica), en función de la vectores exponentes monomios. Es una transformación autoinversa. Se puede calcular de manera eficiente utilizando un algoritmo de mariposa ("Transformada Rápida de Möbius"), análogo a la Transformada Rápida de Fourier. Las funciones booleanas coincidentes son iguales a su transformada de Möbius, es decir, los valores de su tabla de verdad (minterm) son iguales a sus coeficientes algebraicos (monomio). Hay 2^2^(k−1) funciones coincidentes de k argumentos.

Análisis criptográfico

La transformada de Walsh de una función booleana es una función k-aria con valores enteros que proporciona los coeficientes de una descomposición en funciones lineales (funciones de Walsh), análoga a la descomposición de funciones con valores reales en armónicos mediante la transformada de Fourier. Su cuadrado es el espectro de potencia o espectro de Walsh. El coeficiente de Walsh de un vector de un solo bit es una medida de la correlación de ese bit con la salida de la función booleana. El coeficiente de Walsh máximo (en valor absoluto) se conoce como linealidad de la función. El número más alto de bits (orden) para el cual todos los coeficientes de Walsh son 0 (es decir, las subfunciones están equilibradas) se conoce como resiliencia, y se dice que la función es inmune a la correlación de ese orden. Los coeficientes de Walsh juegan un papel clave en el criptoanálisis lineal.

La autocorrelación de una función booleana es una función k-aria con valores enteros que proporciona la correlación entre un cierto conjunto de cambios en las entradas y la salida de la función. Para un vector de bits dado, está relacionado con el peso de Hamming de la derivada en esa dirección. El coeficiente de autocorrelación máximo (en valor absoluto) se conoce como indicador absoluto. Si todos los coeficientes de autocorrelación son 0 (es decir, las derivadas están equilibradas) para un cierto número de bits, entonces se dice que la función satisface el criterio de propagación en ese orden; si todos son cero, entonces la función es una función inclinada. Los coeficientes de autocorrelación juegan un papel clave en el criptoanálisis diferencial.

Los coeficientes de Walsh de una función booleana y sus coeficientes de autocorrelación están relacionados por el equivalente del teorema de Wiener-Khinchin, que establece que la autocorrelación y el espectro de potencia son un par de transformada de Walsh.

Tabla de aproximación lineal

Estos conceptos se pueden extender naturalmente a funciones booleanas vectoriales considerando sus bits de salida (coordenadas) individualmente, o más detalladamente, observando el conjunto de todas las funciones lineales. de bits de salida, conocidos como sus componentes. El conjunto de transformadas de Walsh de los componentes se conoce como Tabla de aproximación lineal (LAT) o matriz de correlación; describe la correlación entre diferentes combinaciones lineales de bits de entrada y salida. El conjunto de coeficientes de autocorrelación de los componentes es la tabla de autocorrelación, relacionada mediante una transformada de Walsh de los componentes con la Tabla de distribución de diferencias (DDT), más utilizada, que enumera las correlaciones. entre diferencias en bits de entrada y salida (ver también: S-box).

Forma polinómica real

En el hipercubo unitario

Cualquier función booleana ${displaystyle f(x):{0,1}{n}rightarrow {0,1}$ puede ser extendido (interpolado) al dominio real por un polino multilineal en ${displaystyle mathbb {R} {} {}} {fn}}$, construido resumiendo los valores de tabla de verdad multiplicados por polinomios indicador:

$${displaystyle f^{*}(x)=sum _{ain {{0,1}} {n}f(a)prod - ¿Qué? ¿Por qué?$$

${displaystyle xoplus y}$

$${displaystyle 0(1-x)(1-y)+1x(1-y)+1(1-x)y+0xy}$$

$${displaystyle x+y-2xy}$$

${displaystyle 1-x}$

${displaystyle xy}$

${displaystyle x+y-xy}$

Las expresiones directas para los coeficientes del polinomio se pueden derivar tomando una derivada apropiada:

$${f} {f} {f}f}f} {f}f} {f}f} {f} {f}f} {f}}f}f}f}f}f}f} {f}f} {f}f}f}}f}f}f}f}f}}f}f}f}}}f}cH00}cH00}}}}}}}}}cH00}cH00}}cH00}cH00}cH00}}}f}}}}}}}}}}}}}}}}}}}}}}}f}$$

$${displaystyle f^{*}(m)=sum _{asubseteq m}(-1)^{Principalidad sobre la vida eterna.$$

${displaystyle Silencioso$

${displaystyle a}$

$${displaystyle {hat {f}(m)=bigoplus _{asubseteq m}f(a)}$$

Cuando el dominio está restringido al hipercubo n-dimensional ${displaystyle [0,1]$, el polinomio ${displaystyle f^{*}(x):[0,1]^{n}rightarrow [0,1]}$ da la probabilidad de un resultado positivo cuando la función booleana f se aplica a n variables independientes al azar (Bernoulli) con probabilidades individuales x. Un caso especial de este hecho es el lema piling-up para las funciones de paridad. La forma polinomio de una función booleana también se puede utilizar como su extensión natural a la lógica borrosa.

Sobre el hipercubo simétrico

A menudo, el dominio booleano se toma como ${displaystyle {-1,1}}$, con asignación falsa ("0") a 1 y verdadero ("1") a -1 (ver Análisis de funciones booleanas). El polinomio correspondiente a ${displaystyle g(x):{-1,1}{n}rightarrow {-1,1}}$ es entonces dado por:

$${displaystyle g^{*}(x)=sum _{ain {fnMicrosoft Sans Serif} ¿Por qué? {1-x_{i}{2}prod ¿Qué? {1+x_{i} {2}}}}$$

${displaystyle E(X)=P(X=1)-P(X=-1)in [-1,1]}$

Aplicaciones

Las funciones booleanas juegan un papel básico en cuestiones de teoría de la complejidad, así como en el diseño de procesadores para computadoras digitales, donde se implementan en circuitos electrónicos mediante puertas lógicas.

Las propiedades de las funciones booleanas son críticas en criptografía, particularmente en el diseño de algoritmos de clave simétrica (ver cuadro de sustitución).

En la teoría de juegos cooperativos, las funciones booleanas monótonas se denominan juegos simples (juegos de votación); esta noción se aplica para resolver problemas en la teoría de la elección social.