Fuerza Coriolis

En física, la fuerza de Coriolis es una fuerza inercial o ficticia que actúa sobre objetos en movimiento dentro de un marco de referencia que gira con respecto a un marco inercial. En un marco de referencia con rotación en el sentido de las agujas del reloj, la fuerza actúa a la izquierda del movimiento del objeto. En uno con rotación en sentido antihorario (o antihorario), la fuerza actúa hacia la derecha. La desviación de un objeto debido a la fuerza de Coriolis se denomina efecto de Coriolis. Aunque reconocida previamente por otros, la expresión matemática de la fuerza de Coriolis apareció en un artículo de 1835 del científico francés Gaspard-Gustave de Coriolis, en relación con la teoría de las ruedas hidráulicas. A principios del siglo XX, el término fuerza de Coriolis comenzó a utilizarse en relación con la meteorología.
Las leyes de movimiento de Newton describen el movimiento de un objeto en un marco de referencia inercial (sin aceleración). Cuando las leyes de Newton se transforman a un marco de referencia giratorio, aparecen las aceleraciones de Coriolis y centrífuga. Cuando se aplica a objetos con masas, las fuerzas respectivas son proporcionales a sus masas. La magnitud de la fuerza de Coriolis es proporcional a la velocidad de rotación y la magnitud de la fuerza centrífuga es proporcional al cuadrado de la velocidad de rotación. La fuerza de Coriolis actúa en una dirección perpendicular a dos cantidades: la velocidad angular del marco giratorio en relación con el marco inercial y la velocidad del cuerpo en relación con el marco giratorio, y su magnitud es proporcional a la velocidad del objeto en el marco giratorio (más precisamente, a la componente de su velocidad que es perpendicular al eje de rotación). La fuerza centrífuga actúa hacia el exterior en dirección radial y es proporcional a la distancia del cuerpo al eje del marco giratorio. Estas fuerzas adicionales se denominan fuerzas de inercia, fuerzas ficticias o pseudofuerzas. Al introducir estas fuerzas ficticias en un marco de referencia giratorio, las leyes de movimiento de Newton se pueden aplicar al sistema giratorio como si fuera un sistema inercial; estas fuerzas son factores de corrección que no se requieren en un sistema no giratorio.
En el uso popular (no técnico) del término "efecto Coriolis", el marco de referencia giratorio implícito es casi siempre la Tierra. Debido a que la Tierra gira, los observadores terrestres deben tener en cuenta la fuerza de Coriolis para analizar correctamente el movimiento de los objetos. La Tierra completa una rotación por cada ciclo día/noche, por lo que para los movimientos de los objetos cotidianos, la fuerza de Coriolis suele ser bastante pequeña en comparación con otras fuerzas; sus efectos generalmente se vuelven perceptibles solo para movimientos que ocurren a grandes distancias y largos períodos de tiempo, como el movimiento a gran escala del aire en la atmósfera o el agua en el océano; o donde la alta precisión es importante, como la artillería de largo alcance o las trayectorias de los misiles. Dichos movimientos están limitados por la superficie de la Tierra, por lo que generalmente solo es importante la componente horizontal de la fuerza de Coriolis. Esta fuerza hace que los objetos en movimiento sobre la superficie de la Tierra se desvíen hacia la derecha (con respecto a la dirección de desplazamiento) en el hemisferio norte y hacia la izquierda en el hemisferio sur. El efecto de deflexión horizontal es mayor cerca de los polos, ya que la tasa de rotación efectiva alrededor de un eje vertical local es mayor allí y disminuye a cero en el ecuador. En lugar de fluir directamente de las áreas de alta presión a las de baja presión, como lo harían en un sistema no giratorio, los vientos y las corrientes tienden a fluir hacia la derecha de esta dirección al norte del ecuador (en sentido contrario a las agujas del reloj) y hacia la izquierda de esta dirección al sur. de ella (en el sentido de las agujas del reloj). Este efecto es responsable de la rotación y, por lo tanto, de la formación de ciclones (ver efectos de Coriolis en meteorología).
Para una explicación intuitiva del origen de la fuerza de Coriolis, considere un objeto, obligado a seguir la superficie de la Tierra y moviéndose hacia el norte en el hemisferio norte. Visto desde el espacio exterior, el objeto no parece ir hacia el norte, sino que tiene un movimiento hacia el este (gira hacia la derecha junto con la superficie de la Tierra). Cuanto más al norte viaja, menor es el "radio de su paralelo (latitud)" (la distancia mínima desde el punto de la superficie al eje de rotación, que está en un plano ortogonal al eje), y por lo tanto más lento es el movimiento hacia el este de su superficie. A medida que el objeto se mueve hacia el norte, hacia latitudes más altas, tiende a mantener la velocidad hacia el este con la que comenzó (en lugar de disminuir la velocidad para igualar la velocidad reducida hacia el este de los objetos locales en la superficie de la Tierra), por lo que vira hacia el este. (es decir, a la derecha de su movimiento inicial).
Aunque no es obvio a partir de este ejemplo, que considera el movimiento hacia el norte, la deflexión horizontal ocurre igualmente para los objetos que se mueven hacia el este o hacia el oeste (o en cualquier otra dirección). Sin embargo, la teoría de que el efecto determina la rotación del agua de drenaje en una bañera, lavabo o inodoro doméstico de tamaño típico ha sido refutada repetidamente por los científicos modernos; la fuerza es insignificantemente pequeña en comparación con las muchas otras influencias en la rotación.
Historia

El científico italiano Giovanni Battista Riccioli y su asistente Francesco Maria Grimaldi describieron el efecto en relación con la artillería en el Almagestum Novum de 1651, escribiendo que la rotación de la Tierra debería hacer que una bala de cañón disparada hacia el norte se desviara hacia el este. En 1674, Claude François Milliet Dechales describió en su Cursus seu Mundus Mathematicus cómo la rotación de la Tierra debería provocar una desviación en las trayectorias tanto de los cuerpos que caen como de los proyectiles dirigidos hacia uno de los planetas. postes Riccioli, Grimaldi y Dechales describieron el efecto como parte de un argumento contra el sistema heliocéntrico de Copérnico. En otras palabras, argumentaron que la rotación de la Tierra debería crear el efecto, por lo que no detectar el efecto era evidencia de una Tierra inmóvil. La ecuación de aceleración de Coriolis fue derivada por Euler en 1749, y el efecto fue descrito en las ecuaciones de marea de Pierre-Simon Laplace en 1778.
Gaspard-Gustave Coriolis publicó un artículo en 1835 sobre el rendimiento energético de las máquinas con piezas giratorias, como las ruedas hidráulicas. Ese documento consideró las fuerzas suplementarias que se detectan en un marco de referencia giratorio. Coriolis dividió estas fuerzas suplementarias en dos categorías. La segunda categoría contenía una fuerza que surge del producto cruzado de la velocidad angular de un sistema de coordenadas y la proyección de la velocidad de una partícula en un plano perpendicular al eje de rotación del sistema. Coriolis se refirió a esta fuerza como la "fuerza centrífuga compuesta" por sus analogías con la fuerza centrífuga ya considerada en la categoría uno. El efecto se conocía a principios del siglo XX como "aceleración de Coriolis", y en 1920 como "fuerza de Coriolis".
En 1856, William Ferrel propuso la existencia de una celda de circulación en las latitudes medias con el aire desviado por la fuerza de Coriolis para crear los vientos predominantes del oeste.
La comprensión de la cinemática de cómo afecta exactamente la rotación de la Tierra al flujo de aire fue parcial al principio. A fines del siglo XIX, se entendió el alcance completo de la interacción a gran escala de la fuerza de gradiente de presión y la fuerza de desviación que al final hace que las masas de aire se muevan a lo largo de las isobaras.
Fórmula
En la mecánica newtoniana, la ecuación de movimiento de un objeto en un marco de referencia inercial es
- F=ma{displaystyle {boldsymbol {F}=m{boldsymbol {a}}
Donde F{displaystyle {boldsymbol {F}} es la suma vectorial de las fuerzas físicas que actúan en el objeto, m{displaystyle m} es la masa del objeto, y a{displaystyle {boldsymbol {a}} es la aceleración del objeto relativo al marco de referencia inercial.
Transformando esta ecuación a un marco de referencia girando alrededor de un eje fijo a través del origen con velocidad angular ⋅ ⋅ {displaystyle {boldsymbol {omega } con velocidad de rotación variable, la ecuación toma la forma
- F.=F− − md⋅ ⋅ dt× × r.− − 2m⋅ ⋅ × × v.− − m⋅ ⋅ × × ()⋅ ⋅ × × r.)=ma.{displaystyle {begin{aligned}{boldsymbol {F'} limit={boldsymbol {F}-m{frac} {fnK} {boldsymbol {omega {fnMicrosoft Sans Serif} 2m{boldsymbol {omega }times {boldsymbol {v'}-m{boldsymbol {omega }times ({boldsymbol {omega }times {boldsymbol {r'}})\\\\\\\\fnK}fnK}}}fnfnunci}}}}fnfnKfnKcH009}}}}fnKfnMinKfnKfnKfnMinKfnMinKfnMinMinMinMinMinMinMinMinMinMinMinMinMinMinMinMinMinMinMinMinMinMinMinMinMinMinMinMinMinMinMinMinkassssssssssssssssssssssssssssipsssssssssssssssssssssssssssss
dónde
- F{displaystyle {boldsymbol {F}} es la suma vectorial de las fuerzas físicas que actúan en el objeto
- ⋅ ⋅ {displaystyle {boldsymbol {omega } es la velocidad angular, del marco de referencia giratorio relativo al marco inercial
- r.{displaystyle {boldsymbol {r}}} es el vector de posición del objeto relativo al marco de referencia giratorio
- v.{displaystyle {boldsymbol}} es la velocidad del objeto relativo al marco de referencia giratorio
- a.{displaystyle {boldsymbol {a}} es la aceleración del objeto relativo al marco de referencia giratorio
Las fuerzas ficticias, tal como se perciben en el marco giratorio, actúan como fuerzas adicionales que contribuyen a la aceleración aparente al igual que las fuerzas externas reales. Los términos de fuerza ficticios de la ecuación son, de izquierda a derecha:
- Fuerza Euler, − − md⋅ ⋅ dt× × r.{displaystyle -m{frac {mathrm} {boldsymbol {omega {fnMicrosoft Sans Serif} {fnMicrosoft Sans Serif}
- Fuerza Coriolis, − − 2m()⋅ ⋅ × × v.){displaystyle -2m({boldsymbol {omega }times {boldsymbol {v'}}}}
- Fuerza centrífuga, − − m⋅ ⋅ × × ()⋅ ⋅ × × r.){displaystyle -m{boldsymbol {omega }times ({boldsymbol {omega }times {boldsymbol {r'})}
Observe el Euler y las fuerzas centrífugas dependen del vector de posición r.{displaystyle {boldsymbol {r}}} del objeto, mientras que la fuerza Coriolis depende de la velocidad del objeto v.{displaystyle {boldsymbol}} medida en el marco de referencia giratorio. Como se esperaba, para un marco de referencia inercial no rotativo ()⋅ ⋅ =0){displaystyle ({boldsymbol {omega }=0)} la fuerza Coriolis y todas las demás fuerzas ficticias desaparecen. Las fuerzas también desaparecen para la masa cero ()m=0){displaystyle (m=0)}.
Como la fuerza de Coriolis es proporcional a un producto cruzado de dos vectores, es perpendicular a ambos vectores, en este caso la velocidad del objeto y el vector de rotación del marco. Por lo tanto, se sigue que:
- si la velocidad es paralela al eje de rotación, la fuerza Coriolis es cero. Por ejemplo, en la Tierra, esta situación ocurre para un cuerpo en el ecuador que se mueve al norte o al sur en relación con la superficie de la Tierra.
- si la velocidad es directa hacia el eje, la fuerza Coriolis está en la dirección de la rotación local. Por ejemplo, en la Tierra, esta situación ocurre para un cuerpo en el ecuador que cae hacia abajo, como en la ilustración de Dechales arriba, donde la bola caída viaja más al este que la torre.
- si la velocidad es directa desde el eje, la fuerza Coriolis está en contra de la dirección de la rotación local. En el ejemplo de la torre, una bola lanzada hacia arriba se movería hacia el oeste.
- si la velocidad está en la dirección de la rotación, la fuerza Coriolis está hacia fuera del eje. Por ejemplo, en la Tierra, esta situación ocurre para un cuerpo en el Ecuador que se mueve hacia el este en relación con la superficie de la Tierra. Se movería hacia arriba como lo vio un observador en la superficie. Este efecto (ver Eötvös efecto abajo) fue discutido por Galileo Galilei en 1632 y por Riccioli en 1651.
- si la velocidad está en contra de la dirección de la rotación, la fuerza Coriolis está hacia el eje. Por ejemplo, en la Tierra, esta situación ocurre para un cuerpo en el Ecuador que se mueve hacia el oeste, que se desviaría hacia abajo como lo ve un observador.
Escalas de longitud y número de Rossby
Las escalas de tiempo, espacio y velocidad son importantes para determinar la importancia de la fuerza Coriolis. Si la rotación es importante en un sistema se puede determinar por su número de Rossby, que es la relación de la velocidad, U, de un sistema al producto del parámetro Coriolis, f=2⋅ ⋅ pecado φ φ {displaystyle f=2omega sin varphi ,}, y la escala de longitud, L, de la moción:
- Ro=UfL.{displaystyle Ro={frac {f}}
El número de Rossby es la relación entre las fuerzas de inercia y las de Coriolis. Un número de Rossby pequeño indica que un sistema está fuertemente afectado por las fuerzas de Coriolis, y un número de Rossby grande indica un sistema en el que dominan las fuerzas de inercia. Por ejemplo, en los tornados, el número de Rossby es grande, en los sistemas de baja presión es bajo y en los sistemas oceánicos es de alrededor de 1. Como resultado, en los tornados la fuerza de Coriolis es insignificante y el equilibrio es entre la presión y las fuerzas centrífugas.. En los sistemas de baja presión, la fuerza centrífuga es insignificante y el equilibrio se da entre las fuerzas de Coriolis y de presión. En los océanos las tres fuerzas son comparables.
Un sistema atmosférico que se mueve a U = 10 m/s (22 mph) ocupando una distancia espacial de L = 1000 km (621 mi), tiene un número de Rossby de aproximadamente 0,1.
Un lanzador de béisbol puede lanzar la pelota a U = 45 m/s (100 mph) a una distancia de L = 18,3 m (60 pies). El número de Rossby en este caso sería 32.000 (en la latitud 31°47'46.382").
A los jugadores de béisbol no les importa en qué hemisferio están jugando. Sin embargo, un misil no guiado obedece exactamente a la misma física que una pelota de béisbol, pero puede viajar lo suficientemente lejos y estar en el aire el tiempo suficiente para experimentar el efecto de la fuerza de Coriolis. Los proyectiles de largo alcance en el hemisferio norte aterrizaron cerca, pero a la derecha, de donde apuntaban hasta que esto se notó. (Los disparados en el hemisferio sur aterrizaron a la izquierda). De hecho, fue este efecto el que primero llamó la atención del propio Coriolis.
Casos simples
Pelota lanzada en un carrusel giratorio
La figura ilustra una pelota lanzada desde las 12:00 en punto hacia el centro de un carrusel que gira en sentido antihorario. A la izquierda, un observador estacionario ve la pelota sobre el carrusel, y la pelota viaja en línea recta hacia el centro, mientras que el lanzador de pelotas gira en sentido contrario a las agujas del reloj con el carrusel. A la derecha, un observador ve la pelota girando con el carrusel, por lo que el lanzador de la pelota parece quedarse a las 12:00 en punto. La figura muestra cómo se puede construir la trayectoria de la pelota vista por el observador giratorio.
A la izquierda, dos flechas ubican la pelota en relación con el lanzador de pelota. Una de estas flechas va desde el lanzador hasta el centro del carrusel (proporcionando la línea de visión del lanzador de la pelota), y las otras apuntan desde el centro del carrusel hasta la pelota. (Esta flecha se acorta a medida que la pelota se acerca al centro). Se muestra una versión desplazada de las dos flechas punteadas.
A la derecha se muestra este mismo par de flechas punteadas, pero ahora el par está rotado rígidamente de modo que la flecha correspondiente a la línea de visión del lanzador de bolas hacia el centro del carrusel esté alineada con las 12:00 o&# 39;reloj. La otra flecha del par ubica la bola en relación con el centro del carrusel, proporcionando la posición de la bola tal como la ve el observador giratorio. Siguiendo este procedimiento para varias posiciones, la trayectoria en el marco de referencia giratorio se establece como se muestra en la trayectoria curva en el panel de la derecha.
La pelota viaja en el aire y no hay fuerza neta sobre ella. Para el observador estacionario, la pelota sigue una trayectoria en línea recta, por lo que no hay problema para cuadrar esta trayectoria con una fuerza neta cero. Sin embargo, el observador giratorio ve un camino curvo. La cinemática insiste en que debe estar presente una fuerza (que empuja hacia la derecha de la dirección instantánea de viaje para una rotación en sentido contrario a las agujas del reloj) para causar esta curvatura, por lo que el observador giratorio es forzado a invocar una combinación de fuerzas centrífugas y de Coriolis para proporcionar la fuerza neta requerida para causar la trayectoria curva.
Pelota rebotada

La figura describe una situación más compleja en la que la pelota lanzada sobre un plato giratorio rebota en el borde del carrusel y luego regresa al lanzador, quien atrapa la pelota. El efecto de la fuerza de Coriolis en su trayectoria se vuelve a mostrar visto por dos observadores: un observador (denominado "cámara") que gira con el carrusel y un observador inercial. La figura muestra una vista de pájaro basada en la misma velocidad de la bola en las trayectorias de avance y retorno. Dentro de cada círculo, los puntos trazados muestran los mismos puntos de tiempo. En el panel de la izquierda, desde el punto de vista de la cámara en el centro de rotación, el lanzador (carita sonriente) y la barandilla están en ubicaciones fijas, y la bola hace un arco muy considerable en su viaje hacia la barandilla, y toma una ruta más directa en el camino de regreso. Desde el punto de vista del lanzador de la pelota, la pelota parece regresar más rápido de lo que fue (porque el lanzador gira hacia la pelota en el vuelo de regreso).
En el carrusel, en lugar de lanzar la pelota directamente a una barandilla para que rebote, el lanzador debe lanzar la pelota hacia la derecha del objetivo y la cámara parece entonces que la pelota gira continuamente hacia la izquierda de su dirección de viaje para llegar a la barandilla (izquierda porque el carrusel está girando en el sentido de las agujas del reloj). La bola parece llevar hacia la izquierda desde la dirección de desplazamiento tanto en la trayectoria de ida como en la de vuelta. La trayectoria curva exige que este observador reconozca una fuerza neta hacia la izquierda sobre la pelota. (Esta fuerza es 'ficticia' porque desaparece para un observador estacionario, como se analiza en breve). Para algunos ángulos de lanzamiento, una trayectoria tiene partes donde la trayectoria es aproximadamente radial, y la fuerza de Coriolis es la principal responsable de la desviación aparente de la bola (la fuerza centrífuga es radial desde el centro de rotación y causa poca desviación en estos segmentos). Sin embargo, cuando una trayectoria se aleja de la radial, la fuerza centrífuga contribuye significativamente a la desviación.
La trayectoria de la pelota por el aire es recta cuando la ven los observadores que están parados en el suelo (panel derecho). En el panel derecho (observador estacionario), el lanzador de la pelota (cara sonriente) está a las 12 en punto y el riel desde el que rebota la pelota está en la posición 1. Desde el punto de vista del espectador inercial, las posiciones 1, 2, y 3 se ocupan en secuencia. En la posición 2, la pelota golpea la banda y en la posición 3, la pelota regresa al lanzador. Se siguen trayectorias en línea recta porque la pelota está en vuelo libre, por lo que este observador requiere que no se aplique ninguna fuerza neta.
Aplicado a la Tierra
La aceleración que afecta el movimiento del aire "deslizando" sobre la superficie de la Tierra es la componente horizontal del término de Coriolis
- − − 2Ω Ω × × v{displaystyle -2,{boldsymbol {Omega times v}}
Esta componente es ortogonal a la velocidad sobre la superficie de la Tierra y viene dada por la expresión
- ⋅ ⋅ v2pecado φ φ {displaystyle omega ,v 2,sin phi }
dónde
- ⋅ ⋅ {displaystyle omega } es la tasa de giro de la Tierra
- φ φ {displaystyle phi } es la latitud, positiva en el hemisferio norte y negativa en el hemisferio sur
En el hemisferio norte, donde el signo es positivo, esta fuerza/aceleración, vista desde arriba, está a la derecha de la dirección del movimiento, en el hemisferio sur, donde el signo es negativo, esta fuerza/aceleración está a la izquierda de la dirección del movimiento
Esfera giratoria
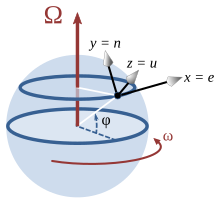
Considere una ubicación con latitud φ en una esfera que gira alrededor del eje norte-sur. Se configura un sistema de coordenadas local con el eje x horizontalmente hacia el este, el eje y horizontalmente hacia el norte y el eje z verticalmente hacia arriba. El vector de rotación, la velocidad de movimiento y la aceleración de Coriolis expresados en este sistema de coordenadas local (enumerando los componentes en el orden este (e), norte (n) y hacia arriba (u)) son:
- Ω Ω =⋅ ⋅ ()0# φ φ pecado φ φ ),{displaystyle {boldsymbol ################################################################################################################################################################################################################################################################ }=omega {begin{pmatrix}\cos varphi\\sin varphiend{pmatrix}}}\ v=()vevnvu),{displaystyle {boldsymbol {fn}={begin {pmatrix}v_{e}v_{n}g_{u}end{pmatrix}}}}} {}} {f}}}} {f}}}} {f}}}}} {f}}}}}}} {f}}}}}}}}}}} {
- aC=− − 2Ω Ω × × v=2⋅ ⋅ ()vnpecado φ φ − − vu# φ φ − − vepecado φ φ ve# φ φ ).{displaystyle {boldsymbol {a}_{}=-2{boldsymbol {Omega times v}=2,omega ,{begin{pmatrix}v_{n}sin varphi -v_{u}cos varphi \-v_{e}sin varphi \v_{e}cos varphi end{pmatrix}}
Al considerar la dinámica atmosférica o oceánica, la velocidad vertical es pequeña, y el componente vertical de la aceleración Coriolis (ve# φ φ {displaystyle v_{e}cos varphi }) es pequeño en comparación con la aceleración debido a la gravedad (g, aproximadamente 9,81 m/s2 (32,2 pies/s2) cerca de la superficie de la Tierra). Para tales casos, sólo importan los componentes horizontales (este y norte). La restricción de lo anterior al plano horizontal es (ajustar vu= 0):
- v=()vevn),{displaystyle {boldsymbol {}={begin {pmatrix}v_{e}v_{n}end{pmatrix}}} ac=()vn− − ve)f,{displaystyle {boldsymbol {fn} {fn} {fn}\fn}\fn}fn} {fn} {fn}}fn} f
Donde f=2⋅ ⋅ pecado φ φ {displaystyle f=2omega sin varphi ,} se llama el parámetro Coriolis.
Al establecer vn = 0, se puede ver inmediatamente que (para φ y ω positivos) un movimiento hacia el este resulta en una aceleración hacia el sur. De manera similar, al establecer ve = 0, se ve que un movimiento hacia el norte da como resultado una aceleración hacia el este.
En general, observado horizontalmente, mirando a lo largo de la dirección del movimiento que causa la aceleración, la aceleración siempre se gira 90° a la derecha (para φ positivo) y es del mismo tamaño independientemente de la orientación horizontal.
Como caso diferente, considere el ajuste de movimiento ecuatorial φ = 0°. En este caso, Ω es paralelo al eje norte o n, y:
- Ω Ω =⋅ ⋅ ()010),{displaystyle {boldsymbol ################################################################################################################################################################################################################################################################ }=omega {begin{pmatrix}01end{pmatrix}} v=()vevnvu),{displaystyle {boldsymbol {fn}={begin {pmatrix}v_{e}v_{n}g_{u}end{pmatrix}}}}} {}} {f}}}} {f}}}} {f}}}}} {f}}}}}}} {f}}}}}}}}}}} { aC=− − 2Ω Ω × × v=2⋅ ⋅ ()− − vu0ve).{displaystyle {boldsymbol {a}_{}=-2{boldsymbol {fnMinga times v}=2,omega ,{begin{pmatrix}-v_{u}v_{e}end{pmatrix}.}
En consecuencia, un movimiento hacia el este (es decir, en la misma dirección que la rotación de la esfera) proporciona una aceleración hacia arriba conocida como efecto Eötvös, y un movimiento hacia arriba produce una aceleración hacia el oeste.
Meteorología y oceanografía

Quizás el impacto más importante del efecto Coriolis está en la dinámica a gran escala de los océanos y la atmósfera. En meteorología y oceanografía, es conveniente postular un marco de referencia giratorio en el que la Tierra está estacionaria. En acomodación a esa postulación provisional, se introducen las fuerzas centrífuga y de Coriolis. Su importancia relativa está determinada por los números de Rossby aplicables. Los tornados tienen números de Rossby altos, por lo que, mientras que las fuerzas centrífugas asociadas con los tornados son bastante sustanciales, las fuerzas de Coriolis asociadas con los tornados son insignificantes a efectos prácticos.
Debido a que las corrientes oceánicas superficiales son impulsadas por el movimiento del viento sobre la superficie del agua, la fuerza de Coriolis también afecta el movimiento de las corrientes oceánicas y los ciclones. Muchas de las corrientes más grandes del océano circulan alrededor de áreas cálidas de alta presión llamadas giros. Aunque la circulación no es tan significativa como la del aire, la desviación causada por el efecto Coriolis es lo que crea el patrón en espiral en estos giros. El patrón de viento en espiral ayuda a que se forme el huracán. Cuanto más fuerte es la fuerza del efecto Coriolis, más rápido gira el viento y recoge energía adicional, lo que aumenta la fuerza del huracán.
El aire dentro de los sistemas de alta presión gira en una dirección tal que la fuerza de Coriolis se dirige radialmente hacia adentro y casi se equilibra con el gradiente de presión radial hacia afuera. Como resultado, el aire viaja en el sentido de las agujas del reloj alrededor de la alta presión en el hemisferio norte y en el sentido contrario a las agujas del reloj en el hemisferio sur. El aire alrededor de baja presión gira en la dirección opuesta, de modo que la fuerza de Coriolis se dirige radialmente hacia afuera y casi equilibra un gradiente de presión radial hacia adentro.
Flujo alrededor de un área de baja presión
Si se forma un área de baja presión en la atmósfera, el aire tiende a fluir hacia ella, pero la fuerza de Coriolis lo desvía perpendicularmente a su velocidad. Un sistema de equilibrio puede entonces establecerse creando un movimiento circular o un flujo ciclónico. Debido a que el número de Rossby es bajo, el equilibrio de fuerzas se encuentra en gran medida entre la fuerza del gradiente de presión que actúa hacia el área de baja presión y la fuerza de Coriolis que actúa alejándose del centro de la baja presión.
En lugar de fluir a favor del gradiente, los movimientos a gran escala en la atmósfera y el océano tienden a ocurrir en forma perpendicular al gradiente de presión. Esto se conoce como flujo geostrófico. En un planeta que no gira, el fluido fluiría a lo largo de la línea más recta posible, eliminando rápidamente los gradientes de presión. El equilibrio geostrófico es, por tanto, muy diferente del caso de los "movimientos de inercia" (ver más abajo), lo que explica por qué los ciclones de latitudes medias son más grandes en un orden de magnitud de lo que sería el flujo del círculo de inercia.
Este patrón de desviación y la dirección del movimiento se denomina ley de Buys-Ballot. En la atmósfera, el patrón de flujo se llama ciclón. En el hemisferio norte, la dirección del movimiento alrededor de un área de baja presión es en sentido contrario a las agujas del reloj. En el hemisferio sur, la dirección del movimiento es en el sentido de las agujas del reloj porque allí la dinámica de rotación es una imagen especular. A gran altura, el aire que se extiende hacia afuera gira en la dirección opuesta. Los ciclones rara vez se forman a lo largo del ecuador debido al débil efecto Coriolis presente en esta región.
Círculos de inercia
Una masa de aire o agua que se mueve con velocidad v{displaystyle v,} sujeto sólo a la fuerza Coriolis viaja en una trayectoria circular llamada una círculo inercial. Puesto que la fuerza se dirige a ángulos rectos al movimiento de la partícula, se mueve con una velocidad constante alrededor de un círculo cuyo radio R{displaystyle R. es dado por:
- R=vf{displaystyle R={frac {v} {f}}
Donde f{displaystyle f} es el parámetro Coriolis 2Ω Ω pecado φ φ {displaystyle 2Omega sin varphi }, presentado anteriormente (donde φ φ {displaystyle varphi } es la latitud). Por lo tanto, el tiempo necesario para que la masa complete un círculo completo es 2π π /f{displaystyle 2pi /f}. El parámetro Coriolis normalmente tiene un valor de media latitud de aproximadamente 10−4s−1; por lo tanto, para una velocidad atmosférica típica de 10 m/s (22 mph), el radio es de 100 km (62 mi) con un período de aproximadamente 17 horas. Para una corriente oceánica con una velocidad típica de 10 cm/s (0,22 mph), el radio de un círculo inercial es de 1 km (0,6 mi). Estos círculos inerciales son en sentido de reloj en el hemisferio norte (donde las trayectorias están dobladas a la derecha) y antiauricular en el hemisferio sur.
Si el sistema giratorio es un giratorio parabólico, entonces f{displaystyle f} es constante y las trayectorias son círculos exactos. En un planeta giratorio, f{displaystyle f} varía con latitud y los caminos de las partículas no forman círculos exactos. Desde el parámetro f{displaystyle f} varía como el seno de la latitud, el radio de las oscilaciones asociadas con una velocidad dada son más pequeños en los polos (latitud de ±90°), y aumentar hacia el ecuador.
Otros efectos terrestres
El efecto Coriolis afecta fuertemente la circulación oceánica y atmosférica a gran escala, lo que lleva a la formación de características sólidas como corrientes en chorro y corrientes fronterizas occidentales. Estas características están en equilibrio geostrófico, lo que significa que las fuerzas de Coriolis y gradiente de presión se equilibran entre sí. La aceleración de Coriolis también es responsable de la propagación de muchos tipos de ondas en el océano y la atmósfera, incluidas las ondas de Rossby y las ondas de Kelvin. También es fundamental en la llamada dinámica de Ekman en el océano y en el establecimiento del patrón de flujo oceánico a gran escala llamado equilibrio de Sverdrup.
Efecto Eötvös
El impacto práctico del "efecto Coriolis" es causado principalmente por el componente de aceleración horizontal producido por el movimiento horizontal.
Hay otros componentes del efecto Coriolis. Los objetos que viajan hacia el oeste se desvían hacia abajo, mientras que los objetos que viajan hacia el este se desvían hacia arriba. Esto se conoce como efecto Eötvös. Este aspecto del efecto Coriolis es mayor cerca del ecuador. La fuerza producida por el efecto Eötvös es similar a la componente horizontal, pero las fuerzas verticales mucho mayores debidas a la gravedad y la presión sugieren que no es importante en el equilibrio hidrostático. Sin embargo, en la atmósfera, los vientos están asociados con pequeñas desviaciones de presión del equilibrio hidrostático. En la atmósfera tropical, el orden de magnitud de las desviaciones de presión es tan pequeño que la contribución del efecto Eötvös a las desviaciones de presión es considerable.
Además, los objetos que viajan hacia arriba (es decir, afuera) o hacia abajo (es decir, adentro) se desvían hacia el oeste o el este, respectivamente. Este efecto también es mayor cerca del ecuador. Dado que el movimiento vertical suele ser de extensión y duración limitadas, el tamaño del efecto es más pequeño y requiere instrumentos precisos para detectarlo. Por ejemplo, los estudios de modelos numéricos idealizados sugieren que este efecto puede afectar directamente el campo de viento tropical a gran escala en aproximadamente un 10% dado el calentamiento o enfriamiento de larga duración (2 semanas o más) en la atmósfera. Además, en el caso de grandes cambios de impulso, como el lanzamiento de una nave espacial en órbita, el efecto se vuelve significativo. El camino a la órbita más rápido y más eficiente en combustible es un lanzamiento desde el ecuador que se curva hacia un rumbo directamente hacia el este.
Ejemplo intuitivo
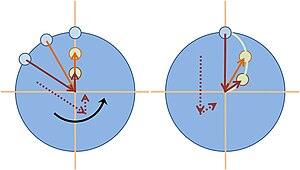
Imagina un tren que viaja a través de una línea ferroviaria sin fricción a lo largo del Ecuador. Supongamos que, cuando está en movimiento, se mueve a la velocidad necesaria para completar un viaje alrededor del mundo en un día (465 m/s). El efecto Coriolis se puede considerar en tres casos: cuando el tren viaja al oeste, cuando está en reposo, y cuando viaja al este. En cada caso, el efecto Coriolis se puede calcular desde el marco rotativo de referencia en la Tierra primero, y luego se comprueba contra un marco inercial fijo. La imagen de abajo ilustra los tres casos vistos por un observador en reposo en un (cerca) marco inercial desde un punto fijo sobre el Polo Norte a lo largo del eje de rotación de la Tierra; el tren es denotado por unos pocos píxeles rojos, fijos en el lado izquierdo en la imagen más izquierda, moviéndose en los otros ()1día=∧ ∧ 8s):{displaystyle left(1{text{ day}mathrel {overset {land }{=}} 8{text{ s}right):}
- El tren viaja hacia el oeste: En ese caso, se mueve contra la dirección de la rotación. Por lo tanto, en el marco giratorio de la Tierra el término Coriolis se apunta hacia el eje de rotación (abajo). Esta fuerza adicional hacia abajo debe hacer que el tren sea más pesado mientras se mueve en esa dirección.Si uno mira este tren desde el marco fijo de no rotación en la parte superior del centro de la Tierra, a esa velocidad permanece estacionario mientras la Tierra gira bajo ella. Por lo tanto, la única fuerza que actúa en ella es la gravedad y la reacción de la pista. Esta fuerza es mayor (en un 0,34%) que la fuerza que los pasajeros y el tren experimentan cuando descansan (en pie junto con la Tierra). Esta diferencia es lo que el efecto Coriolis representa en el marco rotativo de referencia.
- El tren llega a una parada: Desde el punto de vista del marco giratorio de la Tierra, la velocidad del tren es cero, por lo tanto la fuerza Coriolis es también cero y el tren y sus pasajeros recuperan su peso habitual.Desde el marco de referencia inercial fijo sobre la Tierra, el tren gira ahora junto con el resto de la Tierra. El 0,34% de la fuerza de gravedad proporciona la fuerza centrípeta necesaria para lograr el movimiento circular sobre ese marco de referencia. La fuerza restante, medida por una escala, hace que el tren y los pasajeros sean más ligeros que en el caso anterior.
- El tren viaja al este. En este caso, debido a que se mueve en la dirección del marco giratorio de la Tierra, el término Coriolis se dirige hacia fuera del eje de rotación (up). Esta fuerza ascendente hace que el tren parezca más ligero aún que cuando descansa.Desde el marco inercial fijo de referencia sobre la Tierra, el tren que viaja al este ahora gira al doble de la tasa que cuando estaba en reposo, por lo que la cantidad de fuerza centrípeta necesaria para causar que la ruta circular aumenta dejando menos fuerza de la gravedad para actuar en la pista. Esto es lo que el término Coriolis representa en el párrafo anterior.Como comprobación final se puede imaginar un marco de referencia girando junto con el tren. Tal marco estaría girando al doble de la velocidad angular que el marco giratorio de la Tierra. El componente de fuerza centrífuga resultante para ese marco imaginario sería mayor. Dado que el tren y sus pasajeros están en reposo, ese sería el único componente en ese marco explicando de nuevo por qué el tren y los pasajeros son más ligeros que en los dos casos anteriores.
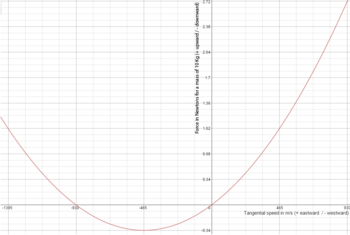 Gráfico de la fuerza experimentada por un objeto de 10 kilogramas (22 lb) como función de su velocidad que se mueve a lo largo del Ecuador de la Tierra (como se mide dentro del marco giratorio). (La fuerza positiva en el gráfico se dirige hacia arriba. La velocidad positiva se dirige hacia el este y la velocidad negativa se dirige hacia el oeste).
Gráfico de la fuerza experimentada por un objeto de 10 kilogramas (22 lb) como función de su velocidad que se mueve a lo largo del Ecuador de la Tierra (como se mide dentro del marco giratorio). (La fuerza positiva en el gráfico se dirige hacia arriba. La velocidad positiva se dirige hacia el este y la velocidad negativa se dirige hacia el oeste).
Esto también explica por qué los proyectiles de alta velocidad que viajan hacia el oeste se desvían hacia abajo y los que viajan hacia el este se desvían hacia arriba. Este componente vertical del efecto Coriolis se llama efecto Eötvös.
El ejemplo anterior se puede usar para explicar por qué el efecto Eötvös comienza a disminuir cuando un objeto viaja hacia el oeste a medida que su velocidad tangencial aumenta por encima de la rotación de la Tierra (465 m/s). Si el tren hacia el oeste en el ejemplo anterior aumenta la velocidad, parte de la fuerza de gravedad que empuja contra la vía representa la fuerza centrípeta necesaria para mantenerlo en movimiento circular en el marco de inercia. Una vez que el tren duplica su velocidad hacia el oeste a 930 m/s (2100 mph), esa fuerza centrípeta se vuelve igual a la fuerza que experimenta el tren cuando se detiene. Desde el marco inercial, en ambos casos gira a la misma velocidad pero en direcciones opuestas. Así, la fuerza es la misma anulando por completo el efecto Eötvös. Cualquier objeto que se mueva hacia el oeste a una velocidad superior a 930 m/s (2100 mph) experimenta una fuerza hacia arriba. En la figura, se ilustra el efecto Eötvös para un objeto de 10 kilogramos (22 lb) en el tren a diferentes velocidades. La forma parabólica se debe a que la fuerza centrípeta es proporcional al cuadrado de la velocidad tangencial. En el marco inercial, la parte inferior de la parábola está centrada en el origen. El desplazamiento se debe a que este argumento utiliza el marco de referencia giratorio de la Tierra. El gráfico muestra que el efecto Eötvös no es simétrico y que la fuerza hacia abajo resultante experimentada por un objeto que viaja hacia el oeste a alta velocidad es menor que la fuerza hacia arriba resultante cuando viaja hacia el este a la misma velocidad.
Drenajes en bañeras y aseos
Contrariamente al concepto erróneo popular, las bañeras, los inodoros y otros receptáculos de agua no se drenan en direcciones opuestas en los hemisferios norte y sur. Esto se debe a que la magnitud de la fuerza de Coriolis es despreciable a esta escala. Es probable que las fuerzas determinadas por las condiciones iniciales del agua (por ejemplo, la geometría del desagüe, la geometría del receptáculo, el impulso preexistente del agua, etc.) sean órdenes de magnitud mayores que la fuerza de Coriolis y, por lo tanto, determinarán la dirección de rotación del agua, si la hubiere. Por ejemplo, inodoros idénticos con descarga en ambos hemisferios drenan en la misma dirección, y esta dirección está determinada principalmente por la forma de la taza del inodoro.
En condiciones reales, la fuerza de Coriolis no influye de manera perceptible en la dirección del flujo de agua. Solo si el agua está tan quieta que la velocidad de rotación efectiva de la Tierra es más rápida que la del agua en relación con su contenedor, y si los pares aplicados externamente (como el que podría causar el flujo sobre una superficie de fondo irregular) son lo suficientemente pequeños, de hecho, el efecto de Coriolis puede determinar la dirección del vórtice. Sin una preparación tan cuidadosa, el efecto Coriolis será mucho menor que otras influencias en la dirección del drenaje, como cualquier rotación residual del agua y la geometría del recipiente.
Pruebas de laboratorio de agua de drenaje en condiciones atípicas
En 1962, Ascher Shapiro realizó un experimento en el MIT para probar la fuerza de Coriolis en un gran recipiente de agua, de 2 metros (6 pies 7 pulgadas) de ancho, con una pequeña cruz de madera sobre el orificio del tapón para mostrar la dirección de rotación., tapándolo y esperando al menos 24 horas para que el agua se asiente. En estas condiciones precisas de laboratorio, demostró el efecto y la rotación constante en sentido contrario a las agujas del reloj.
Informó que,
Ambas escuelas de pensamiento son en cierto sentido correctas. Para las observaciones cotidianas de la cocina fregadero y la variedad baño-tub, la dirección del vórtice parece variar de manera impredecible con la fecha, el tiempo del día, y el hogar particular del experimentador. Pero bajo condiciones de experimentación bien controladas, el observador mirando hacia abajo a un desagüe en el hemisferio norte siempre verá un vórtice contrarreloj, mientras que uno en el hemisferio sur siempre verá un vórtice de reloj. En un experimento diseñado correctamente, el vórtice es producido por las fuerzas de Coriolis, que son contrapuestas en el hemisferio norte.
Lloyd Trefethen informó sobre la rotación en el sentido de las agujas del reloj en el hemisferio sur en la Universidad de Sydney en cinco pruebas con tiempos de establecimiento de 18 h o más.
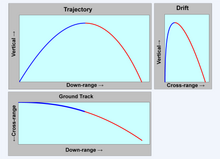
Trayectorias balísticas
La fuerza de Coriolis es importante en balística externa para calcular las trayectorias de proyectiles de artillería de muy largo alcance. El ejemplo histórico más famoso fue el cañón de París, utilizado por los alemanes durante la Primera Guerra Mundial para bombardear París desde una distancia de unos 120 km (75 mi). La fuerza de Coriolis cambia minuciosamente la trayectoria de una bala, lo que afecta la precisión a distancias extremadamente largas. Está ajustado por tiradores precisos de larga distancia, como francotiradores. En la latitud de Sacramento, California, un disparo de 910 m (1000 yardas) hacia el norte se desviaría 71 mm (2,8 pulgadas) hacia la derecha. También hay un componente vertical, explicado en la sección anterior del efecto Eötvös, que hace que los disparos hacia el oeste golpeen bajo y los disparos hacia el este golpeen alto.
Los efectos de la fuerza de Coriolis en las trayectorias balísticas no deben confundirse con la curvatura de las trayectorias de misiles, satélites y objetos similares cuando las trayectorias se trazan en mapas bidimensionales (planos), como la proyección de Mercator. Las proyecciones de la superficie curva tridimensional de la Tierra a una superficie bidimensional (el mapa) necesariamente da como resultado características distorsionadas. La aparente curvatura de la trayectoria es consecuencia de la esfericidad de la Tierra y ocurriría incluso en un marco no giratorio.
La fuerza de Coriolis sobre un proyectil en movimiento depende de los componentes de velocidad en las tres direcciones, la latitud y el azimut. Las direcciones suelen ser de rango descendente (la dirección a la que apunta inicialmente el arma), vertical y de rango cruzado.
- AX=− − 2⋅ ⋅ ()VY# Silencio Silencio latpecado φ φ az+VZpecado Silencio Silencio lat){displaystyle A_{mathrm {X} }=-2omega (V_{mathrm {Y}cos theta _{mathrm {lat} }sin phi _{mathrm {az} }+V_{mathrm {Z}sin theta _{mathrm {lat})}
- AY=2⋅ ⋅ ()VX# Silencio Silencio latpecado φ φ az+VZ# Silencio Silencio lat# φ φ az){displaystyle A_{mathrm {Y}=2omega (V_{mathrm {X}cos theta _{mathrm {lat} }sin phi _{mathrm {az} }+V_{mathrm {Z}cos theta _{mathrm {lat} }cos phi _{mathrm {az})}
- AZ=2⋅ ⋅ ()VXpecado Silencio Silencio lat− − VY# Silencio Silencio lat# φ φ az){displaystyle A_{mathrm {Z}=2omega (V_{mathrm {X}sin theta _{mathrm {lat} }-V_{mathrm {Y}cos theta _{mathrm {lat} }cos phi _{mathrm {az})}
dónde
- AX{displaystyle A_{mathrm {X}Aceleración de baja distancia.
- AY{displaystyle A_{mathrm}}, aceleración vertical con indicación positiva de aceleración hacia arriba.
- AZ{displaystyle A_{mathrm {Z}, aceleración transversal con indicación positiva de aceleración a la derecha.
- VX{displaystyle V_{mathrm {X}Velocidad baja.
- VY{displaystyle V_{mathrm {}}}, velocidad vertical con indicación positiva hacia arriba.
- VZ{displaystyle V_{mathrm {Z}, velocidad de rango cruzado con velocidad de indicación positiva a la derecha.
- ⋅ ⋅ {displaystyle omega } = 0.00007292 rad/sec, velocidad angular de la tierra (basada en un día sidereal).
- Silencio Silencio lat{displaystyle theta _{mathrm {lat}}, latitud con indicación positiva del hemisferio norte.
- φ φ az{displaystyle phi _{mathrm {az}}Azimuth midió el reloj del norte.
Visualización del efecto Coriolis
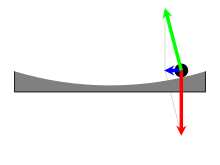
Para demostrar el efecto Coriolis, se puede utilizar un plato giratorio parabólico. En un plato giratorio plano, la inercia de un objeto co-rotatorio lo empuja hacia el borde. Sin embargo, si la superficie de la plataforma giratoria tiene la forma de paraboloide (tazón parabólico) correcta (vea la figura) y gira a la velocidad correspondiente, los componentes de fuerza que se muestran en la figura hacen que el componente de gravedad tangencial a la superficie del tazón sea exactamente igual a la fuerza centrípeta necesaria para mantener el objeto girando a su velocidad y radio de curvatura (suponiendo que no haya fricción). (Ver giro inclinado). Esta superficie cuidadosamente contorneada permite que la fuerza de Coriolis se muestre de forma aislada.
Los discos cortados de cilindros de hielo seco se pueden usar como discos, moviéndose casi sin fricción sobre la superficie de la plataforma giratoria parabólica, lo que permite que se muestren los efectos de Coriolis en los fenómenos dinámicos. Para obtener una vista de los movimientos vistos desde el marco de referencia que gira con la plataforma giratoria, se conecta una cámara de video a la plataforma giratoria para que co-rote con la plataforma giratoria, con los resultados que se muestran en la figura. En el panel izquierdo de la figura, que es el punto de vista de un observador estacionario, la fuerza gravitatoria en el marco de inercia que tira del objeto hacia el centro (parte inferior) del plato es proporcional a la distancia del objeto desde el centro. Una fuerza centrípeta de esta forma provoca el movimiento elíptico. En el panel de la derecha, que muestra el punto de vista del marco giratorio, la fuerza gravitatoria interna en el marco giratorio (la misma fuerza que en el marco inercial) se equilibra con la fuerza centrífuga externa (presente solo en el marco giratorio). Con estas dos fuerzas equilibradas, en el marco giratorio la única fuerza desequilibrada es Coriolis (también presente solo en el marco giratorio), y el movimiento es un círculo de inercia. El análisis y la observación del movimiento circular en el marco giratorio es una simplificación en comparación con el análisis y la observación del movimiento elíptico en el marco inercial.
Debido a que este marco de referencia gira varias veces por minuto en lugar de solo una vez al día como la Tierra, la aceleración de Coriolis producida es muchas veces mayor y, por lo tanto, más fácil de observar en escalas temporales y espaciales pequeñas que la aceleración de Coriolis causada por la rotación. de la tierra.
Por así decirlo, la Tierra es análoga a un plato giratorio de este tipo. La rotación ha provocado que el planeta se asiente en forma de esferoide, de modo que la fuerza normal, la fuerza gravitacional y la fuerza centrífuga se equilibran exactamente entre sí en un plano "horizontal" superficie. (Ver protuberancia ecuatorial).
El efecto Coriolis causado por la rotación de la Tierra se puede ver indirectamente a través del movimiento de un péndulo de Foucault.
Efectos de Coriolis en otras áreas
Caudalímetro Coriolis
Una aplicación práctica del efecto Coriolis es el medidor de flujo másico, un instrumento que mide la tasa de flujo másico y la densidad de un fluido que fluye a través de un tubo. El principio de funcionamiento consiste en inducir una vibración del tubo por el que pasa el fluido. La vibración, aunque no completamente circular, proporciona el marco de referencia giratorio que da lugar al efecto Coriolis. Si bien los métodos específicos varían según el diseño del medidor de flujo, los sensores monitorean y analizan los cambios en la frecuencia, el cambio de fase y la amplitud de los tubos de flujo vibrantes. Los cambios observados representan el caudal másico y la densidad del fluido.
Física molecular
En las moléculas poliatómicas, el movimiento de la molécula se puede describir mediante la rotación de un cuerpo rígido y la vibración interna de los átomos sobre su posición de equilibrio. Como resultado de las vibraciones de los átomos, los átomos están en movimiento en relación con el sistema de coordenadas de rotación de la molécula. Por lo tanto, los efectos de Coriolis están presentes y hacen que los átomos se muevan en una dirección perpendicular a las oscilaciones originales. Esto conduce a una mezcla de espectros moleculares entre los niveles de rotación y vibración, a partir de los cuales se pueden determinar las constantes de acoplamiento de Coriolis.
Precesión giroscópica
Cuando se aplica un par externo a un giroscopio giratorio a lo largo de un eje que está en ángulo recto con el eje de giro, la velocidad del borde que está asociada con el giro se dirige radialmente en relación con el eje de par externo. Esto hace que una fuerza inducida por par actúe sobre el borde de tal manera que incline el giroscopio en ángulo recto en la dirección en que lo habría inclinado el par externo. Esta tendencia tiene el efecto de mantener los cuerpos giratorios en su marco de rotación.
Vuelo de insectos
Las moscas (dípteros) y algunas polillas (lepidópteros) explotan el efecto Coriolis en vuelo con apéndices y órganos especializados que transmiten información sobre la velocidad angular de sus cuerpos.
Las fuerzas de Coriolis resultantes del movimiento lineal de estos apéndices se detectan dentro del marco de referencia giratorio de los insectos' cuerpos. En el caso de las moscas, sus apéndices especializados son órganos con forma de mancuerna ubicados justo detrás de sus alas llamados "halterios".
Los halterios de la mosca oscilan en un plano con la misma frecuencia de batido que las alas principales, de modo que cualquier rotación del cuerpo da como resultado una desviación lateral de los halterios de su plano de movimiento.
En las polillas, se sabe que sus antenas son responsables de la detección de las fuerzas de Coriolis de manera similar a los halterios de las moscas. Tanto en las moscas como en las polillas, una colección de mecanosensores en la base del apéndice es sensible a las desviaciones en la frecuencia de latido, en correlación con la rotación en los planos de cabeceo y balanceo, y al doble de la frecuencia de latido, en correlación con la rotación en el plano de guiñada.
Estabilidad del punto lagrangiano
En astronomía, los puntos de Lagrange son cinco posiciones en el plano orbital de dos cuerpos grandes en órbita donde un objeto pequeño afectado solo por la gravedad puede mantener una posición estable en relación con los dos cuerpos grandes. Los primeros tres puntos de Lagrange (L1, L2, L3) se encuentran a lo largo de la línea que conecta los dos cuerpos grandes, mientras que los dos últimos (L4 y L5) cada uno forma un triángulo equilátero con los dos cuerpos grandes. Los puntos L4 y L5, aunque corresponden a máximos del potencial efectivo en el marco de coordenadas que gira con los dos grandes cuerpos, son estables por el efecto de Coriolis. La estabilidad puede resultar en órbitas alrededor de L4 o L5, conocidas como órbitas de renacuajo, donde se pueden encontrar troyanos. También puede generar órbitas que rodeen L3, L4 y L5, conocidas como órbitas de herradura.
Contenido relacionado
Cantidad física
Proyecto manhattan
Onda triangular