Fuerza conservadora

format_list_bulleted Contenido keyboard_arrow_down

ImprimirCitar

La fuerza en la que el trabajo realizado para mover un objeto depende únicamente de su desplazamiento

En física, una fuerza conservativa es una fuerza con la propiedad de que el trabajo total realizado al mover una partícula entre dos puntos es independiente del camino seguido. De manera equivalente, si una partícula viaja en un circuito cerrado, el trabajo total realizado (la suma de la fuerza que actúa a lo largo del camino multiplicada por el desplazamiento) por una fuerza conservativa es cero.

Una fuerza conservativa depende únicamente de la posición del objeto. Si una fuerza es conservativa, es posible asignar un valor numérico al potencial en cualquier punto y, a la inversa, cuando un objeto se mueve de un lugar a otro, la fuerza cambia la energía potencial del objeto en una cantidad que no depende de el camino tomado, contribuyendo a la energía mecánica y la conservación general de la energía. Si la fuerza no es conservativa, entonces no es posible definir un potencial escalar, porque tomar caminos diferentes conduciría a diferencias de potencial conflictivas entre los puntos inicial y final.

La fuerza gravitatoria es un ejemplo de fuerza conservativa, mientras que la fuerza de fricción es un ejemplo de fuerza no conservativa.

Otros ejemplos de fuerzas conservativas son: fuerza en un resorte elástico, fuerza electrostática entre dos cargas eléctricas y fuerza magnética entre dos polos magnéticos. Las dos últimas fuerzas se denominan fuerzas centrales, ya que actúan a lo largo de la línea que une los centros de dos cuerpos cargados/magnetizados. Una fuerza central es conservativa si y sólo si es esféricamente simétrica.

Definición informal

Informalmente, una fuerza conservativa se puede considerar como una fuerza que conserva energía mecánica. Supongamos que una partícula comienza en el punto A y sobre ella actúa una fuerza F. Luego, la partícula es movida por otras fuerzas y eventualmente termina en A nuevamente. Aunque la partícula todavía puede estar moviéndose, en ese instante, cuando pasa de nuevo por el punto A, ha recorrido una trayectoria cerrada. Si el trabajo neto realizado por F en este punto es 0, entonces F pasa la prueba del camino cerrado. Cualquier fuerza que pase la prueba del camino cerrado para todos los caminos cerrados posibles se clasifica como una fuerza conservativa.

La fuerza gravitacional, la fuerza del resorte, la fuerza magnética (según algunas definiciones, ver más abajo) y la fuerza eléctrica (al menos en un campo magnético independiente del tiempo, ver la ley de inducción de Faraday para más detalles) son ejemplos de fuerzas conservativas, mientras que la fricción y la resistencia del aire son ejemplos clásicos de fuerzas no conservativas.

Para las fuerzas no conservativas, la energía mecánica que se pierde (no se conserva) tiene que ir a otro lugar, por conservación de la energía. Por lo general, la energía se convierte en calor, por ejemplo, el calor generado por la fricción. Además del calor, la fricción también suele producir algo de energía sonora. El arrastre del agua en un bote en movimiento convierte la energía mecánica del bote no solo en calor y energía sonora, sino también en energía de las olas en los bordes de su estela. Estas y otras pérdidas de energía son irreversibles debido a la segunda ley de la termodinámica.

Independencia de ruta

Una consecuencia directa de la prueba de trayectoria cerrada es que el trabajo realizado por una fuerza conservativa sobre una partícula que se mueve entre dos puntos cualesquiera no depende de la trayectoria seguida por la partícula.

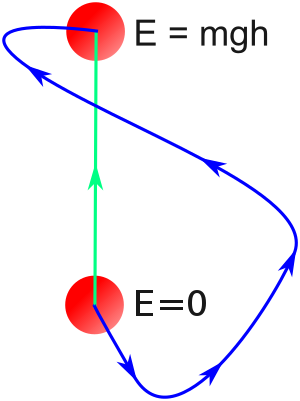
Esto se ilustra en la figura de la derecha: el trabajo realizado por la fuerza gravitatoria sobre un objeto depende únicamente de su cambio de altura porque la fuerza gravitacional es conservativa. El trabajo realizado por una fuerza conservativa es igual al negativo del cambio en la energía potencial durante ese proceso. Como prueba, imagine dos caminos 1 y 2, ambos yendo del punto A al punto B. La variación de energía para la partícula, tomando el camino 1 de A a B y luego el camino 2 hacia atrás de B a A, es 0; así, el trabajo es el mismo en el camino 1 y en el 2, es decir, el trabajo es independiente del camino seguido, siempre que vaya de A a B.

Por ejemplo, si un niño se desliza por un tobogán sin fricción, el trabajo realizado por la fuerza gravitacional sobre el niño desde el comienzo del tobogán hasta el final es independiente de la forma del tobogán; solo depende del desplazamiento vertical del niño.

Descripción matemática

Un campo de fuerza F, definido en todas partes en el espacio (o dentro de un volumen de espacio simplemente conectado), se denomina fuerza conservativa o campo vectorial conservativo si cumple alguna de estas tres condiciones equivalentes:

El rizo de F es el vector cero: ${displaystyle {vec {nabla }}times {vec {F}}={vec {0}}.}$ donde en dos dimensiones esto reduce a: ${displaystyle {frac {partial F_{y}}{partial x}}-{frac {partial F_{x}}{partial y}}=0}$
Hay cero trabajo neto (W) hecho por la fuerza al mover una partícula a través de una trayectoria que comienza y termina en el mismo lugar: ${displaystyle Wequiv oint _{C}{vec {F}}cdot mathrm {d} {vec {r}}=0.}$
La fuerza puede ser escrita como el gradiente negativo de un potencial, $Phi$ : ${displaystyle {vec {F}}=-{vec {nabla }}Phi.}$

Prueba de que estas tres condiciones son equivalentes cuando F es un campo de fuerza

1 implica 2: Vamos C ser cualquier camino cerrado simple (es decir, un camino que comienza y termina en el mismo punto y no tiene autointersecciones), y considerar una superficie S de los cuales C es el límite. Entonces el teorema de Stokes dice que ${displaystyle int _{S}left({vec {nabla }}times {vec {F}}right)cdot mathrm {d} {vec {a}}=oint _{C}{vec {F}}cdot mathrm {d} {vec {r}}}$ Si el rizo de F es cero el lado izquierdo es cero – por lo tanto la declaración 2 es verdad.
2 implica 3: Supongamos que la declaración 2 contiene. Vamos c ser una curva simple desde el origen hasta un punto $x$ y definir una función ${displaystyle Phi (x)=-int _{c}{vec {F}}cdot mathrm {d} {vec {r}}.}$ El hecho de que esta función sea bien definida (independiente de la elección de c) A continuación de la declaración 2. De todos modos, del teorema fundamental del cálculo, sigue que ${displaystyle {vec {F}}=-{vec {nabla }}Phi.}$ Así pues, la declaración 2 implica la declaración 3 (véase la prueba completa).
3 implica 1: Por último, asuma que la tercera declaración es verdadera. Una conocida identidad de cálculo vectorial declara que el rizo del gradiente de cualquier función es 0. (Ver la prueba.) Por lo tanto, si la tercera declaración es verdadera, entonces la primera declaración debe ser verdadera también. Esto demuestra que la declaración 1 implica 2, 2 implica 3, y 3 implica 1. Por lo tanto, los tres son equivalentes, Q.E.D. (La equivalencia de 1 y 3 también se conoce como (un aspecto de) Teorema de Helmholtz.)

El término fuerza conservativa proviene del hecho de que cuando existe una fuerza conservativa, conserva la energía mecánica. Las fuerzas conservativas más conocidas son la gravedad, la fuerza eléctrica (en un campo magnético independiente del tiempo, véase la ley de Faraday) y la fuerza del resorte.

Muchas fuerzas (particularmente aquellas que dependen de la velocidad) no son campos de fuerza. En estos casos, las tres condiciones anteriores no son matemáticamente equivalentes. Por ejemplo, la fuerza magnética satisface la condición 2 (dado que el trabajo realizado por un campo magnético sobre una partícula cargada siempre es cero), pero no satisface la condición 3, y la condición 1 ni siquiera está definida (la fuerza no es un campo vectorial, por lo que no se puede evaluar su curvatura). En consecuencia, algunos autores clasifican la fuerza magnética como conservativa, mientras que otros no. La fuerza magnética es un caso inusual; la mayoría de las fuerzas dependientes de la velocidad, como la fricción, no satisfacen ninguna de las tres condiciones y, por lo tanto, son inequívocamente no conservativas.

Fuerza no conservativa

A pesar de la conservación de la energía total, pueden surgir fuerzas no conservativas en la física clásica debido a grados de libertad despreciados oa potenciales dependientes del tiempo. Muchas fuerzas no conservativas pueden percibirse como efectos macroscópicos de fuerzas conservativas a pequeña escala. Por ejemplo, la fricción puede tratarse sin violar la conservación de la energía considerando el movimiento de moléculas individuales; sin embargo, eso significa que se debe considerar el movimiento de cada molécula en lugar de manejarlo a través de métodos estadísticos. Para los sistemas macroscópicos, la aproximación no conservativa es mucho más fácil de manejar que los millones de grados de libertad.

Ejemplos de fuerzas no conservativas son la fricción y la tensión de materiales no elásticos. La fricción tiene el efecto de transferir parte de la energía del movimiento a gran escala de los cuerpos a movimientos a pequeña escala en su interior y, por lo tanto, parece no conservativo a gran escala. La relatividad general no es conservativa, como se ve en la precesión anómala de la órbita de Mercurio. Sin embargo, la relatividad general conserva un pseudotensor de tensión-energía-momento.

Contenido relacionado

Más resultados...