Frecuencia (estadísticas)
En las estadísticas, frecuencia o frecuencia absoluta de un evento es el número de veces la observación se ha producido/recordado en un experimento o estudio. Estas frecuencias se representan gráficamente o en forma tabular.
Tipos
La frecuencia acumulada es la suma de las frecuencias absolutas de todos los eventos en un punto determinado o por debajo de él en una lista ordenada de eventos.
La frecuencia relativa (o probabilidad empírica) de un evento es la frecuencia absoluta normalizada por el número total de eventos:
Los valores de para todos los eventos se puede trazar para producir una distribución de frecuencias.
En el caso cuando para ciertos , se pueden añadir pseudocuentos.
Depicting frequency distributions
Una distribución de frecuencia muestra una agrupación resumida de datos divididos en clases mutuamente excluyentes y el número de ocurrencias en una clase. Es una forma de mostrar datos no organizados, en particular para mostrar los resultados de una elección, los ingresos de las personas en una región determinada, las ventas de un producto en un período determinado, los montos de los préstamos estudiantiles de los graduados, etc. Algunos de los gráficos que se pueden utilizar con distribuciones de frecuencia son histogramas, gráficos de líneas, gráficos de barras y gráficos circulares. Las distribuciones de frecuencia se utilizan tanto para datos cualitativos como cuantitativos.
Construcción
- Decide el número de clases. Demasiadas clases o muy pocas clases podrían no revelar la forma básica del conjunto de datos, también será difícil interpretar dicha distribución de frecuencia. El número ideal de clases puede ser determinado o estimado por fórmula: (regla base 10), o por la fórmula de elección cuadrada Donde n es el número total de observaciones en los datos. (Este último será demasiado grande para grandes conjuntos de datos como estadísticas de población.) Sin embargo, estas fórmulas no son una regla difícil y el número resultante de clases determinadas por fórmula puede no ser siempre exactamente adecuado con los datos que se tratan.
- Calcular el rango de los datos (Range = Max – Min) encontrando los valores mínimos y máximos de datos. El rango se utilizará para determinar el intervalo de clase o el ancho de clase.
- Decide el ancho de las clases, denotado por h y obtenido por (asumiendo que los intervalos de clase son los mismos para todas las clases).
En general, el intervalo de clase o el ancho de clase es el mismo para todas las clases. Las clases en conjunto deben cubrir al menos la distancia desde el valor más bajo (mínimo) en los datos hasta el valor más alto (máximo). Los intervalos de clase iguales son los preferidos en la distribución de frecuencias, mientras que los intervalos de clase desiguales (por ejemplo, intervalos logarítmicos) pueden ser necesarios en ciertas situaciones para producir una buena dispersión de observaciones entre las clases y evitar una gran cantidad de clases vacías o casi vacías.
- Decidir los límites de clase individuales y seleccionar un punto de partida adecuado de la primera clase que es arbitraria; puede ser inferior o igual al valor mínimo. Normalmente se inicia antes del valor mínimo de tal manera que el punto medio (el promedio de los límites de clase inferior y superior de la primera clase) se coloca correctamente.
- Tome una observación y marque una barra vertical (última) para una clase que pertenece. Se mantiene una historia de ejecución hasta la última observación.
- Encuentra las frecuencias, frecuencia relativa, frecuencia acumulativa, etc. según sea necesario.
Los siguientes son algunos métodos comúnmente utilizados para representar la frecuencia:
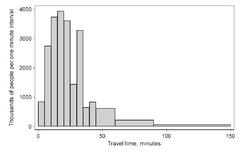
Histogramas
Un histograma es una representación de frecuencias tabuladas, que se muestra como rectángulos o cuadrados adyacentes (en algunas situaciones), erigidos sobre intervalos discretos (contenedores), con un área proporcional a la frecuencia de las observaciones en el intervalo. La altura de un rectángulo también es igual a la densidad de frecuencia del intervalo, es decir, la frecuencia dividida por el ancho del intervalo. El área total del histograma es igual a la cantidad de datos. Un histograma también se puede normalizar mostrando frecuencias relativas. Luego muestra la proporción de casos que caen en cada una de varias categorías, con un área total igual a 1. Las categorías generalmente se especifican como intervalos consecutivos, no superpuestos de una variable. Las categorías (intervalos) deben ser adyacentes y, a menudo, se eligen para que tengan el mismo tamaño. Los rectángulos de un histograma se dibujan de manera que se toquen entre sí para indicar que la variable original es continua.
Gráficos de bar
Un gráfico de barras es un gráfico con barras rectangulares cuya longitud es proporcional a los valores que representan. Las barras se pueden trazar vertical u horizontalmente. Un gráfico de barras verticales a veces se denomina gráfico de barras de columnas.
Cuadro de distribución de frecuencias
Una tabla de distribución de frecuencias es una disposición de los valores que una o más variables toman en una muestra. Cada entrada de la tabla contiene la frecuencia o el recuento de ocurrencias de valores dentro de un grupo o intervalo en particular y, de esta manera, la tabla resume la distribución de valores en la muestra.
Este es un ejemplo de una tabla de frecuencias univariada (=variable única). Se muestra la frecuencia de cada respuesta a una pregunta de una encuesta.
| Rank | Grado de acuerdo | Número |
|---|---|---|
| 1 | Estoy de acuerdo. | 22 |
| 2 | De acuerdo. | 30 |
| 3 | No estoy seguro | 20 |
| 4 | Disacuerdo un poco | 15 |
| 5 | No está de acuerdo. | 15 |
Un esquema de tabulación diferente agrega valores en grupos de modo que cada grupo abarque un rango de valores. Por ejemplo, las alturas de los estudiantes de una clase podrían organizarse en la siguiente tabla de frecuencias.
| Rango de altura | Número de estudiantes | Número acumulado |
|---|---|---|
| menos de 5 metros | 25 | 25 |
| 5,5 pies | 35 | 60 |
| 5,5 a 36 pies | 20 | 80 |
| 6,0 a 6,5 pies | 20 | 100 |
Distribución conjunta de frecuencias
Las distribuciones de frecuencia conjuntas bivariadas se presentan a menudo como tablas de contingencia (de dos vías):
| Baile | Deportes | TV | Total | |
|---|---|---|---|---|
| Hombres | 2 | 10 | 8 | 20 |
| Mujeres | 16 | 6 | 8 | 30 |
| Total | 18 | 16 | 16 | 50 |
La fila total y la columna total informan las frecuencias marginales o la distribución marginal, mientras que el cuerpo de la tabla informa las frecuencias conjuntas.
Interpretación
Según la interpretación de la probabilidad en términos de frecuencia, se supone que a medida que la duración de una serie de ensayos aumenta sin límite, la fracción de experimentos en los que ocurre un evento determinado se acercará a un valor fijo, conocido como la frecuencia relativa límite.
Esta interpretación se contrasta a menudo con la probabilidad bayesiana. De hecho, el término "frecuentista" fue utilizado por primera vez por M. G. Kendall en 1949, para contrastarlo con los bayesianos, a quienes llamó "no frecuentistas". Observó que
- 3.... podemos distinguir ampliamente dos actitudes principales. Uno toma la probabilidad como 'un grado de creencia racional', o alguna idea similar...el segundo define la probabilidad en términos de frecuencias de ocurrencia de eventos, o por proporciones relativas en 'poblaciones' o 'colectivas'; (pág. 101)
- ...
- 12. Se podría pensar que las diferencias entre los frecuentados y los no-frecuentes (si puedo llamarlos así) se deben en gran medida a las diferencias de los dominios que pretenden cubrir. (pág. 104)
- ...
- Afirmo que esto no es así... La distinción esencial entre los frecuentados y los no-frecuentes es, creo, que el primero, en un esfuerzo por evitar cualquier cosa que favorezca asuntos de opinión, busca definir la probabilidad en términos de las propiedades objetivas de una población, real o hipotética, mientras que este último no lo hace. [emfasis en original]
Aplicaciones
La gestión y el trabajo con datos tabulados de frecuencia es mucho más sencillo que el trabajo con datos sin procesar. Existen algoritmos simples para calcular la mediana, la media, la desviación estándar, etc. a partir de estas tablas.
La prueba de hipótesis estadística se basa en la evaluación de las diferencias y similitudes entre distribuciones de frecuencias. Esta evaluación implica medidas de tendencia central o promedios, como la media y la mediana, y medidas de variabilidad o dispersión estadística, como la desviación estándar o la varianza.
Se dice que una distribución de frecuencias está sesgada cuando su media y mediana son significativamente diferentes, o de manera más general, cuando es asimétrica. La curtosis de una distribución de frecuencias es una medida de la proporción de valores extremos (valores atípicos) que aparecen en cada extremo del histograma. Si la distribución es más propensa a valores atípicos que la distribución normal, se dice que es leptocúrtica; si es menos propensa a valores atípicos, se dice que es platicúrtica.
Las distribuciones de frecuencia de letras también se utilizan en el análisis de frecuencia para descifrar códigos y se utilizan para comparar las frecuencias relativas de las letras en diferentes idiomas. A menudo se utilizan otros idiomas, como el griego, el latín, etc.
Véase también
- Frecuencia aperódica
- Cuenta datos
- tabulación cruzada
- Función de distribución acumulativa
- Análisis de frecuencia acumulativa
- Función de distribución empírica
- Ley de grandes cantidades
- Multiset multiplicidad como analógico de frecuencia
- Función de densidad de probabilidad
- Interpretaciones de probabilidad
- Regularidad estadística
- Frecuencia de palabras
Referencias
- ^ a b Kenney, J. F.; Keeping, E. S. (1962). Matemáticas de Estadísticas, Parte 1 (3a edición). Princeton, NJ: Van Nostrand Reinhold.
- ^ Manikandan, S (1 de enero de 2011). "Distribución de frecuencias". Journal of Pharmacology " Pharmacotherapeutics. 2 (1): 54-55. doi:10.4103/0976-500X.77120. ISSN 0976-500X. PMC 3117575. PMID 21701652.
- ^ Carlson, K. and Winquist, J. (2014) Introducción a las estadísticas. SAGE Publications, Inc. Capítulo 1: Introducción a las distribuciones de estadísticas y frecuencias
- ^ Howitt, D. and Cramer, D. (2008) Estadísticas en Psicología. Prentice Hall
- ^ Charles Stangor (2011) "Metodos de investigación para las ciencias conductuales". Wadsworth, Cengage Learning. ISBN 9780840031976.
- ^ Stat Trek, Statistics and Probability Glosary, s.v. Frecuencia conjunta
- ^ von Mises, Richard (1939) Probabilidad, estadísticas y verdad (en alemán) (traducción en inglés, 1981: Dover Publications; 2 Revised edition. ISBN 0486242145) (p.14)
- ^ La teoría de la frecuencia Capítulo 5; discutido en Donald Gilles, Teorías filosóficas de probabilidad (2000), Psychology Press. ISBN 9780415182751 pág. 88.
- ^ Usos más conocidos de algunas de las palabras de probabilidad " Estadísticas
- ^ Kendall, Maurice George (1949). "Sobre la reconciliación de las teorías de la probabilidad". Biometrika. 36 (1/2). Biometrika Trust: 101–116. doi:10.1093/biomet/36.1-2.101. JSTOR 2332534.