Fractura

format_list_bulleted Contenido keyboard_arrow_down

ImprimirCitar

Separación de materiales o estructuras bajo estrés

Fallo dúctil de un espécimen metálico colado axialmente

v t e Modos mecánicos de falla
Buckling Corrosión fatiga por corrosión Creep Fatiga Fouling Fracturas Hidrogen embrittlement Impacto Embrittle de metal líquido Sobrecarga mecánica Embrittlement inducido por metal Estrés corrosión cracking Sulfide stress cracking shock térmico Wear Rendimiento

Fractura es la separación de un objeto o material en dos o más piezas bajo la acción de una tensión. La fractura de un sólido generalmente ocurre debido al desarrollo de ciertas superficies de discontinuidad de desplazamiento dentro del sólido. Si se desarrolla un desplazamiento perpendicular a la superficie, se denomina fisura de tracción normal o simplemente fisura; si un desplazamiento se desarrolla tangencialmente, se denomina grieta de corte, banda de deslizamiento o dislocación.

Las fracturas frágiles ocurren sin ninguna deformación aparente antes de la fractura. Las fracturas dúctiles ocurren después de una deformación visible. La resistencia a la fractura, o resistencia a la rotura, es la tensión cuando una muestra falla o se fractura. La comprensión detallada de cómo se produce y se desarrolla una fractura en los materiales es el objeto de la mecánica de la fractura.

Fuerza

Curva de tensión vs. típica de aluminio

Última fuerza de tracción
Fuerza de rendimiento
Tensión límite proporcional
Fracturas
Tensión Offset (típicamente 0,2%)

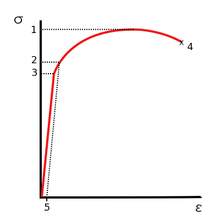
La resistencia a la fractura, también conocida como resistencia a la rotura, es la tensión a la que falla una muestra por fractura. Esto generalmente se determina para un espécimen determinado mediante una prueba de tracción, que traza la curva de tensión-deformación (ver imagen). El último punto registrado es la resistencia a la fractura.

Los materiales dúctiles tienen una resistencia a la fractura inferior a la resistencia máxima a la tracción (UTS), mientras que en los materiales frágiles la resistencia a la fractura es equivalente a la UTS. Si un material dúctil alcanza su máxima resistencia a la tracción en una situación de carga controlada, continuará deformándose, sin aplicación de carga adicional, hasta que se rompa. Sin embargo, si la carga está controlada por desplazamiento, la deformación del material puede aliviar la carga, evitando la ruptura.

Las estadísticas de fractura en materiales aleatorios tienen un comportamiento muy intrigante, y los arquitectos e ingenieros lo observaron muy pronto. De hecho, los estudios de fracturas o rupturas podrían ser los estudios de ciencias físicas más antiguos, que aún siguen siendo intrigantes y muy vivos. Leonardo da Vinci, hace más de 500 años, observó que las resistencias a la tracción de especímenes nominalmente idénticos de alambre de hierro disminuyen al aumentar la longitud de los alambres (ver, por ejemplo, una discusión reciente). Galileo Galilei hizo observaciones similares hace más de 400 años. Esta es la manifestación de las estadísticas extremas de falla (un volumen de muestra más grande puede tener defectos más grandes debido a las fluctuaciones acumulativas donde las fallas se nuclean e inducen una menor resistencia de la muestra).

Tipos

Hay dos tipos de fracturas: fracturas frágiles y dúctiles, respectivamente, sin o con deformación plástica antes de la falla.

Frágil

Fractura frágil en vidrio

Fracture de un brazo de manivela de aluminio de una bicicleta, donde las áreas brillantes muestran una fractura frágil, y las áreas oscuras muestran fractura de fatiga.

En la fractura frágil, no se produce deformación plástica aparente antes de la fractura. La fractura frágil generalmente implica poca absorción de energía y ocurre a altas velocidades, hasta 2133,6 m/s (7000 pies/s) en acero. En la mayoría de los casos, la fractura frágil continuará incluso cuando se interrumpa la carga.

En materiales cristalinos quebradizos, la fractura puede ocurrir por escisión como resultado de la tensión de tracción que actúa normal a los planos cristalográficos con baja adherencia (planos de escisión). En los sólidos amorfos, por el contrario, la falta de una estructura cristalina da como resultado una fractura concoidea, con grietas que proceden normales a la tensión aplicada.

La resistencia a la fractura (o tensión de nucleación de microfisuras) de un material fue estimada teóricamente por primera vez por Alan Arnold Griffith en 1921:

sigma _{{mathrm {theoretical}}}={sqrt {{frac {Egamma }{r_{o}}}}}

donde: –

Superficie de fractura de cuello de botella de un microscopio electrónico de escaneo

E

es el módulo de Young del material,

gamma

es la energía superficial, y

r_{o}

es la longitud micro-crack (o distancia de equilibrio entre los centros atómicos en un sólido cristalino).

Por otro lado, una fisura introduce una concentración de tensión modelada por la ecuación de Inglis

sigma _{{mathrm {elliptical crack}}}=sigma _{{mathrm {applied}}}left(1+2{sqrt {{frac {a}{rho }}}}right)=2sigma _{{mathrm {applied}}}{sqrt {{frac {a}{rho }}}}

(Por grietas agudas)

donde: –

sigma _{{mathrm {applied}}}

es el estrés de carga,

a

es la mitad de la longitud de la grieta, y

rho

es el radio de curvatura en la punta de la grieta.

Juntando estas dos ecuaciones se obtiene

sigma _{{mathrm {fracture}}}={sqrt {{frac {Egamma rho }{4ar_{o}}}}}.

grietas afiladas (pequeñas $rho$ ) y grandes defectos (grandes $a$ ) ambos bajan la fuerza de la fractura del material.

Recientemente, los científicos han descubierto la fractura supersónica, el fenómeno de propagación de grietas más rápido que la velocidad del sonido en un material. Este fenómeno también se verificó recientemente mediante experimentos de fractura en materiales similares al caucho.

La secuencia básica en una fractura frágil típica es: introducción de una falla ya sea antes o después de que el material se ponga en servicio, propagación lenta y estable de grietas bajo cargas recurrentes y falla repentina y rápida cuando la grieta alcanza una longitud de grieta crítica según las condiciones definidas por la mecánica de la fractura. La fractura frágil se puede evitar controlando tres factores principales: la tenacidad a la fractura del material (K_c), el nivel de tensión nominal (σ) y el tamaño del defecto introducido (a). Las tensiones residuales, la temperatura, la tasa de carga y las concentraciones de tensión también contribuyen a la fractura frágil al influir en los tres factores principales.

Bajo ciertas condiciones, los materiales dúctiles pueden mostrar un comportamiento frágil. Las condiciones de carga rápida, baja temperatura y tensión triaxial pueden hacer que los materiales dúctiles fallen sin deformación previa.

Dúctil

Representación esquemática de los pasos en fractura dúctil (en tensión pura)

En la fractura dúctil, se produce una extensa deformación plástica (estricción) antes de la fractura. Los términos "ruptura" y "rotura dúctil" describir la falla final de materiales dúctiles cargados en tensión. La gran plasticidad hace que la grieta se propague lentamente debido a la absorción de una gran cantidad de energía antes de la fractura.

Superficie de fractura dúctil de aluminio 6061-T6

Debido a que la ruptura dúctil implica un alto grado de deformación plástica, el comportamiento de fractura de una grieta que se propaga como se modeló anteriormente cambia fundamentalmente. Parte de la energía de las concentraciones de tensión en las puntas de las grietas se disipa por deformación plástica delante de la grieta a medida que se propaga.

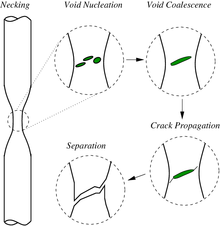
Los pasos básicos en la fractura dúctil son la formación de microvacíos, la coalescencia de microvacíos (también conocida como formación de grietas), la propagación de grietas y la falla, lo que a menudo resulta en una superficie de falla en forma de copa y cono. Los microhuecos se nuclean en varias discontinuidades internas, como precipitados, fases secundarias, inclusiones y límites de grano en el material. A medida que aumenta la tensión local, los microhuecos crecen, se unen y finalmente forman una superficie de fractura continua. La fractura dúctil es típicamente transgranular y la deformación debido al deslizamiento de la dislocación puede causar el labio de corte característico de la fractura de copa y cono.

La coalescencia de los microhuecos da como resultado una apariencia de hoyuelos en la superficie de la fractura. La forma del hoyuelo está fuertemente influenciada por el tipo de carga. La fractura bajo una carga de tracción uniaxial local generalmente da como resultado la formación de hoyuelos equiaxiales. Las fallas causadas por cortante producirán hoyuelos alargados o de forma parabólica que apuntan en direcciones opuestas en las superficies de fractura coincidentes. Finalmente, el desgarro por tracción produce hoyuelos alargados que apuntan en la misma dirección en las superficies de fractura coincidentes.

Características

La forma en que una grieta se propaga a través de un material da una idea del modo de fractura. Con la fractura dúctil, una grieta se mueve lentamente y se acompaña de una gran cantidad de deformación plástica alrededor de la punta de la grieta. Una fisura dúctil normalmente no se propagará a menos que se aplique un mayor esfuerzo y, por lo general, dejará de propagarse cuando se elimine la carga. En un material dúctil, una fisura puede progresar a una sección del material donde las tensiones son ligeramente inferiores y detenerse debido al efecto de reducción de las deformaciones plásticas en la punta de la fisura. Por otro lado, con fractura frágil, las grietas se propagan muy rápidamente con poca o ninguna deformación plástica. Las grietas que se propagan en un material quebradizo seguirán creciendo una vez iniciadas.

La propagación de grietas también se clasifica por las características de grietas a nivel microscópico. Una grieta que atraviesa los granos dentro del material sufre una fractura transgranular. Una grieta que se propaga a lo largo de los límites de grano se denomina fractura intergranular. Normalmente, los enlaces entre los granos del material son más fuertes a temperatura ambiente que el propio material, por lo que es más probable que se produzca una fractura transgranular. Cuando las temperaturas aumentan lo suficiente como para debilitar los enlaces de los granos, la fractura intergranular es el modo de fractura más común.

Pruebas

La fractura en materiales se estudia y cuantifica de múltiples maneras. La fractura se determina en gran medida por la dureza de la fractura ( ${textstyle mathrm {K} _{mathrm {c} }}$ ), así que las pruebas de fractura se hacen a menudo para determinar esto. Las dos técnicas más utilizadas para determinar la dureza de fractura son la prueba flexural de tres puntos y la prueba compacta de tensión.

Al realizar las pruebas de tracción compacta y flexión de tres puntos, se puede determinar la tenacidad a la fractura a través de la siguiente ecuación:

{displaystyle mathrm {K_{c}} =sigma _{mathrm {F} }{sqrt {pi mathrm {c} }}mathrm {f (c/a)} }

Dónde:-

{displaystyle mathrm {f (c/a)} }

es una ecuación empíricamente derivada para capturar la geometría de la muestra de prueba

{displaystyle sigma _{mathrm {F} }}

es el estrés de la fractura, y

{displaystyle mathrm {c} }

es la longitud de la grieta.

Para alcanzar con precisión ${textstyle mathrm {K} _{mathrm {c} }}$ , el valor de ${textstyle mathrm {c} }$ debe medirse con precisión. Esto se hace tomando la pieza de prueba con su muesca fabricada de longitud ${textstyle mathrm {cprime } }$ y afilar esta muesca para emular mejor una punta de crack encontrada en materiales del mundo real. La prestrecha cíclica de la muestra puede entonces inducir una grieta de fatiga que extiende la grieta de la longitud de ganga fabricada ${textstyle mathrm {cprime } }$ a ${textstyle mathrm {c} }$ . Este valor ${textstyle mathrm {c} }$ se utiliza en las ecuaciones anteriores para determinar ${textstyle mathrm {K} _{mathrm {c} }}$ .

Después de esta prueba, la muestra puede ser reordenada de tal manera que la carga adicional de una carga (F) extenderá esta grieta y así se puede obtener una curva de carga versus deflexión de muestra. Con esta curva, se puede obtener la pendiente de la porción lineal, que es la inversa del cumplimiento del material. Esto se utiliza para derivar f(c/a) como se define anteriormente en la ecuación. Con el conocimiento de todas estas variables, ${textstyle mathrm {K} _{mathrm {c} }}$ entonces se puede calcular.

Cerámicas y vidrios inorgánicos

Las cerámicas y las gafas inorgánicas tienen comportamientos de fractura que difieren de los materiales metálicos. Las cerámicas tienen altas resistencias y realizan bien en altas temperaturas debido a la fuerza material siendo independiente de la temperatura. Las cerámicas tienen baja dureza determinada por las pruebas bajo una carga de tracción; a menudo, las cerámicas tienen ${textstyle mathrm {K} _{mathrm {c} }}$ valores que son ~5% de los que se encuentran en metales. Sin embargo, como lo demuestran Faber y Evans, la dureza de las fracturas se puede predecir y mejorar con la deflexión del crack alrededor de partículas de segunda fase. Las cerámicas generalmente se cargan en compresión en uso cotidiano, por lo que la fuerza compresiva se conoce a menudo como la fuerza; esta fuerza a menudo puede exceder la de la mayoría de los metales. Sin embargo, la cerámica es frágil y por lo tanto la mayor parte del trabajo gira en torno a la prevención de la fractura frágil. Debido a cómo se fabrican y procesan cerámicas, a menudo hay defectos preexistentes en el material introducir un alto grado de variabilidad en la fractura de hervidor Mode I. Por lo tanto, hay una naturaleza probabilística que se debe contabilizar en el diseño de la cerámica. La distribución Weibull predice la probabilidad de supervivencia de una fracción de muestras con un cierto volumen que sobrevive un sigma de estrés tensil, y a menudo se utiliza para evaluar mejor el éxito de una cerámica para evitar fracturas.

Haces de fibras

Para modelar la fractura de un haz de fibras, Thomas Pierce introdujo el Modelo de haz de fibras en 1926 como un modelo para comprender la resistencia de los materiales compuestos. El paquete consta de un gran número de resortes Hookean paralelos de longitud idéntica y cada uno con constantes de resorte idénticas. Sin embargo, tienen diferentes tensiones de rotura. Todos estos resortes están suspendidos de una plataforma horizontal rígida. La carga está unida a una plataforma horizontal, conectada a los extremos inferiores de los resortes. Cuando esta plataforma inferior es absolutamente rígida, la carga en cualquier punto del tiempo se comparte por igual (independientemente de cuántas fibras o resortes se hayan roto y dónde) entre todas las fibras supervivientes. Este modo de carga compartida se denomina modo de carga compartida equitativa. También se puede suponer que la plataforma inferior tiene una rigidez finita, por lo que la deformación local de la plataforma se produce cuando fallan los resortes y las fibras vecinas supervivientes tienen que compartir una fracción mayor de la transferida desde la fibra que ha fallado. El caso extremo es el del modelo de distribución de carga local, donde la carga del resorte o la fibra que falla se comparte (generalmente por igual) con las fibras vecinas más cercanas supervivientes.

Desastres

Las fallas causadas por la fractura frágil no se han limitado a ninguna categoría particular de estructura de ingeniería. Aunque la fractura frágil es menos común que otros tipos de fallas, los impactos sobre la vida y la propiedad pueden ser más severos. Las siguientes fallas históricas notables se atribuyeron a la fractura frágil:

Barcos de presión: Gran flujo de mosaicos en 1919, Nueva Jersey falla de tanques en 1973
Puentes: King Street Bridge se colapsó en 1962, Silver Bridge colapsó en 1967, falla parcial del puente Hoan en 2000
Naves: Titanic en 1912, Liberty barcos durante la Segunda Guerra Mundial, SS Schenectady en 1943

Mecánica de Fractura Computacional

Prácticamente todas las áreas de la ingeniería se han visto afectadas significativamente por las computadoras, y la mecánica de fracturas no es una excepción. Dado que existen tan pocos problemas reales con soluciones analíticas de forma cerrada, el modelado numérico se ha convertido en una herramienta esencial en el análisis de fracturas. Hay literalmente cientos de configuraciones para las que se han publicado soluciones de intensidad de tensión, la mayoría de las cuales se derivaron de modelos numéricos. Los cálculos de la integral J y el desplazamiento de la apertura de la punta de la grieta (CTOD) son dos estudios elástico-plásticos cada vez más populares. Además, los expertos están utilizando herramientas computacionales de vanguardia para estudiar problemas únicos como la propagación de grietas dúctiles, la fractura dinámica y la fractura en las interfaces. El aumento exponencial de las aplicaciones de la mecánica de fractura computacional es esencialmente el resultado de los rápidos avances en la tecnología informática.

Los métodos numéricos computacionales más utilizados son los métodos de elementos finitos y ecuaciones integrales de contorno. Otros métodos incluyen la coincidencia de tensión y desplazamiento, avance de grietas de elementos, en los que los dos últimos se incluyen en Métodos tradicionales en mecánica computacional de fracturas.

Fina malla hecha en área rectangular en el software Ansys (método de Elemento Finito)

El método de los elementos finitos

Las estructuras se dividen en elementos discretos de viga 1D, tensión plana 2D o deformación plana, ladrillos 3D o tipos de tetraedro. La continuidad de los elementos se impone utilizando los nodos.

El Método de la Ecuación Integral de Frontera

En este método, la superficie se divide en dos regiones: una región donde los desplazamientos se especifican S_u y una región con tracciones se especifican S_T. Con condiciones de contorno dadas, las tensiones, deformaciones y desplazamientos dentro del cuerpo pueden resolverse teóricamente, junto con las tracciones en S_u y los desplazamientos en S_T. Es una técnica muy poderosa para encontrar las tracciones y desplazamientos desconocidos.

Métodos tradicionales en mecánica computacional de fracturas

Estos métodos se utilizan para determinar los parámetros mecánicos de fractura mediante análisis numérico. Algunos de los métodos tradicionales en mecánica de fractura computacional, que se usaban comúnmente en el pasado, han sido reemplazados por técnicas más nuevas y avanzadas. Las técnicas más nuevas se consideran más precisas y eficientes, lo que significa que pueden proporcionar resultados más precisos y hacerlo más rápidamente que los métodos más antiguos. Vale la pena señalar que no todos los métodos tradicionales se han reemplazado por completo, ya que aún pueden ser útiles en ciertos escenarios, pero es posible que no sean la opción más óptima para todas las aplicaciones.

Algunos de los métodos tradicionales en mecánica de fractura computacional son:

Stress and Displacement matching
Elemental Crack Advance
Integración
Virtual Crack Extension

Contenido relacionado

Más resultados...