Fracción unitaria

Una fracción unitaria es una fracción positiva con uno como numerador, 1/n. Es el inverso multiplicativo (recíproco) del denominador de la fracción, que debe ser un número natural positivo. Los ejemplos son 1/1, 1/2, 1/3, 1/4, 1/5, etc. Cuando un objeto se divide en partes iguales, cada parte es una fracción unitaria del todo.

Multiplicar dos fracciones unitarias produce otra fracción unitaria, pero otras operaciones aritméticas no conservan las fracciones unitarias. En aritmética modular, las fracciones unitarias se pueden convertir en números enteros equivalentes, lo que permite transformar la división modular en multiplicación. Todo número racional se puede representar como una suma de fracciones unitarias distintas; Estas representaciones se denominan fracciones egipcias debido a su uso en las matemáticas del antiguo Egipto. Muchas sumas infinitas de fracciones unitarias tienen significado matemático.

En geometría, las fracciones unitarias se pueden utilizar para caracterizar la curvatura de grupos de triángulos y las tangencias de círculos de Ford. Las fracciones unitarias se utilizan comúnmente en la división equitativa y esta aplicación familiar se utiliza en la educación matemática como un primer paso hacia la comprensión de otras fracciones. Las fracciones unitarias son comunes en la teoría de la probabilidad debido al principio de indiferencia. También tienen aplicaciones en optimización combinatoria y en el análisis del patrón de frecuencias en la serie espectral del hidrógeno.

Aritmética

Las fracciones unitarias son los números racionales que se pueden escribir en la forma

$${displaystyle {frac {}{n}}}$$

${displaystyle n}$

${displaystyle n}$

${displaystyle 1/n}$

Aritmética elemental

Multiplicar dos fracciones unitarias cualesquiera da como resultado un producto que es otra fracción unitaria:

$${displaystyle {frac}times {frac}{y}={frac}={frac} {1}{xy}}$$

$${displaystyle {frac}{x}+{frac} {1}{y}={frac} {x+y}{xy}}$$

$${displaystyle {frac}{x}-{frac} {1} {y}={y-x} {f}} {f}} {f}} {f}} {f}}}} {f}}}} {f}}}}} {f}}}} {f}}}}}} {f}}} {f}}}} {f}}}}}}}}}}}}}}} {\\\\\f}}}}}}}}}}}}}}}}}}}}}}}} {\\\\\\\\\\\\\\\\\\\\\\\fn}}}}}}}}}}}}}}}}}}\\\\\\\\\\\\\\\\\\\\\\\\\\$$

$${displaystyle {frac}{x}div} {fnMicroc {1}{y}={frac} Sí.$$

Como muestra la última de estas fórmulas, cada fracción se puede expresar como un cociente de dos fracciones unitarias.

Aritmética modular

En aritmética modular, cualquier fracción de unidad puede convertirse en un número entero equivalente usando el algoritmo de Euclidean ampliado. Esta conversión se puede utilizar para realizar división modular: dividir por un número ${displaystyle x}$, modulo ${displaystyle y}$, se puede realizar mediante la conversión de la fracción de la unidad ${displaystyle 1/x}$ en un modulo de número entero equivalente ${displaystyle y}$, y luego multiplicarse por ese número.

En más detalle, supongamos que ${displaystyle x}$ es relativamente primo ${displaystyle y}$ (otra vez, división por ${displaystyle x}$ no se define modulo ${displaystyle y}$). El algoritmo extenso de Euclidean para el divisor más común se puede utilizar para encontrar enteros ${displaystyle a}$ y ${displaystyle b}$ tal que la identidad de Bézout esté satisfecha:

$${displaystyle displaystyle ax+by=gcd(x,y)=1.}$$

${displaystyle y}$

${displaystyle by}$

${displaystyle y}$

$${displaystyle displaystyle axequiv 1{pmod {y}}}$$

${displaystyle a}$

${displaystyle x}$

${displaystyle x}$

$${displaystyle aequiv {frac {1}{x}{pmod {}}}$$

${displaystyle x}$

${displaystyle y}$

${displaystyle a}$

Combinaciones

Varias construcciones en matemáticas implican combinar múltiples fracciones unitarias, a menudo sumándolas.

Sumas finitas

Cualquier número racional positivo se puede escribir como la suma de fracciones unitarias distintas, de múltiples maneras. Por ejemplo,

${displaystyle {frac {4}{}={frac} {1}{2}+{frac} {1}{4}+{frac} {1}{20}={frac} {1}{3}+{frac} {1}{5}+{frac} {1}{6}+{frac {1}{10}}$

Estas sumas se llaman fracciones egipcias, porque las antiguas civilizaciones egipcias las usaban como notación para números racionales más generales. Todavía hoy existe interés en analizar los métodos utilizados por los antiguos para elegir entre las posibles representaciones de un número fraccionario y calcular con dichas representaciones. El tema de las fracciones egipcias también ha despertado interés en la teoría de números moderna; por ejemplo, la conjetura de Erdős-Graham y la conjetura de Erdős-Straus se refieren a sumas de fracciones unitarias, al igual que la definición de los números armónicos de Ore.

En la teoría de grupos geométricos, los grupos de triángulos se clasifican en casos euclidianos, esféricos e hiperbólicos según si una suma asociada de fracciones unitarias es igual a uno, mayor que uno o menor que uno, respectivamente.

Serie infinita

Muchas series infinitas conocidas tienen términos que son fracciones unitarias. Éstas incluyen:

• La serie armónica, la suma de todas las fracciones positivas de la unidad. Esta suma se sumerge, y sus sumas parciales
  $${displaystyle {frac {}{1}}+{frac} {1}{2}+{frac} {1}{3}+cdots +{frac {1}{n}}$$

  
  cerca aproxima el logaritmo natural de ${displaystyle n}$ más la constante Euler-Mascheroni. Cambiar cada otra adición a una resta produce la serie armónica alterna, que suma al logaritmo natural de 2:
  $${displaystyle sum _{n=1}{infty }{frac {(-1)^{n+1}{n}}=1-{frac {1}{2}+{frac {1}{3}}-{frac} {1}{4}+{frac} {1}{5}-cdots =ln 2.}$$

  
• La fórmula Leibniz para π es
  $${displaystyle 1-{frac {1}{3}+{frac} {1}{5}-{frac} {1}{7}+{frac} {1}{9}-cdots ={frac {pi} } {4}}$$

  
• El problema de Basilea se refiere a la suma de las fracciones de la unidad cuadrada:
  $${displaystyle 1+{frac {1}{4}+{frac} {1}{9}+{frac} {1}{16}+cdots ={frac {pi ^{2}{6}}}}$$

  
  Del mismo modo, la constante de Apéry es un número irracional, la suma de las fracciones de la unidad cubierta.
• La serie geométrica binaria es
  $${displaystyle 1+{}{2}+{frac} {1}{4}+{frac} {1}{8}+{frac} {1}{16}+cdots =2.}$$

  

Matrices

Una matriz Hilbert es una matriz cuadrada en la que los elementos ${displaystyle i}$T antidiagonal todos iguales a la fracción unidad ${displaystyle 1/i}$. Es decir, tiene elementos

$${displaystyle B_{i,j}={frac {1}{i+j-1}}$$

$${fn} {} {}} {}} {}}} {}}} {}}} {}}} {}} {}} {}} {}} {}}} {}}} {}}} {}} {}} {}} {}} {}} {}} {}} {}} {}} {}}}} {}}} {} {}} {}}}} {}}}}} {}}}}}}}} {}}}}} {}}}}}} {}}} {}} {} {}}}}} {}}}}} {}}}} {}}}}}}}}}} {}}}}}}}}}}}}} {} {} {} {}}}} {}}}}} {}}}}}} {}}}}}} {}}}}} {}}}}}} {}}}}} {}}}} {}}}}}}}}}}}}}}}}}}}}}}$$

$${displaystyle C_{i,j}={frac {1}{i+j-1}}}$$

${displaystyle F_{i}$

${displaystyle i}$T

Adyacencia y círculos de Ford

Dos fracciones ${displaystyle a/b}$ y ${displaystyle c/d}$ (en términos más bajos) se llaman adyacente si

$${displaystyle ad-bc=pm 1,}$$

$${displaystyle lefttención{frac {1}{a}-{frac {1}{b}derecho a la muerte {fnMicrosoft Sans Serif} {fnMicroc} {1}{bd}.}$$

${fnMicroc} {1}{2}}}$

${fnMicroc} {3}{5}}$

${displaystyle 1cdot 5-2cdot 3=-1}$

${displaystyle {tfrac {3}{5}}-{tfrac {1}{2}={tfrac {1}{10}}$

${fnMicroc} {1}{3}}$

${fnMicroc} {2}{3}}$

${displaystyle ad-bc=3}$

Esta terminología proviene del estudio de los círculos de Ford. Estos son un sistema de círculos que son tangentes a la línea número en una fracción determinada y tienen el denominador cuadrado de la fracción como su diámetro. Fracciones ${displaystyle a/b}$ y ${displaystyle c/d}$ son adyacentes si y sólo si sus círculos Ford son círculos tangentes.

Aplicaciones

División justa y educación matemática

En educación matemática, las fracciones unitarias a menudo se introducen antes que otros tipos de fracciones, debido a la facilidad de explicarlas visualmente como partes iguales de un todo. Un uso práctico común de las fracciones unitarias es dividir los alimentos en partes iguales entre varias personas, y los ejercicios para realizar este tipo de división justa son un ejemplo estándar en el aula para enseñar a los estudiantes a trabajar con fracciones unitarias.

Probabilidad y estadística

En una distribución uniforme en un espacio discreto, todas las probabilidades son fracciones unitarias iguales. Debido al principio de indiferencia, probabilidades de esta forma surgen con frecuencia en los cálculos estadísticos.

Las probabilidades inigualables relacionadas con las fracciones unitarias surgen en la ley de Zipf. Esto indica que, para muchos fenómenos observados que implican la selección de elementos de una secuencia ordenada, la probabilidad de que la ${displaystyle n}$T ítem seleccionado es proporcional a la fracción unidad ${displaystyle 1/n}$.

Optimización combinatoria

En el estudio de problemas de optimización combinatoria, los problemas de embalaje de contenedores implican una secuencia de entrada de artículos con tamaños fraccionarios, que deben colocarse en contenedores cuya capacidad (el tamaño total de los artículos colocados en cada contenedor) es uno. La investigación sobre estos problemas ha incluido el estudio de problemas de embalaje en contenedores restringidos donde los tamaños de los artículos son fracciones unitarias.

Una motivación para esto es como un caso de prueba para más métodos generales de empaquetado de basura. Otra implica una forma de programación de pinwheel, en la que una colección de mensajes de igual longitud deben ser transmitidos repetidamente en un número limitado de canales de comunicación, con cada mensaje que tiene un retraso máximo entre los tiempos de inicio de sus repetidas transmisiones. Un tema cuyo retraso es ${displaystyle k}$ tiempos la longitud de un mensaje debe ocupar una fracción de al menos ${displaystyle 1/k}$ de las ranuras de tiempo en el canal que se asigna, por lo que una solución al problema de programación sólo puede venir de una solución al problema de empaquetado de fracción unidad con los canales como contenedores y las fracciones ${displaystyle 1/k}$ como tallas de artículos.

Incluso para problemas de embalaje en contenedores con tamaños de artículos arbitrarios, puede resultar útil redondear cada tamaño de artículo a la siguiente fracción unitaria más grande y luego aplicar un algoritmo de embalaje en contenedores especializado para tamaños de fracciones unitarias. En particular, el método de embalaje de contenedores armónicos hace exactamente esto y luego empaqueta cada contenedor utilizando artículos de un solo tamaño de fracción unitaria redondeada.

Física

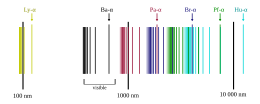
Los niveles de energía de los fotones que puede absorber o emitir un átomo de hidrógeno son, según la fórmula de Rydberg, proporcionales a las diferencias de dos fracciones unitarias. Una explicación para este fenómeno la proporciona el modelo de Bohr, según el cual los niveles de energía de los orbitales de los electrones en un átomo de hidrógeno son inversamente proporcionales a las fracciones unitarias cuadradas, y la energía de un fotón se cuantifica a la diferencia entre dos niveles.

Arthur Eddington argumentó que la constante de estructura fina era una fracción unitaria. Inicialmente pensó que era 1/136 y luego cambió su teoría a 1/137. Esta afirmación ha sido refutada, dado que las estimaciones actuales de la constante de estructura fina son (hasta 6 dígitos significativos) 1/137,036.