Fotoelasticidad

En ciencia de materiales, la fotoelasticidad describe cambios en las propiedades ópticas de un material bajo deformación mecánica. Es una propiedad de todos los medios dieléctricos y a menudo se utiliza para determinar experimentalmente la distribución de tensiones en un material.
Historia
El fenómeno fotoelástico fue descubierto por primera vez por el físico escocés David Brewster, quien inmediatamente lo reconoció como birrefringencia inducida por estrés. Ese diagnóstico fue confirmado en un experimento de refracción directa realizado por Augustin-Jean Fresnel. Los marcos experimentales se desarrollaron a principios del siglo XX con los trabajos de E. G. Coker y L. N. G. Filon de la Universidad de Londres. Su libro Tratado sobre fotoelasticidad, publicado en 1930 por Cambridge Press, se convirtió en un texto estándar sobre el tema. Entre 1930 y 1940 aparecieron muchos otros libros sobre el tema, incluidos libros en ruso, alemán y francés. Max M. Frocht publicó la clásica obra en dos volúmenes, Fotoelasticidad, sobre el terreno. Al mismo tiempo, se produjo un gran desarrollo en el campo: se lograron grandes mejoras en la técnica y se simplificó el equipo. Con los perfeccionamientos de la tecnología, los experimentos fotoelásticos se ampliaron para determinar estados de tensión tridimensionales. Paralelamente a los avances en la técnica experimental, la primera descripción fenomenológica de la fotoelasticidad la dio Friedrich Pockels en 1890; sin embargo, casi un siglo después, Nelson & Laxo, como lo describió Pockels, solo consideró el efecto de la tensión mecánica sobre las propiedades ópticas del material.
Con la llegada del polariscopio digital, posible gracias a los diodos emisores de luz, se hizo posible el monitoreo continuo de estructuras bajo carga. Esto condujo al desarrollo de la fotoelasticidad dinámica, que ha contribuido en gran medida al estudio de fenómenos complejos como la fractura de materiales.
Aplicaciones

La fotoelasticidad se ha utilizado para una variedad de análisis de tensiones e incluso para uso rutinario en el diseño, particularmente antes de la llegada de los métodos numéricos, como los elementos finitos o los elementos de contorno. La digitalización de la polariscocopia permite una rápida adquisición de imágenes y procesamiento de datos, lo que permite que sus aplicaciones industriales controlen la calidad del proceso de fabricación de materiales como el vidrio y los polímeros. La odontología utiliza la fotoelasticidad para analizar la tensión en los materiales de las dentaduras postizas.
La fotoelasticidad se puede utilizar con éxito para investigar el estado de tensión altamente localizado dentro de la mampostería o en las proximidades de una inclusión de línea rígida (refuerzo) incrustada en un medio elástico. En el primer caso, el problema es no lineal debido a los contactos entre ladrillos, mientras que en el segundo caso la solución elástica es singular, por lo que los métodos numéricos pueden no proporcionar resultados correctos. Estos se pueden obtener mediante técnicas fotoelásticas. La fotoelasticidad dinámica integrada con fotografía de alta velocidad se utiliza para investigar el comportamiento de fractura en materiales. Otra aplicación importante de los experimentos de fotoelasticidad es estudiar el campo de tensión alrededor de muescas bimateriales. Las muescas bimateriales existen en muchas aplicaciones de ingeniería, como estructuras soldadas o unidas con adhesivo.
Definición formal
Para un material dieléctrico lineal el cambio en el tensor de la permittividad inversa Δ Δ ()ε ε − − 1)ij{displaystyle Delta (varepsilon ^{-1}_{ij}} con respecto a la deformación (el gradiente del desplazamiento ∂ ∂ l l uk{displaystyle partial _{ell }u_{k}) se describe por
- Δ Δ ()ε ε − − 1)ij=Pijkl l ∂ ∂ kul l {displaystyle Delta (varepsilon ^{-1}_{ij}=P_{ijkell }partial _{k}u_{ell }
Donde Pijkl l {displaystyle P_{ijkell } es el tensor fotoelástica de cuarto rango, ul l {displaystyle u_{ell } es el desplazamiento lineal del equilibrio, y ∂ ∂ l{displaystyle partial _{l} denota diferenciación con respecto a la coordinación cartesiana xl{displaystyle x_{l}. Para materiales isotrópicos, esta definición simplifica
- Δ Δ ()ε ε − − 1)ij=pijkl l skl l {displaystyle Delta (varepsilon ^{-1}_{ijkell }s_{kell }
Donde pijkl l {displaystyle p_{ijkell } es la parte simétrica del tensor fotoelástico (el tensor fotoelástico), y skl l {displaystyle s_{kell } es la tensión lineal. La parte antisimétrica de Pijkl l {displaystyle P_{ijkell } es conocido como el tensor roto-optico. De cualquier definición, está claro que las deformaciones al cuerpo pueden inducir a la anisotropía óptica, lo que puede causar que un material isotrópico de otro modo exponga birefringencia. Aunque el tensor fotoelástico simétrico es más comúnmente definido con respecto a la tensión mecánica, también es posible expresar fotoelástica en términos de estrés mecánico.
Principios experimentales

El procedimiento experimental se basa en la propiedad de birrefringencia, exhibida por ciertos materiales transparentes. La birrefringencia es un fenómeno en el que un rayo de luz que atraviesa un material determinado experimenta dos índices de refracción. La propiedad de birrefringencia (o doble refracción) se observa en muchos cristales ópticos. Tras la aplicación de tensiones, los materiales fotoelásticos exhiben la propiedad de birrefringencia, y la magnitud de los índices de refracción en cada punto del material está directamente relacionada con el estado de las tensiones en ese punto. Información como la tensión cortante máxima y su orientación están disponibles analizando la birrefringencia con un instrumento llamado polariscopio.
Cuando un rayo de luz pasa a través de un material fotoelástico, sus componentes de onda electromagnética se resuelven a lo largo de las dos direcciones principales de tensión y cada componente experimenta un índice de refracción diferente debido a la birrefringencia. La diferencia en los índices de refracción conduce a un retraso de fase relativo entre los dos componentes. Suponiendo una muestra delgada hecha de materiales isotrópicos, donde es aplicable la fotoelasticidad bidimensional, la magnitud del retardo relativo viene dada por la ley óptica de tensión:
- Δ Δ =2π π tλ λ C()σ σ 1− − σ σ 2){displaystyle Delta ={frac {2ccH00} t}{lambda #C(sigma _{1}-sigma ¿Qué?
donde Δ es el retraso inducido, C es el coeficiente de tensión óptica, t es el espesor de la muestra, λ es la longitud de onda de vacío y σ1 y σ2 son las tensiones principales primera y segunda, respectivamente. El retardo cambia la polarización de la luz transmitida. El polariscopio combina los diferentes estados de polarización de las ondas de luz antes y después de pasar por la muestra. Debido a la interferencia óptica de las dos ondas, se revela un patrón de franjas. El número de orden marginal N se denota como
- N=Δ Δ 2π π {displaystyle N={frac {Delta}{2pi}}}
que depende del retraso relativo. Al estudiar el patrón de franjas se puede determinar el estado de tensión en varios puntos del material.
Para materiales que no muestran comportamiento fotoelástico, aún es posible estudiar la distribución de tensiones. El primer paso es construir un modelo, utilizando materiales fotoelásticos, que tenga una geometría similar a la estructura real que se está investigando. Luego, la carga se aplica de la misma manera para garantizar que la distribución de tensiones en el modelo sea similar a la tensión en la estructura real.
Isoclínicas e isocromáticas
Las isoclínicas son los lugares geométricos de los puntos de la muestra a lo largo de los cuales las tensiones principales están en la misma dirección.
Las isocromáticas son los lugares geométricos de los puntos a lo largo de los cuales la diferencia en la primera y segunda tensión principal sigue siendo la misma. Por tanto, son las líneas que unen los puntos con igual magnitud máxima de esfuerzo cortante.
Fotoelasticidad bidimensional

La fotoelasticidad puede describir estados de tensión tanto tridimensionales como bidimensionales. Sin embargo, examinar la fotoelasticidad en sistemas tridimensionales es más complicado que en sistemas bidimensionales o de tensión plana. Por tanto, la presente sección trata de la fotoelasticidad en un sistema de tensiones plano. Esta condición se logra cuando el espesor del prototipo es mucho menor en comparación con las dimensiones en el plano. Por lo tanto, sólo nos preocupan las tensiones que actúan paralelas al plano del modelo, ya que otros componentes de las tensiones son cero. La configuración experimental varía de un experimento a otro. Los dos tipos básicos de configuración utilizados son el polariscopio plano y el polariscopio circular.
El principio de funcionamiento de un experimento bidimensional permite la medición del retardo, que se puede convertir en la diferencia entre la primera y la segunda tensión principal y su orientación. Para obtener más valores de cada componente de tensión, se requiere una técnica llamada separación de tensiones. Se utilizan varios métodos teóricos y experimentales para proporcionar información adicional para resolver componentes de tensión individuales.
Configuración del polariscopio plano
La configuración consta de dos polarizadores lineales y una fuente de luz. La fuente de luz puede emitir luz monocromática o luz blanca según el experimento. Primero, la luz pasa a través del primer polarizador que la convierte en luz polarizada plana. El aparato está configurado de tal manera que esta luz polarizada plana atraviese la muestra sometida a tensión. Esta luz sigue entonces, en cada punto de la muestra, la dirección de la tensión principal en ese punto. Luego se hace pasar la luz a través del analizador y finalmente obtenemos el patrón de franjas.
El patrón de franjas en una configuración de polariscopio plano consta tanto de isocromáticas como de isoclínicas. Las isoclínicas cambian con la orientación del polariscopio mientras que no hay cambios en las isocromáticas.
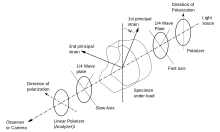
El mismo dispositivo funciona como un polariscopio plano cuando las placas de onda trimestral se toman a un lado o giran por lo que sus ejes paralelos a los ejes de polarización
Configuración del polariscopio circular
En una configuración de polariscopio circular se agregan dos placas de cuarto de onda a la configuración experimental del polariscopio plano. La primera placa de cuarto de onda se coloca entre el polarizador y la muestra y la segunda placa de cuarto de onda se coloca entre la muestra y el analizador. El efecto de agregar la placa de cuarto de onda después del polarizador del lado de la fuente es que obtenemos luz polarizada circularmente que pasa a través de la muestra. La placa de cuarto de onda del lado del analizador convierte el estado de polarización circular nuevamente a lineal antes de que la luz pase a través del analizador.
La ventaja básica de un polariscopio circular sobre un polariscopio plano es que en una configuración de polariscopio circular solo obtenemos las isocromáticas y no las isoclínicas. Esto elimina el problema de diferenciar entre las isoclínicas y las isocromáticas.
Contenido relacionado
Precisión y exactitud
Evidencia empírica
Teoría del flogisto











