Fórmula barométrica

format_list_bulleted Contenido keyboard_arrow_down

ImprimirCitar

Fórmula utilizada para modelar cómo la presión del aire varía con altitud

La fórmula barométrica es una fórmula que se utiliza para modelar cómo la presión (o densidad) del aire cambia con la altitud.

Ecuaciones de presión

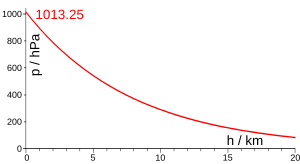
Hay dos ecuaciones para la presión de cálculo como función de la altura. La primera ecuación es aplicable a las capas atmosféricas en las que se supone que la temperatura varía con altitud a una tasa de lapso no nula ${displaystyle L_{b}}$ :

{displaystyle P=P_{b}left[1-{frac {L_{M,b}}{T_{M,b}}}(h-h_{b})right]^{frac {g_{0}'M_{0}}{R^{*}L_{M,b}}}}

{displaystyle P=P_{b}exp left[{frac {-g_{0}Mleft(h-h_{b}right)}{R^{*}{T_{M,b}}}}right]}

${displaystyle P_{b}}$ = presión de referencia
${displaystyle T_{M,b}}$ = temperatura de referencia (K)
${displaystyle L_{M,b}}$ = tasa de lapso de temperatura (K/m) en ISA
${displaystyle h}$ = altura a la que se calcula la presión (m)
${displaystyle h_{b}}$ = altura del nivel de referencia b (meters; e.g., h_b = 11 000 m)
${displaystyle R^{*}}$ = constante de gas universal: 8.3144598 J/(mol·K)
${displaystyle g_{0}}$ = aceleración gravitacional: 9.80665 m/s²
${displaystyle M}$ = masa molar del aire de la Tierra: 0,028964425278793993 kg/mol

O convertido a unidades imperiales:

${displaystyle P_{b}}$ = presión de referencia
${displaystyle T_{M,b}}$ = temperatura de referencia (K)
${displaystyle L_{M,b}}$ = tasa de lapso de temperatura (K/ft) en ISA
${displaystyle h}$ = altura a la que se calcula la presión (ft)
${displaystyle h_{b}}$ = altura del nivel de referencia b ( pies; por ejemplo, h_b = 36,089 pies)
${displaystyle R^{*}}$ = constante de gas universal; usando pies, kelvins y (SI) lunares: 8.9494596×10⁴ lb·ft²/(lb-mol·K·s²)
${displaystyle g_{0}}$ = aceleración gravitacional: 32.17405 pies/s²
${displaystyle M}$ = masa molar del aire de la Tierra: 28.9644 lb/lb-mol

El valor del subíndice b varía de 0 a 6 de acuerdo con cada una de las siete capas sucesivas de la atmósfera que se muestran en la siguiente tabla. En estas ecuaciones, g₀, M y R^* son cada uno de ellos constantes valoradas, mientras que P, L, T, y h son constantes multivaloradas de acuerdo con la siguiente tabla. Los valores utilizados para M, g₀ y R^* están de acuerdo con la atmósfera estándar de EE. UU. de 1976, y el valor de R^* en particular no concuerda con los valores estándar de esta constante. El valor de referencia para P_b para b = 0 es el valor definido del nivel del mar, P₀ = 101 325 Pa o 29,92126 inHg. Los valores de P_b de b = 1 a b = 6 se obtienen de la aplicación del miembro apropiado de el par de ecuaciones 1 y 2 para el caso en que h = h_b+1.

Subscript b	Geopotencial altura sobre MSL h)		Presión estatica		Temperatura estándar (K)	Tasa de lapso de temperatura		Exponent g0 M / R L
Subscript b	m)	(ft)	(Pa)	(inHg)	Temperatura estándar (K)	(K/m)	(K/ft)	Exponent g0 M / R L
0	0	0	101 325.00	29.92126	288.15	0,0065	0,0019812	5.2558
1	11 000	36.089	22 632.10	6.683245	216.65	0,0	0,0	—
2	20 000	65.617	5474.89	1.616734	216.65	-0.001	-0.0003048	-34.1626
3	32 000	104.987	868.02	0,263258	228.65	-0.0028	-0.00085344	-12.2009
4	47 000	154.199	110.91	0,0327506	270.65	0,0	0,0	—
5	51 000	167,323	66.94	0,01976704	270.65	0,0028	0,00085344	12.2009
6	71 000	232,940	3.96	0,00116833	214.65	0,002	0,0006096	17.0813

Ecuaciones de densidad

Las expresiones para calcular la densidad son casi idénticas a las del cálculo de la presión. La única diferencia es el exponente de la Ecuación 1.

Hay dos ecuaciones para la densidad de cálculo como función de la altura. La primera ecuación es aplicable al modelo estándar de la troposfera en que se supone que la temperatura varía con altitud a una velocidad de lapso ${displaystyle L_{b}}$ ; la segunda ecuación es aplicable al modelo estándar de la estratosfera en el que se supone que la temperatura no varía con altitud.

Ecuación 1:

{displaystyle rho =rho _{b}left[{frac {T_{b}-(h-h_{b})L_{b}}{T_{b}}}right]^{left({frac {g_{0}M}{R^{*}L_{b}}}-1right)}}

que es equivalente a la relación entre los cambios relativos de presión y temperatura

{displaystyle rho =rho _{b}{frac {P}{T}}{frac {T_{b}}{P_{b}}}}

Ecuación 2:

{displaystyle rho =rho _{b}exp left[{frac {-g_{0}Mleft(h-h_{b}right)}{R^{*}T_{b}}}right]}

dónde

${displaystyle {rho }}$ = densidad de masa (kg/m³)
${displaystyle T_{b}}$ = temperatura estándar (K)
${displaystyle L}$ = tasa de lapso de temperatura estándar (véase el cuadro que figura a continuación) (K/m) en ISA
${displaystyle h}$ = altura sobre el nivel del mar (metros geopotenciales)
${displaystyle R^{*}}$ = constante de gas universal 8.3144598 N·m/(mol·K)
${displaystyle g_{0}}$ = aceleración gravitacional: 9.80665 m/s²
${displaystyle M}$ = masa molar del aire de la Tierra: 0.0289644 kg/mol

o, convertido a unidades gravitacionales pie-libra-segundo estadounidenses (ya no se utilizan en el Reino Unido):

${displaystyle {rho }}$ = densidad de masa (slug/ft³)
${displaystyle {T_{b}}}$ = temperatura estándar (K)
${displaystyle {L}}$ = tasa de lapso de temperatura estándar (K/ft)
${displaystyle {h}}$ = altura sobre el nivel del mar (pies geopotenciales)
${displaystyle {R^{*}}}$ = constante de gas universal: 8.9494596×10⁴ f²/(s·K)
${displaystyle {g_{0}}}$ = aceleración gravitacional: 32.17405 pies/s²
${displaystyle {M}}$ = masa molar del aire de la Tierra: 0.0289644 kg/mol

El valor del subíndice b varía de 0 a 6 de acuerdo con cada una de las siete capas sucesivas de la atmósfera que se muestran en la siguiente tabla. El valor de referencia para ρ_b para b = 0 es el valor definido del nivel del mar, ρ₀ = 1,2250 kg/m³ o 0,0023768908 slug/pie³. Los valores de ρ_b de b = 1 a b = 6 se obtienen de la aplicación del miembro apropiado de el par de ecuaciones 1 y 2 para el caso en que h = h_b+1.

En estas ecuaciones, g₀, M y R^* son cada una de las constantes valoradas, mientras ***, L, T y h son constantes de valor múltiple de acuerdo con la tabla siguiente. Los valores utilizados para M, g₀ y R^* están de acuerdo con la atmósfera estándar estadounidense, 1976, y que el valor para R^* en particular no está de acuerdo con los valores estándar para esta constante.

Subscript b	Geopotencial altura sobre MSL h)		Densidad de Masa ${displaystyle rho }$ )		Temperatura estándar (T ') (K)	Tasa de lapso de temperatura (L)
Subscript b	m)	(ft)	(kg/m³)	(slug/ft³)	Temperatura estándar (T ') (K)	(K/m)	(K/ft)
0	0	0	1.2250	2.3768908×10⁻³	288.15	0,0065	0,0019812
1	11 000	36,089.24	0,6391	7.0611703×10⁻⁴	216.65	0,0	0,0
2	20 000	65,616.79	0,08803	1.7081572×10⁻⁴	216.65	-0.001	-0.0003048
3	32 000	104,986.87	0,01322	2.5660735×10^{; 5 -}	228.65	-0.0028	-0.00085344
4	47 000	154.199.48	0,00143	2.7698702×10⁻⁶	270.65	0,0	0,0
5	51 000	167,322.83	0,00086	1.6717895×10⁻⁶	270.65	0,0028	0,00085344
6	71 000	232,939.63	0,000064	1.2458989×10⁻⁷	214.65	0,002	0,0006096

Derivación

La fórmula barométrica se puede derivar utilizando la ley de los gases ideales:

{displaystyle P={frac {rho }{M}}{R^{*}}T}

Suponiendo que toda la presión es hidrostática:

{displaystyle dP=-rho g,dz}

{displaystyle P}

{displaystyle {frac {dP}{P}}=-{frac {Mg,dz}{R^{*}T}}}

Integrando esta expresión desde la superficie a la altitud z obtenemos:

{displaystyle P=P_{0}e^{-int _{0}^{z}{Mgdz/R^{*}T}}}

Asumiendo el cambio de temperatura lineal ${displaystyle T=T_{0}-Lz}$ y constante masa molar y aceleración gravitacional, obtenemos la primera fórmula barométrica:

{displaystyle P=P_{0}cdot left[{frac {T}{T_{0}}}right]^{textstyle {frac {Mg}{R^{*}L}}}}

En cambio, asumiendo una temperatura constante, la integración da la segunda fórmula barométrica:

{displaystyle P=P_{0}e^{-Mgz/R^{*}T}}

En esta formulación, R^* es la constante de los gases y el término R^*T/Mg da la altura de la escala (aproximadamente igual a 8,4 km para la troposfera).

(Para obtener resultados exactos, se debe recordar que las atmósferas que contienen agua no se comportan como un gas ideal. Consulte gas real o gas perfecto o gas para una mayor comprensión).

Contenido relacionado

Más resultados...