Flujo potencial

ImprimirCitar

Campo de la velocidad como el gradiente de una función de escalar

El flujo potencial simplifica alrededor de un avión NACA 0012 a un ángulo de ataque de 11°, con secuencias superiores e inferiores identificadas. El flujo es bidimensional y el flujo de aire tiene un lazo infinito.

En dinámica de fluidos, el flujo potencial (o flujo ideal) describe el campo de velocidad como el gradiente de una función escalar: el potencial de velocidad. Como resultado, un flujo potencial se caracteriza por un campo de velocidad irrotacional, que es una aproximación válida para varias aplicaciones. La irrotacionalidad de un flujo potencial se debe a que el rotacional del gradiente de un escalar es siempre igual a cero.

En el caso de un flujo incompresible, el potencial de velocidad satisface la ecuación de Laplace y se aplica la teoría del potencial. Sin embargo, los flujos potenciales también se han utilizado para describir flujos compresibles. El enfoque de flujo potencial ocurre en el modelado de flujos tanto estacionarios como no estacionarios. Las aplicaciones del flujo potencial son, por ejemplo: el campo de flujo externo para superficies aerodinámicas, ondas de agua, flujo electroosmótico y flujo de agua subterránea. Para flujos (o partes de ellos) con fuertes efectos de vorticidad, la aproximación de flujo potencial no es aplicable.

Características y aplicaciones

Un flujo potencial se construye añadiendo flujos elementales simples y observando el resultado.

Streamlines for the incompressible potential flow around a circular cilindro in a uniform onflow.

Descripción y características

En dinámica de fluidos, un flujo potencial se describe mediante un potencial de velocidad $φ$ , siendo una función del espacio y el tiempo. La velocidad del flujo $v$ es un campo vectorial igual al gradiente, $\nabla$ , del potencial de velocidad $φ$ :

{mathbf {v}}=nabla varphi.

A veces, también se usa la definición $v = -\nabla φ$ , con un signo menos. Pero aquí usaremos la definición anterior, sin el signo menos. Del cálculo vectorial se sabe que el rotacional de un gradiente es igual a cero:

{displaystyle nabla times nabla varphi =mathbf {0} ,,}

y consecuentemente la vorticidad, el rotacional del campo de velocidad $v$ , es cero:

{displaystyle nabla times mathbf {v} =mathbf {0} ,.}

Esto implica que un flujo potencial es un flujo irrotacional. Esto tiene consecuencias directas para la aplicabilidad del flujo potencial. En las regiones de flujo donde se sabe que la vorticidad es importante, como las estelas y las capas límite, la teoría del flujo potencial no puede proporcionar predicciones razonables del flujo. Afortunadamente, a menudo hay grandes regiones de un flujo donde la suposición de irrotacionalidad es válida, razón por la cual el flujo potencial se usa para varias aplicaciones. Por ejemplo, en: flujo alrededor de aeronaves, flujo de aguas subterráneas, acústica, ondas de agua y flujo electroosmótico.

Flujo incompresible

En el caso de un flujo incompresible, por ejemplo, de un líquido o un gas con números de Mach bajos; pero no para las ondas sonoras: la velocidad $v$ tiene divergencia cero:

{displaystyle nabla cdot mathbf {v} =0,,}

con el punto que denota el producto interior. Como resultado, el potencial de velocidad $φ$ tiene que satisfacer la ecuación de Laplace

{displaystyle nabla ^{2}varphi =0,,}

donde $\nabla 2 = \nabla \cdot \nabla$ es el operador de Laplace (a veces también escrito $Δ$ ). En este caso, el flujo se puede determinar completamente a partir de su cinemática: los supuestos de irrotacionalidad y divergencia cero del flujo. La dinámica solo debe aplicarse después, si uno está interesado en calcular presiones: por ejemplo, para flujo alrededor de superficies aerodinámicas mediante el uso del principio de Bernoulli.

En dos dimensiones, el flujo potencial se reduce a un sistema muy simple que se analiza mediante un análisis complejo (ver más abajo).

Flujo compresible

Flujo constante

La teoría del flujo potencial también se puede utilizar para modelar el flujo compresible irrotacional. La ecuación de potencial total, que describe un flujo constante, está dada por:

{displaystyle left(1-M_{x}^{2}right){frac {partial ^{2}Phi }{partial x^{2}}}+left(1-M_{y}^{2}right){frac {partial ^{2}Phi }{partial y^{2}}}+left(1-M_{z}^{2}right){frac {partial ^{2}Phi }{partial z^{2}}}-2M_{x}M_{y}{frac {partial ^{2}Phi }{partial x,partial y}}-2M_{y}M_{z}{frac {partial ^{2}Phi }{partial y,partial z}}-2M_{z}M_{x}{frac {partial ^{2}Phi }{partial z,partial x}}=0,,}

con componentes de número de Mach

{displaystyle {begin{aligned}M_{x}&={frac {1}{a}}{frac {partial Phi }{partial x}},,&M_{y}&={frac {1}{a}}{frac {partial Phi }{partial y}},,{text{ and }}&M_{z}&={frac {1}{a}}{frac {partial Phi }{partial z}},,end{aligned}}}

donde $a$ es la velocidad local del sonido. La velocidad del flujo $v$ vuelve a ser igual a $\nablaΦ$ , con $Φ$ el potencial de velocidad. La ecuación de potencial total es válida para flujos sub, trans y supersónicos en ángulos de ataque arbitrarios, siempre que se aplique la suposición de irrotacionalidad.

En el caso de un flujo subsónico o supersónico (pero no transónico o hipersónico), en ángulos de ataque pequeños y cuerpos delgados, se puede hacer una suposición adicional: el potencial de velocidad se divide en una velocidad de flujo de entrada no perturbada $V \infty$ en $x$ - dirección, y una pequeña velocidad de perturbación $\nabla φ$ del mismo. Entonces:

{displaystyle nabla Phi =V_{infty }x+nabla varphi ,.}

En ese caso, se puede usar la ecuación de potencial de perturbación pequeña linealizada, una aproximación a la ecuación de potencial completa:

{displaystyle left(1-M_{infty }^{2}right){frac {partial ^{2}varphi }{partial x^{2}}}+{frac {partial ^{2}varphi }{partial y^{2}}}+{frac {partial ^{2}varphi }{partial z^{2}}}=0,}

con $M \infty = <span class="num" V \infty / a \infty$ el número de Mach del flujo libre entrante. Esta ecuación lineal es mucho más fácil de resolver que la ecuación potencial completa: se puede reformular en la ecuación de Laplace mediante un simple estiramiento de coordenadas en el $x$ .

Derivación de la ecuación de potencial completo

Para un flujo inviscido constante, las ecuaciones de Euler —para la densidad de masa y ímpetu— están, en notación de subscriptos y en forma de no conservación:

{displaystyle {begin{aligned}{frac {partial }{partial x_{i}}}left(rho ,v_{i}right)&=0,,\rho ,v_{j},{frac {partial v_{i}}{partial x_{j}}}&=-{frac {partial p}{partial x_{i}}},,end{aligned}}}

mientras utiliza la convención de la suma: desde $j$ ocurre más de una vez en el término en el lado izquierdo de la ecuación de impulso, $j$ se resume sobre todos sus componentes (que es de 1 a 2 en flujo bidimensional, y de 1 a 3 en tres dimensiones). Further:

$***$ es la densidad del fluido,
$p$ es la presión,
$() x 1, x 2, x 3) = x, Sí., z)$ son las coordenadas y
$() v 1, v 2, v 3)$ son los componentes correspondientes del vector de velocidad $v$ .

La velocidad del sonido cuadrada $a 2$ es igual al derivado de la presión $p$ con respecto a la densidad $***$ , en constante entropía $S$ :

a^{2}=left[{frac {partial p}{partial rho }}right]_{S}.

Como resultado, las ecuaciones de flujo se pueden escribir como:

{displaystyle {begin{aligned}v_{i},{frac {partial rho }{partial x_{i}}}+rho ,{frac {partial v_{i}}{partial x_{i}}}&=0,,{text{ and }}&rho ,v_{j},{frac {partial v_{i}}{partial x_{j}}}&=-a^{2},{frac {partial rho }{partial x_{i}}},.end{aligned}}}

Multiplicar (y resumir) la ecuación de impulso con $v i$ , y el uso de la ecuación de masa para eliminar el gradiente de densidad da:

{displaystyle rho ,v_{i},v_{j},{frac {partial v_{i}}{partial x_{j}}}=rho ,a^{2},{frac {partial v_{i}}{partial x_{i}}},.}

Cuando se divide por $***$ , y con todos los términos en un lado de la ecuación, la ecuación de flujo compresible es:

{displaystyle {frac {partial v_{i}}{partial x_{i}}}-{frac {v_{i},v_{j}}{a^{2}}}{frac {partial v_{i}}{partial x_{j}}}=0,.}

Tenga en cuenta que hasta esta etapa no se han hecho supuestos sobre el flujo (además de que es un flujo constante).

Ahora, para el flujo irrotacional la velocidad $v$ es el gradiente del potencial de velocidad $CCPR$ , y los componentes locales del número Mach $M i$ se definen como:

{displaystyle {begin{aligned}v_{i}&={frac {partial Phi }{partial x_{i}}},,{text{ and }}&M_{i}&={frac {v_{i}}{a}}={frac {1}{a}}{frac {partial Phi }{partial x_{i}}},.end{aligned}}}

Cuando se utiliza en la ecuación de flujo, la ecuación de potencial completo resulta:

{displaystyle {frac {partial ^{2}Phi }{partial x_{i},partial x_{i}}}-M_{i},M_{j},{frac {partial ^{2}Phi }{partial x_{i},partial x_{j}}}=0,.}

Escrita en componentes, se obtiene la forma dada al comienzo de esta sección. Cuando se proporciona una ecuación específica de estado, se relaciona la presión $p$ y densidad $***$ , la velocidad del sonido se puede determinar. Posteriormente, junto con las condiciones de límites adecuadas, se puede resolver la ecuación total potencial (la mayoría a menudo mediante el uso de un código de dinámica de fluido computacional).

Flujo inestable

La teoría del flujo potencial también se puede utilizar para modelar el flujo compresible irrotacional. La ecuación de potencial total, que describe un flujo no estacionario, está dada por:

{displaystyle {begin{aligned}0=-{frac {1}{a^{2}}}left[{frac {partial }{partial t}}(nabla Phi cdot nabla Phi)+{frac {partial ^{2}Phi }{partial t^{2}}}right]&+left(1-M_{x}^{2}right){frac {partial ^{2}Phi }{partial x^{2}}}+left(1-M_{y}^{2}right){frac {partial ^{2}Phi }{partial y^{2}}}+left(1-M_{z}^{2}right){frac {partial ^{2}Phi }{partial z^{2}}}\[3pt]&-2M_{x}M_{y}{frac {partial ^{2}Phi }{partial x,partial y}}-2M_{y}M_{z}{frac {partial ^{2}Phi }{partial y,partial z}}-2M_{z}M_{x}{frac {partial ^{2}Phi }{partial z,partial x}}end{aligned}}}

con componentes de número de Mach

{displaystyle {begin{aligned}M_{x}&={frac {1}{a}}{frac {partial Phi }{partial x}},,&M_{y}&={frac {1}{a}}{frac {partial Phi }{partial y}},,{text{ and }}&M_{z}&={frac {1}{a}}{frac {partial Phi }{partial z}},,end{aligned}}}

donde $a$ es la velocidad local del sonido. La velocidad del flujo $v$ vuelve a ser igual a $\nablaΦ$ , con $Φ$ el potencial de velocidad. La ecuación de potencial total es válida para el flujo sub, trans y supersónico en un ángulo de ataque arbitrario, siempre que se aplique la suposición de irrotacionalidad.

{displaystyle nabla Phi =V_{infty }x+nabla varphi ,.}

En ese caso, se puede usar la ecuación de potencial de perturbación pequeña linealizada, una aproximación a la ecuación de potencial completa:

{displaystyle -{frac {1}{a^{2}}}left[2V_{infty }{frac {partial ^{2}varphi }{partial xpartial t}}+{frac {partial ^{2}varphi }{partial t^{2}}}right]+left(1-M_{infty }^{2}right){frac {partial ^{2}varphi }{partial x^{2}}}+{frac {partial ^{2}varphi }{partial y^{2}}}+{frac {partial ^{2}varphi }{partial z^{2}}}=0,}

con $M \infty = <span class="num" V \infty / a \infty$ el número de Mach del flujo libre entrante.

Derivación de la ecuación de potencial completo

Comenzaremos con ecuación de conservación masiva

{displaystyle {frac {1}{rho }}{frac {partial rho }{partial t}}+{frac {{vec {v}}cdot nabla rho }{rho }}+nabla cdot {vec {v}}=0}

Considere el primer término. Usando el principio de Bernoulli escribimos

{displaystyle {frac {1}{rho }}{frac {partial rho }{partial t}}={frac {1}{a^{2}rho }}{frac {partial p}{partial t}}={frac {1}{a^{2}}}{frac {partial }{partial t}}int _{p_{1}}^{p}{frac {d{tilde {p}}}{drho ({tilde {p}})}}=-{frac {1}{a^{2}}}{frac {partial }{partial t}}left[{frac {partial Phi }{partial t}}+{frac {nabla Phi cdot nabla Phi }{2}}right]}

De manera similar, el segundo término puede ser escrito

{displaystyle {frac {{vec {v}}cdot nabla rho }{rho }}={frac {{vec {v}}cdot nabla p}{a^{2}rho }}=-{frac {1}{a^{2}}}{vec {v}}cdot nabla left[{frac {partial Phi }{partial t}}+{frac {nabla Phi cdot nabla Phi }{2}}right]=-{frac {1}{a^{2}}}nabla Phi cdot nabla left[{frac {partial Phi }{partial t}}+{frac {nabla Phi cdot nabla Phi }{2}}right]}

Recoger términos, y reorganizar, la ecuación de conservación de masas se convierte en

{displaystyle {begin{aligned}nabla ^{2}Phi -{frac {1}{a^{2}}}{frac {partial }{partial t}}left[{frac {partial Phi }{partial t}}+{frac {nabla Phi cdot nabla Phi }{2}}right]-{frac {1}{a^{2}}}nabla Phi cdot nabla left[{frac {partial Phi }{partial t}}+{frac {nabla Phi cdot nabla Phi }{2}}right]&=0\Rightarrow nabla ^{2}Phi -{frac {1}{a^{2}}}left[{frac {partial ^{2}Phi }{partial t^{2}}}+{frac {partial }{partial t}}(nabla Phi cdot nabla Phi)+nabla Phi cdot nabla left({frac {nabla Phi cdot nabla Phi }{2}}right)right]&=0end{aligned}}}

Ondas de sonido

Las ondas sonoras de pequeña amplitud se pueden aproximar con el siguiente modelo de flujo potencial:

frac{partial^2 varphi}{partial t^2} = overline{a}^2 Delta varphi,

que es una ecuación de onda lineal para el potencial de velocidad $φ$ . De nuevo, la parte oscilatoria del vector de velocidad $v$ está relacionada con el potencial de velocidad por $v = \nabla φ$ , mientras que antes $Δ$ es el operador de Laplace, y $ā$ es la velocidad media del sonido en el medio homogéneo. Tenga en cuenta que también las partes oscilatorias de la presión $p$ y la densidad $ρ$ cada uno satisface individualmente la ecuación de onda, en esta aproximación.

Aplicabilidad y limitaciones

El flujo potencial no incluye todas las características de los flujos que se encuentran en el mundo real. La teoría del flujo potencial no se puede aplicar a los flujos internos viscosos, excepto a los flujos entre placas estrechamente espaciadas. Richard Feynman consideró que el flujo potencial era tan poco físico que el único fluido que obedecía a los supuestos era el 'agua seca'. (citando a John von Neumann). El flujo potencial incompresible también hace una serie de predicciones no válidas, como la paradoja de d'Alembert, que establece que el arrastre de cualquier objeto que se mueve a través de un fluido infinito en reposo es cero. Más precisamente, el flujo potencial no puede explicar el comportamiento de los flujos que incluyen una capa límite. Sin embargo, comprender el flujo potencial es importante en muchas ramas de la mecánica de fluidos. En particular, los flujos potenciales simples (llamados flujos elementales) como el vórtice libre y la fuente puntual poseen soluciones analíticas listas. Estas soluciones se pueden superponer para crear flujos más complejos que satisfagan una variedad de condiciones de contorno. Estos flujos se corresponden estrechamente con los flujos de la vida real en toda la mecánica de fluidos; además, surgen muchas ideas valiosas al considerar la desviación (a menudo leve) entre un flujo observado y el flujo potencial correspondiente. El flujo potencial encuentra muchas aplicaciones en campos como el diseño de aeronaves. Por ejemplo, en dinámica de fluidos computacional, una técnica es acoplar una solución de flujo potencial fuera de la capa límite a una solución de las ecuaciones de la capa límite dentro de la capa límite. La ausencia de efectos de capa límite significa que cualquier línea de corriente puede ser reemplazada por un límite sólido sin cambios en el campo de flujo, una técnica utilizada en muchos enfoques de diseño aerodinámico. Otra técnica sería el uso de sólidos de Riabouchinsky.

Análisis de flujo bidimensional

El flujo de potencial en dos dimensiones es simple de analizar utilizando mapeo conforme, mediante el uso de transformaciones del plano complejo. Sin embargo, no se requiere el uso de números complejos, como por ejemplo en el análisis clásico del flujo de fluidos que pasa por un cilindro. No es posible resolver un flujo potencial usando números complejos en tres dimensiones.

La idea básica es usar una función holomorfa (también llamada analítica) o meromórfica $f$ , que mapea el dominio físico $(x, y)$ al dominio transformado $(φ, ψ)$ . Mientras $x$ , $y$ , $φ$ y $ψ$ son todas de valor real, es conveniente definir las cantidades complejas

{displaystyle {begin{aligned}z&=x+iy,,{text{ and }}&w&=varphi +ipsi ,.end{aligned}}}

Ahora, si escribimos la asignación $f$ como

{displaystyle {begin{aligned}f(x+iy)&=varphi +ipsi ,,{text{ or }}&f(z)&=w,.end{aligned}}}

Entonces, debido a que $f$ es una función holomorfa o meromórfica, tiene que satisfacer las ecuaciones de Cauchy-Riemann

{displaystyle {begin{aligned}{frac {partial varphi }{partial x}}&={frac {partial psi }{partial y}},,&{frac {partial varphi }{partial y}}&=-{frac {partial psi }{partial x}},.end{aligned}}}

Los componentes de velocidad $(u, v)$ , en el $(x, y)$ respectivamente, se pueden obtener directamente de $f$ diferenciando con respecto a $z$ . Eso es

{displaystyle {frac {df}{dz}}=u-iv}

Entonces el campo de velocidad $v = (u, v)$ está especificado por

{displaystyle {begin{aligned}u&={frac {partial varphi }{partial x}}={frac {partial psi }{partial y}},&v&={frac {partial varphi }{partial y}}=-{frac {partial psi }{partial x}},.end{aligned}}}

Tanto $φ$ como $ψ$ luego satisfaga la ecuación de Laplace:

{displaystyle {begin{aligned}Delta varphi &={frac {partial ^{2}varphi }{partial x^{2}}}+{frac {partial ^{2}varphi }{partial y^{2}}}=0,,{text{ and }}&Delta psi &={frac {partial ^{2}psi }{partial x^{2}}}+{frac {partial ^{2}psi }{partial y^{2}}}=0,.end{aligned}}}

Entonces, $φ$ puede identificarse como el potencial de velocidad y $ψ$ se denomina función de flujo. Las líneas de constante $ψ$ se conocen como líneas aerodinámicas y las líneas de constante $φ$ se conocen como líneas equipotenciales (ver superficie equipotencial).

Las líneas de corriente y las líneas equipotenciales son ortogonales entre sí, ya que

{displaystyle nabla varphi cdot nabla psi ={frac {partial varphi }{partial x}}{frac {partial psi }{partial x}}+{frac {partial varphi }{partial y}}{frac {partial psi }{partial y}}={frac {partial psi }{partial y}}{frac {partial psi }{partial x}}-{frac {partial psi }{partial x}}{frac {partial psi }{partial y}}=0,.}

Así, el flujo se produce a lo largo de las líneas de la constante $ψ$ y en ángulo recto con las líneas de la constante $φ$ .

$Δ ψ = 0$ también se cumple, siendo esta relación equivalente a $\nabla \times v = 0$ . Entonces el flujo es irrotacional. La condición automática $\partial 2 Ψ / \partial x \partial y = \partial 2 Ψ / \partial y \partial x$ luego da la restricción de incompresibilidad $\nabla \cdot v = 0$ .

Ejemplos de flujos bidimensionales

Se puede usar cualquier función diferenciable para $f$ . Los ejemplos que siguen utilizan una variedad de funciones elementales; También se pueden utilizar funciones especiales. Tenga en cuenta que se pueden usar funciones de valores múltiples, como el logaritmo natural, pero la atención debe limitarse a una sola superficie de Riemann.

Leyes de potencia

Ejemplos de mapas conformados para la ley de poder

w = Az n

Ejemplos de mapas conformados para la ley de poder

w = Az n

, para diferentes valores del poder

n

. Shown es el

z

-plano, mostrando líneas de potencial constante

φ

y funcionamiento de la corriente

↑

, mientras

w = φ + i

En caso de que se aplique el siguiente mapa conforme de ley de potencia, de $z = x + iy$ a $w = φ + iψ$ :

{displaystyle w=Az^{n},,}

luego, escribiendo $z$ en coordenadas polares como $z = x + iy = re iθ$ , tenemos

{displaystyle varphi =Ar^{n}cos ntheta qquad {text{and}}qquad psi =Ar^{n}sin ntheta ,.}

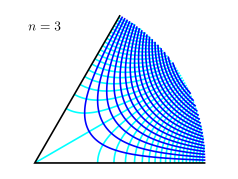
En las figuras de la derecha se dan ejemplos de varios valores de $n$ . La línea negra es el límite del flujo, mientras que las líneas azules más oscuras son líneas de corriente y las líneas azules más claras son líneas equipotenciales. Algunos poderes interesantes $n$ son:

$n = 1 / 2$ : esto corresponde con el flujo alrededor de una placa semi-infinita,
$n = 2 / 3$ : fluye alrededor de una esquina derecha,
$n = 1$ : un caso trivial de flujo uniforme,
$n = 2$ : fluir a través de una esquina, o cerca de un punto de estancamiento, y
$n = 1 -$ : flujo debido a una doble fuente

La constante $A$ es un parámetro de escala: su valor absoluto $| A |$ determina la escala, mientras que su argumento $arg(A)$ introduce una rotación (si no es cero).

Leyes de potencia con n = 1: flujo uniforme

Si $w = Az 1$ , es decir, una ley de potencia con $n = 1$ , las líneas de corriente (es decir, líneas de constante $ψ$ ) son un sistema de líneas rectas paralelas al eje $x$ . Esto es más fácil de ver escribiendo en términos de componentes reales e imaginarios:

{displaystyle f(x+iy)=A,(x+iy)=Ax+iAy}

dando así $φ = Ax$ y $ψ = Sí$ . Este flujo puede interpretarse como flujo uniforme paralelo al eje $x$ .

Leyes de potencia con n = 2

Si $n = 2$ , entonces $w = Az 2$ y la línea de corriente correspondiente a un valor particular de $ψ$ son aquellas puntos satisfactorios

{displaystyle psi =Ar^{2}sin 2theta ,,}

que es un sistema de hipérbolas rectangulares. Esto puede verse volviendo a escribir en términos de componentes reales e imaginarios. Observando que $sin 2θ = 2 sin θ cos θ$ y reescribiendo $sin θ = y / r$ y $cos θ = x / r$ se ve (al simplificar) que las líneas de corriente están dadas por

{displaystyle psi =2Axy,.}

El campo de velocidad viene dado por $\nabla φ$ , o

{displaystyle {begin{pmatrix}u\vend{pmatrix}}={begin{pmatrix}{frac {partial varphi }{partial x}}\[2px]{frac {partial varphi }{partial y}}end{pmatrix}}={begin{pmatrix}+{partial psi over partial y}\[2px]-{partial psi over partial x}end{pmatrix}}={begin{pmatrix}+2Ax\[2px]-2Ayend{pmatrix}},.}

En dinámica de fluidos, el campo de flujo cerca del origen corresponde a un punto de estancamiento. Tenga en cuenta que el fluido en el origen está en reposo (esto sigue a la diferenciación de $f (z) = z 2$ en $z = 0$ ). La línea de corriente $ψ = 0$ es particularmente interesante: tiene dos (o cuatro) ramas, siguiendo los ejes de coordenadas, es decir, <span class="texhtml" x = 0 y $y = 0$ . Como ningún fluido fluye a través del eje $x$ , (el $x$ -eje) puede tratarse como un límite sólido. Por lo tanto, es posible ignorar el flujo en el semiplano inferior donde $y < 0$ y centrarse en el flujo en el semiplano superior. Con esta interpretación, el flujo es el de un chorro dirigido verticalmente que incide sobre una placa plana horizontal. El flujo también puede interpretarse como flujo en una esquina de 90 grados si las regiones especificadas por (digamos) $x, y < 0$ se ignoran.

Leyes de potencia con n = 3

Si $n = 3$ , el flujo resultante es una especie de versión hexagonal del $n = 2$ caso considerado anteriormente. Las líneas de corriente están dadas por, $ψ = 3 x 2 y - y 3$ y el flujo en este caso puede interpretarse como flujo en una esquina de 60°.

Leyes de potencia con n = −1: doblete

Si $n = -1$ , las líneas de corriente están dadas por

{displaystyle psi =-{frac {A}{r}}sin theta.}

Esto se interpreta más fácilmente en términos de componentes reales e imaginarios:

{displaystyle {begin{aligned}psi ={frac {-Ay}{r^{2}}}&={frac {-Ay}{x^{2}+y^{2}}},,\x^{2}+y^{2}+{frac {Ay}{psi }}&=0,,\x^{2}+left(y+{frac {A}{2psi }}right)^{2}&=left({frac {A}{2psi }}right)^{2},.end{aligned}}}

Por lo tanto, las líneas de corriente son círculos que son tangentes al eje x en el origen. Los círculos en el semiplano superior fluyen así en el sentido de las agujas del reloj, los del semiplano inferior fluyen en el sentido contrario a las agujas del reloj. Tenga en cuenta que los componentes de velocidad son proporcionales a $r -2$ ; y sus valores en el origen es infinito. Este patrón de flujo generalmente se denomina doblete o dipolo, y se puede interpretar como la combinación de un par fuente-sumidero de fuerza infinita que se mantiene a una distancia infinitesimalmente pequeña.. El campo de velocidades está dado por

{displaystyle (u,v)=left({frac {partial psi }{partial y}},-{frac {partial psi }{partial x}}right)=left(A{frac {y^{2}-x^{2}}{left(x^{2}+y^{2}right)^{2}}},-A{frac {2xy}{left(x^{2}+y^{2}right)^{2}}}right),.}

o en coordenadas polares:

{displaystyle (u_{r},u_{theta })=left({frac {1}{r}}{frac {partial psi }{partial theta }},-{frac {partial psi }{partial r}}right)=left(-{frac {A}{r^{2}}}cos theta-{frac {A}{r^{2}}}sin theta right),.}

Leyes de potencia con n = −2: cuadrupolo

Si $n = -2$ , las líneas de corriente están dadas por

{displaystyle psi =-{frac {A}{r^{2}}}sin 2theta ,.}

Este es el campo de flujo asociado con un cuadrupolo.

Línea fuente y sumidero

Una fuente de línea o lavabo de fuerza $Q$ () $0}" xmlns="http://www.w3.org/1998/Math/MathML">Q■0{displaystyle Q0}0" aria-hidden="true" class="mwe-math-fallback-image-inline" src="https://wikimedia.org/api/rest_v1/media/math/render/svg/0ce6854254e374a59457fe11f86469e1a44c29f7" style="vertical-align: -0.671ex; width:6.099ex; height:2.509ex;"/>$ para fuente y $<math alttext="{displaystyle QQ.0{displaystyle Q 0} <img alt="{displaystyle Q$ para el sumidero) se da por el potencial

{displaystyle w={frac {Q}{2pi }}ln z}

Donde $Q$ de hecho es el flujo de volumen por longitud de unidad a través de una superficie que encierra la fuente o el fregadero. El campo de velocidad en coordenadas polares son

{displaystyle u_{r}={frac {Q}{2pi r}},quad u_{theta }=0}

es decir, un flujo puramente radial.

Vórtice de línea

Un vórtice de la línea de fuerza $Gamma$ es dado por

{displaystyle w={frac {Gamma }{2pi i}}ln z}

Donde $Gamma$ es la circulación alrededor de cualquier contorno cerrado simple que rodea el vórtice. El campo de velocidad en coordenadas polares son

{displaystyle u_{r}=0,quad u_{theta }={frac {Gamma }{2pi r}}}

es decir, un flujo puramente azimutal.

Análisis de flujo tridimensional

Para flujos tridimensionales, no se puede obtener el potencial complejo.

Fuente puntual y sumidero

El potencial de velocidad de una fuente de punto o el hundimiento de la fuerza $Q$ () $0}" xmlns="http://www.w3.org/1998/Math/MathML">Q■0{displaystyle Q0}0" aria-hidden="true" class="mwe-math-fallback-image-inline" src="https://wikimedia.org/api/rest_v1/media/math/render/svg/0ce6854254e374a59457fe11f86469e1a44c29f7" style="vertical-align: -0.671ex; width:6.099ex; height:2.509ex;"/>$ para fuente y $<math alttext="{displaystyle QQ.0{displaystyle Q 0} <img alt="{displaystyle Q$ para hundir) en coordenadas polares esféricas es dada por

{displaystyle phi =-{frac {Q}{4pi r}}}

Donde $Q$ de hecho es el flujo de volumen a través de una superficie cerrada que encierra la fuente o el fregadero. El campo de velocidad en las coordenadas polares esféricas son

{displaystyle u_{r}={frac {Q}{4pi r^{2}}},quad u_{theta }=0,quad u_{phi }=0.}

Contenido relacionado

Más resultados...