Filtro de paso bajo

Un filtro de paso bajo es un filtro que deja pasar señales con una frecuencia inferior a la frecuencia de corte seleccionada y atenúa las señales con frecuencias superiores a la frecuencia de corte. La respuesta de frecuencia exacta del filtro depende del diseño del filtro. El filtro a veces se denomina filtro de corte de agudos o filtro de corte de agudos en aplicaciones de audio. Un filtro de paso bajo es el complemento de un filtro de paso alto.

En óptica, paso alto y paso bajo pueden tener diferentes significados, según se trate de la frecuencia o de la longitud de onda de la luz, ya que estas variables están inversamente relacionadas. Los filtros de frecuencia de paso alto actuarían como filtros de longitud de onda de paso bajo y viceversa. Por esta razón, es una buena práctica referirse a los filtros de longitud de onda como paso corto y paso largo para evitar confusiones, lo que correspondería a paso alto< /i> y frecuencias de paso bajo.

Los filtros de paso bajo existen en muchas formas diferentes, incluidos circuitos electrónicos como un filtro de silbido utilizado en audio, filtros antisolapamiento para acondicionar señales antes de la conversión de analógico a digital, filtros digitales para suavizar conjuntos de datos, barreras acústicas, desenfoque de imágenes, etc. La operación de promedio móvil utilizada en campos como las finanzas es un tipo particular de filtro de paso bajo y se puede analizar con las mismas técnicas de procesamiento de señales que se usan para otros filtros de paso bajo. Los filtros de paso bajo proporcionan una forma más suave de señal, eliminando las fluctuaciones a corto plazo y dejando la tendencia a largo plazo.

Los diseñadores de filtros suelen utilizar el formulario de paso bajo como prototipo de filtro. Es decir, un filtro con ancho de banda e impedancia unidad. El filtro deseado se obtiene del prototipo escalando para el ancho de banda y la impedancia deseados y transformándolo en la forma de banda deseada (es decir, paso bajo, paso alto, paso de banda o supresión de banda).

Ejemplos

Los ejemplos de filtros de paso bajo ocurren en acústica, óptica y electrónica.

Una barrera física rígida tiende a reflejar frecuencias de sonido más altas y, por lo tanto, actúa como un filtro acústico de paso bajo para transmitir el sonido. Cuando se reproduce música en otra habitación, las notas bajas se escuchan fácilmente, mientras que las notas altas se atenúan.

Un filtro óptico con la misma función puede denominarse correctamente filtro de paso bajo, pero convencionalmente se denomina filtro paso largo (la frecuencia baja es una longitud de onda larga), para evitar confusiones.

En un filtro RC de paso bajo electrónico para señales de voltaje, las frecuencias altas en la señal de entrada se atenúan, pero el filtro tiene poca atenuación por debajo de la frecuencia de corte determinada por su constante de tiempo RC. Para las señales de corriente, un circuito similar, que usa una resistencia y un capacitor en paralelo, funciona de manera similar. (Vea el divisor actual discutido con más detalle a continuación).

Los filtros de paso bajo electrónicos se utilizan en las entradas de los subwoofers y otros tipos de altavoces para bloquear los tonos altos que no pueden reproducir de manera eficiente. Los transmisores de radio usan filtros de paso bajo para bloquear las emisiones armónicas que podrían interferir con otras comunicaciones. La perilla de tono en muchas guitarras eléctricas es un filtro de paso bajo que se usa para reducir la cantidad de agudos en el sonido. Un integrador es otro filtro de paso bajo constante en el tiempo.

Las líneas telefónicas equipadas con divisores DSL utilizan filtros de paso bajo y paso alto para separar las señales DSL y POTS que comparten el mismo par de cables.

Los filtros de paso bajo también juegan un papel importante en la escultura del sonido creado por sintetizadores analógicos y analógicos virtuales. Ver síntesis sustractiva.

Se utiliza un filtro de paso bajo como filtro antisolapamiento antes del muestreo y para la reconstrucción en la conversión de digital a analógico.

Filtros ideales y reales

La función sinc, la respuesta del impulso de tiempo-dominio de un filtro de paso bajo ideal.

La respuesta de frecuencia de ganancia-magnitud de un filtro de paso bajo de primer orden (una capa). Ganancia de energía se muestra en decibeles (es decir, una disminución de 3 dB refleja una atenuación adicional de media potencia). La frecuencia angular se muestra en una escala logarítmica en unidades de radians por segundo.

Un filtro de paso bajo ideal elimina por completo todas las frecuencias por encima de la frecuencia de corte y deja pasar las que están por debajo sin cambios; su respuesta de frecuencia es una función rectangular y es un filtro de pared de ladrillo. La región de transición presente en los filtros prácticos no existe en un filtro ideal. Un filtro de paso bajo ideal se puede realizar matemáticamente (teóricamente) multiplicando una señal por la función rectangular en el dominio de la frecuencia o, de manera equivalente, la convolución con su respuesta de impulso, una función sinc, en el dominio del tiempo.

Sin embargo, el filtro ideal es imposible de realizar sin tener también señales de una extensión infinita en el tiempo y, por lo general, debe aproximarse a las señales reales en curso, porque la región de soporte de la función sinc se extiende a todo el pasado y el futuro. veces. Por lo tanto, el filtro necesitaría tener una demora infinita, o conocimiento del futuro y el pasado infinitos, para realizar la convolución. Es efectivamente realizable para señales digitales pregrabadas asumiendo extensiones de cero en el pasado y el futuro, o más típicamente haciendo que la señal sea repetitiva y usando el análisis de Fourier.

Los filtros reales para aplicaciones en tiempo real se aproximan al filtro ideal al truncar y aplicar ventanas a la respuesta de impulso infinita para crear una respuesta de impulso finita; aplicar ese filtro requiere retrasar la señal durante un período de tiempo moderado, lo que permite que el cálculo "vea" un poco hacia el futuro. Este retraso se manifiesta como cambio de fase. Una mayor precisión en la aproximación requiere un retraso mayor.

Un filtro de paso bajo ideal da como resultado artefactos de timbre a través del fenómeno de Gibbs. Estos pueden reducirse o empeorarse mediante la elección de la función de ventana, y el diseño y la elección de filtros reales implica comprender y minimizar estos artefactos. Por ejemplo, "simple truncamiento [de sinc] causa graves artefactos de timbre," en la reconstrucción de la señal, y para reducir estos artefactos, se utilizan funciones de ventana "que caen más suavemente en los bordes".

La fórmula de interpolación de Whittaker-Shannon describe cómo usar un filtro de paso bajo perfecto para reconstruir una señal continua a partir de una señal digital muestreada. Los convertidores reales de digital a analógico utilizan aproximaciones de filtros reales.

Respuesta de tiempo

La respuesta temporal de un filtro de paso bajo se encuentra resolviendo la respuesta del filtro RC de paso bajo simple.

Un simple filtro RC de paso bajo

Usando la Ley de Kirchhoff llegamos a la ecuación diferencial

${displaystyle v_{out}(t)=v_{text{in}(t)-RC{frac {operatorname {d} v_{text{out}} {}{operatorname {d} t}}}} {f}}} {f}}} {f}}}}} {f}}}}}}}} {$

Ejemplo de respuesta de entrada de paso

Si lo dejamos ${displaystyle v_{in}(t)}$ ser una función paso de magnitud ${displaystyle V_{i}$ entonces la ecuación diferencial tiene la solución

${displaystyle v_{out}(t)=V_{i}(1-e^{-omega _{0}t}),}$

Donde ${displaystyle omega _{0}={1 over RC}$ es la frecuencia de corte del filtro.

Respuesta de frecuencia

La forma más común de caracterizar la respuesta de frecuencia de un circuito es encontrar su función de transferencia de transformación de Laplace, ${displaystyle H(s)={rm {out}(s) over V_{rm {in}(s)}}}$. Tomar la transformación de Laplace de nuestra ecuación diferencial y resolver para ${displaystyle H(s)}$ nosotros

${displaystyle H(s)={V_{rm {out}(s) over V_{rm {in}(s)}={omega ¿Qué?$

Ecuación de diferencia mediante muestreo en tiempo discreto

Una ecuación de diferencia discreta se obtiene fácilmente mediante el muestreo de la respuesta de entrada paso arriba a intervalos regulares de ${displaystyle nT}$ Donde ${displaystyle n=0,1,...}$ y ${displaystyle T}$ es el momento entre las muestras. Tomando la diferencia entre dos muestras consecutivas que tenemos

${displaystyle v_{rm {}(nT)-v_{rm {}(n-1)T)=V_{i}(1-e^{-omega ¿Por qué?$

Solving for ${displaystyle v_{rm {}(nT)}$ nosotros

${displaystyle v_{rm {}(nT)=beta v_{rm {out}(n-1)T)+(1-beta)V_{i}}$

Donde ${displaystyle beta =e^{-omega ¿Qué?$

Usando la notación ${displaystyle V_{n}=v_{rm {out}(nT)}$ y ${displaystyle ¿Qué?$, y sustitución de nuestro valor muestrado, ${displaystyle ¿Qué?$, tenemos la ecuación de la diferencia

${displaystyle V_{n}=beta V_{n-1}+(1-beta)v_{n}$

Análisis de errores

Comparando la señal de salida reconstruida de la ecuación de diferencia, ${displaystyle V_{n}=beta V_{n-1}+(1-beta)v_{n}$, a la respuesta de la entrada paso, ${displaystyle v_{out}(t)=V_{i}(1-e^{-omega _{0}t})}$, encontramos que hay una reconstrucción exacta (0% error). Esta es la salida reconstruida para una entrada invariante de tiempo. Sin embargo, si la entrada es tiempo variante, como ${displaystyle v_{in}(t)=V_{i}sin(omega t)}$, este modelo aproxima la señal de entrada como una serie de funciones de paso con duración ${displaystyle T}$ produciendo un error en la señal de salida reconstruida. El error producido tiempo variante los insumos es difícil cuantificar pero disminuye como ${displaystyle Trightarrow 0}$.

Realización en tiempo discreto

Muchos filtros digitales están diseñados para brindar características de paso bajo. Tanto los filtros de paso bajo de respuesta de impulso infinito como los filtros de paso bajo de respuesta de impulso finito, así como los filtros que utilizan transformadas de Fourier, son ampliamente utilizados.

Filtro de respuesta de impulso infinito simple

El efecto de un filtro de paso bajo de respuesta de impulso infinito se puede simular en una computadora analizando el comportamiento de un filtro RC en el dominio del tiempo y luego discretizando el modelo.

Un simple filtro RC de paso bajo

Del diagrama del circuito a la derecha, según las Leyes de Kirchhoff y la definición de capacitancia:

${displaystyle v_{in}(t)-v_{out}(t)=R;i(t)}$

()V)

${displaystyle Q_{c}(t)=C,v_{text{out}(t)}$

()Q)

${displaystyle i(t)={frac {operatorname {} {fn} {fnK}} {fnK}} {f}}}} {fn}} {fn}}}}} {fn} {f}}}}}} {fn}}}}}}}}} {f}}}} {f}}}} {f}}}}}}}}}}}}}}}}}}}}} {}}}}}}}}} {}}}}}}}}}}}}}}}}}}}}}} {}}}}}}}}}}}}}}}}}}}}}} {\\\\\\\\\\\\f}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}$

()I)

Donde ${displaystyle Q_{c}(t)}$ es la carga almacenada en el condensador a tiempo t. Ecuación sustitutiva Q en la ecuación I da ${displaystyle i(t);=;C{frac {fnh} {fnh} {\fnh}} {fnh}}} {\fn}}}} {fn}}} {fnK}}}} {fnf}}}}}$, que se puede sustituir en la ecuación V así

${displaystyle v_{text{in}(t)-v_{text{out}(t)=RC{frac {operatorname {d} v_{text{out}}{operatorname {d} t}}$

Esta ecuación puede ser discretizada. Para la simplicidad, asuma que las muestras de la entrada y la salida se toman en puntos uniformemente espaciados en el tiempo separados por ${displaystyle Delta _{T}$ tiempo. Dejar las muestras de ${displaystyle ¿Qué?$ ser representado por la secuencia ${fnMicrosoft Sans Serif}$, y dejar ${displaystyle v_{text{out}}$ ser representado por la secuencia ${fnMicrosoft Sans Serif}$, que corresponden a los mismos puntos en el tiempo. Haciendo estas sustituciones,

${displaystyle ¿Qué? {y_{i}-y_{i-1}{ Delta - Sí.$

Reordenar los términos da la relación de recurrencia

${displaystyle Y... {Delta _{T}{RC+Delta - Sí. ^{text{Input contribution}}+overbrace {y_{i-1}left({frac {RC}{RC+Delta _{T}}}right)} ^{text{Inertia de la salida anterior}}$

Es decir, esta implementación en tiempo discreto de un filtro de paso bajo RC simple es el promedio móvil ponderado exponencialmente

${displaystyle Y... x_{i}+(1-alpha)y_{i-1}qquad {text{where}qquad alpha:={frac {Delta {T}{RC+Delta - Sí.$

Por definición, la factor suavizado está dentro del rango ${displaystyle 0;leq ;alpha ;leq ;1}$. La expresión α cede el tiempo equivalente constante RC en términos del período de muestreo ${displaystyle Delta _{T}$ y factor de suavidad α,

${displaystyle RC=Delta _{T}left({frac {1-alpha }{alpha }}right). }$

Recordando eso

${displaystyle F_{c}={frac {1}{2pi} RC}$ Así que... ${displaystyle RC={frac}{2pi}.$

nota α y ${displaystyle f_{c}$ están relacionados por,

${displaystyle alpha ={frac {2piDelta {f} {f}{2} Delta ¿Qué?$

y

${displaystyle f_{c}={frac {alpha }{(1-alpha)2pi Delta _{T}}}}$

Si α=0.5, entonces el RC tiempo constante es igual al período de muestreo. Si ${displaystyle alpha ;ll;0.5}$, entonces RC es significativamente mayor que el intervalo de muestreo, y ${displaystyle Delta _{T};approx ;alpha RC}$.

La relación de recurrencia del filtro proporciona una forma de determinar las muestras de salida en términos de las muestras de entrada y la salida anterior. El siguiente algoritmo de pseudocódigo simula el efecto de un filtro de paso bajo en una serie de muestras digitales:

// Regresar muestras de salida de filtros de baja velocidad RC, muestras de entrada dadas,
// intervalo de tiempo ♪, y tiempo constante RCfunción lowpass(real[1..n] x, real dt, real RC)
 Var real[1..n] Sí.
 Var real α:= dt / (RC + dt)
y[1]:= α * x[1]
 para i desde 2 a n
y[i]:= α * x[i] + (1-α) * y[i-1]
 retorno Sí.

El bucle que calcula cada una de las salidas n se puede refactorizar en el equivalente:

 para i desde 2 a n
y[i]:= y[i-1] + α * (x[i] - y[i-1])

Es decir, el cambio de una salida de filtro a la siguiente es proporcional a la diferencia entre la salida anterior y la siguiente entrada. Esta propiedad de licuado exponencial coincide con la decadencia exponencial vista en el sistema de tiempo continuo. Como se esperaba, como el tiempo constante RC aumenta, el parámetro de suavizado de tiempo discreto ${displaystyle alpha }$ disminuciones, y las muestras de salida ${fnMicrosoft Sans Serif}$ responder más lentamente a un cambio en las muestras de entrada ${fnMicrosoft Sans Serif}$; el sistema tiene más inercia. Este filtro es un filtro de bajo paso de una sola capa (IIR).

Respuesta de impulso finito

Se pueden construir filtros de respuesta de impulso finito que se aproximen a la respuesta en el dominio del tiempo de la función sinc de un filtro ideal de paso bajo de corte nítido. Para una distorsión mínima, el filtro de respuesta de impulso finito tiene un número ilimitado de coeficientes que operan en una señal ilimitada. En la práctica, la respuesta en el dominio del tiempo debe ser truncada en el tiempo y, a menudo, tiene una forma simplificada; en el caso más simple, se puede usar un promedio móvil, dando una respuesta de tiempo al cuadrado.

Transformada de Fourier

Para el filtrado que no es en tiempo real, para lograr un filtro de paso bajo, la señal completa generalmente se toma como una señal en bucle, se toma la transformada de Fourier, se filtra en el dominio de la frecuencia, seguida de una transformada de Fourier inversa. Solo se requieren operaciones O(n log(n)) en comparación con O(n²) para el algoritmo de filtrado en el dominio del tiempo.

A veces, esto también se puede hacer en tiempo real, donde la señal se retrasa lo suficiente como para realizar la transformación de Fourier en bloques superpuestos más cortos.

Realización en tiempo continuo

Parcela de la ganancia de filtros de paso bajo Butterworth de pedidos 1 a 5, con frecuencia de corte ${displaystyle omega ¿Qué?$. Tenga en cuenta que la pendiente es 20n dB/decade n es la orden de filtro.

Hay muchos tipos diferentes de circuitos de filtro, con diferentes respuestas a los cambios de frecuencia. La respuesta de frecuencia de un filtro generalmente se representa mediante un diagrama de Bode, y el filtro se caracteriza por su frecuencia de corte y la tasa de caída de frecuencia. En todos los casos, a la frecuencia de corte, el filtro atenúa la potencia de entrada a la mitad o 3 dB. Entonces, el orden del filtro determina la cantidad de atenuación adicional para frecuencias más altas que la frecuencia de corte.

• A filtro de primer orden, por ejemplo, reduce la amplitud de la señal a la mitad (así que la energía disminuye por un factor de 4, o 6 dB), cada vez que la frecuencia se duplica (va por encima de una octava); más precisamente, el flujo de energía se acerca 20 dB por decenio en el límite de alta frecuencia. El diagrama Bode de magnitud para un filtro de primer orden parece una línea horizontal por debajo de la frecuencia de corte, y una línea diagonal por encima de la frecuencia de corte. También hay una " curva de rodilla" en el límite entre los dos, que transiciones suavemente entre las dos regiones de línea recta. Si la función de transferencia de un filtro de paso bajo de primer orden tiene un cero, así como un polo, el diagrama Bode se aplana de nuevo, a alguna atenuación máxima de frecuencias altas; tal efecto es causado por ejemplo por un poco de la entrada que se filtra alrededor del filtro de una sola capa; este filtro de una sola capa – una cero sigue siendo un filtro de baja velocidad de primer orden. Ver diagrama Pole-cero y circuito RC.
• A filtro de segunda orden atenua las frecuencias altas más abruptamente. La trama Bode para este tipo de filtro se asemeja a la de un filtro de primer orden, excepto que se cae más rápidamente. Por ejemplo, un filtro Butterworth de segunda orden reduce la amplitud de señal a un cuarto su nivel original cada vez que la frecuencia se duplica (así que la potencia disminuye en 12 dB por octava, o 40 dB por década). Otros filtros de segundo orden de pólvora de pólvora pueden bajar a diferentes tarifas inicialmente dependiendo de su factor Q, pero acercarse a la misma tasa final de 12 dB por octava; como con los filtros de primer orden, los ceros en la función de transferencia pueden cambiar el asintoto de alta frecuencia. Vea el circuito RLC.
• Los filtros de orden tercero y superior se definen de forma similar. En general, la tasa final de derrame de energía para un orden- n filtro de toda la capa es 6n dB por octava (20n dB por decenio).

En cualquier filtro Butterworth, si uno extiende la línea horizontal hacia la derecha y la línea diagonal hacia la parte superior izquierda (las asíntotas de la función), se cruzan exactamente en la frecuencia de corte, 3 dB por debajo de la línea horizontal. Los diversos tipos de filtros (filtro Butterworth, filtro Chebyshev, filtro Bessel, etc.) tienen curvas de rodilla de aspecto diferente. Muchos filtros de segundo orden tienen "picos" o resonancia que pone su respuesta de frecuencia por encima de la línea horizontal en este pico.

Los significados de 'bajo' y 'alta', es decir, la frecuencia de corte, dependen de las características del filtro. El término "filtro de paso bajo" simplemente se refiere a la forma de la respuesta del filtro; se podría construir un filtro de paso alto que corte a una frecuencia más baja que cualquier filtro de paso bajo: son sus respuestas las que los diferencian. Los circuitos electrónicos se pueden diseñar para cualquier rango de frecuencia deseado, hasta frecuencias de microondas (por encima de 1 GHz) y superiores.

Notación de Laplace

Los filtros de tiempo continuo también se pueden describir en términos de la transformada de Laplace de su respuesta de impulso, de una manera que permite analizar fácilmente todas las características del filtro considerando el patrón de polos y ceros de la transformada de Laplace en el complejo avión. (En tiempo discreto, se puede considerar de manera similar la transformada Z de la respuesta al impulso).

Por ejemplo, un filtro de paso bajo de primer orden se puede describir en notación de Laplace como:

${displaystyle {frac {text{Output}{text{Input}=K{frac} {1}{tau s+1}}$

donde s es la variable de transformada de Laplace, τ es la constante de tiempo del filtro y K es la ganancia del filtro en la banda de paso.

Filtros electrónicos de paso bajo

Primer pedido

Filtro RC

Filtro RC pasivo, primer orden

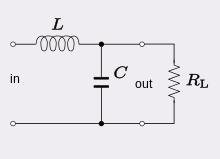
Un simple circuito de filtro de baja velocidad consiste en un resistor en serie con una carga, y un condensador en paralelo con la carga. El condensador exhibe la reacción, y bloquea las señales de baja frecuencia, forzándolas a través de la carga en su lugar. A frecuencias más altas la reacción cae, y el condensador funciona eficazmente como un cortocircuito. La combinación de resistencia y capacitancia da la constante del tiempo del filtro ${displaystyle tau ;=;RC}$ (representado por la carta griega tau). La frecuencia de rotura, también llamada frecuencia de rotación, frecuencia de esquina o frecuencia de corte (en hertz), se determina por la constante de tiempo:

${displaystyle f_{mathrm {c}={1over 2pitau }={1over 2pi} RC}$

o equivalente (en radianes por segundo):

${displaystyle omega _{mathrm {c}={1 over tau }={1 over RC}$

Este circuito puede entenderse considerando el tiempo que necesita el capacitor para cargarse o descargarse a través de la resistencia:

• En frecuencias bajas, hay mucho tiempo para que el condensador cargue hasta prácticamente el mismo voltaje que el voltaje de entrada.
• En frecuencias altas, el condensador sólo tiene tiempo para cargar una pequeña cantidad antes de la dirección de interruptores de entrada. La salida sube y baja sólo una pequeña fracción de la cantidad que la entrada va arriba y abajo. Al doble de la frecuencia, sólo hay tiempo para que cobre la mitad de la cantidad.

Otra forma de entender este circuito es a través del concepto de reactancia a una determinada frecuencia:

• Puesto que la corriente directa (DC) no puede fluir a través del condensador, la entrada DC debe fluir por el camino marcado ${displaystyle V_{mathrm}}$ (análogo para eliminar el condensador).
• Puesto que la corriente alterna (AC) fluye muy bien a través del condensador, casi así como fluye a través de alambre sólido, la entrada de AC fluye hacia fuera a través del condensador, efectivamente cortocircuito a tierra (analógico para reemplazar el condensador con sólo un alambre).

El capacitor no es un "encendido/apagado" objeto (como el bloque o pasar la explicación fluídica anterior). El condensador actúa de forma variable entre estos dos extremos. Es el diagrama de Bode y la respuesta de frecuencia los que muestran esta variabilidad.

Filtro RL

Un circuito de resistencia-inductor o filtro RL es un circuito eléctrico compuesto de resistencias e inductores accionados por una fuente de voltaje o corriente. Un circuito RL de primer orden se compone de una resistencia y un inductor y es el tipo más simple de circuito RL.

Un circuito RL de primer orden es uno de los filtros electrónicos analógicos de respuesta de impulso infinito más simples. Consiste en una resistencia y un inductor, ya sea en serie impulsados por una fuente de voltaje o en paralelo impulsados por una fuente de corriente.

Segunda orden

(feminine)

Filtro RLC

Circuito RLC como filtro de paso bajo

Un circuito RLC (las letras R, L y C pueden estar en una secuencia diferente) es un circuito eléctrico que consta de una resistencia, un inductor y un condensador, conectados en serie o en paralelo. La parte RLC del nombre se debe a que esas letras son los símbolos eléctricos habituales de resistencia, inductancia y capacitancia, respectivamente. El circuito forma un oscilador armónico para la corriente y resonará de manera similar a como lo hará un circuito LC. La principal diferencia que hace la presencia de la resistencia es que cualquier oscilación inducida en el circuito desaparecerá con el tiempo si una fuente no la mantiene. Este efecto de la resistencia se llama amortiguamiento. La presencia de la resistencia también reduce un poco la frecuencia de resonancia máxima. Cierta resistencia es inevitable en los circuitos reales, incluso si una resistencia no se incluye específicamente como componente. Un circuito LC puro ideal es una abstracción a los efectos de la teoría.

Hay muchas aplicaciones para este circuito. Se utilizan en muchos tipos diferentes de circuitos osciladores. Otra aplicación importante es la sintonización, como en los receptores de radio o televisores, donde se utilizan para seleccionar un rango estrecho de frecuencias de las ondas de radio ambientales. En esta función, el circuito a menudo se denomina circuito sintonizado. Un circuito RLC se puede utilizar como filtro de paso de banda, filtro de parada de banda, filtro de paso bajo o filtro de paso alto. El filtro RLC se describe como un circuito de segundo orden, lo que significa que cualquier voltaje o corriente en el circuito puede describirse mediante una ecuación diferencial de segundo orden en el análisis de circuitos.

Filtros pasivos de orden superior

También se pueden construir filtros pasivos de orden superior (consulte el diagrama para ver un ejemplo de tercer orden).

Un filtro de paso bajo de tercera orden (topología Cauer). El filtro se convierte en un filtro Butterworth con frecuencia de corte ω_c=1 cuando (por ejemplo) C₂=4/3 farad, R₄=1 ohm, L₁=3/2 henry y L₃= 1/2 henry.

Realización electrónica activa

Un filtro activo de baja velocidad

Otro tipo de circuito eléctrico es un filtro de paso bajo activo.

En el circuito del amplificador operacional que se muestra en la figura, la frecuencia de corte (en hercios) se define como:

${displaystyle F_{text{c}={1}{2pi} R_{2}C}}$

o equivalente (en radianes por segundo):

${displaystyle omega _{c}={frac} {1}{2}C}}$

La ganancia en la banda de paso es −R₂/R₁, y la banda de parada cae en −6 dB por octava (es decir −20 dB por década) ya que es un filtro de primer orden.