Filtro Chebyshev

Los filtros Chebyshev son filtros analógicos o digitales que tienen una atenuación más pronunciada que los filtros Butterworth y tienen ondulación de banda de paso (tipo I) o ondulación de banda suprimida (tipo II). Los filtros Chebyshev tienen la propiedad de minimizar el error entre la característica de filtro ideal y la real en el rango de frecuencia de funcionamiento del filtro, pero logran esto con ondas en la banda de paso. Este tipo de filtro lleva el nombre de Pafnuty Chebyshev porque sus características matemáticas se derivan de los polinomios de Chebyshev. Los filtros Chebyshev de tipo I suelen denominarse "filtros Chebyshev", mientras que los filtros de tipo II suelen denominarse "filtros Chebyshev inversos". Debido a la ondulación de la banda de paso inherente a los filtros Chebyshev, para ciertas aplicaciones se prefieren los filtros con una respuesta más suave en la banda de paso pero una respuesta más irregular en la banda suprimida.

Filtros tipo I Chebyshev (filtros Chebyshev)

Tipo I Los filtros Chebyshev son los tipos más comunes de filtros Chebyshev. La respuesta de ganancia (o amplitud) Gn()⋅ ⋅ ){displaystyle G_{n}(omega)}, como función de frecuencia angular ⋅ ⋅ {displaystyle omega } de la n{displaystyle n}filtro de paso bajo es igual al valor absoluto de la función de transferencia Hn()s){displaystyle H_{n}(s)} evaluados s=j⋅ ⋅ {displaystyle s=jomega }:

Gn()⋅ ⋅ )=SilencioHn()j⋅ ⋅ )Silencio=11+ε ε 2Tn2()⋅ ⋅ /⋅ ⋅ 0){displaystyle G_{n}(omega)=left sometidaH_{n}(jomega)right WordPress={frac {1}{sqrt {1+varepsilon ^{2}T_{n}{2}(omega /omega _{0}}}}}}}}}}}}}}}}

Donde ε ε {displaystyle varepsilon } es el factor de onda, ⋅ ⋅ 0{displaystyle omega ¿Qué? es la frecuencia de corte y Tn{displaystyle T_{n} es un polinomio Chebyshev del n{displaystyle n}orden.

La banda pasada exhibe comportamiento equiripple, con la onda determinada por el factor de onda ε ε {displaystyle varepsilon }. En la banda pasada, el polinomio Chebyshev alterna entre -1 y 1 por lo que el filtro ganar alterna entre maxima a G=1{displaystyle G=1} y minima en G=1/1+ε ε 2{displaystyle G=1/{sqrt {1+varepsilon ^{2}}.

Did you mean:

The ripple factor ε is this related to the passband ripple δ in decibels by:

ε ε =10δ δ /10− − 1.{displaystyle varepsilon ={sqrt {10^{delta - Sí.

En la frecuencia de corte ⋅ ⋅ 0{displaystyle omega ¿Qué? la ganancia de nuevo tiene el valor 1/1+ε ε 2{displaystyle 1/{sqrt {1+varepsilon }}}} pero sigue bajando en la banda de parada a medida que aumenta la frecuencia. Este comportamiento se muestra en el diagrama de la derecha. La práctica común de definir la frecuencia de corte a −3 dB generalmente no se aplica a los filtros de Chebyshev; en lugar de ello, el corte se toma como el punto en que la ganancia cae al valor de la onda para el tiempo final.

La frecuencia 3 dB ⋅ ⋅ H{displaystyle omega _{H} está relacionado con ⋅ ⋅ 0{displaystyle omega ¿Qué? por:

⋅ ⋅ H=⋅ ⋅ 0cosh⁡ ⁡ ()1ncosh− − 1⁡ ⁡ 1ε ε ).{displaystyle omega ### {H}=omega ¿Qué? {1} {varepsilon }derecha). }

El orden de un filtro Chebyshev es igual a la cantidad de componentes reactivos (por ejemplo, inductores) necesarios para realizar el filtro usando electrónica analógica.

Se puede obtener un rodillo aún más empinado si se permite la onda en la banda de parada, permitiendo ceros en la ⋅ ⋅ {displaystyle omega }-eje en el plano complejo. Si bien esto produce una supresión casi infinita en estos ceros (limitada por el factor de calidad de los componentes, parasitarios y factores conexos), la supresión general en la banda de parada se reduce. El resultado se llama filtro elíptico, también conocido como filtro Cauer.

Showing translation for

Poles and zeros

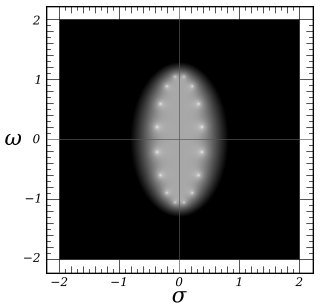
Para la simplicidad, se supone que la frecuencia de corte es igual a la unidad. Los polos ()⋅ ⋅ pm){displaystyle (omega _{pm})} de la función de ganancia del filtro Chebyshev son los ceros del denominador de la función de ganancia. Usando la frecuencia compleja s{displaystyle s}, estos ocurren cuando:

1+ε ε 2Tn2()− − js)=0.{displaystyle 1+varepsilon ^{2}T_{n}(-js)=0.,}

Definición − − js=#⁡ ⁡ ()Silencio Silencio ){displaystyle -js=cos(theta)} y el uso de la definición trigonométrica de los polinomios Chebyshev rinde:

1+ε ε 2Tn2()#⁡ ⁡ ()Silencio Silencio ))=1+ε ε 2#2⁡ ⁡ ()nSilencio Silencio )=0.{displaystyle 1+varepsilon ^{2}T_{2}(cos(theta)=1+varepsilon ^{2}cos ^{2}(ntheta)=0.}

Solving for Silencio Silencio {displaystyle theta }

Silencio Silencio =1narccos⁡ ⁡ ()± ± jε ε )+mπ π n{displaystyle theta ={frac {1}{n}}arccos left({frac {pm j}{varepsilon }}right)+{frac {mpi } {n}}

donde los múltiples valores de la función arc cosine se hacen explícitamente utilizando el índice entero m{displaystyle m}. Los polos de la función de ganancia Chebyshev son entonces:

spm=j#⁡ ⁡ ()Silencio Silencio ){displaystyle s_{pm}=jcos(theta),}

=j#⁡ ⁡ ()1narccos⁡ ⁡ ()± ± jε ε )+mπ π n).{displaystyle =jcos left({frac {1}{n}arccos left({frac {pm j}{varepsilon }}}right)+{frac {mpi }{n}right).}}}}}}}

Usando las propiedades de las funciones trigonométricas e hiperbólicas, esto puede escribirse en forma explícitamente compleja:

spm± ± =± ± pecado⁡ ⁡ ()1narsinh()1ε ε ))pecado⁡ ⁡ ()Silencio Silencio m){displaystyle s_{pm}{pm }=pm sinh left({frac {1}{n}mathrm {arsinh} left({frac {1}{varepsilon }right)derecha)sin(theta _{m}}}}}}}}}}}}}derech)dere)dere)dere)derech]derech]dere)dere)dere)derech]dere]

+jcosh⁡ ⁡ ()1narsinh()1ε ε ))#⁡ ⁡ ()Silencio Silencio m){displaystyle +jcosh left({frac {1}{n}mathrm {arsinh} left({frac {1}{varepsilon }right)cos(theta _{m}}}}}} {derecha)derecha)derecha)derecha)cos(theta]

Donde m=1,2,...,n{displaystyle m=1,2,...,n}y

Silencio Silencio m=π π 22m− − 1n.{displaystyle theta ¿Qué? {2m-1} {n}}}

Esto puede ser visto como una ecuación paramétrica en Silencio Silencio n{displaystyle theta _{n} y demuestra que los polos se encuentran en un elipse s{displaystyle s}- espacio centrado en s=0{displaystyle s=0} con un semi-eje real de longitud pecado⁡ ⁡ ()arsinh()1/ε ε )/n){displaystyle sinh(mathrm {arsinh} (1/varepsilon)/n)} y un semi-eje imaginario de longitud cosh⁡ ⁡ ()arsinh()1/ε ε )/n).{displaystyle cosh(mathrm {arsinh} (1/varepsilon)/n). }

La función de transferencia

La expresión anterior produce los polos de la ganancia G{displaystyle G.. Para cada polo complejo, hay otro que es el complejo conjugado, y para cada par conjugado hay dos más que son los negativos del par. La función de transferencia debe ser estable, por lo que sus polos son los de la ganancia que tienen partes reales negativas y por lo tanto se encuentran en el medio plano izquierdo del espacio de frecuencia compleja. La función de transferencia es entonces dada por

H()s)=12n− − 1ε ε ∏ ∏ m=1n1()s− − spm− − ){displaystyle H(s)={1}{2^{n-1}varepsilon }\prod _{m=1}{n}{n}{frac {1} {} {}}}}

Donde spm− − {displaystyle S_{pm} {} {} son sólo los polos de la ganancia con un signo negativo delante del término real, obtenido de la ecuación anterior.

El retraso del grupo

El retardo de grupo se define como la derivada de la fase con respecto a la frecuencia angular y es una medida de la distorsión en la señal introducida por diferencias de fase para diferentes frecuencias.

τ τ g=− − dd⋅ ⋅ arg⁡ ⁡ ()H()j⋅ ⋅ )){displaystyle tau _{g}=-{frac {domega }arg(H(jomega)}

La ganancia y el retardo de grupo para un filtro Chebyshev tipo I de quinto orden con ε=0,5 se trazan en el gráfico de la izquierda. Se puede ver que hay ondulaciones en la ganancia y el retardo de grupo en la banda de paso pero no en la banda de parada.

Configuración de la atenuación de corte

Atenuación de corte de banda de paso para filtros de Chebyshev es generalmente el mismo que la atenuación de la banda de paso, configurada por el ε ε {displaystyle varepsilon } computación arriba. Sin embargo, muchas aplicaciones como plegables y triplexers requieren una atenuación de corte de -3.0103 dB para obtener las reflexiones necesarias. Otras aplicaciones especializadas pueden requerir otros valores específicos para la atenuación de corte por diversas razones. Por lo tanto, es útil tener un medio disponible para establecer la atenuación de corte de banda de Chebyshev independientemente de la atenuación de la banda de paso, como -1 dB, -10 dB, etc. La atenuación de corte se establece por frecuencia escalando el denominador de la función de transferencia. Esto puede ser aproximado por las tablas de atenuación de corte de filtro interpolar Chebyshev, o calculado precisamente con el método de Newton.

El denominador puede ser escalado de frecuencia utilizando un factor de escalado al que nos referiremos como ⋅ ⋅ c{displaystyle omega _{c}. El denominador escalado de frecuencia de la función de transferencia Chebyshev puede ser reescrito para el n=3{displaystyle n=3} caso en términos de variable de escalado de frecuencia ⋅ ⋅ c{displaystyle omega _{c} como sigue:

H()s)=C()s/⋅ ⋅ c)3+A()s/⋅ ⋅ c)2+Bs/⋅ ⋅ c+C{displaystyle H(s)={(s/omega _{c})^{3}+A(s/omega _{c})^{2}+Bs/omega ¿Qué?

La tarea de modificar H()s){displaystyle H(s)} es encontrar un ⋅ ⋅ c{displaystyle omega _{c} que resulta en la atenuación deseada a 1 radio/s para la función de transferencia normalizada. El método de Newton se puede resumir fácilmente para hacer esto por su definición básica:

⋅ ⋅ a=⋅ ⋅ a+()SilencioH()j⋅ ⋅ a)Silencio− − Atenuación deseada)/()dSilencioH()j⋅ ⋅ a)Silencio/dj⋅ ⋅ a){displaystyle omega _{a}=omega _{a}+(foreverH(jomega _{a}) eterna-{text{DesiredAttenuation}})/(d imperH(jomega _{a})

mediante sucesivas iteraciones ⋅ ⋅ a{displaystyle omega _{a} hasta ⋅ ⋅ a{displaystyle omega _{a}es la frecuencia que atenua SilencioH()j⋅ ⋅ a)Silencio{displaystyle SilencioH(jomega _{a}a la atenuación deseada a 1 radio/s.

Si bien el resumen anterior puede ser conciso y fácil de entender, la mecánica de obtener un derivado preciso de la función de magnitud a lo largo de la j⋅ ⋅ {displaystyle jomega } El eje puede ser problemático. Se pueden utilizar técnicas digitales, pero generalmente es mejor aplicar el método de Newton con funciones continuas, si es posible, para maximizar la precisión. Por lo tanto, es útil modificar la expresión para eliminar el exceso de funciones matemáticas haciendo las siguientes alteraciones:

1) Multiply H()s){displaystyle H(s)} por H()− − s){displaystyle H(-s)} para obtener H()s)H()− − s){displaystyle H(s)H(-s)}. Esto eliminará los resultados numéricos complejos al evaluar SilencioH()s)H()− − s)Silencio{displaystyle TENH(s)H(-s) eliminando los términos de orden extraño en el polinomio.

2) En H()s)H()− − s){displaystyle H(s)H(-s)}, negate all terms of sn{displaystyle s^{n} cuando n+2{displaystyle n+2} es divisible por 4. Eso sería s2{displaystyle s^{2}, s6{displaystyle s^{6}, s10{displaystyle s^{10}, y así sucesivamente. Llamaremos a la función modificada H2()s)H2()− − s){displaystyle H_{2}(s)H_{2}(-s)}, y esta modificación permitirá el uso de números reales en lugar de números complejos al evaluar el polinomio y su derivado. Es decir, ahora podemos usar lo real ⋅ ⋅ a{displaystyle omega _{a}en lugar del complejo j⋅ ⋅ a{displaystyle jomega _{a}

3) Convertir la atenuación deseada en dB a un valor aritmético utilizando attenarith=10attendB/20{displaystyle atten_{arith}=10^{atten_{dB}/20}. Por ejemplo, -3.0103 dB es.7071, -1 dB es.8913 ans así sucesivamente. Esto simplifica la evaluación derivada.

4) Cuadrado la atenuación aritmética resultante para correlacionarse con el escuadrón de la H()s){displaystyle H(s)} función.

5) Calcular la modificación H2()⋅ ⋅ a)H2()− − ⋅ ⋅ a){displaystyle H_{2}(omega _{a})H_{2}(-omega _{a}} en el método de Newton usando el valor real, ⋅ ⋅ a{displaystyle omega _{a}. Siempre toma el valor absoluto.

6) Calcular el derivado modificado H2()⋅ ⋅ a)H2()− − ⋅ ⋅ a){displaystyle H_{2}(omega _{a})H_{2}(-omega _{a}} con respecto al valor real, ⋅ ⋅ a{displaystyle omega _{a}. Negate la computación derivada para contabilizar los efectos debido a las modificaciones realizadas para crear H2()⋅ ⋅ a)H2()− − ⋅ ⋅ a){displaystyle H_{2}(omega _{a})H_{2}(-omega _{a}}. NO tome el valor absoluto del derivado.

Did you mean:

When steps 1) through 4) are compete, Newton 's method expression my be written:

⋅ ⋅ a=⋅ ⋅ a+()[H2()⋅ ⋅ a)H2()− − ⋅ ⋅ a)]− − Atenuación deseada)/()d[H2()⋅ ⋅ a)H2()− − ⋅ ⋅ a)]/d⋅ ⋅ a){displaystyle omega _{a}=omega _{a}+([H_{2}(omega _{a})H_{2}(-omega _{a})-{text{DesiredAttenuation}})/(d[H_{2}(omegad)

usando un valor real para ⋅ ⋅ a{displaystyle omega _{a}sin necesidad aritmética compleja. El movimiento de ⋅ ⋅ a{displaystyle omega _{a} debe limitarse a evitar que vaya menos de 1 radio/s y a las frecuencias de onda tempranas en las iteraciones para aumentar la fiabilidad. Cuando esté completo, invertido ⋅ ⋅ a{displaystyle omega _{a}para obtener ⋅ ⋅ c{displaystyle omega _{c}que se puede utilizar para escalar el original H()s){displaystyle H(s)} función de transferencia denominador. La atenuación de H()s/⋅ ⋅ c){displaystyle H(s/omega _{c})} entonces será virtualmente el valor deseado exacto en 1 radio/s. Si se realiza correctamente, sólo se necesita un puñado de iteraciones para establecer la atenuación a través de una amplia gama de valores de atenuación deseados para filtros Chebyshev de orden pequeño y muy grande.

Filtros Chebyshev tipo II (filtros Chebyshev inversos)

También conocido como filtros Chebyshev inversos, el tipo de filtro Chebyshev tipo II es menos común porque no se activa tan rápido como el tipo I y requiere más componentes. No tiene ondulación en la banda de paso, pero tiene ondulación equivalente en la banda de parada. La ganancia es:

Gn()⋅ ⋅ )=11+1ε ε 2Tn2()⋅ ⋅ 0/⋅ ⋅ )=ε ε 2Tn2()⋅ ⋅ 0/⋅ ⋅ )1+ε ε 2Tn2()⋅ ⋅ 0/⋅ ⋅ ).{displaystyle G_{n}(omega)={frac {1}{sqrt {1+{frac {1}{varepsilon {fn} {fn} {fn}}}= {fnfnfnfn} {fnfn} {fnfn}fnfnK} {fnfnfnfnfnfnfnK} {fnfnfnfnfnfnfnfnfnK}}}}}}}}}}}fn}}}}}}}}}}}}}}}\\\fnfnfnfnfnfnfnfnfnfnfnfnfnfnfn}fn}}}fnfnfnfn\fnfn}}}}fn}\fn}fnfnfnfnfnfn}}}\fn} ^{2}T_{n} {2}(omega {0}/omega)}{1+varepsilon ¿Qué?

En la stopband, el polinomio de Chebyshev oscila entre -1 y 1 por lo que la ganancia oscilará entre cero y

11+1ε ε 2{displaystyle {frac {1}}}}}}

y la frecuencia más pequeña a la que se alcanza este máximo es la frecuencia de corte ⋅ ⋅ o{displaystyle omega _{o}. El parámetro ε está relacionado con la atenuación de la banda de parada γ en decibeles por:

ε ε =110γ γ /10− − 1.{displaystyle varepsilon ={frac {1}{sqrt {10^{gamma} /10}}}}

Para una atenuación de banda suprimida de 5 dB, ε = 0,6801; para una atenuación de 10 dB, ε = 0,3333. La frecuencia f₀ = ω₀/2π es la frecuencia de corte. La frecuencia de 3 dB f_H está relacionada con f₀ por:

fH=f0cosh⁡ ⁡ ()1ncosh− − 1⁡ ⁡ 1ε ε ).{displaystyle F_{H}={frac {f} {f}{f} {f} {f} {f}} {ccH00f} {f}} {cf}} {cccH0}}} {ccccccH00cH0} {ccH0}}} {ccccccccH0}}}}ccccH00ccccccccH00cccH00cccccccccccccccccccccccccccccccccccccccccccccccccccccc {1} {varepsilon}derecho)}}

Showing translation for

Poles and zeros

Suponiendo que la frecuencia de corte sea igual a la unidad, los polos ()⋅ ⋅ pm){displaystyle (omega _{pm})} de la ganancia del filtro Chebyshev son los ceros del denominador de la ganancia:

1+ε ε 2Tn2()− − 1/jspm)=0.{displaystyle 1+varepsilon ^{2}T_{n} {2}(-1/js_{pm}=0.}

Los polos de ganancia del filtro Chebyshev tipo II son los inversos de los polos del filtro tipo I:

1spm± ± =± ± pecado⁡ ⁡ ()1narsinh()1ε ε ))pecado⁡ ⁡ ()Silencio Silencio m){displaystyle {frac {1}{pm}{pm }}=pm sinh left({frac {1}{n}mathrm {arsinh} left({frac {1}{varepsilon }right)derecha)sin(theta _{m}}}}

+jcosh⁡ ⁡ ()1narsinh()1ε ε ))#⁡ ⁡ ()Silencio Silencio m){displaystyle qquad +jcosh left({frac {1}{n}mathrm {arsinh} left({frac {1}{varepsilon }}right)cos(theta _{m}}}}}}}}}}}

Donde m=1,2,...n{displaystyle m=1,2,...n}. Los ceros ()⋅ ⋅ zm){displaystyle (omega _{zm})} del filtro Chebyshev tipo II son los ceros del numerador de la ganancia:

ε ε 2Tn2()− − 1/jszm)=0.{displaystyle varepsilon ^{2}T_{n} {2}(-1/js_{zm}=0.,}

Los ceros del filtro de Chebyshev tipo II son, por lo tanto, el inverso de los ceros del polinomio de Chebyshev.

1/szm=− − j#⁡ ⁡ ()π π 22m− − 1n){displaystyle 1/s_{zm}=-jcos left({frac {pi }{2},{frac {2m-1}{n}right)}

para m=1,2,...n{displaystyle m=1,2,...n}.

La función de transferencia

Did you mean:

The transfer function is given by the poles in the left half plane of the gain function, and has the same zeros but these zeroes are single rather than double zeroes.

El retraso del grupo

La ganancia y el retardo de grupo para un filtro Chebyshev tipo II de quinto orden con ε=0,1 se trazan en el gráfico de la izquierda. Se puede ver que hay ondulaciones en la ganancia en la banda de parada pero no en la banda de paso.

Implementación

Topología de Cauer

Se puede realizar un filtro pasivo LC Chebyshev de baja velocidad utilizando una topología Cauer. Los valores de inductor o condensador de un n{displaystyle n}se puede calcular el filtro de prototipo Chebyshev a partir de las siguientes ecuaciones:

G0=1{displaystyle G_{0}=1}

G1=2A1γ γ {displaystyle G_{1}={frac {2A_{1}{gamma }

Gk=4Ak− − 1AkBk− − 1Gk− − 1,k=2,3,4,...... ,n{displaystyle G_{k}={frac {4A_{k-1} {B_{k-1}G_{k-1}}}}qquad k=2,3,4,dotsn}

Gn+1={}1sinextrañoCoth2⁡ ⁡ ()β β 4)sinincluso{displaystyle G_{n+1}={begin{cases}1 limit{text{if }n{text{ odd}\coth ^{2}left({frac {beta {fnMicrosoft Sans Serif}

G₁, G_k son los valores del elemento capacitor o ductor. f_H, la frecuencia 3 dB se calcula con: fH=f0cosh⁡ ⁡ ()1ncosh− − 1⁡ ⁡ 1ε ε ){displaystyle F_{H}=f_{0}cosh left({frac {1} {}}}derecha)}

Los coeficientes A, γ, β, A_k y B_k pueden calcularse a partir de las siguientes ecuaciones:

γ γ =pecado⁡ ⁡ ()β β 2n){displaystyle gamma =sinh left({frac {beta }{2n}right)}

β β =In⁡ ⁡ [Coth⁡ ⁡ ()δ δ 17.37)]{displaystyle beta =ln left[coth left({frac {delta }{17.37}right)right]}

Ak=pecado⁡ ⁡ ()2k− − 1)π π 2n,k=1,2,3,...... ,n{displaystyle A_{k}=sin {frac {(2k-1)pi }{2n},qquad k=1,2,3,dotsn}

Bk=γ γ 2+pecado2⁡ ⁡ ()kπ π n),k=1,2,3,...... ,n{displaystyle B_{k}=gamma ^{2}+sin ^{2}left({frac {kpi}{n}}right),qquad k=1,2,3,dotsn}

Donde δ δ {displaystyle delta } es el vendaje de los decibeles. El número 17.37{displaystyle 17.37} se redondea del valor exacto 40/In⁡ ⁡ ()10){displaystyle 40/ln(10)}.

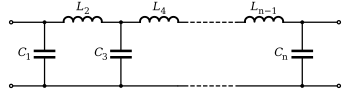
Los valores G_k calculados se pueden convertir en capacitores en derivación e inductores en serie como se muestra a la derecha, o se pueden convertir en condensadores en serie e inductores en derivación. Por ejemplo,

• C_{1 shunt} G₁, L_{2 series} = G₂,...

o

• L_{1 shunt} = G₁, C_{1 serie} = G₂,...

Tenga en cuenta que cuando G₁ es un capacitor en derivación o un inductor en serie, G₀ corresponde a la resistencia o conductancia de entrada, respectivamente. La misma relación es válida para G_n+1 y G_n. El circuito resultante es un filtro de paso bajo normalizado. Usando transformaciones de frecuencia y escalado de impedancia, el filtro de paso bajo normalizado puede transformarse en filtros de paso alto, paso de banda y supresión de banda de cualquier frecuencia de corte o ancho de banda deseado.

Digital

Al igual que con la mayoría de los filtros analógicos, el Chebyshev se puede convertir a una forma recursiva digital (de tiempo discreto) a través de la transformada bilineal. Sin embargo, como los filtros digitales tienen un ancho de banda finito, la forma de respuesta del Chebyshev transformado está distorsionada. Alternativamente, se puede usar el método de transformada Z emparejada, que no distorsiona la respuesta.

Comparación con otros filtros lineales

La siguiente ilustración muestra los filtros Chebyshev junto a otros tipos de filtros comunes obtenidos con el mismo número de coeficientes (quinto orden):

Los filtros Chebyshev son más nítidos que el filtro Butterworth; no son tan nítidos como el elíptico, pero muestran menos ondas en el ancho de banda.