Filtro adaptativo

Un filtro adaptativo es un sistema con un filtro lineal que tiene una función de transferencia controlada por parámetros variables y un medio para ajustar esos parámetros de acuerdo con un algoritmo de optimización. Debido a la complejidad de los algoritmos de optimización, casi todos los filtros adaptativos son filtros digitales. Se requieren filtros adaptativos para algunas aplicaciones porque algunos parámetros de la operación de procesamiento deseada (por ejemplo, las ubicaciones de las superficies reflectantes en un espacio reverberante) no se conocen de antemano o están cambiando. El filtro adaptativo de bucle cerrado utiliza la retroalimentación en forma de una señal de error para refinar su función de transferencia.

En términos generales, el proceso adaptativo de bucle cerrado implica el uso de una función de costo, que es un criterio para el rendimiento óptimo del filtro, para alimentar un algoritmo, que determina cómo modificar la función de transferencia del filtro para minimizar el costo en el siguiente iteración. La función de costo más común es el cuadrado medio de la señal de error.

A medida que ha aumentado la potencia de los procesadores de señales digitales, los filtros adaptativos se han vuelto mucho más comunes y ahora se usan de forma rutinaria en dispositivos como teléfonos móviles y otros dispositivos de comunicación, videocámaras y cámaras digitales, y equipos de monitoreo médico.

Aplicación de ejemplo

El registro de un latido cardíaco (un ECG) puede verse afectado por el ruido de la red eléctrica de CA. La frecuencia exacta de la potencia y sus armónicos pueden variar de un momento a otro.

Una forma de eliminar el ruido es filtrar la señal con un filtro de muesca en la frecuencia de la red y sus alrededores, pero esto podría degradar excesivamente la calidad del ECG, ya que es probable que el latido del corazón también tenga componentes de frecuencia en el rango rechazado..

Para eludir esta posible pérdida de información, se podría utilizar un filtro adaptable. El filtro adaptativo tomaría información tanto del paciente como de la red eléctrica y, por lo tanto, podría rastrear la frecuencia real del ruido a medida que fluctúa y restar el ruido de la grabación. Esta técnica adaptativa generalmente permite un filtro con un rango de rechazo más pequeño, lo que significa, en este caso, que la calidad de la señal de salida es más precisa para fines médicos.

Diagrama de bloques

La idea detrás de un filtro adaptativo de circuito cerrado es que un filtro variable se ajusta hasta que se minimiza el error (la diferencia entre la salida del filtro y la señal deseada). El filtro Least Mean Squares (LMS) y el filtro Recursive Least Squares (RLS) son tipos de filtros adaptativos.

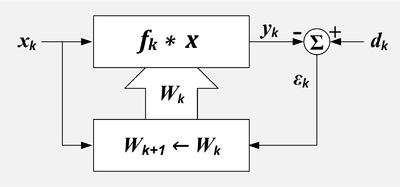Filtro adaptativo. k = número de muestra, x = entrada de referencia, X = conjunto de valores recientes de x, d = entrada deseada, W = conjunto de coeficientes de filtro, ε = salida de error, f = respuesta de impulso de filtro, * = convolution, Governing = summation, filtro lineal superior box=, algoritmo inferior de la caja=adapción

Filtro adaptativo, representación compacta. k = número de muestra, x = entrada de referencia, d = entrada deseada, ε = salida de error, f = respuesta del impulso del filtro, Governing = summation, box=filtro lineal y algoritmo de adaptación.

Hay dos señales de entrada al filtro adaptativo: dk{displaystyle D_{k} y xk{displaystyle x_{k} que a veces se llaman aportación primaria y el de referencia respectivamente. El algoritmo de adaptación intenta filtrar la entrada de referencia en una réplica de la entrada deseada minimizando la señal residual, ε ε k{displaystyle epsilon _{k}. Cuando la adaptación es exitosa, la salida del filtro Sí.k{displaystyle y_{k} es efectivamente una estimación de la señal deseada.

dk{displaystyle D_{k} que incluye la señal deseada más interferencia y

xk{displaystyle x_{k} que incluye las señales que están correlacionadas con algunas de las interferencias no deseadas dk{displaystyle D_{k}.

k representa el número de muestra discreta.

El filtro está controlado por un conjunto de coeficientes o pesos L+1.

Wk=[w0k,w1k,...,wLk]T{displaystyle mathbf {W} _{k}=left[w_{0k},,w_{1k},,...,,w_{Lk}right] representa el conjunto o vector de pesos, que controlan el filtro en el tiempo de la muestra k.

Donde wlk{displaystyle w_{lk} se refiere a l{displaystyle l}El peso a la hora k'th.

Δ Δ Wk{displaystyle mathbf {Delta W} _{k} representa el cambio en los pesos que ocurre como resultado de ajustes calculados en el tiempo de la muestra k.

Estos cambios se aplicarán después del tiempo de la muestra k y antes de que se utilicen en el tiempo de la muestra k+1.

La salida es generalmente ε ε k{displaystyle epsilon _{k} pero podría ser Sí.k{displaystyle y_{k} o incluso podría ser los coeficientes de filtro.(Widrow)

Las señales de entrada se definen de la siguiente manera:

dk=gk+uk+vk{displaystyle ¿Qué?

xk=gk.+uk.+vk.{displaystyle ¿Qué?

Donde:

g = la señal deseada,

g' = una señal que está correlacionada con la señal deseada g ,

u = una señal no deseada que se agrega g , pero no correlacionado con g o g'

u' = una señal que está correlacionada con la señal no deseada u, pero no correlacionado con g o g',

v = una señal no deseada (sonido típicamente aleatorio) no correlacionada con g, g', u, u' o v',

v' = una señal no deseada (sonido típicamente aleatorio) no correlacionada con g, g', u, u' o v.

Las señales de salida se definen de la siguiente manera:

Sí.k=g^ ^ k+u^ ^ k+v^ ^ k{displaystyle Y... {g}_{k}+{hat {fnK} {fnK} {fnK}fnK} {fnK}}} {fnK}} {f}}fn}fnfnfnfn}fnfnfnf}}fnf}}\fnfnfnfnfnf}}}}}}}}}\\fn\fnfn\\\fnfnfnfn}}}}}}}}\\\\\\fnf}}}}}}}}}}}}\\\fn}}}}}}}}}}}}}\\\\\\\fn}}}}}}}}}}}}}}}}}}}}}}\\\\\\\\\ {fnK}

ε ε k=dk− − Sí.k{displaystyle epsilon - Sí..

Donde:

g^ ^ {displaystyle {hat {g}} = la salida del filtro si la entrada era solamente g',

u^ ^ {displaystyle {hat {u}}} = la salida del filtro si la entrada era solamente u',

v^ ^ {displaystyle {hat {}}} = la salida del filtro si la entrada era solamente v'.

Filtro FIR de línea de retardo pulsado

Si el filtro variable tiene una estructura de respuesta de impulso finito (FIR) de línea de retardo, entonces la respuesta de impulso es igual a los coeficientes del filtro. La salida del filtro viene dada por

Sí.k=.. l=0Lwlkx()k− − l)=g^ ^ k+u^ ^ k+v^ ^ k{displaystyle Y... ¿Por qué? {fnK} {fnK} {fnK}fnK} {fnK}}} {fnK}} {f}}fn}fnfnfnfn}fnfnfnf}}fnf}}\fnfnfnfnfnf}}}}}}}}}\\fn\fnfn\\\fnfnfnfn}}}}}}}}\\\\\\fnf}}}}}}}}}}}}\\\fn}}}}}}}}}}}}}\\\\\\\fn}}}}}}}}}}}}}}}}}}}}}}\\\\\\\\\ {fnK}

Donde wlk{displaystyle w_{lk} se refiere a l{displaystyle l}El peso a la hora k'th.

Caso ideal

En el caso ideal v↑ ↑ 0,v.↑ ↑ 0,g.↑ ↑ 0{displaystyle vequiv 0,v'equiv 0,g'equiv 0}. Todas las señales no deseadas en dk{displaystyle D_{k} están representados por uk{displaystyle U_{k}. xk{displaystyle x_{k} consiste enteramente de una señal correlacionada con la señal no deseada en uk{displaystyle U_{k}.

La salida del filtro variable en el caso ideal es

Sí.k=u^ ^ k{displaystyle Y... {fnK}.

La señal de error o función de coste es la diferencia entre dk{displaystyle D_{k} y Sí.k{displaystyle y_{k}

ε ε k=dk− − Sí.k=gk+uk− − u^ ^ k{displaystyle epsilon ¿Qué? {fnK}. La señal deseada g_k pasa sin ser cambiado.

La señal de error ε ε k{displaystyle epsilon _{k} se minimiza en el sentido cuadrado medio cuando [uk− − u^ ^ k]{displaystyle [u_{k}-{hat {u}_{k}} se minimiza. En otras palabras, u^ ^ k{fnMicrosoft Sans Serif} es la mejor estimación media cuadrada de uk{displaystyle U_{k}. En el caso ideal, uk=u^ ^ k{displaystyle U_{k}={hat {fnK} y ε ε k=gk{displaystyle epsilon ¿Qué?, y todo lo que queda después de la resta es g{displaystyle g} que es la señal deseada sin cambios con todas las señales no deseadas eliminadas.

Componentes de señal en la entrada de referencia

En algunas situaciones, la entrada de referencia xk{displaystyle x_{k} incluye componentes de la señal deseada. Esto significa g' √≥ 0.

La cancelación perfecta de la interferencia no deseada no es posible en este caso, pero es posible mejorar la relación señal/interferencia. La salida será

ε ε k=dk− − Sí.k=gk− − g^ ^ k+uk− − u^ ^ k{displaystyle epsilon - Sí. {fnK} {fnK} {fnK} {fnK}. La señal deseada será modificada (generalmente bajada).

La relación entre la señal de salida y la interferencia tiene una fórmula simple denominada inversión de potencia.

*** *** out()z)=1*** *** ref()z){displaystyle rho _{mathsf {out}(z)={frac {1}{rho _{mathsf {ref}(z)}}}.

Donde

*** *** out()z){displaystyle rho _{mathsf {out}(z) } = señal de salida a relación de interferencia.

*** *** ref()z){displaystyle rho _{mathsf {ref}(z) } = señal de referencia a la relación de interferencia.

z{displaystyle z} = frecuencia en el dominio z.

Esta fórmula significa que la relación entre la señal de salida y la interferencia en una frecuencia particular es el recíproco de la relación entre la señal y la interferencia de referencia.

Ejemplo: un restaurante de comida rápida tiene una ventanilla de autoservicio. Antes de llegar a la ventana, los clientes hacen su pedido hablando por un micrófono. El micrófono también capta el ruido del motor y del entorno. Este micrófono proporciona la señal principal. La potencia de la señal de la voz del cliente y la potencia del ruido del motor son iguales. Es difícil para los empleados del restaurante entender al cliente. Para reducir la cantidad de interferencia en el micrófono principal, se ubica un segundo micrófono donde se pretende captar los sonidos del motor. También recoge la voz del cliente. Este micrófono es la fuente de la señal de referencia. En este caso, el ruido del motor es 50 veces más potente que la voz del cliente. Una vez que el cancelador haya convergido, la relación señal principal a interferencia mejorará de 1:1 a 50:1.

Combinador Lineal Adaptativo

Combinador lineal adaptativo que muestra el combinador y el proceso de adaptación. k = número de muestra, índice variable n=input, x = entradas de referencia, d = entrada deseada, W = conjunto de coeficientes de filtro, ε = salida de error, Governing = summation, superior box=linear combiner, inferior box=adaption algoritmo.

Combinador lineal adaptativo, representación compacta. k = número de muestra, índice variable n=input, x = entradas de referencia, d = entrada deseada, ε = salida de error, Governing = summation.

El combinador lineal adaptativo (ALC) se asemeja al filtro FIR de línea de retardo con tomas adaptativas, excepto que no hay una relación supuesta entre los valores X. Si los valores X fueran de las salidas de una línea de retardo intervenida, entonces la combinación de línea de retardo intervenida y ALC comprendería un filtro adaptativo. Sin embargo, los valores X podrían ser los valores de una matriz de píxeles. O podrían ser las salidas de múltiples líneas de retardo intervenidas. El ALC encuentra uso como formador de haz adaptativo para conjuntos de hidrófonos o antenas.

Sí.k=.. l=0Lwlkxlk=WkTxk{displaystyle Y... ¿Qué? ¿Qué?

Donde wlk{displaystyle w_{lk} se refiere a l{displaystyle l}El peso a la hora k'th.

Algoritmo LMS

Si el filtro variable tiene una estructura FIR de línea de retardo con derivación, entonces el algoritmo de actualización de LMS es especialmente simple. Normalmente, después de cada muestra, los coeficientes del filtro FIR se ajustan de la siguiente manera:(Widrow)

para l=0...... L{displaystyle l=0dots L}

wl,k+1=wlk+2μ μ ε ε kxk− − l{displaystyle w_{l,k+1}=w_{lk}+2mu \epsilon _{k} x_{k-l}

μ se llama factor de convergencia.

El algoritmo LMS no requiere que los valores X tengan una relación particular; por lo tanto, se puede utilizar para adaptar un combinador lineal y un filtro FIR. En este caso, la fórmula de actualización se escribe como:

wl,k+1=wlk+2μ μ ε ε kxlk{displaystyle w_{l,k+1}=w_{lk}+2mu \epsilon _{k} x_{lk}}

El efecto del algoritmo LMS es cada vez, k, para hacer un pequeño cambio en cada peso. La dirección del cambio es tal que disminuiría el error si se hubiera aplicado a tiempo k. La magnitud del cambio en cada peso depende de μ, el valor X asociado y el error a la vez k. Los pesos que hacen la mayor contribución a la salida, Sí.k{displaystyle y_{k}, se cambian más. Si el error es cero, entonces no debe haber cambio en los pesos. Si el valor asociado de X es cero, entonces cambiar el peso no marca ninguna diferencia, por lo que no se cambia.

Convergencia

μ controla qué tan rápido y qué tan bien el algoritmo converge a los coeficientes de filtro óptimos. Si μ es demasiado grande, el algoritmo no convergerá. Si μ es demasiado pequeño, el algoritmo converge lentamente y es posible que no pueda rastrear las condiciones cambiantes. Si μ es grande pero no demasiado grande para evitar la convergencia, el algoritmo alcanza el estado estacionario rápidamente pero sobrepasa continuamente el vector de peso óptimo. A veces, μ se hace grande al principio para una convergencia rápida y luego se reduce para minimizar el sobreimpulso.

Widrow y Stearns afirman en 1985 que no tienen conocimiento de una prueba de que el algoritmo LMS convergerá en todos los casos.

Sin embargo, bajo ciertas suposiciones sobre la estacionariedad y la independencia, se puede demostrar que el algoritmo convergerá si

<math alttext="{displaystyle 0<mu 0.μ μ .1σ σ 2{displaystyle 0 wonmu } {sigma }} {}}} {fn}} {fn} {fn}}<img alt="0<mu

Donde

σ σ 2=.. l=0Lσ σ l2{displaystyle sigma ^{2}=sum ¿Qué? = suma de todo el poder de entrada

σ σ l{displaystyle sigma _{l} es el valor RMS del l{displaystyle l}'th input

En el caso del filtro de línea de retardo con derivación, cada entrada tiene el mismo valor RMS porque son simplemente los mismos valores retardados. En este caso la potencia total es

σ σ 2=()L+1)σ σ 02{displaystyle sigma ^{2}=(L+1)sigma ¿Qué?

Donde

σ σ 0{displaystyle sigma ¿Qué? es el valor de RMS xk{displaystyle x_{k}, el flujo de entrada.

Esto conduce a un algoritmo LMS normalizado:

wl,k+1=wlk+()2μ μ σ σ σ σ 2)ε ε kxk− − l{displaystyle w_{l,k+1}=w_{lk}+left({frac {2mu _{sigma ¿Qué? x_{k-l} en cuyo caso los criterios de convergencia se convierten: <math alttext="{displaystyle 0<mu _{sigma }0.μ μ σ σ .1{displaystyle 0 mademu _{sigma ♪♪<img alt="0<mu _{{sigma }}.

Filtros adaptativos no lineales

El objetivo de los filtros no lineales es superar las limitaciones de los modelos lineales. Existen algunos enfoques de uso común: Volterra LMS, filtro adaptativo Kernel, filtro adaptativo Spline y filtro adaptativo Urysohn. Muchos autores incluyen también redes neuronales en esta lista. La idea general detrás de Volterra LMS y Kernel LMS es reemplazar las muestras de datos por diferentes expresiones algebraicas no lineales. Para Volterra LMS esta expresión es serie Volterra. En Spline Adaptive Filter, el modelo es una cascada de bloques dinámicos lineales y no linealidad estática, que se aproxima mediante splines. En Urysohn Adaptive Filter los términos lineales en un modelo

Sí.i=.. j=0mwjxij{displaystyle Y... ¿Qué? x_{ij}}

son reemplazadas por funciones lineales por partes

Sí.i=.. j=0mfj()xij){displaystyle Y...

que se identifican a partir de muestras de datos.

Aplicaciones de filtros adaptativos

• Cancelación de ruido adaptativo
• Control de ruido acústico
• Predicción de señales
• Cancelación de la retroalimentación
• Cancelación de Eco

Implementaciones de filtros

• Filtro de mínimos cuadrados medios
• Filtro Recursive menos cuadrados
• Filtro adaptador de frecuencia de bloque multidelay