Ferroelectricidad
La ferroelectricidad es una característica de ciertos materiales que tienen una polarización eléctrica espontánea que puede revertirse mediante la aplicación de un campo eléctrico externo. Todos los ferroeléctricos son también piezoeléctricos y piroeléctricos, con la propiedad adicional de que su polarización eléctrica natural es reversible. El término se usa en analogía con el ferromagnetismo, en el que un material exhibe un momento magnético permanente. El ferromagnetismo ya se conocía cuando Joseph Valasek descubrió la ferroelectricidad en 1920 en la sal de Rochelle. Por lo tanto, el prefijo ferro, que significa hierro, se usó para describir la propiedad a pesar de que la mayoría de los materiales ferroeléctricos no contienen hierro. Los materiales que son ferroeléctricos y ferromagnéticos se conocen como multiferroicos.
Polarización
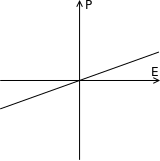
Cuando la mayoría de los materiales están eléctricamente polarizados, la polarización inducida, P, es casi exactamente proporcional al campo eléctrico externo aplicado E; por lo que la polarización es una función lineal. Esto se llama polarización dieléctrica lineal (ver figura). Algunos materiales, conocidos como materiales paraeléctricos, muestran una polarización no lineal más mejorada (ver figura). La permitividad eléctrica, correspondiente a la pendiente de la curva de polarización, no es constante como en los dieléctricos lineales sino que es función del campo eléctrico externo.
Además de ser no lineales, los materiales ferroeléctricos muestran una polarización espontánea distinta de cero (después del arrastre, vea la figura) incluso cuando el campo aplicado E es cero. La característica distintiva de los ferroeléctricos es que la polarización espontánea se puede revertir mediante un campo eléctrico adecuadamente fuerte aplicado en la dirección opuesta; por lo tanto, la polarización depende no solo del campo eléctrico actual sino también de su historial, lo que produce un ciclo de histéresis. Se denominan ferroeléctricos por analogía con los materiales ferromagnéticos, que tienen magnetización espontánea y exhiben bucles de histéresis similares.
Normalmente, los materiales muestran ferroelectricidad solo por debajo de cierta temperatura de transición de fase, llamada temperatura de Curie (TC) y son paraeléctricos por encima de esta temperatura: la polarización espontánea se desvanece, y el cristal ferroeléctrico se transforma en el estado paraeléctrico. Muchos ferroeléctricos pierden completamente sus propiedades piroeléctricas por encima de TC, porque su fase paraeléctrica tiene una estructura cristalina centrosimétrica.
Aplicaciones
La naturaleza no lineal de los materiales ferroeléctricos se puede utilizar para fabricar capacitores con capacitancia ajustable. Por lo general, un capacitor ferroeléctrico consiste simplemente en un par de electrodos intercalados en una capa de material ferroeléctrico. La permitividad de los ferroeléctricos no solo es ajustable, sino que comúnmente también es muy alta, especialmente cuando está cerca de la temperatura de transición de fase. Debido a esto, los capacitores ferroeléctricos tienen un tamaño físico pequeño en comparación con los capacitores dieléctricos (no sintonizables) de capacitancia similar.
La polarización espontánea de los materiales ferroeléctricos implica un efecto de histéresis que se puede utilizar como una función de memoria, y los condensadores ferroeléctricos se utilizan para fabricar RAM ferroeléctrica para ordenadores y tarjetas RFID. En estas aplicaciones, normalmente se utilizan películas delgadas de materiales ferroeléctricos, ya que esto permite que el campo requerido para cambiar la polarización se logre con un voltaje moderado. Sin embargo, cuando se utilizan películas delgadas, se debe prestar mucha atención a las interfaces, los electrodos y la calidad de la muestra para que los dispositivos funcionen de manera confiable.
Se requiere que los materiales ferroeléctricos por consideraciones de simetría sean también piezoeléctricos y piroeléctricos. Las propiedades combinadas de memoria, piezoelectricidad y piroelectricidad hacen que los condensadores ferroeléctricos sean muy útiles, p. para aplicaciones de sensores. Los condensadores ferroeléctricos se utilizan en máquinas de ultrasonido médicas (los condensadores generan y luego escuchan el pulso de ultrasonido utilizado para obtener imágenes de los órganos internos de un cuerpo), cámaras infrarrojas de alta calidad (la imagen infrarroja se proyecta en una matriz bidimensional de condensadores ferroeléctricos capaces de detectando diferencias de temperatura tan pequeñas como millonésimas de grado Celsius), sensores de incendio, sonar, sensores de vibración e incluso inyectores de combustible en motores diesel.
Otra idea de reciente interés es la unión de túnel ferroeléctrico (FTJ) en la que un contacto está formado por una película ferroeléctrica de un nanómetro de espesor colocada entre electrodos metálicos. El grosor de la capa ferroeléctrica es lo suficientemente pequeño como para permitir la formación de túneles de electrones. Los efectos piezoeléctricos y de interfaz, así como el campo de despolarización, pueden conducir a un efecto de conmutación de electrorresistencia gigante (GER).
Otra aplicación floreciente es la multiferroica, en la que los investigadores buscan formas de acoplar el ordenamiento magnético y ferroeléctrico dentro de un material o heteroestructura; Hay varias revisiones recientes sobre este tema.
Las propiedades catalíticas de los ferroeléctricos se han estudiado desde 1952, cuando Parravano observó anomalías en las tasas de oxidación de CO sobre los niobatos ferroeléctricos de sodio y potasio cerca de la temperatura de Curie de estos materiales. El componente perpendicular a la superficie de la polarización ferroeléctrica puede dopar las cargas dependientes de la polarización en las superficies de los materiales ferroeléctricos, cambiando su química. Esto abre la posibilidad de realizar catálisis más allá de los límites del principio de Sabatier. El principio de Sabatier establece que la interacción superficie-adsorbatos tiene que ser una cantidad óptima: no demasiado débil para ser inerte frente a los reactivos y no demasiado fuerte para envenenar la superficie y evitar la desorción de los productos: una situación de compromiso. Este conjunto de interacciones óptimas suele denominarse "cima del volcán" en parcelas de volcanes de actividad. Por otro lado, la química dependiente de la polarización ferroeléctrica puede ofrecer la posibilidad de cambiar la interacción superficie-adsorbatos de fuerte adsorción a fuerte desorción, por lo que ya no es necesario un compromiso entre desorción y adsorción. La polarización ferroeléctrica también puede actuar como un recolector de energía. La polarización puede ayudar a la separación de pares de agujeros de electrones generados por foto, lo que lleva a una fotocatálisis mejorada. Además, debido a los efectos piroeléctricos y piezoeléctricos bajo condiciones variables de temperatura (ciclos de calentamiento/enfriamiento) o tensión variable (vibraciones), pueden aparecer cargas adicionales en la superficie y provocar diversas reacciones (electro)químicas.
Materiales
Los dipolos eléctricos internos de un material ferroeléctrico están acoplados a la red del material, por lo que cualquier cambio en la red cambiará la fuerza de los dipolos (en otras palabras, un cambio en la polarización espontánea). El cambio en la polarización espontánea da como resultado un cambio en la carga superficial. Esto puede causar un flujo de corriente en el caso de un capacitor ferroeléctrico incluso sin la presencia de un voltaje externo a través del capacitor. Dos estímulos que cambiarán las dimensiones de la red de un material son la fuerza y la temperatura. La generación de una carga superficial en respuesta a la aplicación de una tensión externa a un material se denomina piezoelectricidad. Un cambio en la polarización espontánea de un material en respuesta a un cambio de temperatura se denomina piroelectricidad.
En general, hay 230 grupos espaciales entre los que se pueden encontrar 32 clases cristalinas en los cristales. Hay 21 clases no centrosimétricas, dentro de las cuales 20 son piezoeléctricas. Entre las clases de piezoeléctricos, 10 tienen una polarización eléctrica espontánea, que varía con la temperatura, por lo que son piroeléctricos. La ferroelectricidad es un subconjunto de la piroelectricidad, que aporta polarización electrónica espontánea al material.
| 32 Clases de cristalina | ||||
|---|---|---|---|---|
| 21 noncentrosymmetric | 11 centros simétricos | |||
| 20 clases piezoeléctrica | no piezoeléctrico | |||
| 10 clases piroeléctrica | no piroeléctrico | |||
| ferroelectric | no ferroelectric | |||
| por ejemplo: PbZr/TiO3, BaTiO3, PbTiO3, AlN | por ejemplo: Tourmaline, ZnO, | por ejemplo: Quartz, Langasite | ||
Las transiciones de fase ferroeléctricas a menudo se caracterizan como de desplazamiento (como BaTiO3) o desorden de orden (como NaNO2), aunque a menudo las transiciones de fase demostrarán elementos de ambos comportamientos. En el titanato de bario, un ferroeléctrico típico del tipo desplazable, la transición puede entenderse en términos de una catástrofe de polarización, en la que, si un ion se desplaza ligeramente del equilibrio, la fuerza de los campos eléctricos locales debido a los iones en el cristal aumenta más rápidamente que las fuerzas elásticas restauradoras. Esto conduce a un cambio asimétrico en las posiciones de los iones de equilibrio y, por lo tanto, a un momento dipolar permanente. El desplazamiento iónico en el titanato de bario se refiere a la posición relativa del ion titanio dentro de la jaula octaédrica de oxígeno. En el titanato de plomo, otro material ferroeléctrico clave, aunque la estructura es bastante similar a la del titanato de bario, la fuerza impulsora de la ferroelectricidad es más compleja y las interacciones entre los iones de plomo y oxígeno también juegan un papel importante. En un ferroeléctrico de orden-desorden, hay un momento dipolar en cada celda unitaria, pero a altas temperaturas apuntan en direcciones aleatorias. Al bajar la temperatura y pasar por la transición de fase, los dipolos se ordenan, todos apuntando en la misma dirección dentro de un dominio.
Un material ferroeléctrico importante para aplicaciones es el titanato de zirconato de plomo (PZT), que forma parte de la solución sólida formada entre el titanato de plomo ferroeléctrico y el zirconato de plomo antiferroeléctrico. Se utilizan diferentes composiciones para diferentes aplicaciones; para aplicaciones de memoria, se prefiere PZT en una composición más cercana al titanato de plomo, mientras que las aplicaciones piezoeléctricas hacen uso de los coeficientes piezoeléctricos divergentes asociados con el límite de fase morfotrópica que se encuentra cerca de la composición 50/50.
Los cristales ferroeléctricos a menudo muestran varias temperaturas de transición e histéresis de estructura de dominio, al igual que los cristales ferromagnéticos. La naturaleza de la transición de fase en algunos cristales ferroeléctricos aún no se comprende bien.
En 1974, R.B. Meyer usó argumentos de simetría para predecir cristales líquidos ferroeléctricos, y la predicción se pudo verificar de inmediato mediante varias observaciones del comportamiento relacionado con la ferroelectricidad en fases de cristal líquido esméctico que son quirales e inclinadas. La tecnología permite la construcción de monitores de pantalla plana. La producción en masa entre 1994 y 1999 estuvo a cargo de Canon. Los cristales líquidos ferroeléctricos se utilizan en la producción de LCoS reflectantes.
En 2010, David Field descubrió que las películas prosaicas de productos químicos como el óxido nitroso o el propano exhibían propiedades ferroeléctricas. Esta nueva clase de materiales ferroeléctricos exhibe "spontelectric" propiedades, y puede tener una amplia gama de aplicaciones en dispositivos y nanotecnología y también influir en la naturaleza eléctrica del polvo en el medio interestelar.
Otros materiales ferroeléctricos utilizados incluyen sulfato de triglicina, fluoruro de polivinilideno (PVDF) y tantalato de litio.
Debería ser posible producir materiales que combinen propiedades ferroeléctricas y metálicas simultáneamente, a temperatura ambiente. Según una investigación publicada en 2018 en Nature Communications, los científicos pudieron producir una imagen "bidimensional" hoja de material que era a la vez "ferroeléctrico" (tenía una estructura cristalina polar) y que conducía la electricidad.
Teoría
Puede encontrar una introducción a la teoría de Landau aquí. Según la teoría de Ginzburg-Landau, la energía libre de un material ferroeléctrico, en ausencia de un campo eléctrico y tensión aplicada, puede escribirse como una expansión de Taylor en términos del parámetro de orden, P. Si se utiliza una expansión de sexto orden (es decir, términos de octavo orden y superiores truncados), la energía libre viene dada por:
- Δ Δ E=12α α 0()T− − T0)()Px2+PSí.2+Pz2)+14α α 11()Px4+PSí.4+Pz4)+12α α 12()Px2PSí.2+PSí.2Pz2+Pz2Px2)+16α α 111()Px6+PSí.6+Pz6)+12α α 112[Px4()PSí.2+Pz2)+PSí.4()Px2+Pz2)+Pz4()Px2+PSí.2)]+12α α 123Px2PSí.2Pz2{displaystyle {begin{array}{ll} Delta E={frac {1}{2}alpha ¿Por qué? {1}{4}Alpha ¿Por qué? {1}{2}Alpha _{12}left(P_{x}{2}P_{y}}{2}+P_{y}} {2}P_{z}{2}+P_{z}{2}P_{x}}{2}right)}c}c}c}cH00}c}c}cc}c}c}c}c}c}c}cc}c}c}c}c}c}c}cc}c}c}ccccccc}c}c}c}cccc}cH00}cH00}c}cH00}cH00}ccc}c}cH00}cH00}ccH00}cH00}c}cH00}c}cH00} {1}{6}alpha _{111}left(P_{x}{6}+P_{y}^{6}+P_{z}{6}right)\\q]\q\q\q\\fnMicroc {2} {c}ccH00}cH00} {c}ccc}cccH00}ccH00}ccH00}cH00}cH00}cH00}cccH00}ccH00}cH00}cH00}cH00}cH00}}cH00} {cH00}}}ccc}ccc}c}c}c}}cccH00}}cH00}cccc}}ccc}c}cH00} {cH00}}}cc}cccccH00}c}cc}cH00}c}}c}}cH00}c}}cc}cc}}}}c}}} {1}{2}alpha ¿Qué?
Donde Px, PSí., y Pz son los componentes del vector de polarización en el x, Sí., y z direcciones, respectivamente, y los coeficientes, α α i,α α ij,α α ijk{displaystyle alpha _{i},alpha _{ij},alpha _{ijk}} debe ser consistente con la simetría de cristal. Para investigar la formación de dominios y otros fenómenos en ferroeléctricos, estas ecuaciones se utilizan a menudo en el contexto de un modelo de campo de fase. Típicamente, esto implica añadir un término gradiente, un término electrostático y un término elástico a la energía libre. Las ecuaciones se discretizan luego en una cuadrícula usando el método de diferencia finita o método de elemento finito y se resuelven sujeto a las restricciones de la ley de Gauss y elasticidad lineal.
En todos los ferroeléctricos conocidos, 0}" xmlns="http://www.w3.org/1998/Math/MathML">α α 0■0{displaystyle alpha ¿Qué?0" aria-hidden="true" class="mwe-math-fallback-image-inline" src="https://wikimedia.org/api/rest_v1/media/math/render/svg/b14ce96f05d42785bec56bd5b25960833f1b7818" style="vertical-align: -0.671ex; width:6.803ex; height:2.509ex;"/> y 0}" xmlns="http://www.w3.org/1998/Math/MathML">α α 111■0{displaystyle alpha _{111} {0}
0" aria-hidden="true" class="mwe-math-fallback-image-inline" src="https://wikimedia.org/api/rest_v1/media/math/render/svg/01369cf1c29694ebb9be7ebeb05e3e2665509ca7" style="vertical-align: -0.671ex; width:8.447ex; height:2.509ex;"/>. Estos coeficientes se pueden obtener experimentalmente o mediante simulaciones ab-initio. Para ferroeléctricos con una transición de primera orden, <math alttext="{displaystyle alpha _{11}α α 11.0{displaystyle alpha _{11}traducido0}<img alt="alpha _{{11}}, mientras 0}" xmlns="http://www.w3.org/1998/Math/MathML">α α 11■0{displaystyle alpha _{11}0}
0" aria-hidden="true" class="mwe-math-fallback-image-inline" src="https://wikimedia.org/api/rest_v1/media/math/render/svg/d8250f1bc5459df678532ac7d501d7d895ba8d34" style="vertical-align: -0.671ex; width:7.625ex; height:2.509ex;"/> para una segunda etapa de la transición.
La polarización espontánea, Ps de un ferroeléctrico para una transición de fase cúbica a tetragonal puede obtenerse considerando la expresión 1D de la energía libre que es:
- Δ Δ E=12α α 0()T− − T0)Px2+14α α 11Px4+16α α 111Px6{displaystyle Delta E={frac {1}{2}alpha ¿Por qué? ¿Por qué? {1}{6}alpha _{111}P_{x} {6}}} {c} {c} {c} {c} {c}}} {c}}} {c}}}} {c}}}}}c}c}}c}cc}cH9}c}c}cH9}}c}c}c}c}cH9}}cH9}c}c}c}c}c}c}c}c}cH9}cH9}c}c}c}c}c}c}c}c}cH9}cH9}cH9}c}c}c}c}cH9}c}c}cH9}cH9}c}c}c}c}c}cH00}c}c}c
Esta energía libre tiene la forma de un doble potencial de pozo con dos minima de energía libre en Px=Ps{displaystyle P_{x}=P_{s}, la polarización espontánea. Encontramos el derivado de la energía libre, y lo fijamos igual a cero para resolver por Ps{displaystyle P_{s}:
- ∂ ∂ Δ Δ E∂ ∂ Px=α α 0()T− − T0)Px+α α 11Px3+α α 111Px5{fnMicrosoft {fnMicrosoft {fnMicrosoft {fnMicrosoft {fnMicrosoft {\fnMicrosoft} Delta E}{partial P_{x}=alpha ¿Por qué? ¿Por qué?
- 0=∂ ∂ Δ Δ E∂ ∂ Px=Ps[α α 0()T− − T0)+α α 11Ps2+α α 111Ps4]{displaystyle 0={frac {partial Delta E}{partial P_{x}=P_{s}left[alpha] ¿Qué? (T-T_{0}right)+alpha ¿Por qué?
Dado que la solución Ps = 0 de esta ecuación corresponde más bien a un máximo de energía libre en la fase ferroeléctrica, las soluciones deseadas para Ps corresponden a poner el factor restante a cero:
- α α 0()T− − T0)+α α 11Ps2+α α 111Ps4=0{displaystyle alpha ¿Qué? (T-T_{0}right)+alpha - ¿Por qué? ¿Qué?
cuya solución es:
- Ps2=12α α 111[− − α α 11± ± α α 112+4α α 0α α 111()T0− − T)]{displaystyle ¿Por qué? _{11}{2}+4alpha _{0}alpha _{111}left(T_{0}-Tright)};right]
y eliminando las soluciones que toman la raíz cuadrada de un número negativo (ya sea para las transiciones de fase de primer o segundo orden) se obtiene:
- Ps=± ± 12α α 111[− − α α 11+α α 112+4α α 0α α 111()T0− − T)]{displaystyle P_{s}=pm {fnMicroc {1}{2alpha _{111}}left[-alpha _{11}+{sqrt {alpha}}lpha _{11}{2}+4alpha _{0}alpha _{111}left(T_{0}-Tright)}};right]}
Si α α 11=0{displaystyle alpha _{11}=0}, la solución para la polarización espontánea reduce a:
- Ps=± ± α α 0()T0− − T)α α 1114{displaystyle P_{s}=pm {sqrt[{4}}{frac {alpha _{0}left(T_{0}-Tright)}{alpha _{111}}}}}}} {fnK}}
El bucle de histéresis (Px frente a Ex) se puede obtener a partir de la expansión de energía libre incluyendo el término -Ex Px correspondiente a la energía debida a un campo eléctrico externo Ex interactuando con la polarización Px, como sigue:
- Δ Δ E=12α α 0()T− − T0)Px2+14α α 11Px4+16α α 111Px6− − ExPx{displaystyle Delta E={frac {1}{2}alpha ¿Por qué? ¿Por qué? {1}{6}alpha _{111}P_{x} {6}-E_{x}P_{x}
Encontramos los valores de polarización estables de Px bajo la influencia del campo externo, ahora denotados como Pe, nuevamente al establecer la derivada de la energía con respecto a Px a cero:
- ∂ ∂ Δ Δ E∂ ∂ Px=α α 0()T− − T0)Px+α α 11Px3+α α 111Px5− − Ex=0{fnMicrosoft {fnMicrosoft {fnMicrosoft {fnMicrosoft {fnMicrosoft {\fnMicrosoft} Delta E}{partial P_{x}=alpha ¿Por qué? ¿Por qué? ¿Qué?
- Ex=α α 0()T− − T0)Pe+α α 11Pe3+α α 111Pe5{displaystyle E_{x}=alpha ¿Por qué? ¿Por qué?
Plotting Ex (en el eje X) como una función Pe (pero en el eje Y) da una curva 'S' formada que es multivalorada en Pe para algunos valores de Ex. La parte central de la 'S' corresponde a un máximo local de energía libre (desde <math alttext="{displaystyle {frac {partial ^{2}Delta E}{partial P_{x}^{2}}}∂ ∂ 2Δ Δ E∂ ∂ Px2.0{displaystyle {frac {partial }Delta E}{partial ¡No!<img alt="{frac {partial ^{2}Delta E}{partial P_{x}^{2}}}). Eliminación de esta región, y conexión de las porciones superiores e inferiores de la curva 'S' por líneas verticales en la discontinuidad da el bucle de histeresis de polarización interna debido a un campo eléctrico externo.
Ferroelectricidad deslizante
La ferroelectricidad deslizante se encuentra ampliamente, pero solo en capas apiladas bidimensionales (2D) de van der Waals. La polarización eléctrica vertical se cambia mediante el deslizamiento de la capa intermedia en el plano.
Contenido relacionado
Corrimiento al rojo
Oscilador electronico
Magnetómetro


![{begin{array}{ll}Delta E=&{frac {1}{2}}alpha _{0}left(T-T_{0}right)left(P_{x}^{2}+P_{y}^{2}+P_{z}^{2}right)+{frac {1}{4}}alpha _{{11}}left(P_{x}^{4}+P_{y}^{4}+P_{z}^{4}right)\&+{frac {1}{2}}alpha _{{12}}left(P_{x}^{2}P_{y}^{2}+P_{y}^{2}P_{z}^{2}+P_{z}^{2}P_{x}^{2}right)\&+{frac {1}{6}}alpha _{{111}}left(P_{x}^{6}+P_{y}^{6}+P_{z}^{6}right)\&+{frac {1}{2}}alpha _{{112}}left[P_{x}^{4}left(P_{y}^{2}+P_{z}^{2}right)+P_{y}^{4}left(P_{x}^{2}+P_{z}^{2}right)+P_{z}^{4}left(P_{x}^{2}+P_{y}^{2}right)right]\&+{frac {1}{2}}alpha _{{123}}P_{x}^{2}P_{y}^{2}P_{z}^{2}end{array}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/86dd89a4c024727349d2f25a67004f08b54a21f9)





![{displaystyle 0={frac {partial Delta E}{partial P_{x}}}=P_{s}left[alpha _{0}left(T-T_{0}right)+alpha _{11}P_{s}^{2}+alpha _{111}P_{s}^{4}right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b21d633b20b5f0538ee05a8ed8dcc95a7f4be1c8)

![{displaystyle P_{s}^{2}={frac {1}{2alpha _{111}}}left[-alpha _{11}pm {sqrt {alpha _{11}^{2}+4alpha _{0}alpha _{111}left(T_{0}-Tright)}};right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b0649ed821a5a879411edbb3f258b5b4faf94093)
![{displaystyle P_{s}=pm {sqrt {{frac {1}{2alpha _{111}}}left[-alpha _{11}+{sqrt {alpha _{11}^{2}+4alpha _{0}alpha _{111}left(T_{0}-Tright)}};right]}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3ad2d062fca3d1a624fa3c66ec15ecd4950f449d)

![{displaystyle P_{s}=pm {sqrt[{4}]{frac {alpha _{0}left(T_{0}-Tright)}{alpha _{111}}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e128878a88a35c105d33ec3f36ce4a4e1314c0e4)


