Ferrimagnetismo

ImprimirCitar

Tipo de fenómeno magnético

Ordenación ferrimagnetica

Órdenes magnéticas: comparación entre ferro, antiferro y ferrimagnetismo

Un material ferrimagnético es un material que tiene poblaciones de átomos con momentos magnéticos opuestos, como en el antiferromagnetismo, pero estos momentos son desiguales en magnitud por lo que permanece una magnetización espontánea. Esto puede ocurrir, por ejemplo, cuando las poblaciones constan de diferentes átomos o iones (como Fe²⁺ y Fe³⁺).

El ferrimagnetismo a menudo se ha confundido con el ferromagnetismo. La sustancia magnética más antigua conocida, la magnetita (Fe₃O₄), se clasificó como ferromagnético antes de que Louis Néel descubriera el ferrimagnetismo en 1948. Desde el descubrimiento, se han encontrado numerosos usos para materiales ferrimagnéticos, como discos duros y aplicaciones biomédicas.

Historia

Hasta el siglo XX, todas las sustancias magnéticas naturales se denominaban ferromagnetos. En 1936, Louis Néel publicó un artículo en el que proponía la existencia de una nueva forma de magnetismo cooperativo que denominó antiferromagnetismo. Mientras trabajaba con Mn₂Sb, el físico francés Charles Guillaud descubrió que las teorías actuales sobre el magnetismo no eran adecuadas para explicar el comportamiento del material e hizo un modelo para explicar el comportamiento. En 1948, Néel publicó un artículo sobre un tercer tipo de magnetismo cooperativo, basado en los supuestos del modelo de Guillaud. Lo llamó ferrimagnetismo. En 1970, Néel fue galardonado por su trabajo en magnetismo con el Premio Nobel de Física.

Origen físico

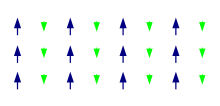
▪ Bajo el punto de compensación de magnetización, el material ferrimántico es magnético. En el punto de compensación, los componentes magnéticos se cancelan y el momento magnético total es cero.. Sobre la temperatura de Curie, el material pierde magnetismo.

El ferrimagnetismo tiene los mismos orígenes físicos que el ferromagnetismo y el antiferromagnetismo. En los materiales ferrimagnéticos, la magnetización también es causada por una combinación de interacciones dipolo-dipolo e interacciones de intercambio que resultan del principio de exclusión de Pauli. La principal diferencia es que en los materiales ferrimagnéticos hay diferentes tipos de átomos en la celda unitaria del material. Un ejemplo de esto se puede ver en la figura de la derecha. Aquí los átomos con un momento magnético más pequeño apuntan en dirección opuesta a los momentos más grandes. Esta disposición es similar a la presente en los materiales antiferromagnéticos, pero en los materiales ferrimagnéticos el momento neto es distinto de cero porque los momentos opuestos difieren en magnitud.

Los ferriimanes tienen una temperatura crítica por encima de la cual se vuelven paramagnéticos al igual que los ferroimanes. A esta temperatura (llamada temperatura de Curie) hay una transición de fase de segundo orden y el sistema ya no puede mantener una magnetización espontánea. Esto se debe a que a temperaturas más altas, el movimiento térmico es lo suficientemente fuerte como para exceder la tendencia de los dipolos a alinearse.

Derivación

Hay varias formas de describir los ferrimagnetos, la más simple de las cuales es con la teoría del campo medio. En la teoría del campo medio, el campo que actúa sobre los átomos se puede escribir como:

${displaystyle {overrightarrow {H}}={overrightarrow {H}}_{0}+{overrightarrow {H}}_{m}}$

Donde ${displaystyle {overrightarrow {H}}_{0}}$ es el campo magnético aplicado y ${displaystyle {overrightarrow {H}}_{m}}$ es el campo causado por las interacciones entre los átomos. En consecuencia, la siguiente hipótesis es: ${displaystyle {overrightarrow {H}}_{m}=gamma {overrightarrow {M}}}$

Aquí. ${textstyle {overrightarrow {M}}}$ es la magnetización promedio de la rejilla y $gamma$ es el coeficiente de campo molecular. Cuando permitimos ${textstyle {overrightarrow {M}}}$ y $gamma$ para ser dependientes de posición y orientación podemos escribirlo en el formulario:

${displaystyle {overrightarrow {H}}_{i}={overrightarrow {H}}_{0}+sum _{k=1}^{n}gamma _{ik}{overrightarrow {M}}_{k}}$

Aquí. ${displaystyle {overrightarrow {H}}_{i}}$ es el campo actuando en el i^T subestructura y ${displaystyle gamma _{ik}}$ es el coeficiente de campo molecular entre el i^T y el k^T subestructura. Para una celosía diatómica podemos designar dos tipos de sitios, A y B. Podemos designar $N$ el número de iones magnéticos por volumen de unidad, $lambda$ la fracción de los iones magnéticos en los sitios A, y ${textstyle mu =1-lambda }$ la fracción en los sitios B. Esto entonces da:

${displaystyle {overrightarrow {H}}_{aa}=gamma _{aa}{overrightarrow {M}};{overrightarrow {H}}_{ab}=gamma _{ab}{overrightarrow {M}}_{b};{overrightarrow {H}}_{ba}=gamma _{ba}{overrightarrow {M}}_{a};{overrightarrow {H}}_{bb}=gamma _{bb}{overrightarrow {M}}_{b}}$

Se puede demostrar que ${displaystyle gamma _{ab}=gamma _{ba}}$ y eso ${displaystyle gamma _{aa}neq gamma _{bb}}$ a menos que las estructuras sean idénticas. $0}" xmlns="http://www.w3.org/1998/Math/MathML">γ γ ab■0{displaystyle gamma _{ab}0}0}" aria-hidden="true" class="mwe-math-fallback-image-inline" src="https://wikimedia.org/api/rest_v1/media/math/render/svg/b38c1c83c6fedd81c374c0b73fa06d172230725b" style="vertical-align: -0.838ex; width:7.272ex; height:2.676ex;"/>$ favorece una alineación paralela de ${displaystyle {overrightarrow {M}}_{a}}$ y ${displaystyle {overrightarrow {M}}_{b}}$ , mientras $<math alttext="{displaystyle gamma _{ab}γ γ ab.0{displaystyle gamma _{ab}traducido0}<img alt="{displaystyle gamma _{ab}$ favorece una alineación antiparalela. Para ferrimagnets, $<math alttext="{displaystyle gamma _{ab}γ γ ab.0{displaystyle gamma _{ab}traducido0}<img alt="{displaystyle gamma _{ab}$ , así que será conveniente tomar $gamma_{ab}$ como una cantidad positiva y escribir el signo menos explícitamente delante de él. Para los campos totales en A y B esto da:

${displaystyle {overrightarrow {H}}_{a}={overrightarrow {H}}_{0}+gamma _{aa}{overrightarrow {M}}_{a}-gamma _{ab}{overrightarrow {M}}_{b}}$

${displaystyle {overrightarrow {H}}_{b}={overrightarrow {H}}_{0}+gamma _{bb}{overrightarrow {M}}_{b}-gamma _{ab}{overrightarrow {M}}_{a}}$

Además, introduciremos los parámetros ${displaystyle alpha ={frac {gamma _{aa}}{gamma _{ab}}}}$ y ${displaystyle beta ={frac {gamma _{bb}}{gamma _{ab}}}}$ que dan la relación entre las fortalezas de las interacciones. Por fin introduciremos las magnetizaciones reducidas:

${displaystyle {overrightarrow {sigma }}_{a}={overrightarrow {M}}_{a}/lambda Ngmu _{B}S_{a}}$

${displaystyle {overrightarrow {sigma }}_{b}={overrightarrow {M}}_{b}/mu Ngmu _{B}S_{b}}$

con $S_{i}$ la vuelta del yo^T elemento. Esto entonces da para los campos:

${displaystyle {overrightarrow {H}}_{a}={overrightarrow {H}}_{0}+Ngmu _{B}S_{a}gamma _{ab}(lambda alpha {overrightarrow {sigma }}_{a}-mu {overrightarrow {sigma }}_{b})}$

${displaystyle {overrightarrow {H}}_{b}={overrightarrow {H}}_{0}+Ngmu _{B}S_{b}gamma _{ab}(-lambda {overrightarrow {sigma }}_{a}+mu beta {overrightarrow {sigma }}_{b})}$

Las soluciones de estas ecuaciones (omitidas aquí) vienen dadas por

${displaystyle sigma _{a}=B_{S_{a}}(gmu _{b}S_{a}H_{a}/k_{B}T)}$

${displaystyle sigma _{b}=B_{S_{b}}(gmu _{b}S_{b}H_{b}/k_{B}T)}$

Donde ${displaystyle B_{J}(x)}$ es la función Brillouin. El caso más simple para resolver ahora es ${displaystyle S_{a}=S_{b}={frac {1}{2}}}$ . Desde ${displaystyle B_{frac {1}{2}}(x)=tanh(x)}$ . Esto entonces da el siguiente par de ecuaciones:

${displaystyle lambda sigma _{a}={frac {tau F(lambdaalphabeta)}{alpha beta -1}}(beta tanh ^{-1}sigma _{a}+tanh ^{-1}sigma _{b})}$

${displaystyle mu sigma _{b}={frac {tau F(lambdaalphabeta)}{alpha beta -1}}(tanh ^{-1}sigma _{a}+alpha tanh ^{-1}sigma _{b})}$

con ${displaystyle tau =T/T_{c}}$ y ${displaystyle F(lambdaalphabeta)={frac {1}{2}}(lambda alpha +mu beta +{sqrt {(lambda alpha -mu beta)^{2}+4lambda mu }})}$ . Estas ecuaciones no tienen una solución analítica conocida, por lo que deben resolverse numéricamente para encontrar la dependencia de temperatura de $mu$ .

Efectos de la temperatura

A diferencia del ferromagnetismo, las formas de las curvas de magnetización del ferrimagnetismo pueden tomar muchas formas diferentes dependiendo de la fuerza de las interacciones y la abundancia relativa de átomos. Los casos más notables de esta propiedad son que la dirección de la magnetización puede invertirse mientras se calienta un material ferrimagnético desde el cero absoluto hasta su temperatura crítica, y que la fuerza de la magnetización puede aumentar mientras se calienta un material ferrimagnético hasta la temperatura crítica, los cuales no pueden ocurrir. para materiales ferromagnéticos. Estas dependencias de la temperatura también se han observado experimentalmente en NiFe_2/5Cr_8/5O₄ y Li_1/2Fe_5/4Ce_5/4O₄.

Una temperatura más baja que la temperatura de Curie, pero en la que los momentos magnéticos opuestos son iguales (lo que resulta en un momento magnético neto de cero) se denomina punto de compensación de magnetización. Este punto de compensación se observa fácilmente en granates y aleaciones de metales de transición de tierras raras (RE-TM). Además, los ferrimagnetos también pueden tener un punto de compensación del momento angular, en el que desaparece el momento angular neto. Este punto de compensación es un punto crucial para lograr una inversión de magnetización de alta velocidad en dispositivos de memoria magnética.

Efecto de campos externos

Modelo teórico de magnetización

m

contra el campo magnético

h

. Empezando por el origen, la curva ascendente es la curva inicial de magnetización. La curva descendente después de la saturación, junto con la curva de retorno inferior, forman la bucle principal. Las interceptaciones

h c

m rs

son coercivity y saturation remanence.

Cuando las ferrimagnets están expuestas a un campo magnético externo, muestran lo que se llama histeresis magnética, donde el comportamiento magnético depende de la historia del imán. También exhiben una magnetización de saturación ${displaystyle M_{rs}}$ ; esta magnetización se alcanza cuando el campo externo es lo suficientemente fuerte para hacer que todos los momentos se alinean en la misma dirección. Cuando se alcanza este punto, la magnetización no puede aumentar ya que no hay más momentos para alinearse. Cuando se elimina el campo externo, la magnetización de la ferrimagnet no desaparecerá, pero seguirá existiendo una magnetización no cero. Este efecto se utiliza a menudo en aplicaciones de imanes. Si un campo externo en la dirección opuesta se aplica posteriormente, el imán desmagnetizará más hasta que finalmente llegue a una magnetización ${displaystyle -M_{rs}}$ . Este comportamiento resulta en lo que se llama hysteresis loop.

Propiedades y usos

Los materiales ferrimagnéticos tienen alta resistividad y propiedades anisotrópicas. La anisotropía en realidad es inducida por un campo externo aplicado. Cuando este campo aplicado se alinea con los dipolos magnéticos, provoca un momento dipolar magnético neto y provoca la precesión de los dipolos magnéticos a una frecuencia controlada por el campo aplicado, llamada Larmor o frecuencia de precesión. Como ejemplo particular, una señal de microondas polarizada circularmente en la misma dirección que esta precesión interactúa fuertemente con los momentos dipolares magnéticos; cuando está polarizado en dirección opuesta, la interacción es muy baja. Cuando la interacción es fuerte, la señal de microondas puede atravesar el material. Esta propiedad direccional se usa en la construcción de dispositivos de microondas como aisladores, circuladores y giradores. Los materiales ferrimagnéticos también se utilizan para producir circuladores y aisladores ópticos. Los minerales ferrimagnéticos en varios tipos de rocas se utilizan para estudiar las propiedades geomagnéticas antiguas de la Tierra y otros planetas. Ese campo de estudio se conoce como paleomagnetismo. Además, se ha demostrado que los ferriimanes como la magnetita se pueden utilizar para el almacenamiento de energía térmica.

Ejemplos

El material magnético más antiguo conocido, la magnetita, es una sustancia ferrimagnética. Los sitios tetraédricos y octaédricos de su estructura cristalina exhiben espín opuesto. Otros materiales ferrimagnéticos conocidos incluyen granate de hierro itrio (YIG); ferritas cúbicas compuestas de óxidos de hierro con otros elementos como aluminio, cobalto, níquel, manganeso y zinc; y ferritas hexagonales o de tipo espinela, incluidas la ferrita de renio, ReFe₂O₄, PbFe₁₂O₁₉ y BaFe ₁₂O₁₉ y pirrotita, Fe_1−xS.

El ferrimagnetismo también puede ocurrir en imanes de una sola molécula. Un ejemplo clásico es una molécula dodecanuclear de manganeso con un espín efectivo S = 10 derivado de la interacción antiferromagnética en centros metálicos Mn(IV) con centros metálicos Mn(III) y Mn(II).

Contenido relacionado

Más resultados...