Falacia del jugador
La falacia del jugador, también conocida como falacia de Montecarlo o falacia de la madurez de las posibilidades, es la creencia incorrecta de que, si un evento en particular ocurre con más frecuencia de lo normal durante el pasado, es menos probable que suceda en el futuro (o viceversa), cuando se ha establecido que la probabilidad de tales eventos no depende de lo que ha sucedido. sucedió en el pasado. Dichos eventos, que tienen la cualidad de la independencia histórica, se denominan estadísticamente independientes. La falacia se asocia comúnmente con los juegos de azar, donde se puede creer, por ejemplo, que la próxima tirada de dados es más probable que sea seis porque recientemente ha habido menos seises de los esperados.
El término "falacia de Montecarlo" tiene su origen en el ejemplo más conocido del fenómeno, ocurrido en el Casino de Montecarlo en 1913.
Ejemplos
Lanzamiento de moneda
La falacia del jugador se puede ilustrar considerando el lanzamiento repetido de una moneda justa. Los resultados en diferentes lanzamientos son estadísticamente independientes y la probabilidad de obtener cara en un solo lanzamiento es 1/2 (uno de cada dos). La probabilidad de obtener dos caras en dos lanzamientos es 1/4 (uno en cuatro) y la probabilidad de obtener tres caras en tres lanzamientos es 1/8 (uno de cada ocho). En general, si Ai es el evento en el que al lanzar i una moneda justa sale cara, entonces:
- Pr()⋂ ⋂ i=1nAi)=∏ ∏ i=1nPr()Ai)=12n{displaystyle Pr left(bigcap _{i=1}{n}A_{i}right)=prod ¿Por qué?.
Si después de lanzar cuatro caras seguidas, el siguiente lanzamiento de moneda también sale cara, completaría una serie de cinco caras sucesivas. Dado que la probabilidad de una serie de cinco caras sucesivas es 1/32 (uno de cada treinta y dos), una persona podría creer que en el siguiente lanzamiento es más probable que salga cruz en lugar de cara nuevamente. Esto es incorrecto y es un ejemplo de la falacia del jugador. El evento "5 cabezas seguidas" y el evento "primeras 4 caras, luego cruces" son igualmente probables, cada uno con probabilidad 1/32. Dado que los primeros cuatro lanzamientos arrojan cara, la probabilidad de que el siguiente lanzamiento sea cara es:
- Pr()A5SilencioA1∩ ∩ A2∩ ∩ A3∩ ∩ A4)=Pr()A5)=12{displaystyle Pr left(A_{5}PrincipadoA_{1}cap A_{2}cap A_{3}cap A_{4}right)=Pr left(A_{5}right)=frac {1}{2}}}.
Mientras que una racha de cinco caras tiene una probabilidad de 1 //span>32 = 0.03125 (un poco más del 3%), el malentendido radica en no darse cuenta de que esto es así solo antes de la primera se lanza la moneda. Después de los primeros cuatro lanzamientos en este ejemplo, los resultados ya no son desconocidos, por lo que sus probabilidades en ese punto son iguales a 1 (100%). La probabilidad de que una serie de lanzamientos de monedas de cualquier duración continúe durante un lanzamiento más es siempre 0,5. El razonamiento de que es más probable que un quinto lanzamiento sea cruz porque los cuatro lanzamientos anteriores fueron cara, con una racha de suerte en el pasado que influye en las probabilidades en el futuro, forma la base de la falacia.
Por qué la probabilidad es 1/2 para una moneda justa
Si se lanza una moneda justa 21 veces, la probabilidad de que salga 21 caras es de 1 en 2.097.152. La probabilidad de sacar una cara después de haber lanzado 20 caras seguidas es 1/2. Suponiendo una moneda justa:
- La probabilidad de 20 cabezas, luego 1 cola es 0,520 × 0,5 = 0,521
- La probabilidad de 20 cabezas, luego 1 cabeza es 0,520 × 0,5 = 0,521
La probabilidad de obtener 20 caras y luego 1 cruz, y la probabilidad de obtener 20 caras y luego otra cara son ambas de 1 en 2,097,152. Al lanzar una moneda al aire 21 veces, es igualmente probable que el resultado sea 21 caras que 20 caras y luego 1 cruz. Estos dos resultados son tan probables como cualquiera de las otras combinaciones que se pueden obtener de 21 lanzamientos de una moneda. Todas las combinaciones de 21 lanzamientos tendrán probabilidades iguales a 0.521, o 1 en 2,097,152. Suponer que se producirá un cambio en la probabilidad como resultado del resultado de lanzamientos anteriores es incorrecto porque cada resultado de una secuencia de 21 lanzamientos es tan probable como los demás resultados. De acuerdo con Bayes' teorema, el resultado probable de cada lanzamiento es la probabilidad de la moneda justa, que es 1/2.
Otros ejemplos
La falacia conduce a la noción incorrecta de que los fracasos anteriores crearán una mayor probabilidad de éxito en los intentos posteriores. Para un dado justo de 16 caras, la probabilidad de que ocurra cada resultado es 1/16 (6,25 %). Si una ganancia se define como sacar un 1, la probabilidad de que ocurra un 1 al menos una vez en 16 tiradas es:
- 1− − [1516]16=64.39% % {displaystyle 1-left[{frac {15}{16}right]{16},=,64.39%}
La probabilidad de perder en la primera tirada es 15 //span>16 (93,75 %). De acuerdo con la falacia, el jugador debería tener una mayor probabilidad de ganar después de que se haya producido una pérdida. La probabilidad de al menos una victoria es ahora:
- 1− − [1516]15=62.02% % {displaystyle 1-left[{frac {15}{16}right] 15},=,62.02%}
Al perder un lanzamiento, la probabilidad de ganar del jugador se reduce en dos puntos porcentuales. Con 5 pérdidas y 11 tiradas restantes, la probabilidad de ganar se reduce a alrededor de 0,5 (50%). La probabilidad de al menos una victoria no aumenta después de una serie de pérdidas; de hecho, la probabilidad de éxito en realidad disminuye, porque quedan menos intentos en los que ganar. La probabilidad de ganar eventualmente será igual a la probabilidad de ganar un solo lanzamiento, que es 1/16 (6,25 %) y ocurre cuando solo queda un lanzamiento.
Posición inversa
Después de una tendencia constante hacia las colas, un jugador también puede decidir que las colas se han convertido en un resultado más probable. Esta es una conclusión racional y bayesiana, teniendo en cuenta la posibilidad de que la moneda no sea justa; no es una falacia. Creyendo que las probabilidades favorecen a las cruces, el jugador no ve ninguna razón para cambiar a cara. Sin embargo, es una falacia que una secuencia de ensayos lleve un recuerdo de resultados pasados que tienden a favorecer o desfavorecer los resultados futuros.
La falacia del jugador inverso descrita por Ian Hacking es una situación en la que un jugador que ingresa a una habitación y ve a una persona que lanza un doble seis en un par de dados puede concluir erróneamente que la persona debe haber estado lanzando los dados durante bastante tiempo, ya que es poco probable que obtengan un doble seis en su primer intento.
La falacia del jugador retrospectivo
Los investigadores han examinado si existe un sesgo similar para las inferencias sobre eventos pasados desconocidos basados en eventos posteriores conocidos, lo que se denomina "falacia del jugador retrospectivo".
Un ejemplo de la falacia de un jugador retrospectivo sería observar múltiples "caras" en un lanzamiento de moneda y concluya de esto que el lanzamiento previamente desconocido fue 'cruz'. Se ha argumentado que existen ejemplos del mundo real de la falacia del jugador retrospectivo en eventos como el origen del Universo. En su libro Universos, John Leslie argumenta que "la presencia de muchísimos universos muy diferentes en sus caracteres podría ser nuestra mejor explicación de por qué al menos un universo tiene un carácter que permite la vida".;. Daniel M. Oppenheimer y Benoît Monin argumentan que "En otras palabras, la 'mejor explicación' para un evento de baja probabilidad es que es solo uno en un múltiplo de intentos, que es la intuición central de la falacia del jugador inverso. Los argumentos filosóficos están en curso sobre si tales argumentos son o no una falacia, argumentando que la ocurrencia de nuestro universo no dice nada sobre la existencia de otros universos o pruebas de universos. Tres estudios en los que participaron estudiantes de la Universidad de Stanford probaron la existencia de un estudio retrospectivo de jugadores. falacia. Los tres estudios concluyeron que las personas tienen un problema de los jugadores. falacia retrospectivamente, así como a eventos futuros. Los autores de los tres estudios concluyeron que sus hallazgos tienen importantes "implicaciones metodológicas" pero también puede tener "implicaciones teóricas importantes" que necesitan investigación e investigación, diciendo que "[una] comprensión profunda de tales procesos de razonamiento requiere que no solo examinemos cómo influyen en nuestras predicciones del futuro, sino también en nuestras percepciones del pasado".
Parto
En 1796, Pierre-Simon Laplace describió en Un ensayo filosófico sobre las probabilidades las formas en que los hombres calculaban su probabilidad de tener hijos varones: "He visto hombres ardientemente deseosos de tener una hijo, que sólo podía enterarse con ansiedad de los nacimientos de niños en el mes en que esperaban ser padres. Imaginando que la razón de estos nacimientos a los de niñas debía ser la misma al final de cada mes, juzgaron que los niños ya nacidos harían más probables los próximos nacimientos de niñas." Los futuros padres temían que si nacían más hijos en la comunidad circundante, entonces ellos mismos tendrían más probabilidades de tener una hija. Este ensayo de Laplace se considera una de las primeras descripciones de la falacia. Asimismo, después de tener varios hijos del mismo sexo, algunos padres pueden creer erróneamente que van a tener un hijo del sexo opuesto.
Casino de Montecarlo
Quizás el ejemplo más famoso de la falacia del jugador ocurrió en un juego de ruleta en el Casino de Montecarlo el 18 de agosto de 1913, cuando la bola cayó negra 26 veces seguidas. Esta fue una ocurrencia extremadamente poco común: la probabilidad de que una secuencia de rojo o negro ocurra 26 veces seguidas es (18/37)26-1 o alrededor de 1 en 66,6 millones, suponiendo que el mecanismo sea imparcial. Los jugadores perdieron millones de francos apostando contra el negro, razonando incorrectamente que la racha estaba provocando un desequilibrio en la aleatoriedad de la rueda y que tenía que ser seguida por una larga racha roja.
No-ejemplos
Eventos no independientes
La falacia del jugador no se aplica cuando la probabilidad de diferentes eventos no es independiente. En tales casos, la probabilidad de eventos futuros puede cambiar según el resultado de eventos pasados, como la permutación estadística de eventos. Un ejemplo es cuando se extraen cartas de un mazo sin reemplazo. Si se extrae un as de una baraja y no se reinserta, es menos probable que la siguiente carta extraída sea un as y más probable que sea de otro rango. La probabilidad de sacar otro as, asumiendo que fue la primera carta sacada y que no hay comodines, ha disminuido de 4/52 (7,69 %) a 3/51 (5,88 %), mientras que la probabilidad de cada rango ha aumentado de 4 //span>52 (7,69 %) a 4 /51 (7,84 %). Este efecto permite que los sistemas de conteo de cartas funcionen en juegos como el blackjack.
Sesgo
En la mayoría de las ilustraciones de la falacia del jugador y la falacia del jugador inverso, se supone que el juicio (por ejemplo, lanzar una moneda al aire) es justo. En la práctica, esta suposición puede no ser válida. Por ejemplo, si una moneda se lanza 21 veces, la probabilidad de que salga 21 caras con una moneda justa es de 1 en 2.097.152. Dado que esta probabilidad es tan pequeña, si sucede, bien puede ser que la moneda esté de alguna manera predispuesta a caer sobre cara, o que esté siendo controlada por imanes ocultos, o algo similar. En este caso, la apuesta inteligente es "cara" porque la inferencia bayesiana de la evidencia empírica (21 caras seguidas) sugiere que es probable que la moneda esté sesgada hacia las caras. La inferencia bayesiana se puede utilizar para mostrar que cuando la proporción a largo plazo de diferentes resultados es desconocida pero intercambiable (lo que significa que el proceso aleatorio a partir del cual se generan los resultados puede estar sesgado pero es igualmente probable que esté sesgado en cualquier dirección) y que las observaciones demuestran la dirección probable del sesgo, el resultado que más ha ocurrido en los datos observados es el que tiene más probabilidades de volver a ocurrir.
Por ejemplo, si la probabilidad a priori de una moneda sesgada es, digamos, del 1 %, y suponiendo que dicha moneda sesgada salga cara, digamos el 60 % de las veces, luego de 21 caras, la la probabilidad de una moneda sesgada ha aumentado a alrededor del 32%.
La escena de apertura de la obra Rosencrantz and Guildenstern Are Dead de Tom Stoppard analiza estos temas mientras un hombre continuamente cambia cabezas y el otro considera varias explicaciones posibles.
Probabilidades cambiantes
Si se permite que los factores externos cambien la probabilidad de los eventos, es posible que la falacia del jugador no se cumpla. Por ejemplo, un cambio en las reglas del juego podría favorecer a un jugador sobre el otro, mejorando su porcentaje de ganancias. Del mismo modo, el éxito de un jugador inexperto puede disminuir después de que los equipos contrarios conozcan y jueguen contra sus debilidades. Este es otro ejemplo de sesgo.
Psicología
Orígenes
La falacia del jugador surge de la creencia en una ley de los números pequeños, lo que lleva a la creencia errónea de que las muestras pequeñas deben ser representativas de la población más grande. De acuerdo con la falacia, las rachas eventualmente deben nivelarse para ser representativas. Amos Tversky y Daniel Kahneman propusieron por primera vez que la falacia del jugador es un sesgo cognitivo producido por una heurística psicológica llamada heurística de representatividad, que establece que las personas evalúan la probabilidad de un determinado evento evaluando qué tan similar es a los eventos que han tenido. experimentado antes, y qué tan similares son los eventos que rodean a esos dos procesos. De acuerdo con este punto de vista, 'después de observar una serie larga de rojo en la rueda de la ruleta, por ejemplo, la mayoría de la gente cree erróneamente que el negro resultará en una secuencia más representativa que la aparición de un rojo adicional', por lo que la gente espere que una serie corta de resultados aleatorios comparta las propiedades de una serie más larga, específicamente en que las desviaciones del promedio deberían equilibrarse. Cuando se les pide a las personas que inventen una secuencia aleatoria de lanzamientos de monedas, tienden a hacer secuencias en las que la proporción de caras y cruces se mantiene más cerca de 0,5 en cualquier segmento corto de lo que se predeciría por casualidad, un fenómeno conocido como insensibilidad a la muestra. Talla. Kahneman y Tversky interpretan que esto significa que la gente cree que las secuencias cortas de eventos aleatorios deberían ser representativas de las más largas. La heurística de representatividad también se cita detrás del fenómeno relacionado de la ilusión de agrupamiento, según el cual las personas ven las rachas de eventos aleatorios como no aleatorios cuando en realidad es mucho más probable que ocurran tales rachas en muestras pequeñas de lo que la gente espera.
La falacia del jugador también se puede atribuir a la creencia errónea de que el juego, o incluso el azar en sí mismo, es un proceso justo que puede corregirse por sí mismo en caso de rachas, lo que se conoce como la hipótesis del mundo justo. Otros investigadores creen que la creencia en la falacia puede ser el resultado de una creencia errónea en un locus de control interno. Cuando una persona cree que los resultados del juego son el resultado de su propia habilidad, puede ser más susceptible a la falacia del jugador porque rechaza la idea de que el azar pueda superar la habilidad o el talento.
Variaciones
Algunos investigadores creen que es posible definir dos tipos de falacia del jugador: tipo uno y tipo dos. El tipo uno es la clásica falacia del jugador, en la que las personas creen que se debe un resultado particular después de una larga racha de otro resultado. La falacia del jugador de tipo dos, tal como la definen Gideon Keren y Charles Lewis, ocurre cuando un jugador subestima cuántas observaciones se necesitan para detectar un resultado favorable, como mirar la rueda de la ruleta durante un período de tiempo y luego apostar en la misma. números que aparecen con mayor frecuencia. Para eventos con un alto grado de aleatoriedad, la detección de un sesgo que conducirá a un resultado favorable requiere una gran cantidad de tiempo y es muy difícil, si no imposible, de hacer. Los dos tipos difieren en que el tipo uno asume erróneamente que las condiciones de juego son justas y perfectas, mientras que el tipo dos supone que las condiciones están sesgadas y que este sesgo se puede detectar después de un cierto período de tiempo.
Otra variedad, conocida como la falacia del jugador retrospectivo, ocurre cuando las personas juzgan que un evento aparentemente raro debe provenir de una secuencia más larga que un evento más común. La creencia de que una secuencia imaginaria de tiradas de dados es más de tres veces más larga cuando se observa un conjunto de tres seises en comparación con cuando solo hay dos seises. Este efecto se puede observar en instancias aisladas, o incluso secuencialmente. Otro ejemplo implicaría escuchar que una adolescente tiene relaciones sexuales sin protección y queda embarazada en una noche determinada, y concluir que ha estado teniendo relaciones sexuales sin protección durante más tiempo que si escuchamos que tuvo relaciones sexuales sin protección pero no quedó embarazada, cuando la probabilidad de quedar embarazada embarazada como resultado de cada relación sexual es independiente de la cantidad de relaciones sexuales anteriores.
Relación con la falacia de la mano caliente
Otra perspectiva psicológica afirma que la falacia del jugador puede verse como la contraparte de la falacia de la mano caliente del baloncesto, en la que las personas tienden a predecir el mismo resultado que el evento anterior, conocido como actualidad positiva. dando como resultado la creencia de que un anotador alto seguirá anotando. En la falacia del jugador, las personas predicen el resultado opuesto del evento anterior, la actualidad negativa, creyendo que dado que la rueda de la ruleta ha caído en negro en las seis ocasiones anteriores, debe caer en rojo la siguiente. Ayton y Fischer han teorizado que las personas muestran una actualidad positiva para la falacia de la mano caliente porque la falacia se relaciona con el desempeño humano y que las personas no creen que un objeto inanimado pueda volverse "caliente". El desempeño humano no se percibe como aleatorio, y es más probable que las personas continúen con las rachas cuando creen que el proceso que genera los resultados no es aleatorio. Cuando una persona exhibe la falacia del jugador, es más probable que también presente la falacia de la mano caliente, lo que sugiere que una construcción es responsable de las dos falacias.
La diferencia entre las dos falacias también se encuentra en la toma de decisiones económicas. Un estudio realizado por Huber, Kirchler y Stockl en 2010 examinó cómo se exhiben la mano caliente y la falacia del jugador en el mercado financiero. Los investigadores dieron a elegir a sus participantes: podían apostar por el resultado de una serie de lanzamientos de monedas, usar la opinión de un experto para influir en su decisión o elegir una alternativa sin riesgo a cambio de una recompensa financiera más pequeña. Los participantes recurrieron a la opinión de expertos para tomar su decisión el 24% de las veces en función de su experiencia anterior de éxito, lo que ejemplifica la mano caliente. Si el experto estaba en lo cierto, el 78% de los participantes volvió a elegir la opinión del experto, frente al 57% que lo hizo cuando el experto estaba equivocado. Los participantes también exhibieron la falacia del jugador, con su selección de cara o cruz disminuyendo después de notar una racha de cualquiera de los resultados. Este experimento ayudó a reforzar la teoría de Ayton y Fischer de que las personas ponen más fe en el desempeño humano que en procesos aparentemente aleatorios.
Neurofisiología
Si bien la heurística de representatividad y otros sesgos cognitivos son las causas más citadas de la falacia del jugador, las investigaciones sugieren que también puede haber un componente neurológico. Las imágenes de resonancia magnética funcional han demostrado que después de perder una apuesta, lo que se conoce como riesgo de pérdida, la red frontoparietal del cerebro se activa, lo que da como resultado un comportamiento más arriesgado. Por el contrario, hay una disminución de la actividad en la amígdala, el caudado y el cuerpo estriado ventral después de una pérdida de riesgo. La activación en la amígdala se correlaciona negativamente con la falacia del jugador, de modo que cuanto mayor sea la actividad exhibida en la amígdala, menor será la probabilidad de que un individuo caiga presa de la falacia del jugador. Estos resultados sugieren que la falacia del jugador se basa más en la corteza prefrontal, que es responsable de los procesos ejecutivos dirigidos a objetivos, y menos en las áreas del cerebro que controlan la toma de decisiones afectivas.
El deseo de seguir jugando o apostando está controlado por el cuerpo estriado, que respalda un método de aprendizaje de contingencia de elección-resultado. El cuerpo estriado procesa los errores de predicción y el comportamiento cambia en consecuencia. Después de una victoria, se refuerza el comportamiento positivo y después de una pérdida, el comportamiento se condiciona para ser evitado. En las personas que exhiben la falacia del jugador, este método de contingencia de elección-resultado se ve afectado y continúan asumiendo riesgos después de una serie de pérdidas.
Posibles soluciones
La falacia del jugador es un sesgo cognitivo profundamente arraigado y puede ser muy difícil de superar. Educar a las personas sobre la naturaleza de la aleatoriedad no siempre ha demostrado ser eficaz para reducir o eliminar cualquier manifestación de la falacia. A los participantes en un estudio realizado por Beach y Swensson en 1967 se les mostró una baraja de fichas barajadas con formas en ellas, y se les indicó que adivinaran qué forma vendría a continuación en una secuencia. Se informó al grupo experimental de participantes sobre la naturaleza y la existencia de la falacia del jugador, y se les indicó explícitamente que no confiaran en la dependencia de ejecución para hacer sus conjeturas. El grupo de control no recibió esta información. Los estilos de respuesta de los dos grupos fueron similares, lo que indica que el grupo experimental aún basaba sus elecciones en la duración de la secuencia de ejecución. Esto llevó a la conclusión de que instruir a las personas sobre la aleatoriedad no es suficiente para disminuir la falacia del jugador.
La susceptibilidad de un individuo a la falacia del jugador puede disminuir con la edad. Un estudio realizado por Fischbein y Schnarch en 1997 administró un cuestionario a cinco grupos: estudiantes en los grados 5, 7, 9, 11 y estudiantes universitarios especializados en la enseñanza de las matemáticas. Ninguno de los participantes había recibido educación previa con respecto a la probabilidad. La pregunta que se hizo fue: 'Ronni lanzó una moneda al aire tres veces y en todos los casos salió cara. Ronni tiene la intención de lanzar la moneda de nuevo. ¿Cuál es la probabilidad de obtener cara la cuarta vez?" Los resultados indicaron que a medida que los estudiantes crecían, era menos probable que respondieran con 'menor que la probabilidad de obtener cruces', lo que indicaría un efecto de actualidad negativo. El 35 % de los alumnos de 5.º grado, el 35 % de los alumnos de 7.º grado y el 20 % de los alumnos de 9.º grado exhibieron el efecto de actualidad negativa. Solo el 10% de los estudiantes de 11.º grado respondieron de esta manera, y ninguno de los estudiantes universitarios lo hizo. Fischbein y Schnarch teorizaron que la tendencia de un individuo a confiar en la heurística de representatividad y otros sesgos cognitivos pueden superarse con la edad.
Otra posible solución proviene de Roney y Trick, psicólogos de la Gestalt que sugieren que la falacia puede eliminarse como resultado de la agrupación. Cuando un evento futuro, como el lanzamiento de una moneda, se describe como parte de una secuencia, sin importar cuán arbitrariamente, una persona automáticamente considerará el evento en relación con los eventos pasados, lo que resultará en la falacia del jugador. Cuando una persona considera cada evento como independiente, la falacia puede reducirse en gran medida.
Roney y Trick les dijeron a los participantes en su experimento que estaban apostando a dos bloques de seis lanzamientos de monedas oa dos bloques de siete lanzamientos de monedas. Los lanzamientos cuarto, quinto y sexto tuvieron el mismo resultado, ya sea tres caras o tres cruces. El séptimo lanzamiento se agrupó con el final de un bloque o el comienzo del siguiente bloque. Los participantes exhibieron la falacia del jugador más fuerte cuando la séptima prueba fue parte del primer bloque, directamente después de la secuencia de tres caras o cruces. Los investigadores señalaron que los participantes que no mostraron la falacia del jugador mostraron menos confianza en sus apuestas y apostaron menos veces que los participantes que eligieron con la falacia del jugador. Cuando el séptimo ensayo se agrupó con el segundo bloque y se percibió como no parte de una racha, la falacia del jugador no ocurrió.
Roney y Trick argumentaron que en lugar de enseñar a las personas sobre la naturaleza de la aleatoriedad, la falacia podría evitarse capacitando a las personas para que traten cada evento como si fuera el comienzo y no la continuación de eventos anteriores. Sugirieron que esto evitaría que las personas apuesten cuando están perdiendo, con la esperanza errónea de que sus posibilidades de ganar aumenten en función de una interacción con eventos anteriores.
Usuarios
Tipos de usuarios
Dentro de un entorno del mundo real, numerosos estudios han descubierto que para varios tomadores de decisiones ubicados en escenarios de alto riesgo, es probable que reflejen algún grado de fuerte autocorrelación negativa en su juicio.
Jueces de asilo
En un estudio destinado a descubrir si la autocorrelación negativa que existe con la falacia del jugador existía en la decisión tomada por los jueces de asilo de EE. UU., los resultados mostraron que después de dos otorgamientos de asilo sucesivos, un juez tendría un 5,5% menos para aprobar una tercera subvención.
Árbitros de béisbol
En el juego de béisbol, las decisiones se toman cada minuto. Una decisión particular tomada por los árbitros que a menudo está sujeta a escrutinio es la decisión de la "zona de strike". Cada vez que un bateador no hace el swing, el árbitro debe decidir si la bola estaba dentro de una región justa para el bateador, conocida como zona de strike. Si está fuera de esta zona, la bola no cuenta para sacar al bateador. En un estudio de más de 12.000 juegos, los resultados mostraron que los árbitros tienen un 1,3 % menos de probabilidades de pedir un strike si las dos bolas anteriores también fueron strikes.
Oficiales de crédito
En la toma de decisiones de los oficiales de crédito, se puede argumentar que los incentivos monetarios son un factor clave en la toma de decisiones sesgada, lo que dificulta examinar el efecto de falacia del jugador. Sin embargo, la investigación muestra que los oficiales de crédito que no están incentivados por ganancias monetarias tienen un 8% menos de probabilidades de aprobar un préstamo si aprobaron uno para el cliente anterior.
Jugadores de lotería
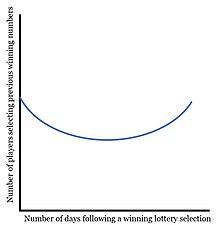
El juego de lotería y los botes atraen a los jugadores de todo el mundo, y la decisión más importante para los posibles ganadores es qué números elegir. Si bien la mayoría de las personas tendrán su propia estrategia, la evidencia muestra que después de que se selecciona un número como ganador en el sorteo actual, el mismo número experimentará una caída significativa en las selecciones en la siguiente lotería. Un estudio popular realizado por Charles Clotfelter y Philip Cook investigó este efecto en 1991, donde concluyeron que los apostadores dejarían de seleccionar números inmediatamente después de que fueran seleccionados, recuperando finalmente la popularidad de la selección en tres meses. Poco después, Dek Terrell construyó un estudio de 1994 para probar los hallazgos de Clotfelter y Cook. El cambio clave en el estudio de Terrell fue el examen de una lotería pari-mutuel en la que, un número seleccionado con apuestas totales más bajas dará como resultado un pago más alto. Si bien este examen concluyó que los jugadores en ambos tipos de lotería exhibieron un comportamiento en línea con la teoría de la falacia del jugador, aquellos que participaron en las apuestas mutuas parecían estar menos influenciados.
| Apostado por jugadores de lotería | ||||||
|---|---|---|---|---|---|---|
| Números sorteados 14 de abril de 1988 | Día del dibujo | Días después del sorteo | ||||
| Abril | Números ganadores | 0 | 1 | 3 | 7 | 56 |
| 11 | 244 | 41 | 34 | 24 | 27 | 30 |
| 12 | 504 | 29 | 20 | 12 | 18 | 15 |
| 13 | 718 | 28 | 20 | 17 | 19 | 25 |
| 14 | 323 | 134 | 95 | 79 | 81 | 76 |
| 15 | 640 | 10 | 20 | 18 | 16 | 20 |
| 16 | 957 | 30 | 22 | 20 | 24 | 32 |
| Porcentaje medio de jugadores seleccionando previamente
números ganadores en comparación con el día del sorteo | 78% | 63% | 68% | 73% | ||
El efecto de la falacia del jugador se puede observar cuando los números se eligen con mucha menos frecuencia poco después de que se seleccionan como ganadores, recuperándose lentamente durante un período de dos meses. Por ejemplo, el 11 de abril de 1988, 41 jugadores seleccionaron 244 como combinación ganadora. Tres días después, solo 24 individuos seleccionaron 244, una disminución del 41,5%. Esta es la falacia del jugador en movimiento, ya que los jugadores de lotería creen que la ocurrencia de una combinación ganadora en días anteriores disminuirá la probabilidad de que ocurra hoy.
Jugadores de videojuegos
Varios videojuegos cuentan con el uso de cajas de botín, una colección de elementos del juego que se otorgan al abrir con contenidos aleatorios establecidos por métricas de rareza, como esquema de monetización. Desde alrededor de 2018, las cajas de botín han sido objeto de escrutinio por parte de los gobiernos y los defensores sobre la base de que son similares a los juegos de azar, en particular para los juegos dirigidos a los jóvenes. Algunos juegos usan un "temporizador de lástima" mecanismo, que si el jugador ha abierto varias cajas de botín seguidas sin obtener un artículo de alta rareza, las cajas de botín subsiguientes mejorarán las probabilidades de que caiga un artículo de mayor tasa. Se considera que esto alimenta la falacia del jugador, ya que refuerza la idea de que un jugador eventualmente obtendrá un artículo de alta rareza (una ganancia) después de recibir solo artículos comunes de una serie de cajas de botín anteriores.
Contenido relacionado
Alegría
Ernesto jones
Hospital psiquiátrico



![1-left[frac{15}{16}right]^{16} ,=, 64.39%](https://wikimedia.org/api/rest_v1/media/math/render/svg/0d791f63cddc590830c6ef468bbf823c14c1953f)
![1-left[frac{15}{16}right]^{15} ,=, 62.02%](https://wikimedia.org/api/rest_v1/media/math/render/svg/1b0b7ce6d128c5742499914574afc8e625b73af1)