Factorización
En matemáticas, la factorización (o factorización, consulte diferencias ortográficas en inglés) o factorización consiste en escribir un número u otro objeto matemático como un producto de varios factores, generalmente objetos más pequeños o más simples del mismo tipo. Por ejemplo, 3 × 5 es una factorización del número entero 15, y (x – 2)(x + 2) es una factorización del polinomio x 2 – 4.
La factorización no suele considerarse significativa dentro de los sistemas de número que poseen división, como los números reales o complejos, ya que cualquier x{displaystyle x} puede ser trivialmente escrito como ()xSí.)× × ()1/Sí.){displaystyle (xy)times (1/y)} siempre Sí.{displaystyle y} no es cero. Sin embargo, una factorización significativa para un número racional o una función racional se puede obtener escribiendo en términos más bajos y factorando por separado su numerador y denominador.
La factorización fue considerada por primera vez por los antiguos matemáticos griegos en el caso de los números enteros. Demostraron el teorema fundamental de la aritmética, que afirma que todo número entero positivo puede descomponerse en un producto de números primos, que no pueden descomponerse en números enteros mayores que 1. Además, esta factorización es única hasta el orden de los factores. Aunque la factorización de enteros es una especie de inversa a la multiplicación, algorítmicamente es mucho más difícil, un hecho que se explota en el criptosistema RSA para implementar la criptografía de clave pública.
La factorización de polinomios también se ha estudiado durante siglos. En álgebra elemental, factorizar un polinomio reduce el problema de encontrar sus raíces a encontrar las raíces de los factores. Los polinomios con coeficientes en números enteros o en un campo poseen la propiedad de factorización única, una versión del teorema fundamental de la aritmética con números primos reemplazados por polinomios irreducibles. En particular, un polinomio univariante con coeficientes complejos admite una factorización única (hasta el orden) en polinomios lineales: esta es una versión del teorema fundamental del álgebra. En este caso, la factorización se puede hacer con algoritmos de búsqueda de raíces. El caso de polinomios con coeficientes enteros es fundamental para el álgebra computacional. Existen algoritmos informáticos eficientes para calcular factorizaciones (completas) dentro del anillo de polinomios con coeficientes de números racionales (ver factorización de polinomios).
Un anillo conmutativo que posee la propiedad de factorización única se denomina dominio de factorización única. Hay sistemas numéricos, como ciertos anillos de números enteros algebraicos, que no son dominios de factorización únicos. Sin embargo, los anillos de enteros algebraicos satisfacen la propiedad más débil de los dominios de Dedekind: los ideales se factorizan de forma única en los ideales primos.
Factorización también puede referirse a descomposiciones más generales de un objeto matemático en el producto de objetos más pequeños o más simples. Por ejemplo, cada función puede factorizarse en la composición de una función sobreyectiva con una función inyectiva. Las matrices poseen muchos tipos de factorizaciones de matrices. Por ejemplo, cada matriz tiene una factorización LUP única como producto de una matriz triangular inferior L con todas las entradas diagonales iguales a uno, una matriz triangular superior U, y una matriz de permutación P; esta es una formulación matricial de la eliminación gaussiana.
Enteros
De acuerdo con el teorema fundamental de la aritmética, todo número entero mayor que 1 tiene una factorización única (hasta el orden de los factores) en números primos, que son aquellos números enteros que no pueden factorizarse más en el producto de números enteros mayores que uno.
Para calcular la factorización de un número entero n, se necesita un algoritmo para encontrar un divisor q de n o decidir que n es primo. Cuando se encuentra dicho divisor, la aplicación repetida de este algoritmo a los factores q y n / q da finalmente la factorización completa de n.
Para encontrar un divisor q de n, si los hay, basta con probar todos los valores de q tales que 1 < q y q2 ≤ n. De hecho, si r es un divisor de n tal que r2 > n, luego q = n / r es un divisor de n tal que q2 ≤ n.
Si uno prueba los valores de q en orden creciente, el primer divisor que se encuentra es necesariamente un número primo, y el cofactor r = n / q no puede tener ninguna divisor menor que q. Para obtener la factorización completa, basta continuar con el algoritmo buscando un divisor de r que no sea menor que q y no mayor que √r.
No es necesario probar todos los valores de q para aplicar el método. En principio, es suficiente probar solo divisores primos. Esto necesita tener una tabla de números primos que se pueda generar por ejemplo con el tamiz de Eratóstenes. Como el método de factorización hace esencialmente el mismo trabajo que la criba de Eratóstenes, generalmente es más eficiente probar para un divisor solo aquellos números para los que no está claro de inmediato si son primos o no. Por lo general, se puede proceder probando 2, 3, 5 y los números > 5, cuyo último dígito es 1, 3, 7, 9 y la suma de los dígitos no es múltiplo de 3.
Este método funciona bien para factorizar números enteros pequeños, pero es ineficaz para números enteros más grandes. Por ejemplo, Pierre de Fermat no pudo descubrir que el sexto número de Fermat
- 1+225=1+232=4294967297{displaystyle 1+2^{2^{5}=1+2^{32}=4,294,967,297}
no es un número primo. De hecho, aplicar el método anterior requeriría más de 10000 divisiones, para un número que tiene 10 dígitos decimales.
Existen algoritmos de factorización más eficientes. Sin embargo, siguen siendo relativamente ineficientes, ya que, con el estado actual de la técnica, no se puede factorizar, incluso con las computadoras más poderosas, un número de 500 dígitos decimales que es el producto de dos números primos elegidos al azar. Esto garantiza la seguridad del sistema criptográfico RSA, que se usa ampliamente para la comunicación segura en Internet.
Ejemplo
Para factorizar n = 1386 en números primos:
- Comience con división para 2: el número es uniforme, y n = 2 = 693. Continuar con 693, y 2 como primer candidato divisor.
- 693 es raro (2 no es un divisor), pero es un múltiplo de 3: uno tiene 693 = 3 · 231 y n = 2 · 3 · 231. Continuar con 231, y 3 como primer candidato divisor.
- 231 es también un múltiple de 3: uno tiene 231 = 3 · 77, y así n = 2 · 32 · 77. Continuar con 77, y 3 como primer candidato divisor.
- 77 no es un múltiplo de 3, ya que la suma de sus dígitos es 14, no un múltiplo de 3. Tampoco es un múltiplo de 5 porque su último dígito es 7. El siguiente divisor extraño a ser probado es 7. Uno tiene 77 = 7 · 11, y así n = 2 · 32 · 7 · 11. Esto muestra que 7 es primo (fácil de probar directamente). Continuar con 11, y 7 como primer candidato divisor.
- As 72 ▪ 11Uno ha terminado. Así 11 es la primera, y la factorización principal es
- 1386 = 2 · 32 · 7 · 11.
Expresiones
La manipulación de expresiones es la base del álgebra. La factorización es uno de los métodos más importantes para la manipulación de expresiones por varias razones. Si uno puede poner una ecuación en forma factorizada E⋅F = 0, entonces el problema de resolver la ecuación se divide en dos problemas independientes (y generalmente más fáciles) E = 0 y F = 0 . Cuando una expresión se puede factorizar, los factores suelen ser mucho más simples y, por lo tanto, pueden ofrecer una idea del problema. Por ejemplo,
- x3− − ax2− − bx2− − cx2+abx+acx+bcx− − abc{displaystyle x^{3}-ax^{2}-bx^{2}-cx^{2}+abx+bcx-abcx}
que tiene 16 multiplicaciones, 4 restas y 3 sumas, puede factorizarse en la expresión mucho más simple
- ()x− − a)()x− − b)()x− − c),{displaystyle (x-a)(x-b)(x-c),}
con solo dos multiplicaciones y tres restas. Además, la forma factorizada da inmediatamente raíces x = a,b,c como raíces del polinomio.
Por otro lado, la factorización no siempre es posible, y cuando es posible, los factores no siempre son más simples. Por ejemplo, x10− − 1{displaystyle x^{10}-1} puede ser factorizado en dos factores irreducibles x− − 1{displaystyle x-1} y x9+x8+⋯ ⋯ +x2+x+1{displaystyle x^{9}+x^{8}+cdots +x^{2}+x+1}.
Se han desarrollado varios métodos para encontrar factorizaciones; algunos se describen a continuación.
La solución de ecuaciones algebraicas puede ser vista como un problema de la factorización polinomio. De hecho, el teorema fundamental del álgebra se puede decir como sigue: cada polinomio en x grado n con coeficientes complejos puede ser factorizado n factores lineales x− − ai,{displaystyle x-a_{i},} para i = 1,... n, donde el ais son las raíces del polinomio. Aunque la estructura de la factorización se conoce en estos casos, la ais generalmente no puede ser calculado en términos de radicales (nT raíces), por el teorema Abel-Ruffini. En la mayoría de los casos, lo mejor que se puede hacer es calcular valores aproximados de las raíces con un algoritmo de determinación de raíces.
Historia de la factorización de expresiones
El uso sistemático de manipulaciones algebraicas para simplificar expresiones (más específicamente ecuaciones) puede fecharse en el siglo IX, con el libro de al-Khwarizmi The Compendious Book on Calculation by Completion and Balancing, que se titula con dos tipos de manipulación.
Sin embargo, incluso para resolver ecuaciones cuadráticas, el método de factorización no se utilizó antes de que se publicara el trabajo de Harriot en 1631, diez años después de su muerte. En su libro Artis Analyticae Praxis ad Aequationes Algebraicas Resolvendas, Harriot dibujó tablas para sumar, restar, multiplicar y dividir monomios, binomios y trinomios. Luego, en una segunda sección, estableció la ecuación aa − ba + ca = + bc, y mostró que esto coincide con la forma de multiplicación que había proporcionado previamente, dando la factorización (a − b )(a + c).
Métodos generales
Los siguientes métodos se aplican a cualquier expresión que sea una suma o que pueda transformarse en una suma. Por lo tanto, se aplican con mayor frecuencia a polinomios, aunque también se pueden aplicar cuando los términos de la suma no son monomios, es decir, los términos de la suma son un producto de variables y constantes.
Factor común
Puede ocurrir que todos los términos de una suma sean productos y que algunos factores sean comunes a todos los términos. En este caso, la ley distributiva permite factorizar este factor común. Si hay varios factores comunes, es preferible dividir el mayor factor común. Además, si hay coeficientes enteros, se puede factorizar el máximo común divisor de estos coeficientes.
Por ejemplo,
- 6x3Sí.2+8x4Sí.3− − 10x5Sí.3=2x3Sí.2()3+4xSí.− − 5x2Sí.),{displaystyle 6x^{3}y^{2}+8x^{4}y^{3}-10x^{5}y^{3}=2x^{3}y^{2}(3+4xy-5x^{2}y),}
ya que 2 es el mayor divisor común de 6, 8, y 10, y x3Sí.2{displaystyle x^{3}y^{2} divide todos los términos.
Agrupación
La agrupación de términos puede permitir el uso de otros métodos para obtener una factorización.
Por ejemplo, para factorizar
- 4x2+20x+3xSí.+15Sí.,{displaystyle 4x^{2}+20x+3xy+15y,}
se puede comentar que los dos primeros términos tienen un factor común x, y los dos últimos términos tienen el factor común y. De este modo
- 4x2+20x+3xSí.+15Sí.=()4x2+20x)+()3xSí.+15Sí.)=4x()x+5)+3Sí.()x+5).{displaystyle 4x^{2}+20x+3xy+15y=(4x^{2}+20x)+(3xy+15y)=4x(x+5)+3y(x+5). }
Luego, una simple inspección muestra el factor común x + 5, lo que lleva a la factorización
- 4x2+20x+3xSí.+15Sí.=()4x+3Sí.)()x+5).{displaystyle 4x^{2}+20x+3xy+15y=(4x+3y)(x+5). }
En general, esto funciona para sumas de 4 términos que se han obtenido como producto de dos binomios. Aunque no con frecuencia, esto también puede funcionar para ejemplos más complicados.
Sumar y restar términos
A veces, alguna agrupación de términos revela parte de un patrón reconocible. Entonces es útil sumar y restar términos para completar el patrón.
Un uso típico de esto es el método de completar el cuadrado para obtener la fórmula cuadrática.
Otro ejemplo es la factorización de x4+1.{displaystyle x^{4}+1.} Si uno introduce la raíz cuadrada no real de –1, comúnmente denotado i, entonces uno tiene una diferencia de cuadrados
- x4+1=()x2+i)()x2− − i).{displaystyle x^{4}+1=(x^{2}+i)(x^{2}-i). }
Sin embargo, también se puede desear una factorización con coeficientes de número real. Añadiendo y restando 2x2,{displaystyle 2x^{2},} y agrupar tres términos juntos, uno puede reconocer el cuadrado de un binomio:
- x4+1=()x4+2x2+1)− − 2x2=()x2+1)2− − ()x2)2=()x2+x2+1)()x2− − x2+1).{2}+0}cH00}cH00cH00}cH00cH00cH00}cH00}ccH00}cH00}cH00}cH00}cH00}cH00cH00}cH00}cH009cH00cH00}cH009cH00cH00}cH009cH00}cH009cH00}cH009cH009cH00}cH00}cH009cH009cH00}cH00}cH00}cH009cH009cH00}cH00}cH00}cH00}cH009cH00}cH00}cH00}cH009}cH009cH009cH00}cH009}cH009c }
Subtracting and adding 2x2{displaystyle 2x^{2} también produce la factorización:
- x4+1=()x4− − 2x2+1)+2x2=()x2− − 1)2+()x2)2=()x2+x− − 2− − 1)()x2− − x− − 2− − 1).{2}+2}=(x^{2}==)}+left(x{2}sqrt {2}right)}{2}=left(x{2}sqrt {2}right)}{2}=left(x{2}+x{sq}{2}{2}{2}}{2}}left(x}}=======
Estas factorizaciones funcionan no sólo sobre los números complejos, sino también sobre cualquier campo, donde –1, 2 o –2 es un cuadrado. En un campo finito, el producto de dos no cuadrado es un cuadrado; esto implica que el polinomio x4+1,{displaystyle x^{4}+1,} que es irreducible sobre los enteros, es modulo reducible cada número primo. Por ejemplo,
- x4+1↑ ↑ ()x+1)4()mod2);{displaystyle x^{4}+1equiv (x+1)^{4}{pmod {2}}
- x4+1↑ ↑ ()x2+x− − 1)()x2− − x− − 1)()mod3),{displaystyle x^{4}+1equiv (x^{2}+x-1)(x^{2}-x-1){pmod {3}},qquad }desde entonces 12↑ ↑ − − 2()mod3);{displaystyle 1^{2}equiv -2{pmod {3}}
- x4+1↑ ↑ ()x2+2)()x2− − 2)()mod5),{displaystyle x^{4}+1equiv (x^{2}+2)(x^{2}-2){pmod {5}}qquad}desde entonces 22↑ ↑ − − 1()mod5);{displaystyle 2^{2}equiv -1{pmod {5}}
- x4+1↑ ↑ ()x2+3x+1)()x2− − 3x+1)()mod7),{displaystyle x^{4}+1equiv (x^{2}+3x+1)(x^{2}-3x+1){pmod {7}},qquad }desde entonces 32↑ ↑ 2()mod7).{displaystyle 3^{2}equiv 2{pmod {7}}
Patrones reconocibles
Muchas identidades proporcionan una igualdad entre una suma y un producto. Los métodos anteriores pueden usarse para dejar que el lado de la suma de alguna identidad aparezca en una expresión, que por lo tanto puede ser reemplazada por un producto.
Abajo están las identidades cuyos lados izquierdos se usan comúnmente como patrones (esto significa que las variables E y F que aparecen en estas identidades pueden representar cualquier subexpresión de la expresión que debe factorizarse).
- Diferencia de dos plazas
- E2− − F2=()E+F)()E− − F){displaystyle E^{2}-F^{2}=(E+F)(E-F)}
- Por ejemplo,
- a2+2ab+b2− − x2+2xSí.− − Sí.2=()a2+2ab+b2)− − ()x2− − 2xSí.+Sí.2)=()a+b)2− − ()x− − Sí.)2=()a+b+x− − Sí.)()a+b− − x+Sí.).{fnMicrosoft Sans Serif} {fnMicrosoft Sans Serif}]b} {2}+2}2}\2}\\=(a^{2}+2ab+b})-(x^{2}-2xy+y^{2})=cb} {cH0}
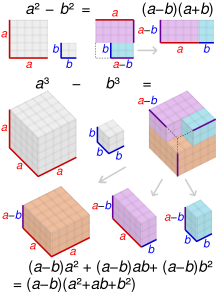
- Suma/diferencia de dos cubos
- E3+F3=()E+F)()E2− − EF+F2){displaystyle E^{3}+F^{3}=(E+F)(E^{2}-EF+F^{2}}
- E3− − F3=()E− − F)()E2+EF+F2){displaystyle E^{3}-F^{3}=(E-F)(E^{2}+EF+F^{2}}
- Diferencia de dos poderes cuarto
- E4− − F4=()E2+F2)()E2− − F2)=()E2+F2)()E+F)()E− − F){displaystyle {begin{aligned}E^{4}-F^{4} limit=(E^{2}+F^{2})(E^{2}-F^{2})\\ {2}+F^{2})(E+F)(E+F)end{aligned}}}}}}}}}}}
- Suma/diferencia de dos npoderes
- En las siguientes identidades, es posible que los factores se tengan más en cuenta:
- Diferencia, incluso exponente
- E2n− − F2n=()En+Fn)()En− − Fn){displaystyle E^{2n}-F^{2n}=(E^{n}+F^{n})(E^{n}-F^{n}}
- Diferencia, incluso o exponente extraño
- En− − Fn=()E− − F)()En− − 1+En− − 2F+En− − 3F2+⋯ ⋯ +EFn− − 2+Fn− − 1){displaystyle E^{n}-F^{n}=(E-F)(E^{n-1}+E^{n-2}F+E^{n-3}F^{2}+cdots +EF^{n-2}+F^{n-1}}
- Este es un ejemplo que muestra que los factores pueden ser mucho mayores que la suma que se factoriza.
- Sum, extraño exponente
- En+Fn=()E+F)()En− − 1− − En− − 2F+En− − 3F2− − ⋯ ⋯ − − EFn− − 2+Fn− − 1){displaystyle E^{n}+F^{n}=(E+F)(E^{n-1}-E^{n-2}F+E^{n-3}F^{2}-cdots - ¿Qué?
- (obtenido por cambiar F por –F en la fórmula anterior)
- Sum, incluso exponente
- Si el exponente es un poder de dos entonces la expresión no puede, en general, ser factorizada sin introducir números complejos (si E y F contener números complejos, esto puede no ser el caso). Si n tiene un divisor extraño, eso es si n = pq con p extraño, se puede utilizar la fórmula anterior (en "Sum, exponente impar") aplicada a ()Eq)p+()Fq)p.{displaystyle (E^{q})^{p}+(F^{q} {p}
- Trinomios y fórmulas cúbicas
- x2+Sí.2+z2+2()xSí.+Sí.z+xz)=()x+Sí.+z)2x3+Sí.3+z3− − 3xSí.z=()x+Sí.+z)()x2+Sí.2+z2− − xSí.− − xz− − Sí.z)x3+Sí.3+z3+3x2()Sí.+z)+3Sí.2()x+z)+3z2()x+Sí.)+6xSí.z=()x+Sí.+z)3x4+x2Sí.2+Sí.4=()x2+xSí.+Sí.2)()x2− − xSí.+Sí.2).{displaystyle {begin{aligned} {2}+y^{2}+z^{2}+2(xy+yz+xz)=(x+y+z)^{2}\\3}+y^{3}+z^{3}-3xyz=(x+y+z) (x=x){2}+x}{2}=x} {2})}+i}
- Expansiones binomiales
- El teorema binomio suministra patrones que se pueden reconocer fácilmente de los enteros que aparecen en ellos
- En grado bajo:
- a2+2ab+b2=()a+b)2{displaystyle a^{2}+2ab+b^{2}=(a+b)^{2}
- a2− − 2ab+b2=()a− − b)2{displaystyle a^{2}-2ab+b^{2}=(a-b)}{2}
- a3+3a2b+3ab2+b3=()a+b)3{displaystyle a^{3}+3a^{2}b+3ab^{2}+b^{3}=(a+b)^{3}
- a3− − 3a2b+3ab2− − b3=()a− − b)3{displaystyle a^{3}-3a^{2}b+3ab^{2}-b^{3}=(a-b)^{3}}
- Más generalmente, los coeficientes de las formas ampliadas de ()a+b)n{displaystyle (a+b)} {n} y ()a− − b)n{displaystyle (a-b)} {n} son los coeficientes binomiales, que aparecen en nla fila del triángulo de Pascal.
Raíces de unidad
El nlas raíces de la unidad son los números complejos cada uno de los cuales es una raíz del polinomio xn− − 1.{displaystyle x^{n}-1.} Son así los números
- e2ikπ π /n=# 2π π kn+ipecado 2π π kn{displaystyle e^{2ikpi - ¿Por qué? {2ccH00} ################################################################################################################################################################################################################################################################ {2ccH00} K} {n}}
para k=0,...... ,n− − 1.{displaystyle k=0,ldotsn-1.}
Se sigue que para cualquiera de las dos expresiones E y F, uno tiene:
- En− − Fn=()E− − F)∏ ∏ k=1n− − 1()E− − Fe2ikπ π /n){displaystyle E^{n}-F^{n}=(E-F)prod ¿Por qué?
- En+Fn=∏ ∏ k=0n− − 1()E− − Fe()2k+1)iπ π /n)sinIncluso{displaystyle E^{n}+F^{n}=prod ¿Por qué?
- En+Fn=()E+F)∏ ∏ k=1n− − 1()E+Fe2ikπ π /n)sinEs extraño.{displaystyle E^{n}+F^{n}=(E+F)prod ¿Por qué?
Si E y F son expresiones reales, y uno quiere factores reales, uno tiene que reemplazar cada par de factores complejos conjugados por su producto. Como complejo conjugado de eiα α {displaystyle e^{ialpha } es e− − iα α ,{displaystyle e^{-ialpha},} y
- ()a− − beiα α )()a− − be− − iα α )=a2− − ab()eiα α +e− − iα α )+b2eiα α e− − iα α =a2− − 2ab#α α +b2,{displaystyle left(a-be^{ialpha }right)left(a-be^{-ialpha }right)=a^{2}-ableft(e^{ialpha }+e^{-ialpha }right)+b^{2}e^{ialpha }e^{-ialpha }=a^{2}-2abcos ,alpha +b^{2}
uno tiene las siguientes factorizaciones reales (uno pasa de uno a otro cambiando k en n – k o n + 1 – k, y aplicando las fórmulas trigonométricas habituales:
- E2n− − F2n=()E− − F)()E+F)∏ ∏ k=1n− − 1()E2− − 2EF#kπ π n+F2)=()E− − F)()E+F)∏ ∏ k=1n− − 1()E2+2EF#kπ π n+F2){displaystyle {begin{aligned}E^{2n}-F^{2n} limit=(E-F)(E+F)prod ################################################################################################################################################################################################################################################################ Fcos ,{tfrac {kpi } {n}+F^{2}derecha)\\cH003(E-F)(E+F)prod ¿Por qué? - Bien.
- E2n+F2n=∏ ∏ k=1n()E2+2EF#()2k− − 1)π π 2n+F2)=∏ ∏ k=1n()E2− − 2EF#()2k− − 1)π π 2n+F2){displaystyle {begin{aligned}E^{2n}+F^{2n} ¿Qué? (E^{2}+2EFcos ,{tfrac {(2k-1)pi ### {2n}+F^{2}derecha]\fnMicrosoft Sans Serif} ¿Qué? (E^{2}-2EFcos ,{tfrac {(2k-1)pi {2n}f}f}f}end{aligned}}
Los cosenos que aparecen en estas factorizaciones son números algebraicos y pueden expresarse en términos de radicales (esto es posible porque su grupo de Galois es cíclico); sin embargo, estas expresiones radicales son demasiado complicadas para usarse, excepto por los valores bajos de n. Por ejemplo,
- a4+b4=()a2− − 2ab+b2)()a2+2ab+b2).{displaystyle a^{4}+b^{4}=(a^{2}-{sqrt {2}ab+b^{2})(a^{2}+{sqrt {2}ab+b^{2}). }
- a5− − b5=()a− − b)()a2+1− − 52ab+b2)()a2+1+52ab+b2),{displaystyle a^{5}-b^{5}=(a-b)left(a^{2}+{frac {1-{sqrt {5}} {2}}ab+b^{2}right)left(a^{2}+{frac} {1+{sqrt {5}} {2}}ab+b} {2}derecho),}
- a5+b5=()a+b)()a2− − 1− − 52ab+b2)()a2− − 1+52ab+b2),{displaystyle a^{5}+b^{5}=(a+b)left(a^{2}-{frac {1-{sqrt {5}} {2}}ab+b^{2}right)left(a^{2}-{frac} {1+{sqrt {5}} {2}}ab+b^{2}right),}
A menudo uno quiere una factorización con coeficientes racionales. Tal factorización implica polinomios ciclotómicos. Para expresar las factorizaciones racionales de sumas y diferencias o poderes, necesitamos una notación para la homogeneización de un polinomio: si P()x)=a0xn+aixn− − 1+⋯ ⋯ +an,{displaystyle P(x)=a_{0}x^{n}+a_{i}x^{n-1}+cdots # su homogeneización es el polinomio bivariado P̄ ̄ ()x,Sí.)=a0xn+aixn− − 1Sí.+⋯ ⋯ +anSí.n.{displaystyle {overline {}(x,y)=a_{0}x^{n}+a_{i}x^{n-1}y+cdots - Sí. Entonces, uno tiene
- En− − Fn=∏ ∏ k▪ ▪ nQ̄ ̄ n()E,F),{displaystyle E^{n}-F^{n}=prod ¿Qué? {}_{n}(E,F),}
- En+Fn=∏ ∏ k▪ ▪ 2n,k∤nQ̄ ̄ n()E,F),{displaystyle E^{n}+F^{n}=prod _{kmid 2n,knot mid n}{overline {}_{n}(E,F),}
donde los productos se toman sobre todos los divisores de n, o todos los divisores de 2n que no dividen n, y Qn()x){displaystyle Q_{n}(x)} es npolinomio ciclotómico.
Por ejemplo,
- a6− − b6=Q̄ ̄ 1()a,b)Q̄ ̄ 2()a,b)Q̄ ̄ 3()a,b)Q̄ ̄ 6()a,b)=()a− − b)()a+b)()a2− − ab+b2)()a2+ab+b2),{fnMicrosoft Sans Serif} {fnMicrosoft Sans Serif} {fnMicrosoft Sans Serif} {c] {fnMicrosoft Sans Serif} {fnMicrosoft Sans Serif} {fnMicrosoft Sans Serif} {fnMicrosoft Sans Serif} {b} {b}} {b} {b}}}} {b}}}}} {b} {b}}}} {b}}}} {b}}}}}}}}}}}} {b}}}} {b}}}}}}}}} {b}}}}}} {b} {b}}}} {b}}} {ccccccccb} {b} {cccccb} {ccccccb}}}}}}}}}
- a6+b6=Q̄ ̄ 4()a,b)Q̄ ̄ 12()a,b)=()a2+b2)()a4− − a2b2+b4),{displaystyle a^{6}+b^{6}={overline {Q}_{4}(a,b){overline {Q}_{12}(a,b)=(a^{2}+b^{2})(a^{4}-a^{2}b^{2}+b^{4}),}
ya que los divisores de 6 son 1, 2, 3, 6, y los divisores de 12 que no dividen a 6 son 4 y 12.
Polinomios
Para polinomios, la factorización está fuertemente relacionada con el problema de resolver ecuaciones algebraicas. Una ecuación algebraica tiene la forma
- P()x)=defa0xn+a1xn− − 1+⋯ ⋯ +an=0,{displaystyle P(x)\,{f} {f}fnMicrosoft Sans Serif} {fnMicrosoft Sans Serif} ,a_{0}x^{n}+a_{1}x^{n-1}+cdots #
Donde P()x) es un polinomio en x con a0ل ل 0.{displaystyle a_{0}neq 0.}Una solución de esta ecuación (también llamada raíz del polinomio) es un valor r de x tales que
- P()r)=0.{displaystyle P(r)=0.}
Si P()x)=Q()x)R()x){displaystyle P(x)=Q(x)R(x)} es una factorización de P()x) = 0 como producto de dos polinomios, luego las raíces de P()x) son la unión de las raíces de Q()x) y las raíces de R()x). Así resolver P()x) = 0 se reduce a los problemas más simples de resolver Q()x) = 0 y R()x) = 0.
Por el contrario, el teorema del factor afirma que, si r es una raíz de P(x) = 0, entonces P(x) se puede factorizar como
- P()x)=()x− − r)Q()x),{displaystyle P(x)=(x-r)Q(x),}
donde Q(x) es el cociente de la división euclidiana de P(x) = 0 por el factor lineal (grado uno) x – r.
Si los coeficientes de P(x) son números reales o complejos, el teorema fundamental del álgebra afirma que P(x) tiene una raíz real o compleja. Usando el teorema del factor recursivamente, resulta que
- P()x)=a0()x− − r1)⋯ ⋯ ()x− − rn),{displaystyle P(x)=a_{0}(x-r_{1})cdots (x-r_{n}),}
Donde r1,...... ,rn{displaystyle r_{1},ldotsr_{n} son las raíces reales o complejas de P, con algunos de ellos posiblemente repetidos. Esta factorización completa es única hasta el orden de los factores.
Si los coeficientes de P(x) son reales, generalmente se desea una factorización donde los factores tengan coeficientes reales. En este caso, la factorización completa puede tener algunos factores cuadráticos (grado dos). Esta factorización se puede deducir fácilmente de la factorización completa anterior. De hecho, si r = a + ib es una raíz no real de P(x), entonces su complejo conjugado s = a - ib también es una raíz de P(x). Entonces, el producto
- ()x− − r)()x− − s)=x2− − ()r+s)x+rs=x2− − 2ax+a2+b2{displaystyle (x-r)(x-s)=x^{2}-(r+s)x+rs=x^{2}-2ax+a^{2}+b^{2}
es un factor de P(x) con coeficientes reales. Repitiendo esto para todos los factores no reales da una factorización con factores reales lineales o cuadráticos.
Para calcular estas factorizaciones reales o complejas, se necesitan las raíces del polinomio, que pueden no calcularse exactamente y solo aproximarse mediante algoritmos de búsqueda de raíces.
En la práctica, la mayoría de las ecuaciones algebraicas de interés tienen coeficientes enteros o racionales, y es posible que desee una factorización con factores del mismo tipo. El teorema fundamental de la aritmética se puede generalizar a este caso, afirmando que los polinomios con coeficientes enteros o racionales tienen la propiedad de factorización única. Más precisamente, todo polinomio con coeficientes racionales se puede factorizar en un producto
- P()x)=qP1()x)⋯ ⋯ Pk()x),{displaystyle P(x)=q,P_{1}(x)cdots P_{k}(x),}
Donde q es un número racional y P1()x),...... ,Pk()x){displaystyle P_{1}(x),ldotsP_{k}(x)} son polinomios no constantes con coeficientes enteros que son irreducibles y primitivos; esto significa que ninguno de los Pi()x){displaystyle P_{i}(x)} puede ser escrito como el producto dos polinomios (con coeficientes enteros) que no son ni 1 ni –1 (los números enteros se consideran como polinomios de grado cero). Además, esta factorización es única hasta el orden de los factores y los signos de los factores.
Existen algoritmos eficientes para calcular esta factorización, que se implementan en la mayoría de los sistemas de álgebra computacional. Ver Factorización de polinomios. Desafortunadamente, estos algoritmos son demasiado complicados para usar en cálculos con papel y lápiz. Además de las heurísticas anteriores, solo unos pocos métodos son adecuados para los cálculos manuales, que generalmente funcionan solo para polinomios de bajo grado, con pocos coeficientes distintos de cero. Los principales métodos de este tipo se describen en las siguientes subsecciones.
Parte primitiva & factorización de contenido
Todo polinomio con coeficientes racionales, puede factorizarse, de forma única, como el producto de un número racional y un polinomio con coeficientes enteros, lo cual es primitivo (es decir, el máximo común divisor de los coeficientes es 1), y tiene un coeficiente principal positivo (coeficiente del término de mayor grado). Por ejemplo:
- − − 10x2+5x+5=()− − 5)⋅ ⋅ ()2x2− − x− − 1){displaystyle -10x^{2}+5x+5=(-5)cdot (2x^{2}-x-1)}
- 13x5+72x2+2x+1=16()2x5+21x2+12x+6){displaystyle {frac}{5}+{frac} {7}{2}x^{2}+2x+1={frac {1}{6}(2x^{5}+21x^{2}+12x+6)}
En esta factorización, el número racional se llama el contenido, y el polinomio primitivo es la parte primitiva. La computación de esta factorización puede hacerse de la siguiente manera: primero, reducir todos los coeficientes a un denominador común, para obtener el cociente por un entero q de un polinomio con coeficientes enteros. Entonces uno divide el divisor común mayor p de los coeficientes de este polinomio para obtener la parte primitiva, siendo el contenido p/q.{displaystyle p/q.} Finalmente, si es necesario, uno cambia los signos de p y todos los coeficientes de la parte primitiva.
Esta factorización puede producir un resultado mayor que el polinomio original (por lo general, cuando hay muchos denominadores coprimos), pero, incluso cuando este es el caso, la parte primitiva generalmente es más fácil de manipular para una mayor factorización.
Usando el teorema del factor
El teorema del factor establece que, si r es una raíz de un polinomio
- P()x)=a0xn+a1xn− − 1+⋯ ⋯ +an− − 1x+an,{displaystyle P(x)=a_{0}x^{n}+a_{1}x^{n-1}+cdots +a_{n-1}x+a_{n}
significa P(r) = 0, entonces hay una factorización
- P()x)=()x− − r)Q()x),{displaystyle P(x)=(x-r)Q(x),}
dónde
- Q()x)=b0xn− − 1+⋯ ⋯ +bn− − 2x+bn− − 1,{displaystyle Q(x)=b_{0}x^{n-1}+cdots +b_{n-2}x+b_{n-1},}
con a0=b0{displaystyle A_{0}=b_{0}. Luego división larga polinomio o división sintética dan:
- bi=a0ri+⋯ ⋯ +ai− − 1r+aiparai=1,...... ,n− − 1.{displaystyle b_{i}=a_{0}r^{i}+cdots +a_{i-1}r+a_{i} {fnMicrosoft Sans Serif} i=1,ldotsn{-}1.}
Esto puede ser útil cuando uno sabe o puede adivinar una raíz del polinomio.
Por ejemplo, P()x)=x3− − 3x+2,{displaystyle P(x)=x^{3}-3x+2,} se puede ver fácilmente que la suma de sus coeficientes es 0, por lo que r = 1 es una raíz. As r + 0 = 1, y r2+0r− − 3=− − 2,{displaystyle r^{2}+0r-3=-2,} uno tiene
- x3− − 3x+2=()x− − 1)()x2+x− − 2).{displaystyle x^{3}-3x+2=(x-1)(x^{2}+x-2). }
Raíces racionales
Para polinomios con coeficientes de números racionales, se pueden buscar raíces que sean números racionales. La factorización de contenido parcial primitivo (ver arriba) reduce el problema de buscar raíces racionales al caso de polinomios con coeficientes enteros que no tienen un divisor común no trivial.
Si x=pq{displaystyle x={tfrac {} {}}} es una raíz racional de tal polinomio
- P()x)=a0xn+a1xn− − 1+⋯ ⋯ +an− − 1x+an,{displaystyle P(x)=a_{0}x^{n}+a_{1}x^{n-1}+cdots +a_{n-1}x+a_{n}
el teorema del factor muestra que uno tiene una factorización
- P()x)=()qx− − p)Q()x),{displaystyle P(x)=(qx-p)Q(x),}
donde ambos factores tienen coeficientes enteros (el hecho de que Q tiene coeficientes enteros resultados de la fórmula anterior para el cociente de P()x) por x− − p/q{displaystyle x-p/q}).
Comparación de los coeficientes de grado n y los coeficientes constantes en la igualdad anterior muestran que, si pq{fnMicroc} {} {}}} es una raíz racional en forma reducida, entonces q es un divisor de a0,{displaystyle a_{0},} y p es un divisor de an.{displaystyle a. Por lo tanto, hay un número finito de posibilidades para p y q, que se puede examinar sistemáticamente.
Por ejemplo, si el polinomio
- P()x)=2x3− − 7x2+10x− − 6{displaystyle P(x)=2x^{3}-7x^{2}+10x-6}
tiene una raíz racional pq{fnMicroc} {} {}}} con q ■ 0, entonces p debe dividir 6; es decir, p▪ ▪ {}± ± 1,± ± 2,± ± 3,± ± 6},{displaystyle pin {pm 1,pm 2,pm 3,pm 6} y q debe dividir 2, es decir, q▪ ▪ {}1,2}.{displaystyle qin {1,2} Además, si x 0, todos los términos del polinomio son negativos, y, por lo tanto, una raíz no puede ser negativa. Es decir, uno debe tener
- pq▪ ▪ {}1,2,3,6,12,32}.{displaystyle {tfrac {fn}in} {1,2,3,6, {tfrac}{2}} {tfrac} {3}{2}}}
Un cálculo directo muestra que sólo 32{fnMicroc} {3}{2}} es una raíz, por lo que no puede haber otra raíz racional. Aplicar el teorema factor conduce finalmente a la factorización 2x3− − 7x2+10x− − 6=()2x− − 3)()x2− − 2x+2).{displaystyle 2x^{3}-7x^{2}+10x-6=(2x-3)(x^{2}-2x+2). }
Método ac cuadrático
El método anterior se puede adaptar para polinomios cuadráticos, lo que lleva al método ac de factorización.
Considere el polinomio cuadrático
- P()x)=ax2+bx+c{displaystyle P(x)=ax^{2}+bx+c}
con coeficientes enteros. Si tiene una raíz racional, su denominador debe dividir a uniformemente y puede ser escrito como una posible fracción reducible r1=ra.{displaystyle r_{1}={tfrac {} {}}} Por las fórmulas de Vieta, la otra raíz r2{displaystyle R_{2} es
- r2=− − ba− − r1=− − ba− − ra=− − b+ra=sa,{displaystyle r_{2}=-{frac {B}}-r_{1}=-{frac {b}{a}-{frac} {}=-{f} {B+R} {fnK}={frac} {} {}}}
con s=− − ()b+r).{displaystyle s=-(b+r).}Así la segunda raíz es también racional, y la segunda fórmula de Vieta r1r2=ca{displaystyle r_{1}r_{2}={frac {c}{a}} da
- sara=ca,{displaystyle {frac}{frac} {fnMicroc}} {fnMicroc}}} {f}}} {fn}}}} {fnMicroc}} {fnMicroc}}}} {f}}}}} {f}} {} {fn}={fnMic} {c}{a}},}
eso es
- rs=acyr+s=− − b.{displaystyle rs=acquad {text{and}quad r+s=-b.}
Comprobar todos los pares de enteros cuyo producto es ac da las raíces racionales, si las hay.
En resumen, si ax2+bx+c{displaystyle ax^{2}+bx+c} tiene raíces racionales hay enteros r y s tales rs=ac{displaystyle rs=ac} y r+s=− − b{displaystyle r+s=-b} (un número finito de casos para probar), y las raíces son ra{displaystyle {tfrac {} {}} {fn}}} {fn}} {fn}}} {fn}}} {fn}} y sa.{fnMicroc}. En otras palabras, uno tiene la factorización
- a()ax2+bx+c)=()ax− − r)()ax− − s).{displaystyle a(ax^{2}+bx+c)=(ax-r)(ax-s). }
Por ejemplo, consideremos el polinomio cuadrático
- 6x2+13x+6.{displaystyle 6x^{2}+13x+6.}
La inspección de los factores de ac = 36 conduce a 4 + 9 = 13 = b , dando las dos raíces
- r1=− − 46=− − 23yr2=− − 96=− − 32,{displaystyle r_{1}=-{frac {4}{6}=-{frac {2}{3}quad {text{and}}quad r_{2}=-{frac {9}{6}=-{frac {3}{2}},}
y la factorización
- 6x2+13x+6=6()x+23)()x+32)=()3x+2)()2x+3).{displaystyle 6x^{2}+13x+6=6(x+{tfrac {2}{3}})(x+{tfrac {3}{2}})=(3x+2)(2x+3). }
Usar fórmulas para raíces de polinomios
Cualquier polinomia cuadrática univariada ax2+bx+c{displaystyle ax^{2}+bx+c} se puede considerar utilizando la fórmula cuadrática:
- ax2+bx+c=a()x− − α α )()x− − β β )=a()x− − − − b+b2− − 4ac2a)()x− − − − b− − b2− − 4ac2a),{displaystyle ax^{2}+bx+c=a(x-alpha)(x-beta)=aleft(x-{frac {-b+{sqrt {b^{2}}} {2a}right)left(x-{frac}}} {-b+{sq}}}}}derecho)left(x-{frac} {-b-{sqrt {b} {2a}}}derecho),}
Donde α α {displaystyle alpha } y β β {displaystyle beta } son las dos raíces del polinomio.
Si a, b, c son todos reales, los factores son reales si y sólo si el discriminante b2− − 4ac{displaystyle b^{2}-4ac} no es negativo. De lo contrario, el polinomio cuadrático no puede ser factorizado en factores reales no constantes.
La fórmula cuadrática es válida cuando los coeficientes pertenecen a cualquier campo de característica diferente de dos y, en particular, para coeficientes en un campo finito con un número impar de elementos.
También hay fórmulas para raíces de polinomios cúbicos y cuárticos, que son, en general, demasiado complicadas para el uso práctico. El teorema de Abel-Ruffini muestra que no existen fórmulas de raíces generales en términos de radicales para polinomios de grado cinco o superior.
Uso de relaciones entre raíces
Puede ocurrir que se conozca alguna relación entre las raíces de un polinomio y sus coeficientes. Usar este conocimiento puede ayudar a factorizar el polinomio y encontrar sus raíces. La teoría de Galois se basa en un estudio sistemático de las relaciones entre raíces y coeficientes, que incluyen las fórmulas de Vieta.
Aquí, consideramos el caso más simple donde dos raíces x1{displaystyle x_{1}}y x2{displaystyle x_{2} de un polinomio P()x){displaystyle P(x)} satisfacer la relación
- x2=Q()x1),{displaystyle x_{2}=Q(x_{1}),}
donde Q es un polinomio.
Esto implica que x1{displaystyle x_{1}} es una raíz común P()Q()x)){displaystyle P(Q(x)} y P()x).{displaystyle P(x).} Por lo tanto, es una raíz del mayor divisor común de estos dos polinomios. Se deduce que este mayor divisor común es un factor no constante P()x).{displaystyle P(x).} El algoritmo euclidiano para los polinomios permite calcular este mayor factor común.
Por ejemplo, si uno sabe o adivina que: P()x)=x3− − 5x2− − 16x+80{displaystyle P(x)=x^{3}-5x^{2}-16x+80} tiene dos raíces que suma a cero, uno puede aplicar algoritmo Euclideano a P()x){displaystyle P(x)} y P()− − x).{displaystyle P(-x).} El primer paso de división consiste en añadir P()x){displaystyle P(x)} a P()− − x),{displaystyle P(-x),} dar el resto de
- − − 10()x2− − 16).{displaystyle -10(x^{2}-16).}
Entonces, dividiendo P()x){displaystyle P(x)} por x2− − 16{displaystyle x^{2}-16} da cero como un nuevo resto, y x – 5 como un cociente, que conduce a la factorización completa
- x3− − 5x2− − 16x+80=()x− − 5)()x− − 4)()x+4).{displaystyle x^{3}-5x^{2}-16x+80=(x-5)(x-4)(x+4). }
Dominios de factorización únicos
Los números enteros y los polinomios sobre un campo comparten la propiedad de factorización única, es decir, cada elemento distinto de cero se puede factorizar en un producto de un elemento invertible (una unidad, ±1 en el caso de números enteros) y un producto de elementos irreducibles (números primos, en el caso de los enteros), y esta factorización es única hasta que se reordenan los factores y se desplazan las unidades entre los factores. Los dominios integrales que comparten esta propiedad se denominan dominios de factorización única (UFD).
Los máximos comunes divisores existen en los UFD y, a la inversa, cada dominio integral en el que existen los máximos comunes divisores es un UFD. Todo dominio ideal principal es un DUF.
Un dominio euclidiano es un dominio integral sobre el que se define una división euclidiana similar a la de los números enteros. Todo dominio euclidiano es un dominio ideal principal y, por lo tanto, un DUF.
En un dominio euclidiano, la división euclidiana permite definir un algoritmo euclidiano para calcular los máximos comunes divisores. Sin embargo, esto no implica la existencia de un algoritmo de factorización. Hay un ejemplo explícito de un campo F tal que no puede existir ningún algoritmo de factorización en el dominio euclidiano F[x] de los polinomios univariados sobre F.
Ideales
En la teoría algebraica de números, el estudio de las ecuaciones diofánticas llevó a los matemáticos, durante el siglo XIX, a introducir generalizaciones de los números enteros llamados números enteros algebraicos. El primer anillo de enteros algebraicos que se han considerado fueron los enteros gaussianos y los enteros de Eisenstein, que comparten con los enteros habituales la propiedad de ser dominios ideales principales y, por lo tanto, tienen la propiedad de factorización única.
Desafortunadamente, pronto apareció que la mayoría de los anillos de los enteros algebraicos no son principales y no tienen una factorización única. El ejemplo más simple es Z[− − 5],{displaystyle mathbb {Z} [{sqrt {-5}],} en que
- 9=3⋅ ⋅ 3=()2+− − 5)()2− − − − 5),{displaystyle 9=3cdot 3=(2+{sqrt {-5})(2-{sqrt {-5}),}
y todos estos factores son irreductibles.
Esta falta de factorización única es una gran dificultad para resolver ecuaciones diofánticas. Por ejemplo, muchas demostraciones erróneas del último teorema de Fermat (probablemente incluida la "verdaderamente maravillosa demostración de Fermat, que este margen es demasiado estrecho para contener") se basaron en el supuesto implícito de factorización única.
Esta dificultad fue resuelta por Dedekind, quien demostró que los anillos de los enteros algebraicos tienen una factorización única de ideales: en estos anillos, todo ideal es un producto de ideales primos, y esta factorización es única en el orden de los factores. Los dominios integrales que tienen esta propiedad de factorización única ahora se denominan dominios de Dedekind. Tienen muchas buenas propiedades que los hacen fundamentales en la teoría algebraica de números.
Matrices
Los anillos de matriz no son conmutativos y no tienen factorización única: en general, hay muchas formas de escribir una matriz como producto de matrices. Así, el problema de factorización consiste en encontrar factores de tipos específicos. Por ejemplo, la descomposición LU da una matriz como el producto de una matriz triangular inferior por una matriz triangular superior. Como esto no siempre es posible, generalmente se considera que la "descomposición LUP" teniendo una matriz de permutación como su tercer factor.
Consulte Descomposición de matrices para conocer los tipos más comunes de factorizaciones de matrices.
Una matriz lógica representa una relación binaria y la multiplicación de matrices corresponde a la composición de relaciones. La descomposición de una relación a través de la factorización sirve para perfilar la naturaleza de la relación, como una relación difuncional.
Contenido relacionado
Listas de científicos
Operación
Compactación de ajuste de curvas
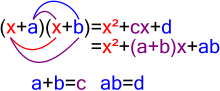





































































































































![mathbb {Z} [{sqrt {-5}}],](https://wikimedia.org/api/rest_v1/media/math/render/svg/643ef2c1e3b8b8e684a0ddf73d649cb0202cc0c1)
