Factor de empaquetamiento atómico

format_list_bulleted Contenido keyboard_arrow_down

ImprimirCitar

En cristalografía, el factor de empaquetamiento atómico (FPA), eficiencia de empaquetamiento o fracción de empaquetamiento es la fracción de volumen en una estructura cristalina que está ocupada por partículas constituyentes. Es una cantidad adimensional y siempre menor que la unidad. En los sistemas atómicos, por convención, el FPA se determina asumiendo que los átomos son esferas rígidas. El radio de las esferas se toma como el valor máximo tal que los átomos no se superponen. Para los cristales de un componente (aquellos que contienen solo un tipo de partícula), la fracción de empaquetamiento se representa matemáticamente por

{\displaystyle \mathrm {APF} ={\frac {N_{\mathrm} {particle}V_{\mathrm {particle} } {V_{\text{unit cell}}}} {\f}} {\f}}} {\f}}} {\f}}} {\f}}}}}} {\f}}}}}} {\f}}}}}}} {\

donde N_partícula es el número de partículas en la celda unitaria, V_partícula es el volumen de cada partícula y V_{celda unitaria} es el volumen ocupado por la celda unitaria. Se puede demostrar matemáticamente que para las estructuras de un solo componente, la disposición más densa de átomos tiene un FPA de aproximadamente 0,74 (véase la conjetura de Kepler), obtenido por las estructuras compactas. Para las estructuras de múltiples componentes (como las aleaciones intersticiales), el FPA puede superar 0,74.

El factor de empaquetamiento atómico de una celda unitaria es relevante para el estudio de la ciencia de los materiales, donde explica muchas propiedades de los materiales. Por ejemplo, los metales con un factor de empaquetamiento atómico alto tendrán una mayor "trabajabilidad" (maleabilidad o ductilidad), de manera similar a cómo un camino es más liso cuando las piedras están más juntas, lo que permite que los átomos de metal se deslicen entre sí con mayor facilidad.

Estructuras cristalinas de un solo componente

A continuación se enumeran los empaquetamientos esféricos comunes que adoptan los sistemas atómicos, junto con su fracción de empaquetamiento correspondiente.

Hexagonal close-packed (HCP): 0.74
cúbico centrado en la cara (FCC): 0,74 (también llamado cúbico casi lleno, CCP)
Cobijo centrado en el cuerpo (BCC): 0,68
Simple cúbico: 0,522
Diamond cubic: 0.34

La mayoría de los metales adoptan la estructura HCP, FCC o BCC.

Cúbica simple

Para un simple embalaje cúbico, el número de átomos por célula unidad es uno. El lado de la célula unidad es de longitud 2r, donde r es el radio del átomo.

{\begin{aligned}\mathrm {APF}={\frac} {N_{\mathrm {atoms} }V_{\mathrm {atom} }{V_{text{unit {\fnMicroc {1\cdot {\fnMicroc}}}}}= {\fnMicroc {1\cdot {\fnMicroc}}}}}}}}} {\fnMicroc {\fnMicroc {1\cdot {\cdot {\cdot {\fnMicroc}}}}}}}}}}}}}}}}}}}}}}}}}}} {\f}}}}} {\f}} {\f}}}} {\m}} {\m}}\fnMicrocdot {\m}}}}}} {\fn\fn\fnMicrocdot {\fnMicrocdot {\fnMicrocdot {\fn\fn\fn\fn\f}}\fnMicrocdot {\fnMicrocdot {\cdot {\f}}}}}}}}}}}}\fn {4}{3}\pi} {\fnMicrosoft Sans Serif}\[10pt] {\fnMicrosoft Sans Serif} {\fnMicroc {\pi] }\approx 0.5236\end{aligned}

Cúbica centrada en las caras

Para una celda unitaria cúbica centrada en las caras, el número de átomos es cuatro. Se puede trazar una línea desde la esquina superior de un cubo en diagonal hasta la esquina inferior del mismo lado del cubo, que es igual a 4r. Usando la geometría y la longitud del lado, a se puede relacionar con r como:

a={2r}{\sqrt {2}\,

Conociendo esto y la fórmula para el volumen de una esfera, es posible calcular el APF de la siguiente manera:

{\begin{aligned}\mathrm {APF}={\frac} {N_{\mathrm {atoms} }V_{\mathrm {atom} }{V_{text{unit {\fnMicroc {4\cdot {\fnMicroc}}}}}= {\fnMicroc {4\cdot {\fnMicroc} {4}{3}\pi} {}}}\[10pt] {\cHFF} {\cHFF} {2}}{6}\approx 0.740\,48048\end{aligned}

Cobijo centrado en el cuerpo

La célula de unidad primitiva para la estructura de cristal cúbico centrada en el cuerpo contiene varias fracciones tomadas de nueve átomos (si las partículas en el cristal son átomos): uno en cada esquina del cubo y un átomo en el centro. Debido a que el volumen de cada uno de los ocho átomos de esquina se comparte entre ocho células adyacentes, cada célula BCC contiene el volumen equivalente de dos átomos (uno central y uno en la esquina).

Cada átomo de la esquina toca al átomo del centro. Una línea que se dibuja desde una esquina del cubo a través del centro y hasta la otra esquina pasa por 4r, donde r es el radio de un átomo. Por geometría, la longitud de la diagonal es a√3. Por lo tanto, la longitud de cada lado de la estructura BCC se puede relacionar con el radio del átomo mediante

a={\frac {4r}}\,

Conociendo esto y la fórmula para el volumen de una esfera, se hace posible calcular el APF como sigue:

{\begin{aligned}\mathrm {APF}={\frac} {N_{\mathrm {atoms} }V_{\mathrm {atom} }{V_{text{unit ¿Qué? {4}{3}\pi r^{3}}{\left({\frac {4r} {\sqrt {3}}\right)}\\[10pt] {\cHFF} {\cHFF} {3}}{8}\approx 0.680\,174\,762\,\end{aligned}

Hexagonal compacto

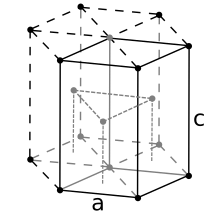
Para la estructura hexagonal envasada, la derivación es similar. Aquí la célula unidad (equivalente a 3 células de unidad primitivas) es un prisma hexagonal que contiene seis átomos (si las partículas en el cristal son átomos). De hecho, tres son los átomos en la capa media (dentro del prisma); además, para las capas superior e inferior (en las bases del prisma), el átomo central se comparte con la célula adyacente, y cada uno de los seis átomos en los vértices se comparte con otras seis células adyacentes. Así que el número total de átomos en la celda es de 3 + (1/2)×2 + (1/6)×6×2 = 6. Cada átomo toca otros doce átomos. Ahora $a$ ser la longitud lateral de la base del prisma y $c$ sea su altura. Este último es dos veces la distancia entre capas adyacentes, i. e., dos veces la altura del tetraedro regular cuyos vértices están ocupados por (por ejemplo) el átomo central de la capa inferior, dos átomos no centrales adyacentes de la misma capa, y un átomo de la capa media "resting" en los tres anteriores. Obviamente, el borde de este tetraedro es $a$ . Si $a=2r$ , entonces su altura se puede calcular fácilmente ${\fnMicroc} {8}{3}a}a}$ , y, por consiguiente, $c=4{\sqrt {\tfrac {2} {3}}r\$ . Así que el volumen de la célula hcp unidad resulta ser (3/2)√3 $a^{2}c$ que es 24√2 $r^{3}$ .

Entonces es posible calcular el APF como sigue:

{\begin{aligned}\mathrm {APF}={\frac} {N_{\mathrm {atoms} }V_{\mathrm {atom} }{V_{text{unit ♪♪♪♪♪♪♪ {6\cdot {\fnMicroc} {4}{3}\pi r^{3}{{{{\frac} {\f} {\f} {\f} {\f}} {\f} {\fn}}}}}} {\f} {\fn}}}}}}}}\p}}\p}\p}\f}\f}\f}\f}\f}}\f}\f}\f}\f}\f}}\f}\f}\f}\f}\f}\f}\f}\f}\f}\f}\f}\f}\f}\f}\f}\f}\f}\f}\f}\f}\f}\f}\f}\f}\f}\f}\f}\f}\f}\f}\f}\f}\f}\f}\f}\f}\f}\f}\f}\f}\f}\f}\f}\f}\f}\f}}\f}\f}\ {3{\sqrt {3}} {2}a}{2}c}\\\[10pt] Conden={\frac {6\cdot {\frac] {4}{3}\pi r^{3}{{{{\frac} {\f} {\f} {\f} {\f}} {\f} {\fn}}}}}} {\f} {\fn}}}}}}}}\p}}\p}\p}\f}\f}\f}\f}\f}}\f}\f}\f}\f}\f}}\f}\f}\f}\f}\f}\f}\f}\f}\f}\f}\f}\f}\f}\f}\f}\f}\f}\f}\f}\f}\f}\f}\f}\f}\f}\f}\f}\f}\f}\f}\f}\f}\f}\f}\f}\f}\f}\f}\f}\f}\f}\f}\f}\f}\f}\f}}\f}\f}\ {3{\sqrt {3}} {2r)}{2}{2}{\sqrt {\frac} {\fnMic}} {\fnK}} {\fnK}} {\fnK}} {\fnK} {\f}}}} {\fnK}}} {\fnK\f}}}}} {\f}}}}}} {\f}}}}}}}}}}}}}}}}}}}} {\c}}}}} {\f}}}}} {\f}}}} {\f}}}}}}}}}}}}}}}}} {\c}}}}} {\c} {\c} {\c}}}}} {\c} {\c}} {\c\c\c\c\c\c} {\c}}}}}}} {\c\c\c\c\c\c\c}}}}}}}}} {\c}}} {2}{3}}\cdot 4r}={\frac {6\cdot {\frac}} {\cdot} {\cdot}} {\cdot {6\cdot {\cdot {\cdot}}} {\cdot 4r}}} {\cdot}}} {\cdot {\cdot}}}}} {\cdot {\cdot {\cdot {\cdot {\cdot {\cdot}}}} {\cdot {\cdot {\cdot {\cdot {\cdot {\c}}}}}}}}}}}}}}} {\cdot {\cdot {\cdot {\cdot {\cdot {\cdot {\cdot {\cdot {\cdot {\cdot {\cdot {\c} {\c}}}}}}}}}}}}}}}} {4}{3}\pi r^{3}{{{{\frac} {\f} {\f} {\f} {\f}} {\f} {\fn}}}}}} {\f} {\fn}}}}}}}}\p}}\p}\p}\f}\f}\f}\f}\f}}\f}\f}\f}\f}\f}}\f}\f}\f}\f}\f}\f}\f}\f}\f}\f}\f}\f}\f}\f}\f}\f}\f}\f}\f}\f}\f}\f}\f}\f}\f}\f}\f}\f}\f}\f}\f}\f}\f}\f}\f}\f}\f}\f}\f}\f}\f}\f}\f}\f}\f}\f}}\f}\f}\ {3{\sqrt {3}}{2} {\sqrt {2}}\cdot 16r^{3}}\\[10pt] } {\sqrt {18}}={\frac {\pi}{3{\sqrt {2}}\approx 0.740\,480\,48\,\end{aligned}}

Más resultados...