Factor de compresibilidad
En la termodinámica, factor de compresión ()Z), también conocido como el factor de compresión o el Factor de desviación de gas, describe la desviación de un gas real de comportamiento gas ideal. Se define simplemente como la relación del volumen molar de un gas al volumen molar de un gas ideal a la misma temperatura y presión. Es una propiedad termodinámica útil para modificar la ley de gas ideal para explicar el comportamiento real del gas. En general, la desviación del comportamiento ideal se hace más significativa cuanto más cerca un gas es a un cambio de fase, menor la temperatura o mayor la presión. Los valores de factor de compresión se obtienen generalmente por cálculo de ecuaciones de estado (EOS), como la ecuación virial que toma constantes empíricas específicas para compuestos como entrada. Para un gas que es una mezcla de dos o más gases puros (aire o gas natural, por ejemplo), la composición del gas debe ser conocida antes de que se pueda calcular la compresión.
Alternativamente, el factor de compresibilidad para gases específicos se puede leer a partir de gráficos de compresión generalizados que trazan Z{displaystyle Z} como función de presión a temperatura constante.
El factor de compresibilidad no debe confundirse con la compresibilidad (también conocida como coeficiente de compresibilidad o compresibilidad isotérmica) de un material, que es la medida del cambio de volumen relativo de un fluido o sólido en respuesta a un cambio de presión.
Definición y significado físico

El factor de compresibilidad se define frecuentemente en termodinámica e ingeniería como:
- Z=p*** *** RespecíficoT,{displaystyle Z={frac {p}{rho ¿Qué?
donde p es la presión, *** *** {displaystyle rho } es la densidad del gas y Respecífico=RM{fnMicrosoftstyle R_{text{specific}={frac {R} {M}} es la constante de gas específica, M{displaystyle M} ser la masa molar, y la T{displaystyle T} es la temperatura absoluta (escala de Kelvin o Rankine).
En mecánica estadística la descripción es:
- Z=pVnRT{displaystyle Z={frac {pV} {nRT}}
donde p es la presión, n es el número de lunares de gas, T{displaystyle T} es la temperatura absoluta, R{displaystyle R. es la constante de gas, V es unidad Volumen
Para un gas ideal el factor de compresión es Z=1{displaystyle Z=1} por definición. En muchas aplicaciones mundiales reales los requisitos de precisión exigen que se tengan en cuenta las desviaciones del comportamiento ideal del gas, es decir, el comportamiento real del gas. El valor de Z{displaystyle Z} generalmente aumenta con presión y disminuye con temperatura. A altas presiones las moléculas están colisionando más a menudo. Esto permite que las fuerzas repulsivas entre moléculas tengan un efecto notable, haciendo el volumen molar del gas real (Vm{displaystyle V_{mathrm}}) mayor que el volumen molar del gas ideal correspondiente (()Vm)gas ideal=RT/p{displaystyle (V_{mathrm})_{text{ideal G.), que causa Z{displaystyle Z} para superar uno. Cuando las presiones son más bajas, las moléculas son libres de moverse. En este caso dominan fuerzas atractivas, haciendo <math alttext="{displaystyle ZZc)1{displaystyle Z won1}<img alt="{displaystyle Z. Cuanto más cerca esté el gas a su punto crítico o su punto de ebullición, más Z{displaystyle Z} se desvía del caso ideal.
Fugacidad
El factor de compresibilidad está vinculado a la fugacidad por la relación:
- f=Pexp ()∫ ∫ Z− − 1PdP){displaystyle f=Pexp left(int {frac {Z-1} {P}dPright)}
Gráficos de factor de compresión generalizados para gases puros

La relación única entre el factor de compresión y la temperatura reducida, Tr{displaystyle T_{r}, y la presión reducida, Pr{displaystyle P_{r}, fue reconocido por primera vez por Johannes Diderik van der Waals en 1873 y es conocido como el principio de dos parámetros de los estados correspondientes. El principio de los estados correspondientes expresa la generalización de que las propiedades de un gas que dependen de las fuerzas intermoleculares están relacionadas con las propiedades críticas del gas de una manera universal. Esto proporciona una base más importante para desarrollar correlaciones de propiedades moleculares.
En cuanto a la compresión de los gases, el principio de los estados correspondientes indica que cualquier gas puro a la misma temperatura reducida, Tr{displaystyle T_{r}, y reducción de la presión, Pr{displaystyle P_{r}, debe tener el mismo factor de compresión.
La temperatura y presión reducidas están definidas por
- Tr=TTc{displaystyle T_{r}={frac {T} {T_{c}}} y Pr=PPc.{displaystyle P_{r}={frac {P} {P_{c}}}}
Aquí. Tc{displaystyle T_{c} y Pc{displaystyle P_{c} son conocidos como la temperatura crítica y la presión crítica de un gas. Son características de cada gas específico con Tc{displaystyle T_{c} ser la temperatura por encima de la cual no es posible licuar un gas dado y Pc{displaystyle P_{c} es la presión mínima necesaria para licuar un gas dado a su temperatura crítica. Juntos definen el punto crítico de un líquido sobre el cual no existen fases distintas de líquido y gas de un líquido dado.
Los datos de presión-volumen-temperatura (PVT) de los gases reales varían de un gas puro a otro. Sin embargo, cuando se grafican los factores de compresibilidad de varios gases de un solo componente versus la presión junto con las isotermas de temperatura, muchos de los gráficos exhiben formas de isoterma similares.
Para obtener un gráfico generalizado que se puede utilizar para muchos gases diferentes, la presión y la temperatura reducidas, Pr{displaystyle P_{r} y Tr{displaystyle T_{r}, se utilizan para normalizar los datos del factor de compresión. La Figura 2 es un ejemplo de un gráfico de factor de compresión generalizado derivado de cientos de puntos de datos experimentales PVT de 10 gases puros, a saber, metano, etano, etileno, propano, n-butano, i-pentano, n-hexano, nitrógeno, dióxido de carbono y vapor.
Hay gráficos de factor de compresión generalizados más detallados basados en hasta 25 o más gases puros diferentes, como los gráficos Nelson-Obert. Se dice que estos gráficos tienen una precisión dentro del 1–2 por ciento para Z{displaystyle Z} valores superiores a 0,6 y dentro de 4–6 por ciento para Z{displaystyle Z} valores de 0,3 a 0,6.
Los gráficos del factor de compresión generalizado pueden ser considerablemente erróneos por gases fuertemente polares que son gases para los cuales los centros de carga positiva y negativa no coinciden. En tales casos la estimación Z{displaystyle Z} puede estar en error hasta entre 15 y 20 por ciento.
Los gases cuánticos hidrógeno, helio y neón no se ajustan al comportamiento de los estados correspondientes y la presión y temperatura reducidas para esos tres gases deben redefinirse de la siguiente manera para mejorar la precisión de la predicción de sus factores de compresibilidad cuando se utiliza el gráficos generalizados:
- Tr=TTc+8{displaystyle T_{r}={frac {T} {T_{c}+8}}} y Pr=PPc+8{displaystyle P_{r}={frac {P_{c}+8}}
donde las temperaturas están en kelvins y las presiones en atmósferas.
Lectura de una tabla de compresibilidad generalizada
Para leer una tabla de compresibilidad, se deben conocer la presión reducida y la temperatura. Si se desconoce la presión o la temperatura reducida, se debe encontrar el volumen específico reducido. A diferencia de la presión y temperatura reducidas, el volumen específico reducido no se encuentra utilizando el volumen crítico. El volumen específico reducido se define por,
- . . R=. . efectivosRTcr/Pcr{displaystyle nu _{R}={frac {nu {fnK} {fnK} {fnK}} {fnMicrosoft}}}}
Donde . . efectivos{displaystyle nu _{actual}} es el volumen específico.
Una vez encontradas dos de las tres propiedades reducidas, se puede utilizar la tabla de compresibilidad. En una tabla de compresibilidad, la presión reducida está en el eje x y Z está en el eje y. Cuando se le dan la presión y la temperatura reducidas, encuentre la presión dada en el eje x. A partir de ahí, avance en el gráfico hasta encontrar la temperatura reducida dada. Z se encuentra mirando donde se cruzan esos dos puntos. Se puede seguir el mismo proceso si se proporciona un volumen específico reducido con presión o temperatura reducidas.
Observaciones realizadas a partir de una tabla de compresibilidad generalizada
Hay tres observaciones que se pueden hacer al observar un gráfico de compresibilidad generalizada. Estas observaciones son:
- Los gases se comportan como un gas ideal independientemente de la temperatura cuando la presión reducida es mucho menos que uno (PR ≪ 1).
- Cuando la temperatura reducida es mayor que dos (T)R Ø 2), comportamiento ideal-gas se puede asumir independientemente de la presión, a menos que la presión sea mucho mayor que una (PR ≫ 1).
- Los gases se desvían del comportamiento ideal-gas más cerca del punto crítico.
Modelos teóricos
La ecuación virial es especialmente útil para describir las causas de la no idealidad a nivel molecular (muy pocos gases son monoatómicos), ya que se deriva directamente de la mecánica estadística:
- Z=1+BVm+CVm2+DVm3+... ... {displaystyle Z=1+{frac {B}{V_{mathrm} {fnK}}+ {fnMicroc}{V_{mathrm {m} {m}} {fnMicroc} {D}{V_{mathrm} {m} {m}} {m} {m}} {m}} {m}} {m}} {m} {m} {m} {m} {m} {m}} {m} {m}}} {m} {m} {m} {m} {m} {m} {m}}}} {}}}}}}}}}}}} {}} {}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}} { dot}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}} { dot}} { dot}} { dot} { dots}
Donde los coeficientes en el numerador son conocidos como coeficientes viales y son funciones de temperatura.
Los coeficientes virials representan interacciones entre grupos sucesivos más grandes de moléculas. Por ejemplo, B{displaystyle B} cuentas para interacciones entre pares, C{displaystyle C} para interacciones entre tres moléculas de gas, etc. Debido a que las interacciones entre grandes cantidades de moléculas son raras, la ecuación virial es generalmente truncada después del tercer término.
Cuando se supone este truncamiento, el factor de compresibilidad está vinculado al potencial de fuerza intermolecular φ mediante:
- Z=1+2π π NAVm∫ ∫ 0JUEGO JUEGO ()1− − exp ()φ φ kT))r2dr{displaystyle Z=1+2pi {fnMicroc {N_{text{A} {fn} {fnK}} {f}} {f}} {f}} {f}}} {fn}}} {f}}} {fn}}}}}} {f}}}} {f}}} {f}}}} {f}}}}}}}}}}}}}}}}}}}} { ¿Por qué? Bien.
El artículo del gas real cuenta con métodos más teóricos para calcular los factores de compresión.
Mecanismo físico de dependencia de la temperatura y la presión
Las desviaciones del factor de compresibilidad, Z, respecto de la unidad se deben a fuerzas intermoleculares de atracción y repulsión. A una temperatura y presión dadas, las fuerzas repulsivas tienden a hacer que el volumen sea mayor que el de un gas ideal; cuando estas fuerzas dominan Z es mayor que la unidad. Cuando dominan las fuerzas de atracción, Z es menor que la unidad. La importancia relativa de las fuerzas de atracción disminuye a medida que aumenta la temperatura (ver efecto sobre los gases).
Como se vio arriba, el comportamiento de Z es cualitativamente similar para todos los gases. El nitrógeno molecular, N2, se utiliza aquí para describir y comprender mejor ese comportamiento. Todos los datos utilizados en esta sección se obtuvieron del NIST Chemistry WebBook. Es útil observar que para N2 el punto de ebullición normal del líquido es 77,4 K y el punto crítico está en 126,2 K y 34,0 bar.

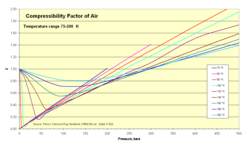
La figura de la derecha muestra una descripción general que cubre un amplio rango de temperaturas. A baja temperatura (100 K), la curva tiene una forma característica de marca de verificación; la parte ascendente de la curva es casi directamente proporcional a la presión. A temperatura intermedia (160 K), hay una curva suave con un mínimo amplio; aunque la porción de alta presión vuelve a ser casi lineal, ya no es directamente proporcional a la presión. Finalmente, a alta temperatura (400 K), Z está por encima de la unidad en todas las presiones. Para todas las curvas, Z se aproxima al valor de unidad del gas ideal a baja presión y excede ese valor a muy alta presión.

Para comprender mejor estas curvas, en la segunda figura se ofrece una mirada más cercana al comportamiento a baja temperatura y presión. Todas las curvas comienzan con Z igual a la unidad a presión cero y Z inicialmente disminuye a medida que aumenta la presión. El N2 es un gas en estas condiciones, por lo que la distancia entre las moléculas es grande, pero se vuelve más pequeña a medida que aumenta la presión. Esto aumenta las interacciones atractivas entre moléculas, acercando las moléculas y haciendo que el volumen sea menor que el de un gas ideal a la misma temperatura y presión. Una temperatura más alta reduce el efecto de las interacciones atractivas y el gas se comporta de una manera casi ideal.
A medida que aumenta la presión, el gas finalmente alcanza la curva de coexistencia gas-líquido, que se muestra con la línea discontinua en la figura. Cuando eso sucede, las interacciones atractivas se vuelven lo suficientemente fuertes como para superar la tendencia del movimiento térmico a hacer que las moléculas se expandan; entonces el gas se condensa para formar un líquido. Los puntos en las porciones verticales de las curvas corresponden a que N2 es en parte gas y en parte líquido. En la curva de coexistencia, existen entonces dos valores posibles para Z, uno mayor correspondiente al gas y un valor menor correspondiente al líquido. Una vez que todo el gas se ha convertido en líquido, el volumen disminuye sólo ligeramente con nuevos aumentos de presión; entonces Z es casi proporcional a la presión.
A medida que la temperatura y la presión aumentan a lo largo de la curva de coexistencia, el gas se parece más a un líquido y el líquido se parece más a un gas. En el punto crítico, los dos son iguales. Entonces, para temperaturas superiores a la temperatura crítica (126,2 K), no hay transición de fase; A medida que aumenta la presión, el gas se transforma gradualmente en algo más parecido a un líquido. Justo encima del punto crítico hay un rango de presión para el cual Z cae bastante rápidamente (ver la curva de 130 K), pero a temperaturas más altas el proceso es completamente gradual.

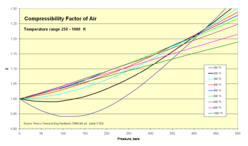
Las cifras finales muestran el comportamiento a temperaturas muy por encima de las temperaturas críticas. Las interacciones repulsivas esencialmente no se ven afectadas por la temperatura, pero las interacciones atractivas tienen cada vez menos influencia. Por tanto, a una temperatura suficientemente alta, las interacciones repulsivas dominan en todas las presiones.
Esto se puede ver en el gráfico que muestra el comportamiento a alta temperatura. A medida que aumenta la temperatura, la pendiente inicial se vuelve menos negativa, la presión a la que Z es mínima se reduce y la presión a la que las interacciones repulsivas comienzan a dominar, es decir, donde Z va de menor que la unidad a mayor que la unidad, se hace más pequeño. A la temperatura de Boyle (327 K para N2), los efectos de atracción y repulsión se cancelan entre sí a baja presión. Entonces Z permanece en el valor del gas ideal de la unidad hasta presiones de varias decenas de bar. Por encima de la temperatura de Boyle, el factor de compresibilidad es siempre mayor que la unidad y aumenta lenta pero constantemente a medida que aumenta la presión.
Valores experimentales
Es extremadamente difícil generalizar a qué presiones o temperaturas se vuelve importante la desviación del gas ideal. Como regla de pulgar, la ley de gas ideal es razonablemente precisa hasta una presión de aproximadamente 2 am, e incluso superior para pequeñas moléculas no asociativas. Por ejemplo, el metilcloruro, una molécula altamente polar y, por lo tanto, con fuerzas intermoleculares significativas, el valor experimental del factor de compresión es Z=0.9152{displaystyle Z=0.9152} a una presión de 10 am y temperatura de 100 °C. Para el aire (pequeñas moléculas no polares) en aproximadamente las mismas condiciones, el factor de compresión es sólo Z=1.0025{displaystyle Z=1.0025} (ver tabla abajo para 10 bares, 400 K).
Compresibilidad del aire
El aire normal contiene en cantidades brutas un 80 por ciento de nitrógeno N
2 y 20 por ciento de oxígeno O
2. Ambas moléculas son pequeñas y no polares (y por tanto no asociativas). Por lo tanto, podemos esperar que el comportamiento del aire dentro de amplios rangos de temperatura y presión pueda aproximarse al de un gas ideal con una precisión razonable. Los valores experimentales del factor de compresibilidad lo confirman.
- Z para aire como función de presión 1–500 bar
- 75–200 K isotherms
- 250–1000 K isotherms
| Temperatura. (K) | Presión, absoluta (bar) | |||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 5 | 10 | 20 | 40 | 60 | 80 | 100 | 150 | 200 | 250 | 300 | 400 | 500 | |
| 75 | 0,0052 | 0,0260 | 0,0519 | 0.1036 | 0.2063 | 0.3082 | 0.4094 | 0,5099 | 0,581 | 1.0125 | ||||
| 80 | 0.0250 | 0,0499 | 0,0995 | 0.1981 | 0,2958 | 0,3927 | 0.4887 | 0,7258 | 0,9588 | 1.1931 | 1.4139 | |||
| 90 | 0.9764 | 0,0236 | 0,0453 | 0,0940 | 0.1866 | 0,2781 | 0,3686 | 0.4681 | 0.6779 | 0.8929 | 1.1098 | 1.3110 | 1.7161 | 2.1105 |
| 100 | 0.9797 | 0.8872 | 0,0453 | 0,0900 | 0.1782 | 0,2635 | 0,3498 | 0.4337 | 0,6386 | 0.8377 | 1.0395 | 1.2227 | 1.5937 | 1.9536 |
| 120 | 0,9880 | 0,973 | 0.8860 | 0,6730 | 0.1778 | 0,2557 | 0,371 | 0.4132 | 0,564 | 0,7720 | 0,9530 | 1.1076 | 1.5091 | 1.7366 |
| 140 | 0.9927 | 0.9614 | 0,9205 | 0,8297 | 0,5856 | 0,3313 | 0.3737 | 0.4340 | 0,599 | 0,7699 | 0.9114 | 1.0393 | 1.3202 | 1.5903 |
| 160 | 0.9951 | 0.9748 | 0.9489 | 0.8954 | 0,803 | 0,603 | 0,5696 | 0,489 | 0,6340 | 0,764 | 0.8840 | 1.0105 | 1.2585 | 1.4970 |
| 180 | 0.9967 | 0.9832 | 0,9660 | 0,9314 | 0.8625 | 0,7977 | 0,732 | 0,784 | 0.7180 | 0,786 | 0,900 | 1.0068 | 1.2232 | 1.4361 |
| 200 | 0.9978 | 0.9886 | 0,9767 | 0.9539 | 0.9100 | 0.8701 | 0.8374 | 0.8142 | 0.8061 | 0.8549 | 0,9311 | 1.0185 | 1.2054 | 1.3944 |
| 250 | 0.9992 | 0,957 | 0.9911 | 0,822 | 0.9671 | 0.9549 | 0.9463 | 0.9411 | 0.9450 | 0.9713 | 1.0152 | 1.0702 | 1.1990 | 1.3392 |
| 300 | 0.9999 | 0.9987 | 0.9974 | 0.9950 | 0.9917 | 0.9901 | 0,903 | 0.9930 | 1.0074 | 1.0326 | 1.0669 | 1.1089 | 1.2073 | 1.3163 |
| 350 | 1.0000 | 1.0002 | 1.0004 | 1.0014 | 1.0038 | 1.0075 | 1.0121 | 1.0183 | 1.0377 | 1.0635 | 1.0947 | 1.1303 | 1.2116 | 1.3015 |
| 400 | 1.0002 | 1.0012 | 1.0025 | 1.0046 | 1.0100 | 1.0159 | 1.0229 | 1.0312 | 1.0533 | 1.0795 | 1.1087 | 1.1411 | 1.2117 | 1.2890 |
| 450 | 1.0003 | 1.0016 | 1.0034 | 1.0063 | 1.0133 | 1.0210 | 1.0287 | 1.0374 | 1.0614 | 1.0913 | 1.1183 | 1.1463 | 1.2090 | 1.2778 |
| 500 | 1.0003 | 1.0020 | 1.0034 | 1.0074 | 1.0151 | 1.0234 | 1.0323 | 1.0410 | 1.0650 | 1.0913 | 1.1183 | 1.1463 | 1.2051 | 1.2667 |
| 600 | 1.0004 | 1.0022 | 1.0039 | 1.0081 | 1.0164 | 1.0253 | 1.0340 | 1.0434 | 1.0678 | 1.0920 | 1.1172 | 1.1427 | 1.1947 | 1.2475 |
| 800 | 1.0004 | 1.0020 | 1.0038 | 1.0077 | 1.0157 | 1.0240 | 1.0321 | 1.0408 | 1.0621 | 1.0844 | 1.1061 | 1.1283 | 1.1720 | 1.2150 |
| 1000 | 1.0004 | 1.0018 | 1.0037 | 1.0068 | 1.0142 | 1.0215 | 1.0290 | 1.0365 | 1.0556 | 1.0744 | 1.0948 | 1.1131 | 1.1515 | 1.1889 |
Z{displaystyle Z} Los valores se calculan a partir de valores de presión, volumen (o densidad), y temperatura en Vasserman, Kazavchinskii y Rabinovich, "Thermophysical Properties of Air and Air Components; ' Moscow, Nauka, 1966, y NBS-NSF Trans. TT 70-50095, 1971: y Vasserman y Rabinovich, "Thermophysical Properties of Liquid Air and Its Component, "Moscow, 1968, y NBS-NSF Trans. 69-55092, 1970.
Contenido relacionado
Julio (unidad)
Ley de Fick
Pascal (unidad)