Exponenciación
Exponenciación es una operación matemática, escrita como bn, que involucra dos números, la base b y el exponente o poder n, y se pronuncia como "b (elevado) a la (potencia de) n& #34;. Cuando n es un entero positivo, la exponenciación corresponde a la multiplicación repetida de la base: es decir, bn es el producto de multiplicar n bases:
El exponente generalmente se muestra como un superíndice a la derecha de la base. En ese caso, bn se llama "b elevado a la nésima potencia", "b (elevado) a la potencia de n", "la nésima potencia de b", "b a la nésima potencia", o más brevemente como "b a la nésima".
Partiendo del hecho básico indicado anteriormente que, para cualquier entero positivo n{displaystyle n}, bn{displaystyle b^{n} es n{displaystyle n} sucesos de b{displaystyle b} todo multiplicado por el otro, varias otras propiedades de exponenciación siguen directamente. En particular:
En otras palabras, al multiplicar una base elevada a un exponente por la misma base elevada a otro exponente, los exponentes agregan. De esta regla básica que los exponentes añaden, podemos derivar que b0{displaystyle b^{0} debe ser igual a 1, como sigue. Para cualquier n{displaystyle n}, b0⋅ ⋅ bn=b0+n=bn{displaystyle b^{0}cdot ¿Qué?. Dividir ambos lados por bn{displaystyle b^{n} da b0=bn/bn=1{displaystyle - Sí..
El hecho de que b1=b{displaystyle B^{1}=b} puede derivarse de la misma regla. Por ejemplo, ()b1)3=b1⋅ ⋅ b1⋅ ⋅ b1=b1+1+1=b3{displaystyle (b^{1}=b^{1}cdot b^{1}cdot b^{1}=b^{1+1+1}=b^{3}. Tomando la raíz del cubo de ambos lados da b1=b{displaystyle B^{1}=b}.
La regla que multiplica los exponentes añade también se puede utilizar para derivar las propiedades de los exponentes enteros negativos. Considerar la cuestión de qué b− − 1{displaystyle b^{-1} Debería significar. Para respetar la regla "exponentes agregan", debe ser el caso que b− − 1⋅ ⋅ b1=b− − 1+1=b0=1{displaystyle b^{-1}cdot b^{1}=b^{-1+1}=b^{0}=1}. Dividir ambos lados por b1{displaystyle b^{1} da b− − 1=1/b1{displaystyle b^{-1}=1/b^{1}, que puede ser más simplemente escrito como b− − 1=1/b{displaystyle b^{-1}=1/b}, utilizando el resultado de arriba que b1=b{displaystyle B^{1}=b}. Por un argumento similar, b− − n=1/bn{displaystyle B^{-n}=1/b^{n}.
Las propiedades de los exponentes fraccionales también siguen de la misma regla. Por ejemplo, supongamos que consideramos b{displaystyle {sqrt {b}} y preguntar si hay algún exponente adecuado, que podemos llamar r{displaystyle r}, tal que br=b{displaystyle b^{r}={sqrt {b}}. De la definición de la raíz cuadrada, tenemos que b⋅ ⋅ b=b{displaystyle {sqrt {b}cdot {sqrt {b}=b}. Por lo tanto, el exponente r{displaystyle r} debe ser tal br⋅ ⋅ br=b{displaystyle b^{r}cdot B^{r}=b}. Usando el hecho de que multiplicar hace que los exponentes añadir br+r=b{displaystyle b^{r+r}=b}. El b{displaystyle b} en el lado derecho también se puede escribir como b1{displaystyle b^{1}, dar br+r=b1{displaystyle b^{r+r}=b^{1}. equiparando a los exponentes en ambos lados, tenemos r+r=1{displaystyle r+r=1}. Por lo tanto, r=12{displaystyle r={frac {1}{2}}}Así que b=b1/2{displaystyle {sqrt {b}=b^{1/2}.
La definición de exponenciación se puede ampliar para permitir cualquier exponente real o complejo. La potenciación por exponentes enteros también se puede definir para una amplia variedad de estructuras algebraicas, incluidas las matrices.
La potenciación se utiliza ampliamente en muchos campos, incluidos la economía, la biología, la química, la física y la informática, con aplicaciones como el interés compuesto, el crecimiento de la población, la cinética de las reacciones químicas, el comportamiento de las ondas y la criptografía de clave pública.
Historia de la notación
El término poder (latín: potentia, potestas, dignitas) es una mala traducción del griego antiguo δύναμις (dúnamis, aquí: "amplificación") utilizado por el matemático griego Euclides para el cuadrado de una línea, siguiendo a Hipócrates de Quíos. En The Sand Reckoner, Arquímedes descubrió y probó la ley de los exponentes, 10a · 10 b = 10a+b, necesario para manipular poderes de 10. En el siglo IX, el matemático persa Muhammad ibn Mūsā al-Khwārizmī usó los términos مَال (māl, "posesiones", "propiedad") para un cuadrado: los musulmanes, "como la mayoría de los matemáticos de aquellos tiempos y anteriores, pensaban en un número cuadrado como una representación de un área, especialmente de la tierra, por lo tanto propiedad"—y كَعْبَة (kaʿbah, "cubo") por un cubo, que los matemáticos islámicos posteriores representaron en notación matemática como las letras mīm (m) y kāf (k), respectivamente, por el siglo XV, como se ve en el trabajo de Abū al-Hasan ibn Alī al-Qalasādī.
A finales del siglo XVI, Jost Bürgi utilizó números romanos para los exponentes.
Nicolas Chuquet utilizó una forma de notación exponencial en el siglo XV, que luego fue utilizada por Henricus Grammateus y Michael Stifel en el siglo XVI. La palabra exponente fue acuñada en 1544 por Michael Stifel. Samuel Jeake introdujo el término índices en 1696. En el siglo XVI, Robert Recorde utilizó los términos cuadrado, cubo, zenzizenzic (cuarta potencia), sursolid (quinta), zenzicube (sexta), segunda sursolid (séptima), y zenzizenzinzic (octavo). Biquadrate también se ha utilizado para referirse a la cuarta potencia.
A principios del siglo XVII, René Descartes introdujo la primera forma de nuestra notación exponencial moderna en su texto titulado La Géométrie; allí, la notación se introduce en el Libro I.
Algunos matemáticos (como René Descartes) usaron exponentes solo para potencias mayores a dos, prefiriendo representar cuadrados como multiplicaciones repetidas. Así escribirían polinomios, por ejemplo, como ax + bxx + cx3 + d.
Otro sinónimo histórico, involución, ahora es raro y no debe confundirse con su significado más común.
En 1748, Leonhard Euler introdujo exponentes variables e, implícitamente, exponentes no enteros al escribir:
"considerar exponenciales o poderes en los que el propio exponente es una variable. Está claro que las cantidades de este tipo no son funciones algebraicas, ya que en esos los exponentes deben ser constantes."
Terminología
La expresión b2 = b · b se llama "el cuadrado de b" o "b al cuadrado", porque el área de un cuadrado con lado de longitud b es b2.
Del mismo modo, la expresión b3 = b · b · b se llama "el cubo de b" o "b al cubo", porque el volumen de un cubo con lado de longitud b es b3.
Cuando es un número entero positivo, el exponente indica cuántas copias de la base se multiplican. Por ejemplo, 35 = 3 · 3 · 3 · 3 · 3 = 243. La base 3 aparece 5 veces en la multiplicación, porque el exponente es 5. Aquí, 243 es la quinta potencia de 3, o 3 elevado a la quinta potencia.
La palabra "criado" generalmente se omite y, a veces, "power" también, por lo que 35 puede leerse simplemente "3 a la 5ª", o "3 a la 5& #34;. Por lo tanto, la exponenciación bn se puede expresar como " b a la potencia de n", "b a la nésima potencia", "b a la nésima", o más brevemente como "b a la n".
Una fórmula con exponenciación anidada, como 357 (que significa) 3(57) y no (3)5)7), se llama una torre de poderes, o simplemente una torre. Por ejemplo escribiendo bcd{displaystyle b^{c^{d}} es equivalente a la escritura b()cd){displaystyle b^{left(c^{d}right)}. Esto se puede generalizar a donde se escribe bcdf{displaystyle b^{c^{d^{f}}} medios b()c()df)){displaystyle b^{left(c^{left(d^{f}right)}}}. Por ejemplo, 100{displaystyle {sqrt {100}} puede ser calculado como 10012{displaystyle 100^{frac {1}{2}}}, que puede ser calculado como 1002− − 1{displaystyle 100., que es igual a 100()2− − 1){displaystyle 100^{left(2^{-1}right)}, que es igual a 10.
Exponentes enteros
La operación de exponenciación con exponentes enteros se puede definir directamente a partir de operaciones aritméticas elementales.
Exponentes positivos
La definición de la exponenciación como una multiplicación iterada se puede formalizar usando la inducción, y esta definición se puede usar tan pronto como se tenga una multiplicación asociativa:
El caso base es
- b1=b{displaystyle B^{1}=b}
y la recurrencia es
- bn+1=bn⋅ ⋅ b.{displaystyle b^{n+1}=b^{n}cdot b.}
La asociatividad de la multiplicación implica que para cualquier entero positivo m y n,
- bm+n=bm⋅ ⋅ bn,{displaystyle b^{m+n}=b^{m}cdot b^{n}
y
- ()bm)n=bmn.{displaystyle (b^{m}=b^{mn}
Exponente cero
Por definición, cualquier número distinto de cero elevado a la potencia 0 es 1:
- b0=1.{displaystyle b^{0}=1.}
Esta definición es la única posible que permite extender la fórmula
- bm+n=bm⋅ ⋅ bn{displaystyle b^{m+n}=b^{m}cdot B^{n}
a cero exponentes. Se puede usar en toda estructura algebraica con una multiplicación que tenga identidad.
Intuitivamente, b0{displaystyle b^{0} puede interpretarse como el producto vacío de copias b. Entonces, la igualdad b0=1{displaystyle B^{0}=1} es un caso especial de la convención general para el producto vacío.
El caso 00 es más complicado. En contextos donde sólo se consideran poderes enteros, el valor 1 se asigna generalmente a 00,{displaystyle 0^{0} pero, de lo contrario, la elección de si asignarle un valor y qué valor asignar puede depender del contexto.
Exponentes negativos
La potenciación con exponentes negativos se define por la siguiente identidad, que se cumple para cualquier número entero n y distinto de cero b:
- b− − n=1bn{displaystyle b^{-n}={frac} {1}{b^ {n}}}}.
El aumento de 0 a un exponente negativo es indefinido pero, en algunas circunstancias, puede ser interpretado como infinidad (infinito)JUEGO JUEGO {displaystyle infty }).
Esta definición de exponenciación con exponentes negativos es la única que permite ampliar la identidad bm+n=bm⋅ ⋅ bn{displaystyle b^{m+n}=b^{m}cdot B^{n} a los exponentes negativos (considerar el caso m=− − n{displaystyle m=-n}).
La misma definición se aplica a los elementos invertibles en un monoide multiplicativo, es decir, una estructura algebraica, con una multiplicación asociativa y una identidad multiplicativa denotada 1 (por ejemplo, las matrices cuadradas de una dimensión determinada). En particular, en tal estructura, el inverso de un elemento invertible x está denotado x− − 1.{displaystyle x^{-1}
Identidades y propiedades
Las siguientes identidades, a menudo denominadas reglas de exponentes, válido para todos los exponentes enteros, siempre que la base no sea cero:
- bm+n=bm⋅ ⋅ bn()bm)n=bm⋅ ⋅ n()b⋅ ⋅ c)n=bn⋅ ⋅ cn{displaystyle {begin{aligned}b^{m+n} limit=b^{m}cdot ¿Qué?
A diferencia de la suma y la multiplicación, la exponenciación no es conmutativa. Por ejemplo, 23 = 8 ≠ 32 = 9. Además, a diferencia de la suma y la multiplicación, la exponenciación no es asociativa. Por ejemplo, (23)2 = 82 = 64, mientras que 2(32) = 29 = 512. Sin paréntesis, el orden convencional de las operaciones para la exponenciación en serie en notación de superíndice es de arriba hacia abajo (o asociación por la derecha), no de abajo hacia arriba (o asociación por la izquierda). Eso es,
- bpq=b()pq),{displaystyle b^{q}=b^{left(p^{q}right)}
que, en general, es diferente de
- ()bp)q=bpq.{displaystyle left(b^{p}right)^{q}=b^{pq}
Potencias de una suma
Las potencias de una suma normalmente se pueden calcular a partir de las potencias de los sumandos mediante la fórmula binomial
- ()a+b)n=.. i=0n()ni)aibn− − i=.. i=0nn!i!()n− − i)!aibn− − i.{displaystyle (a+b)}=sum ¿Qué? {n}{i}a} {i}b} {n-i}==} ¿Por qué? ¡No!
Sin embargo, esta fórmula es verdadera solo si los sumandos conmutan (es decir, que ab = ba), que es implícitas si pertenecen a una estructura que es conmutativa. De lo contrario, si a y b son, digamos, matrices cuadradas del mismo tamaño, no se puede usar esta fórmula. De ello se deduce que en álgebra computacional, muchos algoritmos que involucran exponentes enteros deben cambiarse cuando las bases de exponenciación no conmutan. Algunos sistemas de álgebra computacional de propósito general usan una notación diferente (a veces ^^ en lugar de ^) para la exponenciación con bases no conmutadas, que entonces se llama potenciación no conmutativa.
Interpretación combinatoria
Para enteros no negativos n y m, el valor de nm es el número de funciones de un conjunto de elementos m a un conjunto de n elementos (ver exponenciación cardinal). Tales funciones se pueden representar como tuplas m de un n-conjunto de elementos (o como m-palabras de letras de un n-letras del alfabeto). Algunos ejemplos de valores particulares de m y n se dan en la siguiente tabla:
nm El nm posible m-tuples de elementos del conjunto {1,... n} 05 = 0 ninguno 14 = 1 (1, 1, 1) 23 = 8 (1, 1, 1), (1, 1, 2), (1, 2, 1), (1, 2, 2), (2, 1, 1), (2, 1, 2), (2, 2, 1), (2, 2, 2), (2, 2, 2) 32 = 9 (1, 1), (1, 2), (1, 3), (2, 1), (2, 2), (2, 3), (3, 1), (3, 2), (3, 3) 41 = 4 1), 2), 3), (4) 50 = 1 ()
Bases particulares
Potencias de diez
En el sistema numérico de base diez (decimal), las potencias enteras de 10 se escriben como el dígito 1 seguido o precedido por un número de ceros determinado por el signo y la magnitud del exponente. Por ejemplo, 103 = 1000 y 10−4 = 0.0001.
La potenciación con base 10 se usa en notación científica para indicar números grandes o pequeños. Por ejemplo, 299792458 m/s (la velocidad de la luz en el vacío, en metros por segundo) se puede escribir como 2.997924 58×108 m/s y luego aproximado como 2.998×108 m/s.
Los prefijos SI basados en potencias de 10 también se utilizan para describir cantidades pequeñas o grandes. Por ejemplo, el prefijo kilo significa 103 = 1000, entonces un kilómetro es 1000 m.
Potencias de dos
Las primeras potencias negativas de 2 se usan comúnmente y tienen nombres especiales, por ejemplo: mitad y cuarto.
Las potencias de 2 aparecen en la teoría de conjuntos, ya que un conjunto con n miembros tiene un conjunto potencia, el conjunto de todos sus subconjuntos, que tiene 2n miembros.
Las potencias enteras de 2 son importantes en informática. Las potencias enteras positivas 2n dan el número de valores posibles para un n-bit número binario entero; por ejemplo, un byte puede tomar 28 = 256 valores diferentes. El sistema numérico binario expresa cualquier número como una suma de potencias de 2 y lo denota como una secuencia de 0 y 1, separados por un punto binario, donde 1 indica una potencia de 2 que aparece en la suma; el exponente está determinado por el lugar de este 1: los exponentes no negativos son el rango del 1 a la izquierda del punto (a partir de 0), y los exponentes negativos están determinados por el rango a la derecha del punto.
Potencias de uno
Cada potencia de uno es igual a: 1n = 1. Esto es cierto incluso si n es negativo.
El primer poder de un número es el número mismo: n1=n.{displaystyle n^{1}=n.}
Potencias de cero
Si el exponente n es positivo (n > 0), la nésima potencia de cero es cero: 0n = 0.
Si el exponente n es negativo (n 0), el npoder de cero 0n es indefinido, porque debe igual 1/0− − n{displaystyle 1/0^{-n} con −n ■ 0, y esto sería 1/0{displaystyle 1/0} según lo anterior.
La expresión 00 se define como 1 o se deja sin definir.
Potencias de uno negativo
Si n es un número entero par, entonces (−1)n = 1. Esto se debe a que un número negativo multiplicado por otro número negativo se cancela y da un número positivo.
Si n es un entero impar, entonces (−1)n = −1. Esto se debe a que quedará un (-1) después de eliminar todos los pares (-1).
Debido a esto, las potencias de −1 son útiles para expresar secuencias alternas. Para una discusión similar de las potencias del número complejo i, consulte § raíces enésimas de un número complejo.
Grandes exponentes
El límite de una secuencia de potencias de un número mayor que uno diverge; en otras palabras, la secuencia crece sin límite:
- bn → como n → cuando b ■ 1
Esto se puede leer como "b elevado a n tiende a +∞ ya que n tiende a infinito cuando b es mayor que uno".
Las potencias de un número con valor absoluto menor que uno tienden a cero:
- bn → 0 como n → cuando SilenciobTENIDA 1
Cualquier poder de uno es siempre uno:
- bn = 1 para todos n si b = 1
Las potencias de –1 alternan entre 1 y –1 como n alterna entre pares e impares y, por lo tanto, no tiende a ningún límite como n crece.
Si b < –1, bn alterna entre mayor y mayor positivo y negativo números como n alternan entre pares e impares, y por lo tanto no tienden a ningún límite como n crece.
Si el número exponenciado varía mientras tiende a 1 cuando el exponente tiende a infinito, entonces el límite no es necesariamente uno de los anteriores. Un caso especialmente importante es
- (1 + 1/n)n → e como n →
Ver § La función exponencial a continuación.
Otros límites, en particular los de las expresiones que toman una forma indeterminada, se describen en § Límites de los poderes a continuación.
Funciones de potencia
Funciones reales de la forma f()x)=cxn{displaystyle f(x)=cx^{n}, donde cل ل 0{displaystyle cneq 0}, a veces se llaman funciones de poder. Cuando n{displaystyle n} es un entero y n≥ ≥ 1{displaystyle ngeq 1}, existen dos familias primarias: n{displaystyle n} incluso, y para n{displaystyle n} extraño. En general 0}" xmlns="http://www.w3.org/1998/Math/MathML">c■0{displaystyle c]0}0" aria-hidden="true" class="mwe-math-fallback-image-inline" src="https://wikimedia.org/api/rest_v1/media/math/render/svg/2ba126f626d61752f62eaacaf11761a54de4dc84" style="vertical-align: -0.338ex; width:5.268ex; height:2.176ex;"/>, cuando n{displaystyle n} Incluso f()x)=cxn{displaystyle f(x)=cx^{n} tenderá hacia la infinidad positiva con el aumento x{displaystyle x}, y también hacia el infinito positivo con disminución x{displaystyle x}. Todos los gráficos de la familia de funciones de poder incluso tienen la forma general Sí.=cx2{displaystyle y=cx^{2}, aplanando más en el medio como n{displaystyle n} aumenta. Funciones con este tipo de simetría ()f()− − x)=f()x){displaystyle f(-x)=f(x)}) se llaman incluso funciones.
Cuando n{displaystyle n} Es extraño. f()x){displaystyle f(x)}'s comportamiento asintotico revierte de positivo x{displaystyle x} a negativo x{displaystyle x}. Para 0}" xmlns="http://www.w3.org/1998/Math/MathML">c■0{displaystyle c]0}0" aria-hidden="true" class="mwe-math-fallback-image-inline" src="https://wikimedia.org/api/rest_v1/media/math/render/svg/2ba126f626d61752f62eaacaf11761a54de4dc84" style="vertical-align: -0.338ex; width:5.268ex; height:2.176ex;"/>, f()x)=cxn{displaystyle f(x)=cx^{n} también tenderá hacia la infinidad positiva con el aumento x{displaystyle x}, pero hacia el infinito negativo con disminución x{displaystyle x}. Todos los gráficos de la familia de funciones de poder extraño tienen la forma general de Sí.=cx3{displaystyle y=cx^{3}, aplanando más en el medio como n{displaystyle n} aumenta y pierde toda la flatness allí en la línea recta para n=1{displaystyle n=1}. Funciones con este tipo de simetría ()f()− − x)=− − f()x){displaystyle f(-x)=-f(x)}) se llaman funciones extrañas.
Para <math alttext="{displaystyle cc.0{displaystyle c realizadas0}<img alt="c , el comportamiento asintotico opuesto es cierto en cada caso.
Tabla de potencias de dígitos decimales
| n | n2 | n3 | n4 | n5 | n6 | n7 | n8 | n9 | n10 |
|---|---|---|---|---|---|---|---|---|---|
| 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 |
| 2 | 4 | 8 | 16 | 32 | 64 | 128 | 256 | 512 | 1024 |
| 3 | 9 | 27 | 81 | 243 | 729 | 2187 | 6561 | 19683 | 59049 |
| 4 | 16 | 64 | 256 | 1024 | 4096 | 16384 | 65536 | 262144 | 1048576 |
| 5 | 25 | 125 | 625 | 3125 | 15625 | 78125 | 390625 | 1953125 | 9765625 |
| 6 | 36 | 216 | 1296 | 7776 | 46656 | 279936 | 1679616 | 10077696 | 60466176 |
| 7 | 49 | 343 | 2401 | 16807 | 117649 | 823543 | 5764801 | 40353607 | 282475249 |
| 8 | 64 | 512 | 4096 | 32768 | 262144 | 2097152 | 16777216 | 134217728 | 1073741824 |
| 9 | 81 | 729 | 6561 | 59049 | 531441 | 4782969 | 43046721 | 387420489 | 3486784401 |
| 10 | 100 | 1000 | 10000 | 100000 | 1000000 | 10000000 | 100000000 | 1000000000 | 10000000000 |
Exponentes racionales
Si x es un número real no negativo, y n es un entero positivo, x1/n{displaystyle x^{1/n} o xn{displaystyle {sqrt[{n}{x}} {fn}} denota la única raíz positiva real nth x, es decir, el número real positivo único Sí. tales que Sí.n=x.{displaystyle y^{n}=x.}
Si x es un número real positivo, y pq{fnMicroc} {} {}}} es un número racional, con p y q 0 enteros, entonces xp/q{textstyle x^{p/q} se define como
- xpq=()xp)1q=()x1q)p.{displaystyle x^{frac {p}=left(x^{p}right) {1}=(x^{frac {1})} {p}
La igualdad del derecho puede derivarse mediante el establecimiento Sí.=x1q,{displaystyle y=x^{frac}{q}} y escritura ()x1q)p=Sí.p=()()Sí.p)q)1q=()()Sí.q)p)1q=()xp)1q.{fnMicrosoft Sans Serif} {fnMicrosoft Sans Serif} {fnMicrosoft Sans Serif} {f}}=m} {c}=c}=left(y^{p}right)}{f} {f} {f} {f} {fnMicroc} {f}}} {f} {f} {f}}}}f}}}}}}}}}}}}f} {f} {f}f}}}}}f} {f} {f}}f}f}f}f}f}f}f}f}f}}f}f}}}}}}}f}f}f}f}f}f}f}f}f}}}}f}f}f}}f}f}f}f}}}}}}fn {1}{q}.}
Si r es un número racional positivo, 0r=0,{displaystyle 0}=0,} por definición.
Todas estas definiciones son necesarias para ampliar la identidad ()xr)s=xrs{displaystyle (x^{r}=x^{rs} a los exponentes racionales.
Por otro lado, hay problemas con la extensión de estas definiciones a bases que no son números reales positivos. Por ejemplo, un número real negativo tiene un real nraíz, que es negativa, si n es extraño, y ninguna raíz real si n es incluso. En este último caso, cualquier complejo na raíz uno elige para x1n,{displaystyle x^{frac {1}{n},} la identidad ()xa)b=xab{displaystyle (x^{a}=x^{ab} no puede estar satisfecho. Por ejemplo,
- ()()− − 1)2)12=112=1ل ل ()− − 1)2⋅ ⋅ 12=()− − 1)1=− − 1.{displaystyle left((-1)^{2}right)^{frac {1}{2}=1}{frac} {2}=1neq (-1)^{2cdot {frac {1}}=(-1)}=-1.}
Consulte § Exponentes reales y § Potencias no enteras de números complejos para obtener detalles sobre cómo se pueden manejar estos problemas.
Exponentes reales
Para números reales positivos, la exponenciación a potencias reales se puede definir de dos maneras equivalentes, ya sea extendiendo las potencias racionales a reales por continuidad (§ Límites de los exponentes racionales, a continuación), o en términos del logaritmo de la base y la función exponencial (§ Potencias a través de logaritmos, a continuación). El resultado siempre es un número real positivo, y las identidades y propiedades que se muestran arriba para exponentes enteros siguen siendo ciertas con estas definiciones para exponentes reales. La segunda definición se usa más comúnmente, ya que se generaliza directamente a exponentes complejos.
Por otro lado, la exponenciación a una potencia real de un número real negativo es mucho más difícil de definir consistentemente, ya que puede no ser real y tener varios valores (ver § Exponentes reales con bases negativas). Se puede elegir uno de estos valores, llamado valor principal, pero no se puede elegir el valor principal para el cual la identidad
- ()br)s=brs{displaystyle left(b^{r}right)}=b^{rs}
es verdad; ver § Falla de identidades de potencia y logaritmo. Por lo tanto, la exponenciación con una base que no es un número real positivo generalmente se ve como una función multivaluada.
Límites de exponentes racionales
Dado que cualquier número irracional puede expresarse como el límite de una secuencia de números racionales, la exponenciación de un número real positivo b con un exponente real arbitrario x se puede definir por continuidad con la regla
- bx=limr()▪ ▪ Q)→ → xbr()b▪ ▪ R+,x▪ ▪ R),{displaystyle b^{x}=lim _{r(in mathbb {Q})to x}b^{r}quad (bin mathbb {R} ^{+},xin mathbb {R}),}}
donde el límite se toma sobre los valores racionales de r únicamente. Este límite existe para cada b positivo y cada x.
Por ejemplo, si x = π, la representación decimales que no termina π = 3.14159... y la monotónica de los poderes racionales se puede utilizar para obtener intervalos ligados por poderes racionales que son tan pequeños como se desee, y debe contener bπ π :{displaystyle b^{pi}:}
- [b3,b4],[b3.1,b3.2],[b3.14,b3.15],[b3.141,b3.142],[b3.1415,b3.1416],[b3.14159,b3.14160],...... {fnMicrosoft Sans Serif}b} {3}b}b}b}b} {3}b}b}b}b} {3}b}b}b}b}b}b} {3}b}b}b}b}b}b}b}b}b}b}b}b}{3}}b}b}b}b}b}b}b}b}{3}{3}{3}}b}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}b}b}b}}b}b}}}}}}b}}}}}}}}}}}b}}}}}}}}}}}}}}}}}}}}b}b}}}}}}}
Por lo tanto, los límites superiores y los límites inferiores de los intervalos forman dos secuencias que tienen el mismo límite, denotadas bπ π .{displaystyle b^{pi}
Esto define bx{displaystyle b^{x} para cada positivo b y reales x como una función continua b y x. Vea también expresión bien definida.
La función exponencial
El función exponencial a menudo se define como x↦ ↦ ex,{displaystyle xmapsto e^{x} Donde e.. 2.718{displaystyle eapprox 2.718} Es el número de Euler. Para evitar el razonamiento circular, esta definición no puede utilizarse aquí. Entonces, una definición de la función exponencial, denotada exp ()x),{displaystyle exp(x),} y del número de Euler se dan, que dependen sólo de la exponencia con exponentes enteros positivos. A continuación se esboza una prueba de que, si se utiliza la definición de exponencia dada en las secciones anteriores, uno tiene
- exp ()x)=ex.{displaystyle exp(x)=e^{x}
Hay muchas formas equivalentes de definir la función exponencial, siendo una de ellas
- exp ()x)=limn→ → JUEGO JUEGO ()1+xn)n.{displaystyle exp(x)=lim _{nrightarrow infty }left(1+{frac {x}{n}right)}{n}}} {n}}
Uno tiene exp ()0)=1,{displaystyle exp(0)=1,} y el identidad exponencial exp ()x+Sí.)=exp ()x)exp ()Sí.){displaystyle exp(x+y)=exp(x)exp(y)} tiene también, desde
- exp ()x)exp ()Sí.)=limn→ → JUEGO JUEGO ()1+xn)n()1+Sí.n)n=limn→ → JUEGO JUEGO ()1+x+Sí.n+xSí.n2)n,{displaystyle exp(x)exp(y)=lim _{nrightarrow infty }left(1+{frac {x}{n}right)}{n}left(1+frac {y} {n}right)}{n}=lim _{nrightarrow infty }left(1+{frac {x+y}{n}+{frac} ¿Qué?
y el segundo mandato xSí.n2{displaystyle {frac {xy}{n^{2}}} no afecta el límite, el rendimiento exp ()x)exp ()Sí.)=exp ()x+Sí.){displaystyle exp(x)exp(y)=exp(x+y)}.
El número de Euler se puede definir como e=exp ()1){displaystyle e=exp(1)}. Se deriva de las ecuaciones anteriores que exp ()x)=ex{displaystyle exp(x)=e^{x} cuando x es un entero (esto resulta de la definición de la multiplicación repetida de la exponentiación). Si x es real, exp ()x)=ex{displaystyle exp(x)=e^{x} resultados de las definiciones dadas en las secciones anteriores, utilizando la identidad exponencial si x es racional, y la continuidad de la función exponencial de otra manera.
El límite que define la función exponencial converge por cada valor complejo de x, y por lo tanto se puede utilizar para ampliar la definición de exp ()z){displaystyle exp(z)}, y así ez,{displaystyle e^{z} de los números reales a cualquier argumento complejo z. Esta función exponencial ampliada aún satisface la identidad exponencial, y es comúnmente utilizada para definir la exponencia para base compleja y exponente.
Potencias vía logaritmos
La definición de ex como función exponencial permite definir bx para cada número real positivo b, en términos de función exponencial y logarítmica. Específicamente, el hecho de que el logaritmo natural ln(x) sea el inverso de la función exponencial e x significa que uno tiene
- b=exp ()In b)=eIn b{displaystyle b=exp(ln b)=e^{ln B}
para todos b ■ 0. Para preservar la identidad ()ex)Sí.=exSí.,{displaystyle (e^{x} {y}=e^{xy}} uno debe tener
- bx=()eIn b)x=exIn b{displaystyle b^{x}=left(e^{ln b}right)^{x}=e^{xln B}
Entonces, exIn b{displaystyle e^{xln b} se puede utilizar como una definición alternativa bx para cualquier real positivo b. Esto coincide con la definición dada anteriormente utilizando exponentes racionales y continuidad, con la ventaja de extenderse directamente a cualquier exponente complejo.
Exponentes complejos con base real positiva
Si b es un número real positivo, la exponenciación con base b y exponente complejo z se define mediante la función exponencial con argumento complejo (ver el final de § La función exponencial, arriba) como
- bz=e()zIn b),{displaystyle b^{z}=e^{(zln b)}}
Donde In b{displaystyle ln b} denota el logaritmo natural de b.
Esto satisface la identidad
- bz+t=bzbt,{displaystyle ¿Qué?
En general, ()bz)t{textstyle left(b^{z}right)}{t} no se define, ya que bz no es un número real. Si se da un significado a la exponencia de un número complejo (ver § Poderes no enteros de números complejos, abajo), uno tiene, en general,
- ()bz)tل ل bzt,{displaystyle left(b^{z}right)}neq b^{zt}
a menos que z sea real o t es un número entero.
Fórmula de Euler,
- eiSí.=# Sí.+ipecado Sí.,{displaystyle e^{iy}=cos y+isin y,}
permite expresar la forma polar de bz{displaystyle b^{z} en términos de las partes reales e imaginarias de z, a saber
- bx+iSí.=bx()# ()Sí.In b)+ipecado ()Sí.In b)),{displaystyle b^{x+iy}=b^{x}(cos(yln b)+isin(yln b)),}
donde el valor absoluto del factor trigonométrico es uno. Esto resulta de
- bx+iSí.=bxbiSí.=bxeiSí.In b=bx()# ()Sí.In b)+ipecado ()Sí.In b)).{displaystyle b^{x+iy}=b^{iy}=b^{x}e^{iyln b}=b^{x}(cos(yln b)+isin(yln b)}
Potencias no enteras de números complejos
En las secciones anteriores, la exponencia con exponentes no enteros se ha definido sólo para bases reales positivas. Para otras bases, las dificultades ya aparecen con el caso aparentemente simple de na raíces, es decir, de exponentes 1/n,{displaystyle 1/n,} Donde n es un entero positivo. Aunque la teoría general de la exponenciación con exponentes no enteros se aplica a na raíces, este caso merece ser considerado primero, ya que no necesita usar logaritmos complejos, y por lo tanto es más fácil de entender.
Raíces enésimas de un número complejo
Todo número complejo distinto de cero z puede escribirse en forma polar como
- z=*** *** eiSilencio Silencio =*** *** ()# Silencio Silencio +ipecado Silencio Silencio ),{displaystyle z=rho e^{itheta }=rho (cos theta +isin theta),}
Donde *** *** {displaystyle rho } es el valor absoluto de z, y Silencio Silencio {displaystyle theta } es su argumento. El argumento se define hasta un número entero de 2π; esto significa que, si Silencio Silencio {displaystyle theta } es el argumento de un número complejo, entonces Silencio Silencio +2kπ π {displaystyle theta +2kpi} es también un argumento del mismo número complejo.
La forma polar del producto de dos números complejos se obtiene multiplicando los valores absolutos y sumando los argumentos. De ello se deduce que la forma polar de una nésima raíz de un número complejo se puede obtener tomando la nésima raíz del valor absoluto y dividiendo su argumento por n:
- ()*** *** eiSilencio Silencio )1n=*** *** neiSilencio Silencio n.{displaystyle left(rho e^{itheta }right)^{frac {fn}={n} {fn}fn},e^{frac {itheta } {n}}
Si 2π π {displaystyle 2pi} se añade a Silencio Silencio {displaystyle theta }, el número complejo no se cambia, pero esto añade 2iπ π /n{displaystyle 2ipi /n} al argumento del na raíz, y proporciona una nueva nraíz. Esto se puede hacer n tiempos, y proporciona el n nlas raíces del número complejo.
Es habitual elegir uno de los n nla raíz como la raíz principal. La elección común es elegir la nraíz de la cual <math alttext="{displaystyle -pi − − π π .Silencio Silencio ≤ ≤ π π ,{displaystyle -pi }<img alt="{displaystyle -pi es decir, nla raíz que tiene la mayor parte real, y, si son dos, la que tiene una parte imaginaria positiva. Esto hace que el principal nth root a continuous function in the whole complex plano, except for negative real values of the radicand. Esta función es igual a la habitual nth root for positive real radicands. Para raíces reales negativas, y exponentes impares, el principal nla raíz no es real, aunque lo habitual nla raíz es real. La continuación analítica muestra que el principal nla raíz es la función diferenciable complejo único que extiende lo habitual nraíz al plano complejo sin los números reales no positivos.
Si el número complejo se mueve alrededor de cero aumentando su argumento, después de un aumento de 2π π ,{displaystyle 2pi} el número complejo vuelve a su posición inicial, y su nlas raíces son permutadas circularmente (son multiplicadas por e2iπ π /nE^{2ipi /n}). Esto demuestra que no es posible definir un nla función raíz que es continua en todo el plano complejo.
Raíces de unidad
Las nésimas raíces de la unidad son las n números complejos tales que wn = 1, donde n es un número entero positivo. Surgen en diversas áreas de las matemáticas, como en la transformada discreta de Fourier o en soluciones algebraicas de ecuaciones algebraicas (resolvente de Lagrange).
El n nlas raíces de la unidad son las n primera potencia de ⋅ ⋅ =e2π π in{displaystyle omega =e^{frac {2ccH00} - Sí., eso es 1=⋅ ⋅ 0=⋅ ⋅ n,⋅ ⋅ =⋅ ⋅ 1,⋅ ⋅ 2,⋅ ⋅ n− − 1.{displaystyle 1=omega ^{0}=omega ^{n},omega =omega ^{1},omega ^{2},omega ^{n-1} El nlas raíces de la unidad que tienen esta propiedad generadora se llaman primitivo nlas raíces de la unidad; tienen la forma ⋅ ⋅ k=e2kπ π in,{displaystyle omega ^{k}=e^{frac {2kpi - Sí. con k coprime con n. La única raíz cuadrada primitiva de la unidad es − − 1;{displaystyle -1;} las cuatro raíces primitivas de la unidad son i{displaystyle i} y − − i.{displaystyle -i.}
Las nésimas raíces de la unidad permiten expresar todas las nésimas raíces de un número complejo z como el estilo n productos de una determinada nésimas raíces de z con una nésima raíz de la unidad.
Geométricamente, las nésimas raíces de la unidad se encuentran en el círculo unitario del plano complejo en los vértices de una n regular -gon con un vértice en el número real 1.
Como número e2kπ π in{displaystyle e^{frac {2kpi - Sí. es el primitivo nla raíz de la unidad con el más pequeño argumento positivo, se llama primitivo nraíz de la unidad, a veces acortado principal nraíz de la unidad, aunque esta terminología puede confundirse con el valor principal de 11/n{displaystyle 1^{1/n} que es 1.
Exponenciación compleja
Definir la exponencia con bases complejas conduce a dificultades similares a las descritas en la sección anterior, excepto que hay, en general, muchos valores posibles para zw.. Por lo tanto, se define un valor principal, que no es continuo para los valores de z que son reales y no positivas, o zw. se define como una función multivalorada.
En todos los casos, el logaritmo complejo se usa para definir la exponenciación compleja como
- zw=ewlog z,{displaystyle z^{w}=e^{wlog z}
Donde log z{displaystyle log z} es la variante del logaritmo complejo que se utiliza, es decir, una función o una función multivalorada tal que
- elog z=z{displaystyle e^{log z}=z}
para cada z en su dominio de definición.
Valor principal
El valor principal del logaritmo complejo es la función única, comúnmente denotada log,{displaystyle log} tal que, por cada número no cero complejo z,
- elog z=z,{displaystyle e^{log z}=z,}
y la parte imaginaria de z satisface
- <math alttext="{displaystyle -pi − − π π .Im≤ ≤ π π .{displaystyle - 'pi' significa 'mathrm {Im} leq pi.}<img alt="{displaystyle -pi
El valor principal del logaritmo complejo no se define para z=0,{displaystyle z=0,} es discontinuo a valores reales negativos z, y es holomorfo (es decir, complejo diferenciable) en otro lugar. Si z es real y positivo, el valor principal del logaritmo complejo es el logaritmo natural: log z=In z.{displaystyle log z=ln z.}
El valor principal zw{displaystyle z^{w} se define como zw=ewlog z,{displaystyle z^{w}=e^{wlog z}Donde log z{displaystyle log z} es el valor principal del logaritmo.
La función ()z,w)→ → zw{displaystyle (z,w)to z^{w} es holomorfa excepto en el barrio de los puntos donde z es real y no positivo.
Si z es real y positivo, el valor principal de zw{displaystyle z^{w} iguala su valor habitual definido anteriormente. Si w=1/n,{displaystyle w=1/n,} Donde n es un entero, este valor principal es el mismo que el definido anteriormente.
Función multivalor
En algunos contextos, hay un problema con la discontinuidad de los valores principales de log z{displaystyle log z} y zw{displaystyle z^{w} en los valores reales negativos de z. En este caso, es útil considerar estas funciones como funciones multivalorizadas.
Si log z{displaystyle log z} denota uno de los valores del logaritmo multivalorado (típicamente su valor principal), los otros valores son 2ikπ π +log z,{displaystyle 2ikpi +log z,} Donde k es cualquier entero. Del mismo modo, si zw{displaystyle z^{w} es un valor de la exponenciación, entonces los otros valores son dados por
- ew()2ikπ π +log z)=zwe2ikπ π w,{displaystyle e^{w(2ikpi +log z)}=z^{w}e^{2ikpi w}
donde k es cualquier número entero.
Diferentes valores de k dar diferentes valores zw{displaystyle z^{w} a) w es un número racional, es decir, hay un entero d tales que ♪ es un entero. Esto resulta de la periodicidad de la función exponencial, más específicamente, que ea=eb{displaystyle e^{a}=e^{b} si a− − b{displaystyle a-b} es un número entero de 2π π i.{displaystyle 2pi i}
Si w=mn{displaystyle w={frac {m} {n}} es un número racional con m y n coprime enteros con 0,}" xmlns="http://www.w3.org/1998/Math/MathML">n■0,{displaystyle n confía0,}0,}" aria-hidden="true" class="mwe-math-fallback-image-inline" src="https://wikimedia.org/api/rest_v1/media/math/render/svg/f2b90cfe174f0cf1c285539df4d03d339af13d87" style="vertical-align: -0.671ex; width:6.302ex; height:2.509ex;"/> entonces zw{displaystyle z^{w} tiene exactamente n valores. En el caso m=1,{displaystyle m=1,} estos valores son los mismos que los descritos en § nth raíces de un número complejo. Si w es un entero, sólo hay un valor que coincide con el de los exponentes del número entero.
La exponenciación multivalorada es holomorfa para zل ل 0,{displaystyle zneq 0,} en el sentido de que su gráfico consta de varias hojas que definen cada una de las funciones holomorfas en el barrio de cada punto. Si z varía continuamente a lo largo de un círculo alrededor 0, entonces, después de un giro, el valor de zw{displaystyle z^{w} ha cambiado de hoja.
Cálculo
El forma canónica x+iSí.{displaystyle x+iy} de zw{displaystyle z^{w} se puede calcular de la forma canónica de z y w. Aunque esto puede ser descrito por una sola fórmula, es más claro dividir el cálculo en varios pasos.
- Forma polar de z. Si z=a+ib{displaystyle z=a+ib} es la forma canónica de z ()a y b siendo real), entonces su forma polar es Donde *** *** =a2+b2{displaystyle rho ={2}}} y Silencio Silencio =atan2 ()a,b){displaystyle theta =operatorname {atan2} (a,b)} (ver atan2 para la definición de esta función).z=*** *** eiSilencio Silencio =*** *** ()# Silencio Silencio +ipecado Silencio Silencio ),{displaystyle z=rho e^{itheta }=rho (cos theta +isin theta),}
- Logaritmo de z. El valor principal de este logaritmo es log z=In *** *** +iSilencio Silencio ,{displaystyle log z=ln rho +itheta} Donde In{displaystyle ln } denota el logaritmo natural. Los otros valores del logaritmo se obtienen añadiendo 2ikπ π {displaystyle 2ikpi} para cualquier entero k.
- Forma canónica de wlog z.{displaystyle wlog z.} Si w=c+di{displaystyle w=c+di} con c y d reales, los valores de wlog z{displaystyle wlog z} son el valor principal correspondiente k=0.{displaystyle k=0.}wlog z=()cIn *** *** − − dSilencio Silencio − − 2dkπ π )+i()dIn *** *** +cSilencio Silencio +2ckπ π ),{displaystyle wlog z=(cln rho -dtheta -2dkpi)+i(dln rho +ctheta +2ckpi),}
- Resultado final. Utilizando las identidades ex+Sí.=exeSí.{displaystyle e^{x+y}=e^{x}e^{y} y eSí.In x=xSí.,{displaystyle e^{yln x}=x^{y} uno se pone con k=0{displaystyle k=0} por el valor principal.zw=*** *** ce− − d()Silencio Silencio +2kπ π )()# ()dIn *** *** +cSilencio Silencio +2ckπ π )+ipecado ()dIn *** *** +cSilencio Silencio +2ckπ π )),{displaystyle z^{w}=rho ^{c}e^{-d(theta +2kpi)}left(cos(dln rho +ctheta +2ckpi)+isin(dln rho +ctheta +2ckpi)right),}
Ejemplos
- ii{displaystyle i^{i}
La forma polar de i es i=eiπ π /2,{displaystyle i=e^{ipi /2} y los valores de log i{displaystyle log i} asíDe ello se desprende quelog i=i()π π 2+2kπ π ).{displaystyle log i=ileft({frac {pi }}+2kpi right).}Entonces, todos los valores ii{displaystyle i^{i} son reales, el principal siendoii=eilog i=e− − π π 2e− − 2kπ π .{displaystyle i^{i}=e^{ilog i}=e^{-{frac {pi} ♫ {2}e^{-2kpi }e− − π π 2.. 0.2079.{displaystyle e^{fc {fnMicroc} 0.2079. - ()− − 2)3+4i{displaystyle (-2)^{3+4i}
Del mismo modo, la forma polar de −2 es − − 2=2eiπ π .{displaystyle -2=2e^{ipi } Así, el método descrito anteriormente da los valoresEn este caso, todos los valores tienen el mismo argumento 4In 2,{displaystyle 4ln 2,} y diferentes valores absolutos.()− − 2)3+4i=23e− − 4()π π +2kπ π )()# ()4In 2+3()π π +2kπ π ))+ipecado ()4In 2+3()π π +2kπ π )))=− − 23e− − 4()π π +2kπ π )()# ()4In 2)+ipecado ()4In 2)).{4}4icH00cH00cH00}icH00cH00cH00}(c4ccH00)}(ccn2iiccH0}cciiiiiccH3cH0}cH0cH0cH3cH3cH3cH3cH3cH3p]
En ambos ejemplos, todos los valores zw{displaystyle z^{w} tienen el mismo argumento. Más generalmente, esto es cierto si y sólo si la parte real de w es un entero.
Fallo de identidades de potencia y logaritmo
Algunas identidades para potencias y logaritmos para números reales positivos fallarán para números complejos, sin importar cómo las potencias complejas y los logaritmos complejos se definan como funciones de un solo valor. Por ejemplo:
- La identidad log(bx) x ⋅ logb siempre b es un número real positivo y x es un número real. Pero para la rama principal del logaritmo complejo uno tiene
log ()()− − i)2)=log ()− − 1)=iπ π ل ل 2log ()− − i)=2log ()e− − iπ π /2)=2− − iπ π 2=− − iπ π {displaystyle log(-i)^{2})=log(-1)=ipi neq 2log(-i)=2log(e^{-ipi /2})=2,{frac {-ipi} } {2}=-ipi }
Independientemente de cuál rama del logaritmo se utiliza, existirá un fallo similar de la identidad. Lo mejor que se puede decir (si sólo utiliza este resultado) es que:
log wz↑ ↑ zlog w()mod2π π i){displaystyle log w^{z}equiv zlog w{pmod {2pi}}}Esta identidad no se mantiene ni siquiera al considerar el registro como una función multivalorada. Los posibles valores log(wz) contener los z ⋅ logw como subconjunto adecuado. Uso Log(w) para el valor principal log(w) y m, n los posibles valores de ambos lados son:
{}log wz}={}z⋅ ⋅ Log w+z⋅ ⋅ 2π π in+2π π im▪ ▪ m,n▪ ▪ Z}{}zlog w}={}zLog w+z⋅ ⋅ 2π π in▪ ▪ n▪ ▪ Z}{displaystyle {begin{aligned}left{log w^{z}right=left{zcdot nombre del operador {Log} w+zcdot 2pi} in+2pi immid m,nin mathbb {Z} right\\left{zlog wright {cHFF} {Log} w+zcdot 2pi inmid nin mathbb {Z} rightend{aligned}}} - Las identidades ()bc)x = bxcx y ()b/c)x = bx/cx son válidos cuando b y c son números reales positivos y x es un número real. Pero, para los valores principales, uno tiene
y()− − 1⋅ ⋅ − − 1)12=1ل ل ()− − 1)12()− − 1)12=− − 1{displaystyle (-1cdot -1)^{frac {1}{2}=1neq (-1)^{frac {1}{2}}(-1)^{frac {1}{2}=-1}Por otro lado, cuando x es un entero, las identidades son válidas para todos los números complejos no cero. Si la exponentiación se considera como una función multivalorada, entonces los posibles valores de (1 - ⋅ −1)1/2 son {1, −1}. La identidad sostiene, pero diciendo {1} = {1 ⋅ −1)1/2Está mal.()1− − 1)12=()− − 1)12=iل ل 112()− − 1)12=1i=− − i{displaystyle left({frac {1}right)}{frac {1}{2}=(-1)^{frac {1}{2}=ineq {frac {1}{frac}=ineq {fc} {fc} {fc} {fc} {fc} {f} {fn} {fn} {f}}} {f}f} {fn}f}f}f}f}f}f}f}f}f}f}f}f}f}f}f}f}f}f}f}f}f}f}f}f}f}f}f}f}f}f}f}f}fnfnfnfnf}fnf}fnfnfnfnf}fnfnfnfnfnfnfnfnf}fnfnf}fn {1}{(-1)}{frac {1}{2}}={frac} {1}{i}=-i}
- La identidad ()ex)Sí. = exy mantiene para números reales x y Sí., pero suponiendo su verdad para números complejos conduce a la siguiente paradoja, descubierta en 1827 por Clausen:
Para cualquier entero n, tenemos:
- e1+2π π in=e1e2π π in=e⋅ ⋅ 1=e{displaystyle e^{1+2pi ################################################################################################################################################################################################################################################################ # Intento #
- ()e1+2π π in)1+2π π in=e{displaystyle left(e^{1+2pi in}right)^{1+2pi in}=eqquad } (tomar la ()1+2π π in){displaystyle (1+2pi in)}-la potencia de ambos lados)
- e1+4π π in− − 4π π 2n2=e{displaystyle e^{1+4pi in-4pi ^{2}n^{2}=eqquad } (usando) ()ex)Sí.=exSí.{displaystyle left(e^{x}right)} {y}=e^{xy} y expandiendo el exponente)
- e1e4π π ine− − 4π π 2n2=e{displaystyle e^{1}e^{4pi ################################################################################################################################################################################################################################################################ ^{2}n^{2}=eqquad } (usando) ex+Sí.=exeSí.{displaystyle e^{x+y}=e^{x}e^{y})
- e− − 4π π 2n2=1{displaystyle e^{-4pi ^{2}n^{2}=1qquad } (dividiendo por e)
Por lo tanto, cuando se expande el exponente, se supone implícitamente que log exp z=z{displaystyle log exp z=z} para valores complejos z, que está mal, ya que el logaritmo complejo es multivalorado. En otras palabras, la identidad equivocada ()ex)Sí. = exy debe ser reemplazado por la identidadexp ()()1+2π π in)log exp ()1+2π π in))=exp ()1+2π π in).{displaystyle exp left(1+2pi in)log exp(1+2pi in)right)=exp(1+2pi in).}que es una verdadera identidad entre funciones multivaloradas.()ex)Sí.=eSí.log ex,{displaystyle left(e^{x}right)}{y}=e^{ylog e^{x}}
Irracionalidad y trascendencia
Si b es un número algebraico real positivo, y x es un número racional, entonces bx es un número algebraico. Esto resulta de la teoría de extensiones algebraicas. Esto sigue siendo cierto si b es cualquier número algebraico, en cuyo caso, todos los valores de bx (como una función multivaluada) son algebraicas. Si x es irracional (es decir, no racional), y ambos b y x son algebraicos, teorema de Gelfond-Schneider afirma que todos los valores de bx son trascendentales (es decir, no algebraicos), excepto si b es igual a 0 o 1 .
En otras palabras, si x es irracional y b∉{}0,1},{displaystyle bnot in {0,1},} entonces al menos uno de b, x y bx es trascendental.
Potencias enteras en álgebra
La definición de exponentiación con exponentes enteros positivos como multiplicación repetida puede aplicarse a cualquier operación asociativa denotada como una multiplicación. La definición de x0{displaystyle x^{0} requiere además la existencia de una identidad multiplicativa.
Una estructura algebraica que consta de un conjunto junto con una operación asociativa denotada multiplicativamente, y una identidad multiplicativa denotada por 1 es un monoide. En tal monoide, la exponenciación de un elemento x se define inductivamente por
- x0=1,{displaystyle x^{0}=1,}
- xn+1=xxn{displaystyle x^{n+1}=xx^{n} para cada entero no negativo n.
Si n es un entero negativo, xn{displaystyle x^{n} se define solamente si x tiene un inverso multiplicativo. En este caso, el inverso de x es denotado x− − 1,{displaystyle x^{-1},} y xn{displaystyle x^{n} se define como ()x− − 1)− − n.{displaystyle left(x^{-1}right)}{-n}
La potenciación con exponentes enteros obedece a las siguientes leyes, para x y y en la estructura algebraica, y m y n enteros:
- x0=1xm+n=xmxn()xm)n=xmn()xSí.)n=xnSí.nsixSí.=Sí.x,y, en particular, si la multiplicación es conmutativa.{fnMicrosoft Sans Serif} {fnMicrosoft Sans Serif} {fnMicrosoft Sans Serif} {fn} {fn}cfn} {fn}cH0}cH00}cH00}cH009cH00}cH009cH00cH009cH00}cH00cH009cH009cH00cH00cH009cH009cH009cH00cH00cH00cH009cH009cH00}cH00cH009cH00cH009cH00cH009cH00}cH00cH00cH00cH00cH00}cH00}cH009cH009cH009cH00cH009cH009cH00
Estas definiciones se usan ampliamente en muchas áreas de las matemáticas, especialmente para grupos, anillos, campos, matrices cuadradas (que forman un anillo). Se aplican también a funciones de un conjunto a sí mismo, que forman un monoide bajo composición de funciones. Esto incluye, como instancias específicas, transformaciones geométricas y endomorfismos de cualquier estructura matemática.
Cuando hay varias operaciones que pueden repetirse, es común indicar la operación repetida colocando su símbolo en el superscript, antes del exponente. Por ejemplo, si f es una función real cuyo valor se puede multiplicar, fn{displaystyle f^{n} denota la exponenciación con respecto a la multiplicación, y f∘ ∘ n{displaystyle f^{fnMicrosoft No. puede denotar la exponencia con respecto a la composición de la función. Eso es,
- ()fn)()x)=()f()x))n=f()x)f()x)⋯ ⋯ f()x),{displaystyle (f^{n})(x)=(f(x)^{n}=f(x),f(x)cdots f(x),}
y
- ()f∘ ∘ n)()x)=f()f()⋯ ⋯ f()f()x))⋯ ⋯ )).{displaystyle (f^{circ n})(x)=f(cdots f(f(x))cdots)). }
Comúnmente, ()fn)()x){displaystyle (f^{n})(x)} es denotado f()x)n,{displaystyle f(x)^{n} mientras ()f∘ ∘ n)()x){displaystyle (f^{circ n})(x)} es denotado fn()x).{displaystyle f^{n}(x). }
En grupo
Un grupo multiplicativo es un conjunto con una operación asociativa denotada como multiplicación, que tiene un elemento identidad, y tal que cada elemento tiene un inverso.
Entonces, si G es un grupo, xn{displaystyle x^{n} se define para cada x▪ ▪ G{displaystyle xin G} y cada entero n.
El conjunto de todos los poderes de un elemento de grupo forman un subgrupo. Un grupo (o subgrupo) que consiste en todos los poderes de un elemento específico x es el grupo cíclico generado por x. Si todos los poderes de x son distintos, el grupo es isomorfo al grupo aditivo Z{displaystyle mathbb {Z} de los enteros. De lo contrario, el grupo cíclico es finito (tiene un número finito de elementos), y su número de elementos es el orden de x. Si el orden x es n, entonces xn=x0=1,{displaystyle x^{n}=x^{0}=1,} y el grupo cíclico generado por x consiste en n primera potencia de x (comenzando indiferentemente desde el exponente 0 o 1).
El orden de los elementos juega un papel fundamental en la teoría de grupos. Por ejemplo, el orden de un elemento en un grupo finito es siempre un divisor del número de elementos del grupo (el orden del grupo). Los posibles órdenes de elementos de grupo son importantes en el estudio de la estructura de un grupo (ver teoremas de Sylow) y en la clasificación de grupos finitos simples.
La notación de superscripto también se utiliza para la conjugación; es decir, gh = h−1gh, donde g y h son elementos de un grupo. Esta notación no puede confundirse con la exponenciación, ya que el superscripto no es un entero. La motivación de esta notación es que la conjugación obedece algunas de las leyes de la exponencia, es decir, ()gh)k=ghk{displaystyle (g^{h}=g^{hk}} y ()gh)k=gkhk.{displaystyle (gh)}=g^{k}h^{k}}
En un cuadrilátero
En un anillo, puede ocurrir que algunos elementos no cero satisfagan xn=0{displaystyle x^{n}=0} para algunos enteros n. Se dice que tal elemento es nilpotente. En un anillo comunicativo, los elementos nilpotent forman un ideal, llamado nilradical del anillo.
Si el nilradical se reduce al cero ideal (es decir, si xل ل 0{displaystyle xneq 0} implicación xnل ل 0{displaystyle x^{n}neq 0} para cada entero positivo n), el anillo conmutativo se dice reducido. Anillos reducidos importantes en geometría algebraica, ya que el anillo de coordenadas de un conjunto algebraico afine es siempre un anillo reducido.
Más generalmente, dado un ideal I en un anillo conmutativo R, el conjunto de los elementos de R que tienen un poder en I es un ideal, llamado el radical I. El nilradical es el radical del ideal cero. Un ideal radical es un ideal que iguala a su propio radical. En un anillo polinomio k[x1,...... ,xn]{displaystyle k[x_{1},ldotsx_{n}} sobre un terreno k, un ideal es radical si y sólo si es el conjunto de todos los polinomios que son cero en un conjunto algebraico afine (esto es una consecuencia de la Nullstellensatz de Hilbert).
Matrices y operadores lineales
Si A es una matriz cuadrada, luego el producto de A con sí mismo n tiempos se llama el poder de la matriz. También A0{displaystyle A^{0} se define como la matriz de identidad, y si A es invertible, entonces A− − n=()A− − 1)n{displaystyle A^{-n}=left(A^{-1}right).
Los poderes de matriz aparecen a menudo en el contexto de sistemas dinámicos discretos, donde la matriz A expresa una transición de un vector estatal x de algún sistema al siguiente estado Ax del sistema. Esta es la interpretación estándar de una cadena Markov, por ejemplo. Entonces... A2x{displaystyle A^{2}x} es el estado del sistema después de dos pasos del tiempo, y así sucesivamente: Anx{displaystyle A^{n}x} es el estado del sistema después n pasos de tiempo. El poder de la matriz An{displaystyle A^{n} es la matriz de transición entre el estado ahora y el estado en un momento n pasos en el futuro. Así que los poderes de matriz de cálculo es equivalente a la solución de la evolución del sistema dinámico. En muchos casos, los poderes de matriz se pueden calcular de manera conveniente utilizando eigenvalues y eigenvectores.
Aparte de las matrices, los operadores lineales más generales también pueden ser exponentes. Un ejemplo es el operador derivado del cálculo, d/dx{displaystyle d/dx}, que es un operador lineal que actúa en funciones f()x){displaystyle f(x)} para dar una nueva función ()d/dx)f()x)=f.()x){displaystyle (d/dx)f(x)=f'(x)}. El n-la potencia del operador de diferenciación es el n-th derivative:
- ()ddx)nf()x)=dndxnf()x)=f()n)()x).{displaystyle left({frac {d} {dx}derecha)} {n}f(x)={frac {d^{n}{n}}f(x)=f^{(n)}(x). }
Estos ejemplos son para exponentes discretos de operadores lineales, pero en muchas circunstancias también es deseable definir potencias de dichos operadores con exponentes continuos. Este es el punto de partida de la teoría matemática de los semigrupos. Así como el cálculo de potencias de matriz con exponentes discretos resuelve sistemas dinámicos discretos, el cálculo de potencias de matriz con exponentes continuos resuelve sistemas con dinámica continua. Los ejemplos incluyen enfoques para resolver la ecuación del calor, la ecuación de Schrödinger, la ecuación de onda y otras ecuaciones diferenciales parciales, incluida una evolución temporal. El caso especial de exponenciar el operador derivada a una potencia no entera se denomina derivada fraccionaria que, junto con la integral fraccionaria, es una de las operaciones básicas del cálculo fraccionario.
Campos finitos
Un campo es una estructura algebraica en la que la multiplicación, la suma, la resta y la división se definen y satisfacen las propiedades de que la multiplicación es asociativa y cada elemento distinto de cero tiene un inverso multiplicativo. Esto implica que la exponenciación con exponentes enteros está bien definida, excepto para potencias no positivas de 0. Ejemplos comunes son los números complejos y sus subcampos, los números racionales y los números reales, que se han considerado anteriormente en este artículo, y son todos infinitos.
A campo finito es un campo con un número finito de elementos. Este número de elementos es un número primario o un poder primario; es decir, tiene la forma q=pk,{displaystyle q=p^{k},} Donde p es un número primo, y k es un entero positivo. Por todos esos q, hay campos con q elementos. Los campos con q todos los elementos son isomorfos, lo que permite, en general, trabajar como si hubiera sólo un campo con q elementos, denotados Fq.{displaystyle mathbb {F} _{q}
Uno tiene
- xq=x{displaystyle x^{q}=x}
para todos x▪ ▪ Fq.{displaystyle xin mathbb {F} _{q}
Un elemento primitivo en Fq{displaystyle mathbb {F} _{q} es un elemento g tal que el conjunto de q − 1 primera potencia de g (es decir, {}g1=g,g2,...... ,gp− − 1=g0=1}{displaystyle {1}=g,g^{2},ldotsg^{p-1}=g^{0}=1}}) iguala el conjunto de los elementos no cero de Fq.{displaystyle mathbb {F} _{q} Hay φ φ ()p− − 1){displaystyle varphi (p-1)} elementos primitivos en Fq,{displaystyle mathbb {F} _{q},} Donde φ φ {displaystyle varphi } es la función totiente de Euler.
In Fq,{displaystyle mathbb {F} _{q},} la identidad del sueño de Freshman
- ()x+Sí.)p=xp+Sí.p{displaystyle (x+y)}=x^{p}+y^{p}
es verdad para el exponente p. As xp=x{displaystyle x^{p}=x} dentro Fq,{displaystyle mathbb {F} _{q},} Se deduce que el mapa
- F:: Fq→ → Fqx↦ ↦ xp{displaystyle {begin{aligned} Fcolon {} {}mathbb {F} _{q}to mathbb {F} _{q}\\\\\\cH00to #
es lineal Fq,{displaystyle mathbb {F} _{q},} y es un automorfismo de campo, llamado el automorfismo Frobenius. Si q=pk,{displaystyle q=p^{k},} sobre el terreno Fq{displaystyle mathbb {F} _{q} tiene k automorfismos, que son los k primera potencia (bajo composición) de F. En otras palabras, el grupo Galois de Fq{displaystyle mathbb {F} _{q} es ciclo de orden k, generado por el automorfismo Frobenius.
El intercambio clave Diffie-Hellman es una aplicación de exponenciación en campos finitos que se utiliza ampliamente para comunicaciones seguras. Utiliza el hecho de que la exponencia es computacionalmente barata, mientras que la operación inversa, el logaritmo discreto, es computacionalmente costoso. Más precisamente, si g es un elemento primitivo Fq,{displaystyle mathbb {F} _{q},} entonces ge{displaystyle g^{e} se puede computar eficientemente con exponentiation por squaring para cualquier e, incluso si q es grande, mientras que no hay un algoritmo conocido que permite recuperar e desde ge{displaystyle g^{e} si q es suficientemente grande.
Potencias de conjuntos
El producto cartesiano de dos sets S y T es el conjunto de los pares ordenados ()x,Sí.){displaystyle (x,y)} tales que x▪ ▪ S{displaystyle xin S} y Sí.▪ ▪ T.{displaystyle yin T.} Esta operación no es adecuadamente comunicativa ni asociativa, pero tiene estas propiedades hasta isomorfismos canónicos, que permiten identificar, por ejemplo, ()x,()Sí.,z)),{displaystyle (x,(y,z)),} ()()x,Sí.),z),{displaystyle (x,y),z),} y ()x,Sí.,z).{displaystyle (x,y,z). }
Esto permite definir el npoder Sn{displaystyle S^{n} de un conjunto S como el conjunto de todos n-tuples ()x1,...... ,xn){displaystyle (x_{1},ldotsx_{n}} de elementos de S.
Cuando S está dotado de alguna estructura, es frecuente que Sn{displaystyle S^{n} es naturalmente dotado con una estructura similar. En este caso, el término "producto directo" se utiliza generalmente en lugar de "producto cartesiano", y la exponencia denota la estructura del producto. Por ejemplo Rn{displaystyle mathbb {R} {} {}} {fn}} (donde) R{displaystyle mathbb {R} denota los números reales) denota el producto cartesiano de n copias de R,{displaystyle mathbb {R} así como su producto directo como espacio vectorial, espacios topológicos, anillos, etc.
Conjuntos como exponentes
A n-tuple ()x1,...... ,xn){displaystyle (x_{1},ldotsx_{n}} de elementos de S puede considerarse como una función desde {}1,...... ,n}.{displaystyle {1,ldotsn} Esto se generaliza a la siguiente notación.
Dados dos sets S y T, el conjunto de todas las funciones de T a S es denotado ST{displaystyle S^{T}. Esta notación exponencial está justificada por los siguientes isomorfismos canónicos (para el primero, vea Currying):
- ()ST)U.. ST× × U,{displaystyle (S^{T})}cong S^{Ttimes U}
- ST⊔ ⊔ U.. ST× × SU,{displaystyle S^{Tsqcup U}cong S^{T}times S^{U}
Donde × × {displaystyle times } denota el producto cartesiano, y ⊔ ⊔ {displaystyle sqcup } la unión descomunal.
Se puede utilizar como exponentes para otras operaciones en conjuntos, típicamente para sumas directas de grupos abelianos, espacios vectoriales o módulos. Para distinguir las sumas directas de productos directos, el exponente de una suma directa se coloca entre paréntesis. Por ejemplo, RN{displaystyle mathbb {R} {N} denota el espacio vectorial de las secuencias infinitas de números reales, y R()N){displaystyle mathbb {R} {cH00}} el espacio vectorial de esas secuencias que tienen un número finito de elementos no cero. Este último tiene una base que consiste en las secuencias con exactamente un elemento no cero que equivale 1, mientras que las bases Hamel de la primera no se pueden describir explícitamente (porque su existencia implica la lema de Zorn).
En este contexto, 2 puede representar el conjunto {}0,1}.{displaystyle {0,1} Entonces, 2S{displaystyle 2^{S} denota el conjunto de poder S, ese es el conjunto de las funciones de S a {}0,1},{displaystyle {0,1},} que se puede identificar con el conjunto de los subconjuntos de S, mediante la asignación de cada función a la imagen inversa 1.
Esto encaja con la exponenciación de los números cardinales, en el sentido de que |ST| = |S||T|, donde |X| es la cardinalidad de X.
En teoría de categorías
En la categoría de conjuntos, los morfismos entre conjuntos X y Y son las funciones de X a Y. Resulta que el conjunto de funciones de X a Y que se denota YX{displaystyle Y^{X} en la sección anterior también se puede denotar hom ()X,Y).{displaystyle hom(X,Y).} El isomorfismo ()ST)U.. ST× × U{displaystyle (S^{T}cong S^{Ttimes U} puede ser reescrito
- hom ()U,ST).. hom ()T× × U,S).{displaystyle hom(U,S^{T})cong hom(Ttimes U,S).}
Esto significa que el funtor "exponenciación a la potencia T " es un adjunto derecho del funtor "producto directo con T ".
Esto generaliza la definición de exponencia en una categoría en la que existen productos directos finitos: en tal categoría, el functor X→ → XT{displaystyle Xto X^ {T} es, si existe, un derecho unido al functor Y→ → T× × Y.{displaystyle Yto Ttimes Y.} Una categoría se llama Categoría cerrada cartesiana, si existen productos directos, y el functor Y→ → X× × Y{displaystyle Yto Xtimes Sí. tiene un derecho de unión para cada T.
Exponenciación repetida
Así como la exponenciación de números naturales está motivada por la multiplicación repetida, es posible definir una operación basada en la exponenciación repetida; esta operación a veces se denomina hiper-4 o tetración. La iteración de la tetración conduce a otra operación, y así sucesivamente, un concepto llamado hiperoperación. Esta secuencia de operaciones se expresa mediante la función de Ackermann y la notación de flecha hacia arriba de Knuth. Así como la exponenciación crece más rápido que la multiplicación, que crece más rápido que la suma, la tetración crece más rápido que la exponenciación. Evaluadas en (3, 3), las funciones suma, multiplicación, exponenciación y tetración producen 6, 9, 27 y 7625597484987 (= 327 = 333 = 33) respectivamente.
Límites de poderes
Cero a la potencia de cero da una serie de ejemplos de límites que son de la forma indeterminada 00. Los límites en estos ejemplos existen, pero tienen valores diferentes, lo que demuestra que la función de dos variables xy no tiene límite en el punto (0, 0). Uno puede considerar en qué puntos esta función tiene un límite.
Más precisamente, considere la función f()x,Sí.)=xSí.{displaystyle f(x,y)=x^{y} definidas 0}}" xmlns="http://www.w3.org/1998/Math/MathML">D={}()x,Sí.)▪ ▪ R2:x■0}{displaystyle D={(x,y)in mathbf [R] ^{2}:x confianza0}0}}" aria-hidden="true" class="mwe-math-fallback-image-inline" src="https://wikimedia.org/api/rest_v1/media/math/render/svg/2bb3ae1d04fc8a4e673d1694da043dfc7fc77193" style="vertical-align: -0.838ex; width:26.102ex; height:3.176ex;"/>. Entonces... D se puede ver como un subconjunto de R2 (es decir, el conjunto de todos los pares ()x, Sí.) con x, Sí. perteneciente a la línea de números reales ampliados R = [ — jóvenes, + personas], dotado con la topología del producto), que contendrá los puntos en los que la función f tiene un límite.
De hecho, f tiene un límite en todos los puntos de acumulación de D , excepto (0, 0), (+∞, 0), (1, +∞) y (1, −∞). En consecuencia, esto permite definir las potencias xy por continuidad siempre que 0 ≤ x ≤ +∞, −∞ ≤ y ≤ +∞, excepto 00 , (+∞)0, 1+∞ y 1−∞, que siguen siendo formas indeterminadas.
Bajo esta definición por continuidad, obtenemos:
- x+ = + dieta y xJUEGO = 0, cuando 1 x ≤ + dieta.
- x+ = 0 y xJUEGO = + dieta, cuando 0 ≤ x 1.
- 0Sí. = 0 y (+∞)Sí. = + dieta, cuando 0 Sí. ≤ + dieta.
- 0Sí. = + dieta y (+∞)Sí. = 0, cuando −∞ ≤ Sí. 0.
Estas potencias se obtienen tomando límites de xy para valores positivos de x. Este método no permite una definición de xy cuando x < 0, ya que empareja (x, y) con x < 0 no son puntos de acumulación de D.
Por otro lado, cuando n es un número entero, la potencia xn ya es significativo para todos los valores de x, incluido el negativo unos. Esto puede hacer que la definición 0n = +∞ obtenida arriba para n problemático cuando n es impar, ya que en este caso xn → +∞ como x tiende a 0 a través de valores positivos, pero no negativos.
Cálculo eficiente con exponentes enteros
Calcular bn usando la multiplicación iterada requiere n − 1 operaciones de multiplicación, pero se puede calcular de manera más eficiente que eso, como se ilustra en el siguiente ejemplo. Para calcular 2100, aplique la regla de Horner al exponente 100 escrito en binario:
- 100=22+25+26=22()1+23()1+2)){displaystyle 100=2^{2}+2^{5}+2^{6}=2^{2}(1+2^{3}(1+2)}.
Luego calcula los siguientes términos en orden, leyendo la regla de Horner de derecha a izquierda.
| 22 = 4 |
| 22) = 23 = 8 |
| (22)3)2 = 26 = 64 |
| (22)6)2 = 212 = 4096 |
| (22)12)2 = 224 = 16777216 |
| 224) = 225 = 33554432 |
| (22)25)2 = 250 = 1125899906842624 |
| (22)50)2 = 2100 = 1267650600228229401496703205376 |
Esta serie de pasos solo requiere 8 multiplicaciones en lugar de 99.
En general, el número de operaciones de multiplicación requeridas para calcular bn puede reducirse ▪ ▪ n+⌊ ⌊ log2 n⌋ ⌋ − − 1,{displaystyle sharp n+lfloor log _{2}nrfloor -1. utilizando la exponenciación por squaring, donde ▪ ▪ n{displaystyle sharp n} denota el número de 1 en la representación binaria de n. Para algunos exponentes (100 no está entre ellos), el número de multiplicaciones se puede reducir aún más mediante la computación y el uso de la mínima exponente de cadena de adición. Encontrar el mínimo secuencia de multiplicaciones (la cadena de adición de longitud mínima para el exponente) para bn es un problema difícil, para el cual no se conocen algoritmos eficientes (véase el problema de la suma Subset), pero hay muchos algoritmos heurísticos razonablemente eficientes disponibles. Sin embargo, en computaciones prácticas, la exponentiación por squaring es lo suficientemente eficiente, y mucho más fácil de implementar.
Funciones iteradas
La composición de la función es una operación binaria que se define en funciones tales que el codominio de la función escrita a la derecha se incluye en el dominio de la función escrita a la izquierda. Está denotado g∘ ∘ f,{displaystyle gcirc f,} y definidas
- ()g∘ ∘ f)()x)=g()f()x)){displaystyle (gcirc f)(x)=g(f(x)}
para cada x en el dominio de f.
Si el dominio de una función f iguala su codominio, uno puede componer la función con sí mismo un número arbitrario de tiempo, y esto define el na potencia de la función bajo composición, comúnmente llamada nt iterate de la función. Así fn{displaystyle f^{n} denota generalmente el nt iterate of f; por ejemplo, f3()x){displaystyle f^{3}(x)} medios f()f()f()x))).{displaystyle f(f(f(x))). }
Cuando una multiplicación se define en el codominio de la función, esto define una multiplicación en las funciones, la multiplicación de punta, que induce otra exponentiación. Al utilizar notación funcional, los dos tipos de exponentiación se distinguen generalmente colocando el exponente de la iteración funcional antes los paréntesis cerrando los argumentos de la función, y colocando el exponente de la multiplicación de punta después los paréntesis. Así f2()x)=f()f()x)),{displaystyle f^{2}(x)=f(x)} y f()x)2=f()x)⋅ ⋅ f()x).{displaystyle f(x)^{2}=f(x)cdot f(x).} Cuando la notación funcional no se utiliza, la desambiguación se hace a menudo colocando el símbolo de composición ante el exponente; por ejemplo f∘ ∘ 3=f∘ ∘ f∘ ∘ f,{displaystyle f^{circ 3}=fcirc fcirc f} y f3=f⋅ ⋅ f⋅ ⋅ f.{displaystyle f^{3}=fcdot fcdot f.} Por razones históricas, el exponente de una multiplicación repetida se coloca ante el argumento de algunas funciones específicas, típicamente las funciones trigonométricas. Entonces, pecado2 x{displaystyle sin ^{2}x} y pecado2 ()x){displaystyle sin ^{2}(x)} ambos significan pecado ()x)⋅ ⋅ pecado ()x){displaystyle sin(x)cdot sin(x)} y no pecado ()pecado ()x)),{displaystyle sin(sin(x)),} que, en cualquier caso, rara vez se considera. Históricamente, varias variantes de estas notaciones fueron utilizadas por diferentes autores.
En este contexto, el exponente − − 1{displaystyle -1} denota siempre la función inversa, si existe. Así que... pecado− − 1 x=pecado− − 1 ()x)=arcsin x.{displaystyle sin ^{-1}x=sin ^{-1}(x)=arcsin x.} Para las fracciones inversas multiplicativas se utilizan generalmente como en 1/pecado ()x)=1pecado x.{displaystyle 1/sin(x)={frac {1}{sin x}}
En lenguajes de programación
Los lenguajes de programación generalmente expresan la exponenciación como un operador infijo o como una aplicación de función, ya que no admiten superíndices. El símbolo de operador más común para la exponenciación es el signo de intercalación (^). La versión original de ASCII incluía un símbolo de flecha hacia arriba (↑), destinado a la exponenciación, pero fue reemplazado por el signo de intercalación en 1967, por lo que el signo de intercalación se volvió habitual en los lenguajes de programación.
Las notaciones incluyen:
x ^ y: AWK, BASIC, J, MATLAB, Wolfram Language (Mathematica), R, Microsoft Excel, Analytica, TeX (y sus derivados), TI-BASIC, bc (para exponentes enteros), Haskell (para exponentes enteros no negativos), Lua y la mayoría de los sistemas de álgebra computarizada.x ** y. El conjunto de caracteres de Fortran no incluía caracteres de minúsculas o símbolos de puntuación distintos+-*/()&=.,'y tan utilizados**para la exposición (la versión inicial utilizadaa xx ben su lugar.). Muchos otros idiomas siguieron el traje: Ada, Z shell, KornShell, Bash, COBOL, CoffeeScript, Fortran, FoxPro, Gnuplot, Groovy, JavaScript, OCaml, F#, Perl, PHP, PL/I, Python, Rexx, Ruby, SAS, Seed7, Tcl, ABAP, Mercury, Haskell (para exponentes de puntos flotantes), Turing, VHDL.x ↑ y: Algol Lenguaje de referencia, Commodore BASIC, TRS-80 Nivel II/III BASIC.x ^^ y: Haskell (para base fraccional, exponentes enteros), D.x⋆y- APL.
En la mayoría de los lenguajes de programación con un operador de exponenciación infijo, es asociativo por la derecha, es decir, a^b^c se interpreta como a^(b^c). Esto se debe a que (a^b)^c es igual a a^(b*c) y, por lo tanto, no es tan útil. En algunos idiomas, es asociativo a la izquierda, especialmente en Algol, Matlab y el lenguaje de fórmulas de Microsoft Excel.
Otros lenguajes de programación usan notación funcional:
(expt x y)- Lisp común.pown x y: F# (para base entero, exponente entero).
Otros solo proporcionan exponenciación como parte de las bibliotecas estándar:
pow(x, y): C, C++mathbiblioteca).Math.Pow(x, y)- C#.math:pow(X, Y)Erlang.Math.pow(x, y)Java.[Math]::Pow(x, y)- PowerShell.
Contenido relacionado
Googolplex
Estereorradián
Notación polaca inversa





![{displaystyle {begin{aligned}b^{n+m}&=underbrace {btimes dots times b} _{n+m{text{ times}}}\[1ex]&=underbrace {btimes dots times b} _{n{text{ times}}}times underbrace {btimes dots times b} _{m{text{ times}}}\[1ex]&=b^{n}times b^{m}end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/1b3910691105e0b2f80e2656b6dc0037980fea92)















































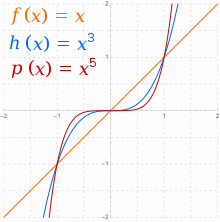















![{displaystyle {sqrt[{n}]{x}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/7b3ba2638d05cd9ed8dafae7e34986399e48ea99)















![{displaystyle left[b^{3},b^{4}right],left[b^{3.1},b^{3.2}right],left[b^{3.14},b^{3.15}right],left[b^{3.141},b^{3.142}right],left[b^{3.1415},b^{3.1416}right],left[b^{3.14159},b^{3.14160}right],ldots }](https://wikimedia.org/api/rest_v1/media/math/render/svg/f09aec126692a109ddd2b003c78002512678e923)


































![{displaystyle left(rho e^{itheta }right)^{frac {1}{n}}={sqrt[{n}]{rho }},e^{frac {itheta }{n}}.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/1fc4ae73419a2cabb0133293dc1bfa19d743b1d9)





































































































![{displaystyle k[x_{1},ldotsx_{n}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/37c2b680cd4b215ac5c3c548a0e596d534526cab)




































































