Exploración de graham

format_list_bulleted Contenido keyboard_arrow_down

ImprimirCitar

Algoritmo para calcular cascos convexos en un conjunto de puntos

Una demostración del escaneo de Graham para encontrar un casco convexo 2D.

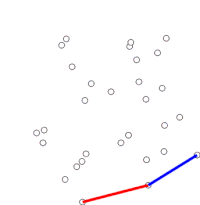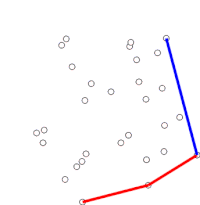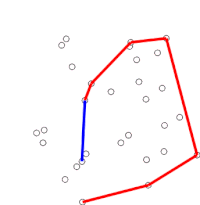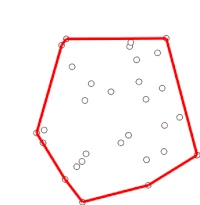
El escaneo de Graham es un método para encontrar el casco convexo de un conjunto finito de puntos en el plano con complejidad temporal O(n log n). Lleva el nombre de Ronald Graham, quien publicó el algoritmo original en 1972. El algoritmo encuentra todos los vértices del casco convexo ordenados a lo largo de su límite. Utiliza una pila para detectar y eliminar concavidades en el límite de manera eficiente.

Algoritmo

El primer paso de este algoritmo es encontrar el punto con la coordenada y más baja. Si la coordenada y más baja existe en más de un punto del conjunto, se debe elegir el punto con la coordenada x más baja entre los candidatos. Llame a este punto P. Este paso requiere O(n), donde n es el número de puntos en cuestión.

A continuación, se debe ordenar el conjunto de puntos en orden creciente del ángulo que forman y el punto P con el eje x. Cualquier algoritmo de clasificación de propósito general es apropiado para esto, por ejemplo heapsort (que es O(n log n)).

La clasificación en orden de ángulo no requiere calcular el ángulo. Es posible utilizar cualquier función del ángulo que es monotónico en el intervalo $[0,pi]$ . El cosine se computa fácilmente utilizando el producto de puntos, o la pendiente de la línea se puede utilizar. Si la precisión numérica está en juego, la función de comparación utilizada por el algoritmo de clasificación puede utilizar el signo del producto de la cruz para determinar ángulos relativos.

Si varios puntos tienen el mismo ángulo, rompa los vínculos aumentando la distancia (se puede usar la distancia de Manhattan o Chebyshev en lugar de la euclidiana para facilitar el cálculo, ya que los puntos se encuentran en el mismo rayo), o elimine todos los puntos excepto el más lejano..

El algoritmo procede considerando cada uno de los puntos de la matriz ordenada en secuencia. Para cada punto, primero se determina si viajar desde los dos puntos inmediatamente anteriores a este punto constituye un giro a la izquierda o a la derecha. Si se gira a la derecha, el penúltimo punto no forma parte del casco convexo y se encuentra "dentro" del casco. él. Luego se hace la misma determinación para el conjunto del último punto y los dos puntos que preceden inmediatamente al punto que se encuentra dentro del casco, y se repite hasta que se produce un "giro a la izquierda" se encuentra el conjunto, momento en el cual el algoritmo pasa al siguiente punto del conjunto de puntos en la matriz ordenada menos cualquier punto que se encuentre dentro del casco; No es necesario volver a considerar estos puntos. (Si en algún momento los tres puntos son colineales, se puede optar por descartarlo o informarlo, ya que en algunas aplicaciones es necesario encontrar todos los puntos en el límite del casco convexo).

Una vez más, determinar si tres puntos constituyen un "volver izquierdo" o un "volver derecho" no requiere calcular el ángulo real entre los segmentos de dos líneas, y en realidad se puede lograr con aritmética simple solamente. Por tres puntos $P_{1}=(x_{1},y_{1})$ , $P_{2}=(x_{2},y_{2})$ y $P_{3}=(x_{3},y_{3})$ , computar el z-coordinado del producto de la cruz de los dos vectores $overrightarrow {P_{1}P_{2}}$ y $overrightarrow {P_{1}P_{3}}$ , que es dada por la expresión $(x_{2}-x_{1})(y_{3}-y_{1})-(y_{2}-y_{1})(x_{3}-x_{1})$ . Si el resultado es 0, los puntos son collinear; si es positivo, los tres puntos constituyen una orientación "izquierda" o en sentido contrario, de lo contrario una "volver derecho" o una orientación en sentido de reloj (para puntos contados).

Este proceso eventualmente regresará al punto en el que comenzó, momento en el cual se completa el algoritmo y la pila ahora contiene los puntos en el casco convexo en orden antihorario.

Complejidad del tiempo

Clasificación de los puntos tiene la complejidad del tiempo O(n log n). Aunque puede parecer que la complejidad del tiempo del bucle es O(n²), porque para cada punto se vuelve a comprobar si cualquiera de los puntos anteriores hacen un " giro derecho", es en realidad O(n), porque cada punto se considera al máximo dos veces en algún sentido. Cada punto puede aparecer sólo una vez como punto $(x_{2},y_{2})$ en un "izquierda vuelta" (porque el algoritmo avanza al siguiente punto $(x_3,y_3)$ después de eso), y como punto $(x_{2},y_{2})$ en un "giro directo" (porque el punto) $(x_{2},y_{2})$ se retira). Por lo tanto, la complejidad general del tiempo es O(n log n), desde el momento de ordenar domina el tiempo para calcular el casco convexo.

Pseudocódigo

El pseudocódigo siguiente utiliza una función ccw: ccw > 0 si tres puntos giran en sentido contrario a las agujas del reloj, en el sentido de las agujas del reloj si ccw < 0, y colineal si ccw = 0. (En aplicaciones reales, si las coordenadas son números reales arbitrarios, la función requiere una comparación exacta de números de punto flotante, y hay que tener cuidado con las singularidades numéricas para "casi" puntos colineales.)

Luego deje que el resultado se almacene en la pila.

Deja puntos Ser la lista de puntos
Deja pila = vacío_stack()

encontrar el punto más bajo y-coordinado e izquierdo, llamado P0
especie puntos por ángulo polar con P0, si varios puntos tienen el mismo ángulo polar entonces sólo mantener el más lejano

para punto dentro puntos:
# pop the last point from the stack if we turn clockwise to reach this point
 mientras Cuenta pila 1 y ccw(next_to_top(stack), top(stack), punto)
 pop pila
 empujar punto a pila
final

Ahora la pila contiene el casco convexo, donde los puntos están orientados en sentido antihorario y P0 es el primer punto.

Aquí, next_to_top() es una función para devolver el elemento una entrada debajo de la parte superior de la pila, sin cambiar la pila, y de manera similar, top() para devolver el elemento más alto.

Este pseudocódigo está adaptado de Introducción a los algoritmos.

Robustez numérica

La robustez numérica es un problema que hay que abordar en los algoritmos que utilizan aritmética informática de punto flotante de precisión finita. Un artículo de 2004 analizó una estrategia incremental simple, que puede usarse, en particular, para una implementación del escaneo de Graham. El objetivo declarado del artículo no era analizar específicamente el algoritmo, sino más bien proporcionar un ejemplo de libro de texto de qué y cómo puede fallar debido a los cálculos de punto flotante en geometría computacional. Más tarde, D. Jiang y N. F. Stewart profundizaron en esto y, utilizando el análisis de errores hacia atrás, llegaron a dos conclusiones principales. La primera es que el casco convexo es un problema bien condicionado y, por tanto, se pueden esperar algoritmos que produzcan una respuesta dentro de un margen de error razonable. En segundo lugar, demuestran que una modificación del escaneo de Graham a la que llaman Graham-Fortune (que incorpora ideas de Steven Fortune para la estabilidad numérica) supera los problemas de precisión finita y datos inexactos "en cualquier medida que sea posible hacerlo". 34;.

Contenido relacionado

Más resultados...