Experimento de Trouton-Noble

Un condensador circular B, 7.7 cm de diámetro, construido a partir de múltiples capas de mica y tinfoil, fue montado en una bola esférica celuloide suave D que estaba cubierto con pintura conductiva, y que fue suspendida por un fino alambre fosfor-bronze de 37 cm de largo dentro de un tubo de tierra. El alambre estaba conectado a un electrodo de una máquina Wimshurst que mantenía placas alternas del condensador cargadas a 3000 voltios. Las placas opuestas del condensador, así como la bola celuloide, fueron mantenidas a tensión terrestre por medio de un alambre de platino que cayó en un baño de ácido sulfúrico que no sólo sirvió como electrodo conductivo, sino también oscilaciones amortiguadas y actuó como un desiccánt. Un espejo unido al condensador fue visto a través de un telescopio y permitió que se vieran cambios finos en la orientación.

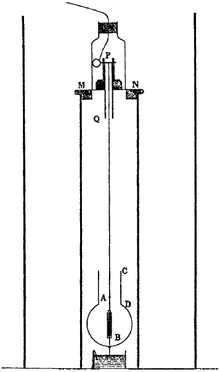
El experimento de Trouton-Noble fue un intento de detectar el movimiento de la Tierra a través del éter luminífero y fue realizado entre 1901 y 1903 por Frederick Thomas Trouton y H. R. Noble. Se basó en una sugerencia de George FitzGerald de que un capacitor de placas paralelas cargadas que se mueve a través del éter debería orientarse perpendicularmente al movimiento. Al igual que el experimento anterior de Michelson-Morley, Trouton y Noble obtuvieron un resultado nulo: no se pudo detectar ningún movimiento relativo al éter. Este resultado nulo fue reproducido, con sensibilidad creciente, por Rudolf Tomaschek (1925, 1926), Chase (1926, 1927) y Hayden en 1994. Ahora se considera que tales resultados experimentales, de acuerdo con la relatividad especial, reflejan la validez del principio de la relatividad y la ausencia de cualquier marco de reposo absoluto (o éter). El experimento es una prueba de la relatividad especial.

El experimento de Trouton-Noble también está relacionado con experimentos mentales como la "paradoja de Trouton-Noble" y la "palanca de ángulo recto" o la "paradoja de Lewis-Tolman". Se han propuesto varias soluciones para resolver este tipo de paradojas, todas ellas de acuerdo con la relatividad especial.

Experimento Trouton-Noble

En el experimento, un capacitor suspendido de placas paralelas está sujeto por una fina fibra de torsión y está cargado. Si la teoría del éter fuera correcta, el cambio en las ecuaciones de Maxwell debido al movimiento de la Tierra a través del éter daría lugar a un par que haría que las placas se alinearan perpendiculares al movimiento. Esto viene dado por:

τ τ =− − E.v2c2pecado⁡ ⁡ 2α α .{displaystyle tau =-E'{frac {V^{2} {c^{2}}sin 2alpha}

Donde τ τ {displaystyle tau } es el par, E{displaystyle E} la energía del condensador, α α {displaystyle alpha } el ángulo entre la normalidad de la placa y la velocidad.

Por otro lado, la afirmación de la relatividad especial de que las ecuaciones de Maxwell son invariantes para todos los marcos de referencia que se mueven a velocidades constantes no predeciría ningún par (un resultado nulo). Por lo tanto, a menos que el éter estuviera de alguna manera fijo en relación con la Tierra, el experimento es una prueba de cuál de estas dos descripciones es más precisa. Su resultado nulo confirma así la invariancia de Lorentz de la relatividad especial.

Sin embargo, mientras que el resultado experimental negativo se puede explicar fácilmente en el marco de reposo del dispositivo, la explicación desde el punto de vista de un marco que no se mueve (con respecto a la pregunta, si debe surgir el mismo par que en el & #34;estructura de éter" descrita anteriormente, o si no surge ningún par) es mucho más difícil y se denomina "paradoja de Trouton-Noble," que se puede resolver de varias maneras (ver Soluciones a continuación).

Paradoja de la palanca de ángulo recto

La paradoja Trouton-Noble es esencialmente equivalente a un experimento de pensamiento llamado el paradoja de palanca ángulo recto, primero discutido por Gilbert Newton Lewis y Richard Chase Tolman en 1909. Suponga una palanca de ángulo derecho con puntos finales abc. En su marco de descanso, las fuerzas fSí.{displaystyle f_{y} hacia ba y fx{displaystyle f_{x} hacia bc debe ser igual a obtener equilibrio, por lo que ninguna torque es dada por la ley de la palanca:

τ τ .=L0()fx.− − fSí..)=0{displaystyle tau '=L_{0}left(f'_{x}-f'_{y}right)=0}

Donde τ τ {displaystyle tau } es el par, y L0{displaystyle L_{0} la longitud del resto de un brazo de palanca. Sin embargo, debido a la contracción de longitud, ba es más largo que bc en un sistema de no movimiento, por lo tanto la ley de la palanca da:

τ τ =fx⋅ ⋅ L0− − fSí.⋅ ⋅ L01− − v2c2=L0()fx− − fSí.1− − v2c2){displaystyle tau =f_{x}cdot L_{0}-f_{y}cdot L_{0}{sqrt {1-{frac {f} {f} {f}} {f} {f} {f}} {f}}} {f}}} {f}}}} {f} {f}} {f}} {f}}} {f}}} {f}}}}} {f}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}} {m}} {m_}} {m_} {m_}}}}}}}}}}}}}}}}}}}}}}}}}}}} {m_}}} {m_}}}} {m_}} {m_}}} {m_}}}}}}} {m_}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}} {1-{frac {fnMicrosoft Sans Serif}

Se puede ver que el par de torsión no es cero, lo que aparentemente haría que la palanca girara en el marco sin movimiento conjunto. Dado que no se observa rotación, Lewis y Tolman concluyeron que no existe torque, por lo tanto:

fxfSí.=1− − v2c2{displaystyle {frac {f}{f_{y}={sqrt {1-{frac {c}}}}} {c}}} {c}}} {c}}}} {c}}}}}}}}}}}}}} {c} {c}}}}}} {c}}}}} {c}}}}}}}} {c}}}}}}}}}}} {}}}}}}}}}}}}}}}}}}}}}} {}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}} {}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}

Sin embargo, como muestra Max von Laue (1911), esto está en contradicción con las expresiones relativistas de fuerza,

fx=fx.,fSí.=fSí..⋅ ⋅ 1− − v2c2{displaystyle f_{x}=f'_{x}, ¿Qué? {f}}}

que da

fxfSí.=11− − v2c2{displaystyle {frac {f}{f_{y}}={frac} {f}} {f}} {f}}}}}} {f} {f}}} {f}}} {f}}} {2}}}}

Cuando se aplica la ley de la palanca, se produce el siguiente par:

τ τ =− − L0⋅ ⋅ fx.⋅ ⋅ v2c2{displaystyle tau ¿Qué?

Que es principalmente el mismo problema que en la paradoja de Trouton-Noble.

Soluciones

El análisis relativista detallado tanto de la paradoja de Trouton-Noble como de la paradoja de la palanca del ángulo recto requiere cuidado para conciliar correctamente, por ejemplo, los efectos vistos por los observadores en diferentes marcos de referencia, pero en última instancia, se demuestra que todas esas descripciones teóricas dar el mismo resultado. En ambos casos, un momento de torsión neto aparente en un objeto (cuando se ve desde un cierto marco de referencia) no da como resultado ninguna rotación del objeto, y en ambos casos esto se explica contabilizando correctamente, de forma relativista, la transformación de todas las fuerzas relevantes, los momentos y las aceleraciones producidas por ellos. Janssen (1995) revisa la historia temprana de las descripciones de este experimento.

Corriente de Laue

La primera solución de la paradoja de Trouton-Noble fue dada por Hendrik Lorentz (1904). Su resultado se basa en la suposición de que el par y el momento debidos a las fuerzas electrostáticas se compensan con el par y el momento debidos a las fuerzas moleculares. Sin embargo, no existe un mecanismo conocido de cómo una transformación de Lorentz podría producir tales fuerzas moleculares. Además, si dos cargas puntuales están conectadas por una cuerda flexible, ninguna fuerza molecular podría producir un momento de giro.

Esto fue más elaborado por Max von Laue (1911), quien dio la solución estándar para este tipo de paradojas. Se basaba en la llamada "inercia de la energía" en su formulación general por Max Planck. Según Laue, en los cuerpos en movimiento se produce una corriente de energía conectada con un cierto momento ('corriente de Laue') por esfuerzos elásticos. El par mecánico resultante en el caso del experimento de Trouton-Noble asciende a:

τ τ =E.v2c2pecado⁡ ⁡ 2α α .{displaystyle tau =E'{frac {V^{2} {c^{2}}sin 2alpha}

y en la palanca de ángulo derecho:

τ τ =L0⋅ ⋅ fx.⋅ ⋅ v2c2{displaystyle tau =L_{0}cdot f'_{x}cdot {frac {f}{c^{2}}}}} {c}}}} {cdot {cdot {f}}} {c}}}}}}} {cdot}}}} {cdot}}}}}}}}}}}}}}} {

que compensa exactamente el par electromagnético mencionado anteriormente, por lo que no se produce rotación en ambos casos. O en otras palabras: el par electromagnético es realmente necesario para el movimiento uniforme de un cuerpo, es decir, para impedir que el cuerpo gire debido al par mecánico causado por las tensiones elásticas.

Desde entonces, aparecieron muchos artículos que profundizaban en la corriente de Laue, proporcionando algunas modificaciones o reinterpretaciones, e incluían diferentes variantes de "oculto" impulso.

Fuerza y aceleración

Richard C. Tolman y Paul Sophus Epstein publicaron una solución sin fuerzas compensatorias ni redefiniciones de fuerza y equilibrio en 1911. Aplicaron la noción de una masa relativista que era diferente en la dirección longitudinal y en la dirección transversal, de modo que la fuerza y la aceleración no siempre tienen la misma dirección. El papel que juega el concepto de fuerza en la relatividad es muy diferente al de la mecánica newtoniana. A una conclusión similar llegó Franklin (2006), usando una masa invariable que no cambiaba con la dirección, pero usando el hecho de que la dirección de la aceleración relativista es diferente de la dirección de la fuerza relativista.

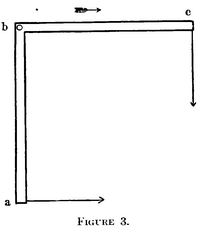
Epstein imaginaba una varilla sin masa con endpoints OM, que se monta en el punto O, y una partícula con masa de descanso m se monta en M (ver [1]). La barra forma el ángulo #⁡ ⁡ α α .{displaystyle tan alpha ' con el eje y. Ahora una fuerza f.{displaystyle f'} hacia O se aplica en M, y equilibrio en su marco de descanso se consigue cuando fx.fSí..=#⁡ ⁡ α α .{displaystyle {tfrac {f}{f'}}=tan alpha '}. Como ya se ha demostrado anteriormente, estas fuerzas tienen la forma en un marco de no movimiento:

fx=fx.,fSí.=fSí..⋅ ⋅ 1− − v2c2,#⁡ ⁡ α α =#⁡ ⁡ α α .1− − v2c2{displaystyle f_{x}=f'_{x}, ¿Qué? {sqrt {1-{2}}}} tan alpha = tan alpha '{sqrt {1-{frac {c}}}}} {c}}} {c}}} {c}}}} {c}}}}}}}}}}}}}} {c} {c}}}}}} {c}}}}} {c}}}}}}}} {c}}}}}}}}}}} {}}}}}}}}}}}}}}}}}}}}}} {}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}} {}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}

Así fxfSí.=#⁡ ⁡ α α 1− − v2c2{displaystyle {frac {f}{f_{y}}={frac} {f}} {f}} {f}}}}}} {f} {f}}} {f}}} {f}}} {tan alpha }{1-{frac {c}}}}} {c}}} {c}}} {c}}}} {c}}}}}}}}}}}}}} {c} {c}}}}}} {c}}}}} {c}}}}}}}} {c}}}}}}}}}}} {}}}}}}}}}}}}}}}}}}}}}} {}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}} {}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}.

Entonces, la fuerza resultante no apunta directamente de O a M. ¿Conduce esto a una rotación de la varilla? No, porque Epstein ahora consideró las aceleraciones causadas por las dos fuerzas. Usó el concepto de una masa relativista que era diferente en la dirección longitudinal y la dirección transversal tal que

mlong.=m0γ γ 3,mtr.=m0γ γ ,whereγ γ =11− − v2c2{displaystyle m_{rm}={m_{0}gamma ^{3}, m_{rm {}=m_{0}gammaquad {rm}quad gamma ={frac} {1}{sqrt {1-{frac} {c}}}}} {c}}} {c}}}}}} {c}}}}}} {c}}}}}}}}}}}}}}}}}}}}} {c}}}}}}}}}}}}}}}}}}}}}}} {c}}}} {}}}}}}}}}}}}}}}} {}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}} {}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}.

Las expresiones relativistas en el caso en que una masa m es acelerada por estas dos fuerzas en dirección longitudinal y transversal, son

ax=fxmγ γ 3,aSí.=fSí.mγ γ {displaystyle a_{x}={f_{x}{mgamma ^{3}} a_{y}={frac {f}{mgamma }.

Así axaSí.=#⁡ ⁡ α α {fnMicroc} Tan alpha.

Franklin usó la conexión relativista entre fuerza y aceleración,

dpdt=mddt()vγ γ )=mγ γ 3[a+v× × ()v× × a)].{fnMicroc {bf} {}} {bf {bf}gamma)=mgamma ^{3}[{bf {bf {bf {bf {bf {bf {f {cH00times (vtimes a)}}}}}}}} {f}}}}} {f}}}}}}}}}} {p}}}}}}}}} {f}}}}}}} {bf}}}}}}}} {bh}}}}}} {bf}}} {bf}}}}}}}}}}}}}}}}} {bf}}} {bf} {bf}}} {bf} {bf}}}}} {bh}}}}}}}}}}}}}}}}}}}}}} {bf}}}}}}}}}}}}}}}}}}}}} {

Usando esta relación entre la fuerza relativista y la aceleración, se puede demostrar que no se produce rotación en este sistema. También se deben aplicar consideraciones similares a la palanca de ángulo recto y la paradoja de Trouton-Noble. Así se resuelven las paradojas, porque las dos aceleraciones (como vectores) apuntan al centro de gravedad del sistema, aunque las dos fuerzas no.