Experimento de Franck-Hertz

El experimento de Franck-Hertz fue la primera medición eléctrica que mostró claramente la naturaleza cuántica de los átomos y, por lo tanto, "transformó nuestra comprensión del mundo". Fue presentado el 24 de abril de 1914 a la Sociedad Alemana de Física en un artículo de James Franck y Gustav Hertz. Franck y Hertz habían diseñado un tubo de vacío para estudiar electrones energéticos que volaban a través de un fino vapor de átomos de mercurio. Descubrieron que, cuando un electrón chocaba con un átomo de mercurio, sólo podía perder una cantidad específica (4,9 electronvoltios) de su energía cinética antes de volar. Esta pérdida de energía corresponde a desacelerar el electrón desde una velocidad de aproximadamente 1,3 millones de metros por segundo hasta cero. Un electrón más rápido no desacelera completamente después de una colisión, sino que pierde exactamente la misma cantidad de su energía cinética. Los electrones más lentos simplemente rebotan en los átomos de mercurio sin perder ninguna velocidad o energía cinética significativa.

Estos resultados experimentales demostraron ser consistentes con el modelo de Bohr para átomos que había sido propuesto el año anterior por Niels Bohr. El modelo de Bohr fue un precursor de la mecánica cuántica y del modelo atómico de la capa electrónica. Su característica clave era que un electrón dentro de un átomo ocupa uno de los "niveles de energía cuántica" del átomo. Antes de la colisión, un electrón dentro del átomo de mercurio ocupa su nivel de energía más bajo disponible. Después de la colisión, el electrón del interior ocupa un nivel de energía más alto con 4,9 electronvoltios (eV) más de energía. Esto significa que el electrón está más débilmente unido al átomo de mercurio. No había niveles ni posibilidades intermedias en el modelo cuántico de Bohr. Esta característica fue "revolucionaria" porque era inconsistente con la expectativa de que un electrón pudiera unirse al núcleo de un átomo mediante cualquier cantidad de energía.

En un segundo artículo presentado en mayo de 1914, Franck y Hertz informaron sobre la emisión de luz por los átomos de mercurio que habían absorbido energía de las colisiones. Demostraron que la longitud de onda de esta luz ultravioleta correspondía exactamente a los 4,9 eV de energía que había perdido el electrón volador. Bohr también había predicho la relación entre energía y longitud de onda porque había seguido la estructura establecida por Hendrik Lorentz en el Congreso Solvay de 1911. En Solvay, Hendrik Lorentz sugirió, después de la charla de Einstein sobre la estructura cuántica, que la energía de un rotador se igualara a nhv. Por lo tanto, Bohr siguió las instrucciones dadas en 1911 y copió la fórmula propuesta por Lorentz y otros en su modelo atómico de 1913. Lorentz había estado en lo cierto. La cuantificación de los átomos coincidía con su fórmula incorporada al modelo de Bohr. Después de que Franck presentara estos resultados unos años más tarde, se dice que Albert Einstein comentó: "Es tan hermoso que te hace llorar".

On December 10, 1926, Franck and Hertz were awarded the 1925 Nobel Prize in Physics "for their discovery of the laws governing the impact of an electron upon an atom#34;.

Experimento

El experimento original de Franck y Hertz utilizó un tubo de vacío calentado que contenía una gota de mercurio; informaron de una temperatura del tubo de 115 °C, a la que la presión de vapor del mercurio es de unos 100 pascales (y muy por debajo de la presión atmosférica). En la fotografía se muestra un tubo Franck-Hertz contemporáneo. Está equipado con tres electrodos: un cátodo caliente que emite electrones; una rejilla de malla metálica; y un ánodo. El voltaje de la rejilla es positivo en relación con el cátodo, de modo que los electrones emitidos por el cátodo caliente son atraídos hacia él. La corriente eléctrica medida en el experimento se debe a los electrones que atraviesan la rejilla y llegan al ánodo. El potencial eléctrico del ánodo es ligeramente negativo en relación con la rejilla, de modo que los electrones que llegan al ánodo tienen al menos una cantidad correspondiente de energía cinética después de pasar la rejilla.

Los gráficos publicados por Franck y Hertz (ver figura) muestran la dependencia de la corriente eléctrica que sale del ánodo del potencial eléctrico entre la rejilla y el cátodo.

• En las diferencias de bajo potencial —hasta 4.9 voltios— la corriente a través del tubo aumentó constantemente con creciente diferencia potencial. Este comportamiento es típico de verdaderos tubos de vacío que no contienen vapor de mercurio; voltajes más grandes conducen a una mayor "actualización limitada de carga espacial".
• A 4.9 voltios las caídas actuales agudamente, casi de vuelta a cero.
• La corriente entonces aumenta constantemente una vez más a medida que el voltaje se aumenta más, hasta alcanzar 9.8 voltios (exactamente 4.9+4.9 voltios).
• A las 9.8 voltios se observa una gota afilada similar.
• Aunque no es evidente en las mediciones originales de la figura, esta serie de saltos en corriente a unos incrementos de 4,9 voltios continúa hasta potenciales de al menos 70 voltios.

Franck y Hertz observaron en su primer artículo que la energía característica de 4,9 eV de su experimento correspondía bien a una de las longitudes de onda de la luz emitida por los átomos de mercurio en las descargas de gas. Utilizaban una relación cuántica entre la energía de excitación y la correspondiente longitud de onda de la luz, que en términos generales atribuían a Johannes Stark y Arnold Sommerfeld; predice que 4,9 eV corresponden a luz con una longitud de onda de 254 nm. La misma relación también se incorporó en la teoría fotónica del efecto fotoeléctrico de Einstein de 1905. En un segundo artículo, Franck y Hertz informaron sobre la emisión óptica de sus tubos, que emitían luz con una única longitud de onda prominente de 254 nm. La figura de la derecha muestra el espectro de un tubo de Franck-Hertz; Casi toda la luz emitida tiene una única longitud de onda. Como referencia, la figura también muestra el espectro de una luz de descarga de gas mercurio, que emite luz en varias longitudes de onda además de 254 nm. La cifra se basa en los espectros originales publicados por Franck y Hertz en 1914. El hecho de que el tubo de Franck-Hertz emitiera solo una única longitud de onda, correspondiente casi exactamente al período de voltaje que habían medido, fue muy importante.

Modelado de colisiones de electrones con átomos

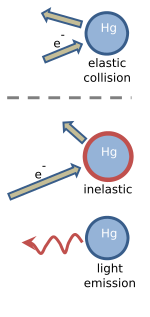
Franck y Hertz explicaron su experimento en términos de colisiones elásticas e inelásticas entre los electrones y los átomos de mercurio. Los electrones que se mueven lentamente chocan elásticamente con los átomos de mercurio. Esto significa que la dirección en la que se mueve el electrón se ve alterada por la colisión, pero su velocidad no cambia. En la figura se ilustra una colisión elástica, donde la longitud de la flecha indica la velocidad del electrón. El átomo de mercurio no se ve afectado por la colisión, principalmente porque es unas cuatrocientas mil veces más masivo que un electrón.

Cuando la velocidad del electrón excede aproximadamente 1,3 millones de metros por segundo, las colisiones con un átomo de mercurio se vuelven inelásticas. Esta velocidad corresponde a una energía cinética de 4,9 eV, que se deposita en el átomo de mercurio. Como se muestra en la figura, la velocidad del electrón se reduce y el átomo de mercurio se "excita". Poco tiempo después, los 4,9 eV de energía que se depositaron en el átomo de mercurio se liberan en forma de luz ultravioleta que tiene una longitud de onda de exactamente 254 nm. Tras la emisión de luz, el átomo de mercurio vuelve a su estado original, no excitado.

Si los electrones emitidos por el cátodo volaran libremente hasta llegar a la red, adquirirían una energía cinética proporcional al voltaje aplicado a la red. 1 eV de energía cinética corresponde a una diferencia de potencial de 1 voltio entre la red y el cátodo. Las colisiones elásticas con los átomos de mercurio aumentan el tiempo que tarda un electrón en llegar a la red, pero la energía cinética promedio de los electrones que llegan allí no se ve muy afectada.

Cuando el voltaje de la red alcanza los 4,9 V, las colisiones de electrones cerca de la red se vuelven inelásticas y los electrones se ralentizan considerablemente. La energía cinética de un electrón típico que llega a la rejilla se reduce tanto que no puede viajar más para llegar al ánodo, cuyo voltaje está configurado para repeler ligeramente los electrones. La corriente de electrones que llega al ánodo disminuye, como se ve en el gráfico. Nuevos aumentos en el voltaje de la red devuelven suficiente energía a los electrones que sufrieron colisiones inelásticas para que puedan alcanzar nuevamente el ánodo. La corriente vuelve a aumentar cuando el potencial de la red supera los 4,9 V. A 9,8 V la situación vuelve a cambiar. Los electrones que han recorrido aproximadamente la mitad del camino desde el cátodo hasta la red ya han adquirido suficiente energía para sufrir una primera colisión inelástica. A medida que continúan lentamente hacia la red desde el punto medio, su energía cinética se acumula nuevamente, pero cuando llegan a la red pueden sufrir una segunda colisión inelástica. Una vez más, la corriente hacia el ánodo cae. A intervalos de 4,9 voltios se repetirá este proceso; cada vez los electrones sufrirán una colisión inelástica adicional.

Teoría cuántica temprana

Si bien Franck y Hertz no lo sabían cuando publicaron sus experimentos en 1914, en 1913 Niels Bohr había publicado un modelo para los átomos que tuvo mucho éxito al explicar las propiedades ópticas del hidrógeno atómico. Generalmente se observaban en descargas de gas, que emitían luz en una serie de longitudes de onda. Las fuentes de luz ordinarias, como las bombillas incandescentes, emiten luz en todas las longitudes de onda. Bohr había calculado con mucha precisión las longitudes de onda emitidas por el hidrógeno.

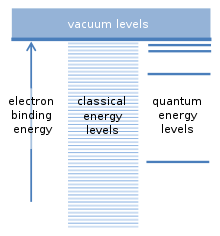
El supuesto fundamental del modelo de Bohr se refiere a las posibles energías de unión de un electrón al núcleo de un átomo. El átomo puede ionizarse si una colisión con otra partícula proporciona al menos esta energía de enlace. Esto libera el electrón del átomo y deja atrás un ion cargado positivamente. Existe una analogía con los satélites que orbitan alrededor de la Tierra. Cada satélite tiene su propia órbita y prácticamente cualquier distancia orbital y cualquier energía de enlace del satélite es posible. Dado que un electrón es atraído por la carga positiva del núcleo atómico mediante una fuerza similar, la llamada fuerza "clásica" Los cálculos sugieren que cualquier energía de enlace también debería ser posible para los electrones. Sin embargo, Bohr supuso que sólo se produce una serie específica de energías de enlace, que corresponden a los "niveles de energía cuántica" para el electrón. Un electrón normalmente se encuentra en el nivel de energía más bajo, con la mayor energía de enlace. Los niveles adicionales se encuentran más arriba, con energías de enlace más pequeñas. No se permiten energías vinculantes intermedias que se encuentren entre estos niveles. Esta fue una suposición revolucionaria.

Franck y Hertz habían propuesto que la característica de 4,9 V de sus experimentos se debía a la ionización de los átomos de mercurio por colisiones con los electrones voladores emitidos en el cátodo. En 1915, Bohr publicó un artículo en el que señalaba que las mediciones de Franck y Hertz eran más consistentes con la suposición de niveles cuánticos en su propio modelo para los átomos. En el modelo de Bohr, la colisión excitó un electrón interno dentro del átomo desde su nivel más bajo hasta el primer nivel cuántico por encima de él. El modelo de Bohr también predijo que la luz se emitiría cuando el electrón interno regresara de su nivel cuántico excitado al más bajo; su longitud de onda correspondía a la diferencia de energía de los niveles internos del átomo, lo que se ha denominado relación de Bohr. La observación de Franck y Hertz de la emisión de su tubo a 254 nm también fue consistente con la perspectiva de Bohr. En sus escritos posteriores al final de la Primera Guerra Mundial en 1918, Franck y Hertz habían adoptado en gran medida la perspectiva de Bohr para interpretar su experimento, que se ha convertido en uno de los pilares experimentales de la mecánica cuántica. Como lo describió Abraham Pais, "Ahora bien, la belleza del trabajo de Franck y Hertz no reside sólo en la medición de la pérdida de energía E₂-E₁ del electrón incidente, pero también observaron que, cuando la energía de ese electrón supera los 4,9 eV, el mercurio comienza a emitir luz ultravioleta de una frecuencia definida ν. como se define en la fórmula anterior. ¡De este modo dieron (al principio sin saberlo) la primera prueba experimental directa de la relación de Bohr!" El propio Franck enfatizó la importancia del experimento de emisión ultravioleta en un epílogo de la película del Comité de Estudio de Ciencias Físicas (PSSC) de 1960 sobre el experimento de Franck-Hertz.

Experimenta con neón

En los laboratorios de instrucción, el experimento de Franck-Hertz a menudo se realiza utilizando gas neón, que muestra la aparición de colisiones inelásticas con un brillo naranja visible en el tubo de vacío, y que tampoco es tóxico, en caso de que el tubo se rompa. Con los tubos de mercurio, el modelo de colisiones elásticas e inelásticas predice que debería haber bandas estrechas entre el ánodo y la rejilla donde el mercurio emite luz, pero la luz es ultravioleta e invisible. Con el neón, el intervalo de voltaje Franck-Hertz es de 18,7 voltios y aparece un brillo naranja cerca de la rejilla cuando se aplican 18,7 voltios. Este brillo se acercará al cátodo con un potencial de aceleración creciente e indica los lugares donde los electrones han adquirido los 18,7 eV necesarios para excitar un átomo de neón. A 37,4 voltios serán visibles dos brillos distintos: uno a medio camino entre el cátodo y la rejilla, y otro justo en la rejilla de aceleración. Potenciales más altos, espaciados a intervalos de 18,7 voltios, darán como resultado regiones brillantes adicionales en el tubo.

Una ventaja adicional del neón para laboratorios de instrucción es que el tubo se puede utilizar a temperatura ambiente. Sin embargo, la longitud de onda de la emisión visible es mucho más larga de lo predicho por la relación de Bohr y el intervalo de 18,7 V. Una explicación parcial de la luz naranja implica dos niveles atómicos que se encuentran 16,6 eV y 18,7 eV por encima del nivel más bajo. Los electrones excitados al nivel de 18,7 eV caen al nivel de 16,6 eV, con la emisión concomitante de luz naranja.