Experimento de Fizeau

El experimento de Fizeau fue llevado a cabo por Hippolyte Fizeau en 1851 para medir las velocidades relativas de la luz en el agua en movimiento. Fizeau utilizó un dispositivo especial de interferómetro para medir el efecto del movimiento de un medio sobre la velocidad de la luz.

Según las teorías que prevalecían en la época, la luz que viaja a través de un medio en movimiento sería arrastrada por el medio, de modo que la velocidad medida de la luz sería una simple suma de su velocidad a través del medio más la velocidad del medio. Fizeau detectó efectivamente un efecto de arrastre, pero la magnitud del efecto que observó fue mucho menor de lo esperado. Cuando repitió el experimento con aire en lugar de agua, no observó ningún efecto. Sus resultados aparentemente respaldaron la hipótesis del arrastre parcial del éter de Augustin-Jean Fresnel, una situación que desconcertó a la mayoría de los físicos. Pasó más de medio siglo antes de que se desarrollara una explicación satisfactoria de la inesperada medición de Fizeau con el advenimiento de la teoría de la relatividad especial de Albert Einstein. Einstein señaló más tarde la importancia del experimento para la relatividad especial, en la que corresponde a la fórmula relativista de adición de velocidades cuando se limita a velocidades pequeñas.

Aunque se lo conoce como el experimento de Fizeau, Fizeau fue un experimentador activo que llevó a cabo una amplia variedad de experimentos diferentes que implicaban medir la velocidad de la luz en diversas situaciones.

En el siglo XVIII, cuando los científicos trabajaban en una teoría de la luz y del electromagnetismo, el éter luminífero, un medio que podría soportar las ondas, fue el foco de muchos experimentos. Dos cuestiones críticas eran la relación del éter con el movimiento y su relación con la materia. Por ejemplo, se propuso que la aberración astronómica, el movimiento aparente de las estrellas observado en diferentes épocas del año, estaba relacionada con la luz de las estrellas propagada a través de un éter. En 1846, Fresnel propuso que la parte del éter que se moverá con un objeto se relaciona con el índice de refracción de la luz del objeto, que se consideraba como la relación entre la velocidad de la luz en el material y la velocidad de la luz en el espacio interestelar. Habiendo medido recientemente la velocidad de la luz en el aire y el agua, Fizeau se propuso medir la velocidad de la luz en el agua en movimiento.

En la figura 2 se presenta una representación muy simplificada del experimento de Fizeau de 1851. La luz entrante se divide en dos haces mediante un divisor de haz (BS) y pasa a través de dos columnas de agua que fluyen en direcciones opuestas. Luego, los dos haces se recombinan para formar un patrón de interferencia que puede ser interpretado por un observador.

La disposición simplificada ilustrada en la figura 2 habría requerido el uso de luz monocromática, lo que habría permitido obtener sólo franjas tenues. Debido a la corta longitud de coherencia de la luz blanca, el uso de luz blanca habría requerido adaptar las trayectorias ópticas a un grado de precisión poco práctico, y el aparato habría sido extremadamente sensible a la vibración, los cambios de movimiento y los efectos de la temperatura.

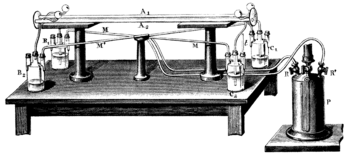
El aparato de Fizeau, ilustrado en las figuras 3 y 4, estaba diseñado como un interferómetro de trayectoria común. Esto garantizaba que los rayos opuestos pasarían por trayectorias equivalentes, de modo que las franjas se formaban fácilmente incluso cuando se utilizaba el sol como fuente de luz.

El doble tránsito de la luz fue con el propósito de aumentar la distancia atravesada en el medio en movimiento, y además compensar por completo cualquier diferencia accidental de temperatura o presión entre los dos tubos, de los cuales podría resultar un desplazamiento de los flecos, que se mezclaría con el desplazamiento que la moción habría producido por sí sola, y por lo tanto han hecho que la observación de ella sea incierta.

—Fizeau

Un rayo de luz que emana de la fuente S′ es reflejado por un divisor de haz G y colimado en un haz paralelo por la lente L. Después de pasar por las rendijas O₁ y O₂, dos rayos de luz viajan a través de los tubos A₁ y A₂, a través de los cuales fluye agua de un lado a otro como lo muestran las flechas. Los rayos se reflejan en un espejo m situado en el foco de la lente L′, de modo que un rayo siempre se propaga en la misma dirección que la corriente de agua y el otro en dirección opuesta a la de la corriente de agua. Después de pasar de un lado a otro a través de los tubos, ambos rayos se unen en S, donde producen franjas de interferencia que pueden visualizarse a través del ocular ilustrado. El patrón de interferencia puede analizarse para determinar la velocidad de la luz que viaja a lo largo de cada pata del tubo.

El experimento de Fizeau demostró que la velocidad de la luz era mayor en el agua que se movía en la misma dirección y menor cuando el agua se movía en sentido contrario a la luz. Sin embargo, la diferencia en la velocidad de la luz era solo una fracción de la velocidad del agua. Interpretado en términos de la teoría del éter, el agua parecía arrastrar el éter y, por lo tanto, la propagación de la luz, pero solo parcialmente.

En la época del experimento de Fizeau, se discutieron dos modelos diferentes de cómo el éter se relacionaba con los cuerpos en movimiento: la hipótesis de arrastre parcial de Fresnel y la hipótesis de arrastre completo del éter de George Stokes. Fresnel hizo que Augustin-Jean Fresnel (1818) propusiera su modelo para explicar un experimento de Arago de 1810. En 1845, Stokes demostró que el arrastre completo del éter también podía explicarlo. Dado que Fresnel no tenía un modelo para explicar el arrastre parcial, los científicos favorecieron la explicación de Stokes.

Según la hipótesis de Stokes, la velocidad de la luz debería aumentar o disminuir cuando es "arrastrada" por el agua a través del marco del éter, dependiendo de la dirección. La velocidad total de un haz de luz debería ser una simple suma aditiva de su velocidad a través del agua más la velocidad del del agua. Es decir, si n es el índice de refracción del agua, de modo que c/n es la velocidad de la luz en agua estacionaria, entonces la velocidad predicha de la luz w en un brazo sería

${\displaystyle w_{+}={\frac {c} {n}+v}$

y la velocidad prevista en el otro brazo sería

${\displaystyle w_{-}={\frac {c} {n}-v}$

para el agua con velocidad ${\displaystyle v}$. Por lo tanto, la luz que viaja contra el flujo de agua debe ser más lenta que la luz que viaja con el flujo de agua. El patrón de interferencia entre las dos vigas cuando la luz es recombinada en el observador depende de los tiempos de tránsito sobre los dos caminos.

Sin embargo, Fizeau descubrió que

${\displaystyle w_{+}={\frac {c}{n}+v\left(1-{\frac} Bien.$

En otras palabras, la luz parecía ser arrastrada por el agua, pero la magnitud del arrastre era mucho menor de lo esperado.

El experimento de Fizeau obligó a los físicos a aceptar la validez empírica de un modelo de Fresnel, según el cual un medio que se mueve a través del éter estacionario arrastra la luz que se propaga a través de él con sólo una fracción de la velocidad del medio, con un coeficiente de arrastre f relacionado con el índice de refracción:

${\displaystyle f=1-{\frac {1}{n^{2}}\$

Aunque la hipótesis de Fresnel resultó empíricamente satisfactoria para explicar los resultados de Fizeau, muchos expertos en la materia, incluido el propio Fizeau, consideraron que la hipótesis de Fresnel sobre el arrastre parcial del éter no era satisfactoria. Fresnel había encontrado una fórmula empírica que funcionaba, pero no se había utilizado ningún modelo mecánico del éter para derivarla.

En 1870, Wilhelm Veltmann demostró que la fórmula de Fresnel funcionaba para distintas frecuencias (colores) de luz. Según el modelo de Fresnel, esto implicaría distintas cantidades de resistencia al avance de la tierra para distintos colores de luz. La velocidad con luz blanca, una mezcla de colores, no tendría explicación.

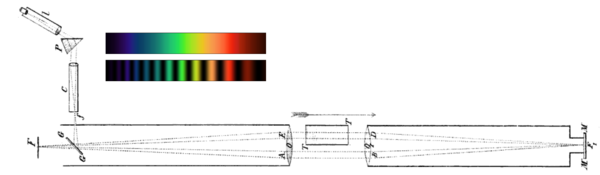
Martin Hoek (1868) proporcionó una confirmación indirecta del coeficiente de arrastre de Fresnel. Su aparato era similar al de Fizeau, aunque en su versión sólo un brazo contenía un área llena de agua en reposo, mientras que el otro brazo estaba en el aire. Como lo ve un observador que descansa en el éter, la Tierra y, por lo tanto, el agua están en movimiento. Por lo tanto, Hoek calculó los siguientes tiempos de viaje de dos rayos de luz que viajan en direcciones opuestas (sin tener en cuenta la dirección transversal, ver imagen):

${\displaystyle {\fnMicroc} {\fnK} {\fnMicroc} {\fnMicroc}} {\fnMicroc} {c} {n}-v}$ ${\displaystyle ## {2}={\frac {AB}{c-v}+{\frac} {DE}{\frac} {c} {n}+v}\.}$

Los tiempos de viaje no son los mismos, lo que debería indicarse mediante un cambio de interferencia. Sin embargo, si se aplica el coeficiente de arrastre de Fresnel al agua en el marco del éter, la diferencia de tiempo de viaje (de primer orden en v/c) desaparece. Al girar la mesa del aparato 180 grados, alterando la dirección de un viento de éter hipotético, Hoek obtuvo un resultado nulo, lo que confirma el coeficiente de arrastre de Fresnel.

En la versión particular del experimento que se muestra aquí, Hoek utilizó un prisma P para dispersar la luz desde una rendija en un espectro que pasaba por un colimador C antes de entrar en el aparato. Con el aparato orientado en paralelo al viento de éter hipotético, Hoek esperaba que la luz en un circuito se retrasara 7/600 mm con respecto al otro. Cuando este retraso representaba un número entero de longitudes de onda, esperaba ver interferencia constructiva; cuando este retraso representaba un número medio entero de longitudes de onda, esperaba ver interferencia destructiva. En ausencia de arrastre, su expectativa era que el espectro observado fuera continuo con el aparato orientado transversalmente al viento de éter, y que estuviera en bandas con el aparato orientado en paralelo al viento de éter. Sus resultados experimentales reales fueron completamente negativos.

Éleuthère Mascart (1872) demostró un resultado para la luz polarizada que viaja a través de un medio birrefringente que da diferentes velocidades de acuerdo con la fórmula empírica de Fresnel. Sin embargo, el resultado en términos del modelo físico de Fresnel requiere un arrastre de éter diferente en diferentes direcciones en el medio.

Albert A. Michelson y Edward W. Morley (1886) repitieron el experimento de Fizeau con mayor precisión, abordando varias preocupaciones con el experimento original de Fizeau: (1) La deformación de los componentes ópticos en el aparato de Fizeau podría causar desplazamiento de franjas por artefactos; (2) las observaciones se hicieron apresuradamente, ya que el flujo de agua presurizado duró poco tiempo; (3) el perfil de flujo laminar del agua que fluía a través de los tubos de diámetro pequeño de Fizeau significaba que solo estaban disponibles sus porciones centrales, lo que resultaba en franjas tenues; (4) había incertidumbres en la determinación de Fizeau de la velocidad de flujo a través del diámetro de los tubos. Michelson rediseñó el aparato de Fizeau con tubos de mayor diámetro y un gran depósito que proporcionaba tres minutos de flujo de agua constante. Su diseño de interferómetro de trayectoria común proporcionó una compensación automática de la longitud de la trayectoria, de modo que las franjas de luz blanca eran visibles de inmediato tan pronto como se alineaban los elementos ópticos. Topológicamente, el recorrido de la luz era el de un interferómetro de Sagnac con un número par de reflexiones en cada recorrido de luz. Esto ofrecía franjas extremadamente estables que eran, en primer orden, completamente insensibles a cualquier movimiento de sus componentes ópticos. La estabilidad era tal que le era posible insertar una placa de vidrio a h o incluso sostener una cerilla encendida en el recorrido de la luz sin desplazar el centro del sistema de franjas. Con este aparato, Michelson y Morley pudieron confirmar completamente los resultados de Fizeau no sólo en el agua, sino también en el aire.

En 1895, Hendrik Lorentz predijo la existencia de un término extra debido a la dispersión:

${\displaystyle w_{+}={\frac {c}{n}+v\left(1-{\frac} {1}{n^{2}}-{\frac} {\fnMicrode {\fn} {\fn}\cdot \! {\fn} {\m} {\m\mhm {d} \lambda}}\right)}\$

Dado que el medio fluye hacia el observador o alejándose de él, la luz que viaja a través del medio sufre un desplazamiento Doppler, y el índice de refracción utilizado en la fórmula tiene que ser el apropiado para la longitud de onda desplazada por el efecto Doppler. Zeeman verificó la existencia del término de dispersión de Lorentz en 1915. Utilizando una versión ampliada del aparato de Michelson conectado directamente al conducto principal de agua de Ámsterdam, Zeeman pudo realizar mediciones extendidas utilizando luz monocromática que abarcaba desde el violeta (4358 Å) hasta el rojo (6870 Å) para confirmar el coeficiente modificado de Lorentz.

En 1910, Franz Harress utilizó un dispositivo giratorio y confirmó en general el coeficiente de arrastre de Fresnel. Sin embargo, también encontró un "sesgo sistemático" en los datos, que más tarde resultó ser el efecto Sagnac.

Desde entonces, se han llevado a cabo numerosos experimentos para medir dichos coeficientes de arrastre en una variedad de materiales con diferentes índices de refracción, a menudo en combinación con el efecto Sagnac. Por ejemplo, en experimentos que utilizan láseres de anillo junto con discos giratorios, o en experimentos de interferometría de neutrones. También se observó un efecto de arrastre transversal, es decir, cuando el medio se mueve en ángulos rectos con respecto a la dirección de la luz incidente.

En 1892, Hendrik Lorentz propuso una modificación del modelo de Fresnel, en el que el éter es completamente estacionario. Logró derivar el coeficiente de arrastre de Fresnel como resultado de una interacción entre el agua en movimiento y un éter no arrastrado. También descubrió que la transición de un sistema de referencia a otro podía simplificarse utilizando una variable temporal auxiliar a la que llamó tiempo local:

${\displaystyle t^{\prime }=t-{\frac {vx}{c^{2}}\$

En 1895, Lorentz explicó de forma más general el coeficiente de Fresnel basándose en el concepto de tiempo local. Sin embargo, la teoría de Lorentz tenía el mismo problema fundamental que la de Fresnel: un éter estacionario contradecía el experimento de Michelson-Morley. Así, en 1892, Lorentz propuso que los cuerpos en movimiento se contraen en la dirección del movimiento (hipótesis de contracción de FitzGerald-Lorentz, ya que George FitzGerald había llegado a esta conclusión en 1889). Las ecuaciones que utilizó para describir estos efectos fueron desarrolladas por él hasta 1904. Ahora se denominan transformaciones de Lorentz en su honor y son idénticas en su forma a las ecuaciones que Einstein derivaría posteriormente a partir de los primeros principios. Sin embargo, a diferencia de las ecuaciones de Einstein, las transformaciones de Lorentz eran estrictamente ad hoc, y su única justificación era que parecían funcionar.

Einstein demostró cómo las ecuaciones de Lorentz podían derivarse como el resultado lógico de un conjunto de dos postulados iniciales simples. Además, Einstein reconoció que el concepto de éter estacionario no tiene cabida en la relatividad especial y que la transformación de Lorentz concierne a la naturaleza del espacio y el tiempo. Junto con el problema del imán y el conductor en movimiento, los experimentos de deriva negativa del éter y la aberración de la luz, el experimento de Fizeau fue uno de los resultados experimentales clave que moldearon el pensamiento de Einstein sobre la relatividad. Robert S. Shankland informó sobre algunas conversaciones con Einstein, en las que Einstein enfatizó la importancia del experimento de Fizeau:

Continuó diciendo que los resultados experimentales que más le habían influido fueron las observaciones de la aberración estelar y las mediciones de Fizeau sobre la velocidad de la luz en el agua en movimiento. "Fueron suficientes", dijo.

Max von Laue (1907) demostró que el coeficiente de arrastre de Fresnel se puede explicar como una consecuencia natural de la fórmula relativista para la adición de velocidades. La velocidad de la luz en agua inmóvil es c/n. De la ley de composición de velocidad sigue que la velocidad de luz observada en el laboratorio, donde el agua fluye con velocidad v (en la misma dirección que la luz) $${\displaystyle V_{\mathrm}={\frac {\frac} {\fn}}+v}{1+{\frac {\fnh} {\fn} {\fn} {\fn} {\fn} {\fn} {\fn} {\fn} {\fn} {\fn} {\fn}\fn} {\f}\fn} {\fn} {\f}\fn}\f}\f}\fn}}}}}\fn}}}}}}}}}}}}}}}}}}}}}\\\\\\\\\p}\f}\\p}\p}\p}\fn}}\\\\\\f}\f}\p}\p}\p}\p}\p}\p}\p}\c}\p}\p}\p\p\p\p}\p}\p}\p}\p}\p}\p}\p}\p}\p}\p}\p}\p}\p}\p} {} {\fn} {\fn}} {\fn}}}} {\fn}}} {\fn}}} {\f}}}}}} {\fn}}} {\fn}}}}}} {\fn}}}}} {\f}}}} {\f}}}}} {\f}}}}}}}}}}}}}}}}}}}}}} {\ {\fnMicroc {c}{n}+v}{1+{\frac} {v} {cn}}}\fnMicros}$$Así la diferencia de velocidad es (suponiendo v es pequeño comparando con c, bajando los términos del orden superior) $${\displaystyle V_{\mathrm}-{\frac} {C} {\fn}={\frac} {\fnK} {\fn} {\fn} {\fn} {\fn}} {\fn}\fn}\fn} {\fn} {\fn\fn}\fn}\fn} {\fn}\fn}\fn\fn\fn}\fn}\f}\fn\fn}\\fn\fn}\\fn\fnh\fn\fn}\fn}\fn\fn}\fn}\fn\fn\fn}\fn\fn\fn}\fn\fn\fn}\\\fn\\fnh\fn}\fnh\fn}\fn}\\\fn\fn\fn\fn}\fn\fn}\fn}\fnh\fn}\\fn}\\\\\\fn}\\\\fn {c}{n}+v}{1+{\frac} {C}} {\fn} {\fnK}} {\fn}}} {\fn}}} {\fn} {\fn}} {\fn}} {\fn}} {\fnK}}}}}}} {\fn}} {\fn\f}}} {\fn\fnMicroc}} {\f}}}}} {\f}}}}}}}}}}}} {\f}}}}}}}}} {\f}}}}}}}} {\f}}}}}} {\f}}}}}}} {\f}} {\f}}}}}}}}}}}} {\f} {\f}} {\f} {\f}} {\f}}}} {\f}}}}}\f}\f}}}}}}}}}}}}}}}}\f}}}}}}}}}}}}}}}}}}}}}}} {c} {n}={\frac} {\fnMicroc {c} {n}+v-{\frac} {c}{n}(1+{\frac} {v}{cn}) }{1+{\frac {C}}}$$ $${\displaystyle ={\frac {v\left(1-{\frac {1}{n^{2}}\right)}{1+{\frac} . v\left(1-{\frac {1}\right)\$$Esto es preciso cuando v/c 1, y está de acuerdo con la fórmula basada en las mediciones de Fizeau, que satisfizo la condición v/c 1.

Alternativamente, el resultado de Fizeau se puede obtener aplicando las ecuaciones de Maxwell a un medio en movimiento.

• Pruebas de relatividad especial
• Hipótesis de arrastre de éter
• Historia de la relatividad especial

Fuentes secundarias

Fuentes primarias