Experimento de doble rendija

Los fotones o partículas de materia (como un electrón) producen un patrón de onda cuando se usan dos rendijas

Luz de un láser verde pasando por dos aberturas 0.4mm de ancho y 0.1mm de distancia

En la física moderna, el experimento de la doble rendija es una demostración de que la luz y la materia pueden mostrar características tanto de ondas como de partículas clásicamente definidas; además, muestra la naturaleza fundamentalmente probabilística de los fenómenos mecánicos cuánticos. Este tipo de experimento fue realizado por primera vez por Thomas Young en 1801, como demostración del comportamiento ondulatorio de la luz visible. En ese momento se pensaba que la luz consistía en o ondas o partículas. Con el comienzo de la física moderna, unos cien años después, se descubrió que la luz podía mostrar un comportamiento característico de ambas ondas y partículas. En 1927, Davisson y Germer demostraron que los electrones muestran el mismo comportamiento, que luego se extendió a los átomos y moléculas. El experimento de Thomas Young con la luz fue parte de la física clásica mucho antes del desarrollo de la mecánica cuántica y el concepto de dualidad onda-partícula. Creía que demostraba que la teoría ondulatoria de la luz era correcta, y su experimento a veces se denomina experimento de Young o rendijas de Young.

El experimento pertenece a una clase general de "doble camino" experimentos, en los que una onda se divide en dos ondas separadas (la onda generalmente está formada por muchos fotones y es mejor denominarla frente de onda, que no debe confundirse con las propiedades de onda del fotón individual) que luego se combinan en una sola onda. Los cambios en las longitudes de trayectoria de ambas ondas dan como resultado un cambio de fase, creando un patrón de interferencia. Otra versión es el interferómetro Mach-Zehnder, que divide el haz con un divisor de haz.

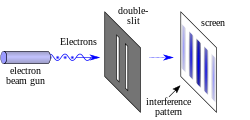
En la versión básica de este experimento, una fuente de luz coherente, como un rayo láser, ilumina una placa perforada por dos rendijas paralelas y la luz que pasa a través de las rendijas se observa en una pantalla detrás de la placa. La naturaleza ondulatoria de la luz hace que las ondas de luz que pasan a través de las dos rendijas interfieran, produciendo bandas brillantes y oscuras en la pantalla, un resultado que no se esperaría si la luz consistiera en partículas clásicas. Sin embargo, siempre se encuentra que la luz es absorbida en la pantalla en puntos discretos, como partículas individuales (no ondas); el patrón de interferencia aparece a través de la densidad variable de estos impactos de partículas en la pantalla. Además, las versiones del experimento que incluyen detectores en las rendijas encuentran que cada fotón detectado pasa a través de una rendija (como lo haría una partícula clásica), y no a través de ambas rendijas (como lo haría una onda). Sin embargo, tales experimentos demuestran que las partículas no forman el patrón de interferencia si uno detecta por qué rendija pasan. Estos resultados demuestran el principio de la dualidad onda-partícula.

Otras entidades a escala atómica, como los electrones, exhiben el mismo comportamiento cuando se disparan hacia una doble rendija. Además, se observa que la detección de impactos discretos individuales es inherentemente probabilística, lo cual es inexplicable utilizando la mecánica clásica.

El experimento se puede realizar con entidades mucho más grandes que los electrones y los fotones, aunque se vuelve más difícil a medida que aumenta el tamaño. Las entidades más grandes para las que se realizó el experimento de la doble rendija fueron moléculas que comprendían cada una 2000 átomos (cuya masa total era de 25 000 unidades de masa atómica).

El experimento de la doble rendija (y sus variaciones) se ha convertido en un clásico por su claridad al expresar los enigmas centrales de la mecánica cuántica. Debido a que demuestra la limitación fundamental de la capacidad del observador para predecir los resultados experimentales, Richard Feynman lo llamó "un fenómeno que es imposible [...] de explicar de forma clásica, y que tiene en sí mismo el corazón de la mecánica cuántica".. En realidad, contiene el único misterio [de la mecánica cuántica]."

Resumen

El mismo montaje de doble corte (0,7 mm entre las aberturas); en la imagen superior, una abertura está cerrada. En la imagen de una sola abertura, se forma un patrón de difracción (los puntos débiles de cada lado de la banda principal) debido a la anchura no cero de la abertura. Este patrón de difracción también se ve en la imagen doble, pero con muchos flecos de interferencia más pequeños.

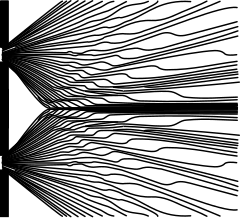
Si la luz consistiera estrictamente en partículas ordinarias o clásicas, y estas partículas se dispararan en línea recta a través de una rendija y se dejaran golpear una pantalla en el otro lado, esperaríamos ver un patrón correspondiente al tamaño y la forma de la hendidura Sin embargo, cuando este "experimento de una sola rendija" se realiza realmente, el patrón en la pantalla es un patrón de difracción en el que la luz se dispersa. Cuanto menor sea la rendija, mayor será el ángulo de propagación. La parte superior de la imagen muestra la parte central del patrón que se forma cuando un láser rojo ilumina una hendidura y, si se mira con cuidado, dos bandas laterales tenues. Se pueden ver más bandas con un aparato más refinado. La difracción explica el patrón como el resultado de la interferencia de las ondas de luz de la rendija.

Si uno ilumina dos rendijas paralelas, la luz de las dos rendijas nuevamente interfiere. Aquí la interferencia es un patrón más pronunciado con una serie de bandas claras y oscuras alternas. El ancho de las bandas es una propiedad de la frecuencia de la luz que ilumina. (Vea la fotografía inferior a la derecha). Cuando Thomas Young (1773–1829) demostró por primera vez este fenómeno, indicó que la luz consta de ondas, ya que la distribución del brillo puede explicarse por la interferencia alternativamente aditiva y sustractiva de los frentes de onda. El experimento de Young, realizado a principios del siglo XIX, desempeñó un papel crucial en la comprensión de la teoría ondulatoria de la luz, superando la teoría corpuscular de la luz propuesta por Isaac Newton, que había sido el modelo aceptado de propagación de la luz en el siglo XVII. y los siglos XVIII. Sin embargo, el posterior descubrimiento del efecto fotoeléctrico demostró que, en diferentes circunstancias, la luz puede comportarse como si estuviera compuesta de partículas discretas. Estos descubrimientos aparentemente contradictorios hicieron necesario ir más allá de la física clásica y tener en cuenta la naturaleza cuántica de la luz.

A Feynman le gustaba decir que toda la mecánica cuántica se puede deducir al pensar detenidamente en las implicaciones de este único experimento. También propuso (como experimento mental) que si se colocaran detectores antes de cada rendija, el patrón de interferencia desaparecería.

La relación de dualidad de Englert-Greenberger proporciona un tratamiento detallado de las matemáticas de la interferencia de doble rendija en el contexto de la mecánica cuántica.

G. I. Taylor realizó por primera vez un experimento de doble rendija de baja intensidad en 1909, al reducir el nivel de luz incidente hasta que los eventos de emisión/absorción de fotones no se superpusieran en su mayoría. Un experimento de doble rendija no se realizó con nada más que luz hasta 1961, cuando Claus Jönsson de la Universidad de Tübingen lo realizó con haces de electrones. En 1974, los físicos italianos Pier Giorgio Merli, Gian Franco Missiroli y Giulio Pozzi repitieron el experimento usando electrones individuales y biprisma (en lugar de rendijas), demostrando que cada electrón interfiere consigo mismo como predice la teoría cuántica. En 2002, la versión de un solo electrón del experimento fue votada como "el experimento más hermoso" por los lectores de Physics World.

En 2012, Stefano Frabboni y sus colaboradores finalmente realizaron el experimento de la doble rendija con electrones y rendijas reales, siguiendo el esquema original propuesto por Feynman. Enviaron electrones individuales a rendijas nanofabricadas (de unos 100 nm de ancho) y, al recopilar los electrones transmitidos con un detector de un solo electrón, pudieron mostrar la acumulación de un patrón de interferencia de doble rendija.

En 2018, un grupo dirigido por Marco Giammarchi demostró por primera vez la interferencia de una sola partícula para la antimateria en el Laboratorio de positrones (L-NESS, Politecnico di Milano) de Rafael Ferragut en Como (Italia).

Variaciones del experimento

Interferencia de partículas individuales

Configuración del patrón de interferencia de las detecciones individuales de partículas

Una versión importante de este experimento implica partículas individuales. El envío de partículas a través de un aparato de doble rendija, una a la vez, da como resultado que aparezcan partículas individuales en la pantalla, como se esperaba. Sorprendentemente, sin embargo, surge un patrón de interferencia cuando se permite que estas partículas se acumulen una por una (ver la imagen adyacente). Esto demuestra la dualidad onda-partícula, que establece que toda la materia exhibe propiedades tanto de onda como de partícula: la partícula se mide como un solo pulso en una sola posición, mientras que la onda describe la probabilidad de absorber la partícula en un lugar específico de la pantalla.. Se ha demostrado que este fenómeno ocurre con fotones, electrones, átomos e incluso algunas moléculas. El éxito se logró con buckminsterfullereno (C
₆₀) en 2001, con 2 moléculas de 430 átomos (C
₆₀(C
₁₂F
₂₅)
₁₀ y C
₁₆₈H
₉₄F
₁₅₂O
₈N
₄S
₄) en 2011, y con moléculas de hasta 2000 átomos en 2019.

La probabilidad de detección es el cuadrado de la amplitud de la onda y se puede calcular con ondas clásicas (ver más abajo). Desde el origen de la mecánica cuántica, algunos teóricos han buscado formas de incorporar determinantes adicionales o "variables ocultas" que, si se llegaran a conocer, darían cuenta de la ubicación de cada impacto individual con el objetivo.

Interferómetro Mach-Zehnder

Los fotones de un interferómetro Mach–Zehnder exhiben interferencia de onda y detección de partículas en detectores de un solo fotón.

El interferómetro de Mach-Zehnder puede verse como una versión simplificada del experimento de la doble rendija. En lugar de propagarse a través del espacio libre después de las dos rendijas y golpear cualquier posición en una pantalla extendida, en el interferómetro los fotones solo pueden propagarse a través de dos caminos y golpear dos fotodetectores discretos. Esto hace posible describirlo mediante álgebra lineal simple en dimensión 2, en lugar de ecuaciones diferenciales.

Un fotón emitido por el láser golpea el primer divisor de haz y luego se encuentra en una superposición entre los dos caminos posibles. En el segundo divisor de haz estos caminos interfieren, haciendo que el fotón golpee el fotodetector de la derecha con probabilidad uno, y el fotodetector de abajo con probabilidad cero. Es interesante considerar qué sucedería si el fotón estuviera definitivamente en cualquiera de los caminos entre los divisores de haz. Esto se puede lograr bloqueando uno de los caminos o, de manera equivalente, detectando la presencia de un fotón allí. En ambos casos, ya no habrá interferencia entre las rutas y ambos fotodetectores se verán afectados con una probabilidad de 1/2. De esto podemos concluir que el fotón no toma un camino u otro después del primer divisor de haz, sino que se encuentra en una genuina superposición cuántica de los dos caminos.

"Hacia dónde" experimentos y el principio de complementariedad

Un conocido experimento mental predice que si se colocan detectores de partículas en las rendijas, mostrando a través de qué rendija pasa un fotón, el patrón de interferencia desaparecerá. Este experimento de qué dirección ilustra el principio de complementariedad de que los fotones pueden comportarse como partículas u ondas, pero no pueden observarse como ambas al mismo tiempo. A pesar de la importancia de este experimento mental en la historia de la mecánica cuántica (por ejemplo, véase la discusión sobre la versión de este experimento de Einstein), no se propusieron realizaciones técnicamente factibles de este experimento hasta la década de 1970. (Las implementaciones ingenuas del experimento mental de los libros de texto no son posibles porque los fotones no se pueden detectar sin absorber el fotón). Actualmente, se han realizado múltiples experimentos que ilustran varios aspectos de la complementariedad.

Un experimento realizado en 1987 produjo resultados que demostraron que se podía obtener información sobre qué camino había tomado una partícula sin destruir la interferencia por completo. Esto mostró el efecto de las mediciones que perturbaron las partículas en tránsito en menor grado y, por lo tanto, influyeron en el patrón de interferencia solo en un grado comparable. En otras palabras, si uno no insiste en que el método utilizado para determinar por qué rendija pasa cada fotón sea completamente confiable, aún puede detectar un patrón de interferencia (degradado).

Elección retrasada y variaciones del borrador cuántico

Un diagrama del experimento de elección retardada de Wheeler, mostrando el principio de determinar el camino del foton después de pasar por la abertura

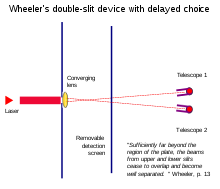
Los experimentos de elección retrasada de Wheeler demuestran que extraer "qué ruta" la información después de que una partícula pasa a través de las rendijas puede parecer que altera retroactivamente su comportamiento anterior en las rendijas.

Los experimentos con el borrador cuántico demuestran que el comportamiento de las ondas se puede restaurar borrando o haciendo que no esté disponible de forma permanente la ruta "qué ruta" información.

En un artículo de Scientific American se proporcionó una ilustración sencilla del fenómeno del borrador cuántico que se puede hacer en casa. Si se colocan polarizadores antes de cada rendija con sus ejes ortogonales entre sí, se eliminará el patrón de interferencia. Se puede considerar que los polarizadores introducen información de qué camino para cada haz. Introduciendo un tercer polarizador delante del detector con un eje de 45° respecto a los demás polarizadores "borra" esta información, permitiendo que el patrón de interferencia reaparezca. Esto también se puede explicar si se considera que la luz es una onda clásica y también si se utilizan polarizadores circulares y fotones individuales. Las implementaciones de los polarizadores que utilizan pares de fotones entrelazados no tienen una explicación clásica.

Medición débil

En un experimento muy publicitado en 2012, los investigadores afirmaron haber identificado el camino que había tomado cada partícula sin ningún efecto adverso en el patrón de interferencia generado por las partículas. Para hacer esto, utilizaron una configuración tal que las partículas que llegaban a la pantalla no procedían de una fuente puntual, sino de una fuente con dos intensidades máximas. Sin embargo, comentaristas como Svensson han señalado que, de hecho, no existe conflicto entre las mediciones débiles realizadas en esta variante del experimento de la doble rendija y el principio de incertidumbre de Heisenberg. La medición débil seguida de una selección posterior no permitió mediciones simultáneas de posición y momento para cada partícula individual, sino que permitió la medición de la trayectoria promedio de las partículas que llegaron a diferentes posiciones. En otras palabras, los experimentadores estaban creando un mapa estadístico del paisaje de trayectoria completo.

Otras variaciones

Un montaje de doble corte de laboratorio; distancia entre los postes superiores de aproximadamente 2,5 cm (una pulgada).

Pautas de distribución de intensidad de campo cercano para las aberturas plasmónicas con anchos iguales (A) y anchos no iguales (B).

En 1967, Pfleegor y Mandel demostraron la interferencia de dos fuentes usando dos láseres separados como fuentes de luz.

Se demostró experimentalmente en 1972 que en un sistema de doble rendija donde solo una rendija estaba abierta en cualquier momento, se observó interferencia siempre que la diferencia de camino fuera tal que el fotón detectado podría haber venido de cualquiera de las dos rendijas. Las condiciones experimentales eran tales que la densidad de fotones en el sistema era mucho menor que la unidad.

En 1999, se realizó con éxito un experimento de interferencia cuántica (utilizando una rejilla de difracción, en lugar de dos rendijas) con moléculas de bola de Bucky (cada una de las cuales consta de 60 átomos de carbono). Una bola de Bucky es lo suficientemente grande (diámetro de alrededor de 0,7 nm, casi medio millón de veces más grande que un protón) para ser vista bajo un microscopio electrónico.

En 2005, E. R. Eliel presentó un estudio experimental y teórico de la transmisión óptica de una delgada pantalla de metal perforada por dos rendijas de sublongitud de onda, separadas por muchas longitudes de onda ópticas. Se muestra que la intensidad total del patrón de doble rendija de campo lejano se reduce o aumenta en función de la longitud de onda del haz de luz incidente.

En 2012, investigadores de la Universidad de Nebraska–Lincoln realizaron el experimento de doble rendija con electrones descrito por Richard Feynman, utilizando nuevos instrumentos que permitieron controlar la transmisión de las dos rendijas y monitorear eventos de detección de un solo electrón.. Los electrones fueron disparados por un cañón de electrones y pasaron a través de una o dos rendijas de 62 nm de ancho × 4 μm de alto.

En 2013, se realizó con éxito un experimento de interferencia cuántica (usando rejillas de difracción en lugar de dos rendijas) con moléculas de 810 átomos cada una (cuya masa total superaba las 10 000 unidades de masa atómica). El récord se elevó a 2000 átomos (25.000 amu) en 2019.

Análogos hidrodinámicos de onda piloto

Se han desarrollado análogos hidrodinámicos que pueden recrear varios aspectos de los sistemas mecánicos cuánticos, incluida la interferencia de una sola partícula a través de una doble rendija. Una gota de aceite de silicona, que rebota a lo largo de la superficie de un líquido, se autopropulsa a través de interacciones resonantes con su propio campo de ondas. La gota salpica suavemente el líquido con cada rebote. Al mismo tiempo, las ondas de rebotes anteriores afectan su curso. La interacción de la gota con sus propias ondas, que forman lo que se conoce como onda piloto, hace que muestre comportamientos que antes se pensaba que eran peculiares de las partículas elementales, incluidos los comportamientos que habitualmente se toman como evidencia de que las partículas elementales se esparcen por el espacio como ondas, sin ninguna ubicación específica, hasta que se miden.

Los comportamientos imitados a través de este sistema hidrodinámico de onda piloto incluyen difracción cuántica de partículas individuales, tunelización, órbitas cuantificadas, división de nivel orbital, espín y estadísticas multimodales. También es posible inferir relaciones de incertidumbre y principios de exclusión. Hay videos disponibles que ilustran varias características de este sistema. (Consulte los enlaces externos).

Sin embargo, los sistemas más complicados que involucran dos o más partículas en superposición no son susceptibles de una explicación tan simple e intuitiva clásica. En consecuencia, no se ha desarrollado ningún análogo hidrodinámico del entrelazamiento. Sin embargo, los análogos ópticos son posibles.

Formulación clásica de ondas ópticas

Patrón de difracción de dos litros por onda de avión

Foto de la interferencia doble de la luz solar.

Dos aberturas están iluminadas por una ola de avión.

Gran parte del comportamiento de la luz se puede modelar mediante la teoría ondulatoria clásica. El principio de Huygens-Fresnel es uno de esos modelos; establece que cada punto en un frente de onda genera una ondícula secundaria, y que la perturbación en cualquier punto posterior se puede encontrar sumando las contribuciones de las ondas individuales en ese punto. Esta suma debe tener en cuenta tanto la fase como la amplitud de las ondículas individuales. Solo se puede medir la intensidad de un campo de luz, que es proporcional al cuadrado de la amplitud.

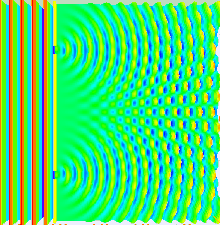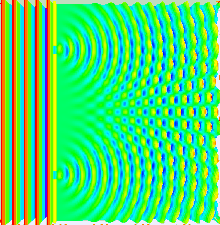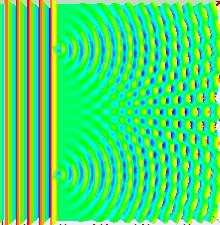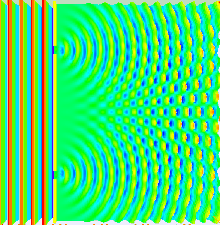
En el experimento de la doble rendija, las dos rendijas se iluminan con la luz casi monocromática de un solo láser. Si el ancho de las rendijas es lo suficientemente pequeño (mucho menor que la longitud de onda de la luz láser), las rendijas difractan la luz en ondas cilíndricas. Estos dos frentes de onda cilíndricos están superpuestos, y la amplitud, y por lo tanto la intensidad, en cualquier punto de los frentes de onda combinados depende tanto de la magnitud como de la fase de los dos frentes de onda. La diferencia de fase entre las dos ondas está determinada por la diferencia en la distancia recorrida por las dos ondas.

Si la distancia de visualización es grande en comparación con la separación de las rendijas (el campo lejano), la diferencia de fase se puede encontrar utilizando la geometría que se muestra en la figura de abajo a la derecha. La diferencia de trayectoria entre dos ondas que viajan en un ángulo θ viene dada por:

dpecado⁡ ⁡ Silencio Silencio .. dSilencio Silencio {displaystyle dsin theta approx dtheta }

Donde d es la distancia entre las dos rendijas. Cuando las dos ondas están en fase, es decir, la diferencia de trayectoria es igual a un número entero de longitudes de onda, la amplitud sumada y, por lo tanto, la intensidad sumada es máxima, y cuando están en oposición de fase, es decir, la diferencia de trayectoria es igual a la mitad. una longitud de onda, una longitud de onda y media, etc., entonces las dos ondas se cancelan y la intensidad sumada es cero. Este efecto se conoce como interferencia. Los máximos de la franja de interferencia se producen en ángulos

dSilencio Silencio n=nλ λ ,n=0,1,2,...... {displaystyle ~dtheta _{n}=nlambda~n=0,1,2,ldots }

donde λ es la longitud de onda de la luz. El espaciado angular de las franjas, θ_f, viene dado por

Silencio Silencio f.. λ λ /d{displaystyle theta _{f}approx lambda /d}

El espaciado de las franjas a una distancia z de las rendijas está dado por

w=zSilencio Silencio f=zλ λ /d{displaystyle ~w=ztheta ¿Qué? /d}

Por ejemplo, si dos rendijas están separadas por 0,5 mm (d) y se iluminan con un láser de longitud de onda de 0,6 μm (λ), luego a una distancia de 1 m (z), el espaciado de las franjas será de 1,2 milímetro

Si el ancho de las rendijas b es apreciable en comparación con la longitud de onda, se necesita la ecuación de difracción de Fraunhofer para determinar la intensidad de la luz difractada como sigue:

I()Silencio Silencio )∝ ∝ #2⁡ ⁡ [π π dpecado⁡ ⁡ Silencio Silencio λ λ ]sinc2[π π bpecado⁡ ⁡ Silencio Silencio λ λ ]{displaystyle {begin{aligned}I(theta) ventajapropto cos ^{2}left[{frac] {pi dsintheta }{lambda }right]~mathrm {sinc}left[{frac {pi bsin theta] } {lambda }derecha]end{aligned}}

donde la función sinc se define como sinc(x) = sin(x)/x para x ≠ 0, y sinc(0) = 1.

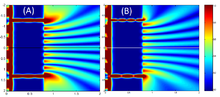
Esto se ilustra en la figura anterior, donde el primer patrón es el patrón de difracción de una sola rendija, dado por la función sinc en esta ecuación, y la segunda figura muestra la intensidad combinada de la luz difractada por las dos rendijas, donde la función cos representa la estructura fina, y la estructura más gruesa representa la difracción por las rendijas individuales como se describe en la sinc función.

Se pueden realizar cálculos similares para el campo cercano aplicando la ecuación de difracción de Fresnel, lo que implica que a medida que el plano de observación se acerca al plano en el que se encuentran las rendijas, los patrones de difracción asociados con cada rendija disminuyen de tamaño, de modo que el área en la que se produce la interferencia se reduce y puede desaparecer por completo cuando no hay superposición en los dos patrones difractados.

Interpretaciones del experimento

Al igual que el experimento mental del gato de Schrödinger, el experimento de la doble rendija se usa a menudo para resaltar las diferencias y similitudes entre las diversas interpretaciones de la mecánica cuántica.

Interpretación de Copenhague

La interpretación de Copenhague, presentada por algunos de los pioneros en el campo de la mecánica cuántica, afirma que no es deseable postular algo que vaya más allá de las fórmulas matemáticas y los tipos de aparatos físicos y reacciones que nos permiten obtener algún conocimiento. de lo que sucede a escala atómica. Una de las construcciones matemáticas que permite a los experimentadores predecir con mucha precisión ciertos resultados experimentales a veces se denomina onda de probabilidad. En su forma matemática es análoga a la descripción de una onda física, pero sus "crestas" y "canales" indican los niveles de probabilidad de que ocurran ciertos fenómenos (por ejemplo, una chispa de luz en un punto determinado de la pantalla de un detector) que se pueden observar en el mundo macro de la experiencia humana ordinaria.

La probabilidad "onda" se puede decir que "atraviesa el espacio" porque los valores de probabilidad que se pueden calcular a partir de su representación matemática dependen del tiempo. No se puede hablar de la ubicación de cualquier partícula, como un fotón, entre el momento en que se emite y el momento en que se detecta simplemente porque para decir que algo está ubicado en algún lugar en un momento determinado, hay que detectarlo. El requisito para la eventual aparición de un patrón de interferencia es que se emitan partículas y que haya una pantalla con al menos dos caminos distintos para que la partícula tome desde el emisor hasta la pantalla de detección. Los experimentos no observan nada en absoluto entre el tiempo de emisión de la partícula y su llegada a la pantalla de detección. Si a continuación se realiza un trazado de rayos como si una onda de luz (tal como se entiende en la física clásica) fuera lo suficientemente ancha como para tomar ambos caminos, entonces ese trazado de rayos predecirá con precisión la aparición de máximos y mínimos en la pantalla del detector cuando muchas partículas pasan a través de la aparato y gradualmente "pintar" el patrón de interferencia esperado.

Formulación integral de ruta

Uno de un número infinito de caminos igualmente probables utilizados en la ruta de Feynman integral (ver también: proceso de Wiener)

La interpretación de Copenhague es similar a la formulación de la integral de trayectoria de la mecánica cuántica proporcionada por Feynman. La formulación de la integral de trayectoria reemplaza la noción clásica de una trayectoria única y única para un sistema, con una suma de todas las trayectorias posibles. Las trayectorias se suman mediante integración funcional.

Cada ruta se considera igualmente probable y, por lo tanto, contribuye con la misma cantidad. Sin embargo, la fase de esta contribución en cualquier punto dado a lo largo del camino está determinada por la acción a lo largo del camino:

Asendero()x,Sí.,z,t)=eiS()x,Sí.,z,t){displaystyle A_{text{path}(x,y,z,t)=e^{iS(x,y,z,t)}

Todas estas contribuciones se suman y la magnitud del resultado final se eleva al cuadrado para obtener la distribución de probabilidad de la posición de una partícula:

p()x,Sí.,z,t)∝ ∝ Silencio∫ ∫ todos los caminoseiS()x,Sí.,z,t)Silencio2{displaystyle p(x,y,z,t)propto leftvert int _{text{all paths}}e^{iS(x,y,z,t)}rightvert ^{2}}

Como siempre ocurre cuando se calcula la probabilidad, los resultados deben normalizarse imponiendo:

∫ ∫ todo el espaciop()x,Sí.,z,t)dV=1{displaystyle iiint _{text{all space}p(x,y,z,t),dV=1}

Para resumir, la distribución de probabilidad del resultado es el cuadrado normalizado de la norma de la superposición, sobre todos los caminos desde el punto de origen hasta el punto final, de ondas que se propagan proporcionalmente a la acción a lo largo de cada camino. Las diferencias en la acción acumulativa a lo largo de los diferentes caminos (y, por lo tanto, las fases relativas de las contribuciones) producen el patrón de interferencia observado por el experimento de la doble rendija. Feynman enfatizó que su formulación es simplemente una descripción matemática, no un intento de describir un proceso real que podamos medir.

Interpretación relacional

Ejemplo del principio de incertidumbre relacionado con la interpretación relacional. Cuanto más se conoce sobre la posición de una partícula, menos se conoce sobre la velocidad y viceversa

Según la interpretación relacional de la mecánica cuántica, propuesta por primera vez por Carlo Rovelli, las observaciones como las del experimento de la doble rendija resultan específicamente de la interacción entre el observador (dispositivo de medición) y el objeto observado (con el que se interactúa físicamente), no cualquier propiedad absoluta poseída por el objeto. En el caso de un electrón, si inicialmente se "observa" en una rendija en particular, la interacción observador-partícula (fotón-electrón) incluye información sobre la posición del electrón. Esto restringe parcialmente la ubicación final de la partícula en la pantalla. Si se "observa" (medido con un fotón) no en una rendija en particular sino en la pantalla, entonces no hay 'qué camino' información como parte de la interacción, por lo que el electrón es 'observado'. la posición en la pantalla está determinada estrictamente por su función de probabilidad. Esto hace que el patrón resultante en la pantalla sea el mismo que si cada electrón individual hubiera pasado por ambas rendijas.

Interpretación de muchos mundos

El físico David Deutsch argumenta en su libro The Fabric of Reality que el experimento de la doble rendija es evidencia de la interpretación de muchos mundos. Sin embargo, dado que cada interpretación de la mecánica cuántica es empíricamente indistinguible, algunos científicos se muestran escépticos ante esta afirmación.

Teoría de De Broglie-Bohm

Una alternativa a la comprensión estándar de la mecánica cuántica, la teoría de De Broglie-Bohm establece que las partículas también tienen ubicaciones precisas en todo momento y que sus velocidades están definidas por la función de onda. Entonces, mientras que una sola partícula viajará a través de una rendija en particular en el experimento de doble rendija, la llamada 'onda piloto' que influye viajará a través de ambos. Las dos trayectorias de la rendija de Broglie-Bohm fueron calculadas por primera vez por Chris Dewdney mientras trabajaba con Chris Philippidis y Basil Hiley en Birkbeck College (Londres). La teoría de de Broglie-Bohm produce los mismos resultados estadísticos que la mecánica cuántica estándar, pero prescinde de muchas de sus dificultades conceptuales.

Trayectorias bohmianas

Trayectorias de partículas bajo la teoría de De Broglie-Bohm en el experimento de doble corte.

100 trayectorias guiadas por la función de onda. En la teoría de De Broglie-Bohm, una partícula está representada, en cualquier momento, por una función de onda y una posición (centro de masa). Esta es una especie de realidad aumentada en comparación con la interpretación estándar.

simulación numérica del experimento de doble corte con electrones. Figura a la izquierda: evolución (de izquierda a derecha) de la intensidad del haz de electrones en la salida de las hendiduras (izquierda) hasta la pantalla de detección situada 10 cm después de las hendiduras (derecha). Cuanto mayor sea la intensidad, más color es azul claro - Figura en el centro: impactos de los electrones observados en la pantalla - Figura a la derecha: intensidad de los electrones en el campo lejano aproximación (en la pantalla). Datos numéricos del experimento de Claus Jönsson (1961). Fotones, átomos y moléculas siguen una evolución similar.