Expansión térmica

La expansión térmica es la tendencia de la materia a cambiar su forma, área, volumen y densidad en respuesta a un cambio de temperatura, generalmente sin incluir transiciones de fase.
La temperatura es una función monótona de la energía cinética molecular promedio de una sustancia. Cuando una sustancia se calienta, las moléculas comienzan a vibrar y moverse más, creando generalmente más distancia entre ellas. Las sustancias que se contraen al aumentar la temperatura son inusuales y solo ocurren dentro de rangos de temperatura limitados (ver ejemplos a continuación).
La expansión relativa (también llamada deformación) dividida por el cambio de temperatura se denomina coeficiente de expansión térmica lineal del material y generalmente varía con la temperatura. A medida que aumenta la energía en las partículas, comienzan a moverse cada vez más rápido, debilitando las fuerzas intermoleculares entre ellas y, por lo tanto, expandiendo la sustancia.
Predicción
Si hay disponible una ecuación de estado, se puede utilizar para predecir los valores de la expansión térmica en todas las temperaturas y presiones requeridas, junto con muchas otras funciones de estado.
Efectos de contracción (positivos)
Varios materiales se contraen al calentarse dentro de ciertos rangos de temperatura; esto suele denominarse expansión térmica negativa, en lugar de "contracción térmica". Por ejemplo, el coeficiente de expansión térmica del agua cae a cero cuando se enfría a 3,983 °C y luego se vuelve negativo por debajo de esta temperatura; esto significa que el agua tiene una densidad máxima a esta temperatura, y esto lleva a que los cuerpos de agua mantengan esta temperatura en sus profundidades más bajas durante períodos prolongados de clima bajo cero.
También se sabe que otros materiales presentan expansión térmica negativa. El silicio bastante puro tiene un coeficiente de expansión térmica negativo para temperaturas entre 18 y 120 kelvin. ALLVAR Alloy 30, una aleación de titanio, exhibe una expansión térmica negativa anisotrópica en un amplio rango de temperaturas.
Factores
A diferencia de los gases o líquidos, los materiales sólidos tienden a mantener su forma cuando sufren expansión térmica.
La expansión térmica generalmente disminuye al aumentar la energía de enlace, lo que también tiene un efecto en el punto de fusión de los sólidos, por lo que es más probable que los materiales con un punto de fusión alto tengan una menor expansión térmica. En general, los líquidos se expanden ligeramente más que los sólidos. La expansión térmica de los vidrios es ligeramente mayor en comparación con la de los cristales. A la temperatura de transición vítrea, los reordenamientos que ocurren en un material amorfo conducen a discontinuidades características del coeficiente de expansión térmica y del calor específico. Estas discontinuidades permiten la detección de la temperatura de transición vítrea donde un líquido sobreenfriado se transforma en vidrio. Una interesante solución de "refrigeración por calefacción" El efecto ocurre cuando un líquido formador de vidrio se calienta desde el exterior, lo que resulta en una caída de temperatura en el interior del líquido.
La absorción o desorción de agua (u otros disolventes) puede cambiar el tamaño de muchos materiales comunes; Muchos materiales orgánicos cambian de tamaño mucho más debido a este efecto que a la expansión térmica. Los plásticos comunes expuestos al agua pueden, a largo plazo, expandirse en muchos por ciento.
Efecto sobre la densidad
La expansión térmica cambia el espacio entre las partículas de una sustancia, lo que cambia el volumen de la sustancia mientras cambia de manera insignificante su masa (la cantidad insignificante proviene de la equivalencia masa-energía), cambiando así su densidad, lo que tiene un efecto sobre cualquier flotador. fuerzas que actúan sobre él. Esto juega un papel crucial en la convección de masas de fluidos calentadas de manera desigual, lo que hace que la expansión térmica sea en parte responsable del viento y las corrientes oceánicas.
Coeficientes
El coeficiente de expansión térmica describe cómo cambia el tamaño de un objeto con un cambio de temperatura. Específicamente, mide el cambio fraccionario de tamaño por grado de cambio de temperatura a una presión constante, de modo que coeficientes más bajos describen una menor propensión al cambio de tamaño. Se han desarrollado varios tipos de coeficientes: volumétricos, de área y lineales. La elección del coeficiente depende de la aplicación particular y de las dimensiones que se consideran importantes. En el caso de los sólidos, es posible que sólo nos importe el cambio a lo largo de una longitud o de un área determinada.
El coeficiente de expansión térmica volumétrica es el coeficiente de expansión térmica más básico y el más relevante para fluidos. En general, las sustancias se expanden o contraen cuando cambia su temperatura, y la expansión o contracción ocurre en todas direcciones. Las sustancias que se expanden al mismo ritmo en todas direcciones se llaman isotrópicas. Para materiales isotrópicos, el área y el coeficiente de expansión térmica volumétrica son, respectivamente, aproximadamente dos y tres veces mayores que el coeficiente de expansión térmica lineal.
En el caso general de un gas, líquido o sólido, el coeficiente volumétrico de expansión térmica viene dado por
El subíndice "p" a la derivada indica que la presión se mantiene constante durante la expansión, y el subíndice V enfatiza que es la expansión volumétrica (no lineal) la que entra en esta definición general. En el caso de un gas, el hecho de que la presión se mantenga constante es importante, porque el volumen de un gas variará apreciablemente tanto con la presión como con la temperatura. Para un gas de baja densidad, esto se puede deducir de la ley de los gases ideales.
Para diversos materiales

Esta sección resume los coeficientes para algunos materiales comunes.
Para materiales isotrópicos, los coeficientes de expansión térmica lineal α y expansión térmica volumétrica αV están relacionados por αV = 3α. Para los líquidos normalmente se indica el coeficiente de expansión volumétrica y aquí se calcula la expansión lineal para comparar.
Para materiales comunes como muchos metales y compuestos, el coeficiente de expansión térmica es inversamente proporcional al punto de fusión. En particular, para los metales la relación es:
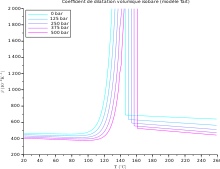
En la siguiente tabla, el rango para α es de 10−7 K−1 para sólidos duros a 10− 3 K−1 para líquidos orgánicos. El coeficiente α varía con la temperatura y algunos materiales tienen una variación muy alta; véase, por ejemplo, la variación frente a la temperatura del coeficiente volumétrico para un polipropileno semicristalino (PP) a diferente presión, y la variación del coeficiente lineal frente a la temperatura para algunos grados de acero (de abajo hacia arriba: acero inoxidable ferrítico, acero inoxidable martensítico , acero al carbono, acero inoxidable dúplex, acero austenítico). El coeficiente lineal más alto en un sólido se ha informado para una aleación de Ti-Nb.
(La fórmula αV ≈ 3α se usa generalmente para sólidos. )
| Material | Tipo de material | Linear coeficiente CLTE α a 20 °C (x10−6 K−1) | Volumen coeficiente αV a 20 °C (x10−6 K−1) | Notas |
|---|---|---|---|---|
| Aluminio | Metal | 23.1 | 69 | |
| Brass | Aleación de metal | 19 | 57 | |
| Carbono de acero | Aleación de metal | 10.8 | 32.4 | |
| CFRP | -0.8 | Anisotropic | Dirección de fibra | |
| Concreto | Aggregate | 12 | 36 | |
| Copper | Metal | 17 | 51 | |
| Diamante | No total | 1 | 3 | |
| Ethanol | Liquid | 250 | 750 | |
| Gasolina | Liquid | 317 | 950 | |
| Cristal | Cristal | 8,5 | 25,5 | |
| Cristal Borosilicate | Cristal | 3.3 | 9.9 | socio de sellado emparejado para tungsteno, molibdeno y kovar. |
| Glycerine | Liquid | 485 | ||
| Oro | Metal | 14 | 42 | |
| Granito | Rock | 35 a 43 | 105–129 | |
| Hielo | No total | 51 | ||
| Invar | 1.2 | 3.6 | ||
| Iron | Metal | 11.8 | 35,4 | |
| Kapton | 20 | 60 | DuPont Kapton 200EN | |
| Lead | Metal | 29 | 87 | |
| Macor | 9.3 | |||
| Nickel | Metal | 13 | 39 | |
| Roble | Biológica | 54 | Perpendicular al grano | |
| Douglas-fir | Biológica | 27 | 75 | radial |
| Douglas-fir | Biológica | 45 | 75 | tangencial |
| Douglas-fir | Biológica | 3.5 | 75 | paralelo al grano |
| Platino | Metal | 9 | 27 | |
| Polipropileno (PP) | Polímero | 150 | 450 | |
| PVC | Polímero | 52 | 156 | |
| Cuarzo fundido | No total | 0,59 | 1.77 | |
| alpha-Quartz | No total | 12–16/6–9 | Paralela a un eje/c-axis T = –50 a 150 °C | |
| Rubber | Biológica | disputadas | disputadas | Ver Talk |
| Rocksalt | Rock | 40 | 120 | |
| Sapphire | No total | 5.3 | Paralel a eje C, o [001] | |
| Carburo de silicona | No total | 2.77 | 8.31 | |
| Silicon | No total | 2.56 | 9 | |
| Plata | Metal | 18 | 54 | |
| "Sitall" | Vitrocerámica | 0,15 | 0±0.45 | promedio de −60 °C a 60 °C |
| Acero inoxidable | Aleación de metal | 10.1 ~ 17.3 | 30.3 ~ 51.9 | |
| Acero | Aleación de metal | 11.0 ~ 13.0 | 33.0 ~ 39.0 | Depende de la composición |
| Titanio | Metal | 8.6 | 26 | |
| Tungsten | Metal | 4.5 | 13.5 | |
| Agua | No total | 69 | 207 | |
| "Zerodur" | Vitrocerámica | ■0.007–0.1 | de 0 °C a 50 °C | |
| Aleación ALLVAR 30 | Aleación de metal | −30 | anisotropic | muestra una expansión térmica negativa en una amplia gama de temperaturas |
En sólidos
Al calcular la expansión térmica es necesario considerar si el cuerpo puede expandirse libremente o si está restringido. Si el cuerpo puede expandirse libremente, la expansión o deformación resultante de un aumento de temperatura se puede calcular simplemente utilizando el coeficiente de expansión térmica aplicable.
Si el cuerpo está restringido de modo que no puede expandirse, entonces la tensión interna será causada (o modificada) por un cambio de temperatura. Esta tensión se puede calcular considerando la deformación que se produciría si el cuerpo fuera libre de expandirse y la tensión necesaria para reducir esa deformación a cero, a través de la relación tensión/deformación caracterizada por el módulo elástico o de Young. En el caso especial de materiales sólidos, la presión ambiental externa no suele afectar apreciablemente el tamaño de un objeto y, por lo tanto, no suele ser necesario considerar el efecto de los cambios de presión.
Los sólidos de ingeniería comunes generalmente tienen coeficientes de expansión térmica que no varían significativamente en el rango de temperaturas para el que están diseñados para ser utilizados, por lo que cuando no se requiere una precisión extremadamente alta, los cálculos prácticos pueden basarse en un promedio constante. valor del coeficiente de expansión.
Longitud

La expansión lineal significa un cambio en una dimensión (longitud) en contraposición al cambio en el volumen (expansión volumétrica). En una primera aproximación, el cambio en las medidas de longitud de un objeto debido a la expansión térmica está relacionado con el cambio de temperatura mediante un coeficiente de expansión térmica lineal (CLTE). Es el cambio fraccionario de longitud por grado de cambio de temperatura. Suponiendo que el efecto de la presión sea insignificante, se puede escribir:
Se puede estimar que el cambio en la dimensión lineal es:
Esta estimación funciona bien mientras el coeficiente de expansión lineal no cambie mucho sobre el cambio de temperatura Δ Δ T{displaystyle Delta T}, y el cambio fraccional de longitud es pequeño Δ Δ L/L≪ ≪ 1{displaystyle Delta L/Lll 1}. Si cualquiera de estas condiciones no mantiene, la ecuación diferencial exacta (utilizando dL/dT{displaystyle mathrm {d} L/mathrm {d} T}) debe ser integrado.
Efectos sobre la tensión
Para materiales sólidos con una longitud significativa, como varillas o cables, una estimación de la cantidad de expansión térmica puede ser descrita por la cepa material, dada por ε ε thermal{displaystyle varepsilon _{mathrm {thermal}} y definido como:
Donde Linitial{displaystyle L_{mathrm {inicial} es la longitud antes del cambio de temperatura y Lfinal{displaystyle L_{mathrm {final} es la longitud después del cambio de temperatura.
Para la mayoría de los sólidos, la expansión térmica es proporcional al cambio de temperatura:
Área
El coeficiente de expansión térmica del área relaciona el cambio en las dimensiones del área de un material con un cambio de temperatura. Es el cambio fraccionario de área por grado de cambio de temperatura. Haciendo caso omiso de la presión, se puede escribir:
El cambio en el área se puede estimar como:
Esta ecuación funciona bien mientras el coeficiente de expansión de área no cambie mucho sobre el cambio de temperatura Δ Δ T{displaystyle Delta T}, y el cambio fraccional en la zona es pequeño Δ Δ A/A≪ ≪ 1{displaystyle Delta A/All 1}. Si cualquiera de estas condiciones no se mantiene, la ecuación debe ser integrada.
Volumen
Para un sólido, se pueden ignorar los efectos de la presión sobre el material y el coeficiente de expansión térmica volumétrica (o cúbica) se puede escribir:
Esto significa que el volumen de un material cambia en una cantidad fraccionaria fija. Por ejemplo, un bloque de acero con un volumen de 1 metro cúbico podría expandirse a 1,002 metros cúbicos cuando la temperatura aumenta 50 K. Esta es una expansión del 0,2%. Si un bloque de acero tiene un volumen de 2 metros cúbicos, entonces, en las mismas condiciones, se expandiría a 2,004 metros cúbicos, nuevamente una expansión del 0,2%. El coeficiente de expansión volumétrica sería del 0,2 % para 50 K, o del 0,004 % K−1.
Si se conoce el coeficiente de expansión, se puede calcular el cambio de volumen
El ejemplo anterior supone que el coeficiente de expansión no cambió a medida que cambió la temperatura y que el aumento de volumen es pequeño en comparación con el volumen original. Esto no siempre es cierto, pero para pequeños cambios de temperatura es una buena aproximación. Si el coeficiente de expansión volumétrica cambia apreciablemente con la temperatura, o el aumento de volumen es significativo, entonces será necesario integrar la ecuación anterior:
Materiales Isotropic
Para materiales isotrópicos el coeficiente de expansión térmica volumétrica es tres veces el coeficiente lineal:
Esta proporción surge porque el volumen se compone de tres direcciones ortogonales mutuamente. Así, en un material isotrópico, para pequeños cambios diferenciales, un tercio de la expansión volumétrica está en un solo eje. Como ejemplo, tomar un cubo de acero que tiene lados de longitud L. El volumen original será V=L3{displaystyle V=L^{3} y el nuevo volumen, después de un aumento de temperatura, será
Podemos ignorar fácilmente los términos ya que ΔL es una cantidad pequeña que al elevar al cuadrado se vuelve mucho más pequeña y al elevar al cubo se vuelve aún más pequeña.
Así que
La aproximación anterior sostiene para pequeños cambios de temperatura y dimensiones (es decir, cuando Δ Δ T{displaystyle Delta T} y Δ Δ L{displaystyle Delta L} son pequeños), pero no se sostiene si se trata de ir y salir entre los coeficientes volumétricos y lineales utilizando valores más grandes de Δ Δ T{displaystyle Delta T}. En este caso, debe tenerse en cuenta el tercer mandato (y a veces incluso el cuarto mandato) en la expresión anterior.
De manera similar, el coeficiente de expansión térmica del área es dos veces el coeficiente lineal:
Esta relación se puede encontrar de una manera similar a la anterior en el ejemplo lineal, señalando que el área de una cara en el cubo es simplemente L2{displaystyle L^{2}. Asimismo, se deben tener en cuenta las mismas consideraciones al tratar con grandes valores de Δ Δ T{displaystyle Delta T}.
Dicho de manera más simple, si la longitud de un sólido cúbico se expande de 1,00 m a 1,01 m, entonces el área de uno de sus lados se expande de 1,00 m2 a 1,02 m2 y su volumen se expande desde 1,00 m3 hasta 1,03 m3.
Materiales anisotrópicos
Materiales con estructuras anisotrópicas, como cristales (con menos simetría cúbica, por ejemplo fases martensiáticas) y muchos compuestos, generalmente tendrán diferentes coeficientes de expansión lineal α α L{displaystyle alpha ¿Qué? en diferentes direcciones. Como resultado, la expansión volumétrica total se distribuye desigualmente entre los tres ejes. Si la simetría cristalina es monoclínica o triclínica, incluso los ángulos entre estos ejes están sujetos a cambios térmicos. En tales casos es necesario tratar el coeficiente de expansión térmica como un tensor con hasta seis elementos independientes. Una buena manera de determinar los elementos del tensor es estudiar la expansión por la difusión de polvo de rayos X. El tensor de coeficiente de expansión térmica para los materiales que poseen simetría cúbica (por ejemplo, FCC, BCC) es isotrópico.
Dependencia de la temperatura
Los coeficientes de expansión térmica de los sólidos generalmente muestran poca dependencia de la temperatura (excepto a temperaturas muy bajas), mientras que los líquidos pueden expandirse a diferentes velocidades a diferentes temperaturas. Hay algunas excepciones: por ejemplo, el nitruro de boro cúbico exhibe una variación significativa de su coeficiente de expansión térmica en un amplio rango de temperaturas. Otro ejemplo es la parafina que en su forma sólida tiene un coeficiente de expansión térmica que depende de la temperatura.
En gases
Puesto que los gases llenan la totalidad del contenedor que ocupan, el coeficiente de expansión térmica volumétrica a presión constante, α α V{displaystyle alpha _{V}, es el único de interés.
Para un gas ideal, una fórmula se puede obtener fácilmente por la diferenciación de la ley de gas ideal, pVm=RT{displaystyle PV_{m}=RT}. Este rendimiento
Para una expansión térmica isobarica, dp=0{displaystyle mathrm {d} p=0}Así que pdVm=RdT{displaystyle pmathrm {d} V_{m}=Rmathrm {d} T} y el coeficiente de expansión térmica isobaric es:
Computación cero absoluta

De 1787 a 1802, Jacques Charles (inédito), John Dalton y Joseph Louis Gay-Lussac determinaron que, a presión constante, los gases ideales expandían o contraían su volumen linealmente (ley de Charles) por aproximadamente 1/273 partes por grado Celsius de cambio de temperatura hacia arriba o hacia abajo, entre 0° y 100 °C. Esto sugirió que el volumen de un gas enfriado a aproximadamente -273 °C llegaría a cero.
En octubre de 1848, William Thomson, un profesor de Filosofía Natural de 24 años en la Universidad de Glasgow, publicó el artículo En una escala termométrica absoluta.
En una nota a pie de página, Thomson calculó que el "frío infinito" (cero absoluto) equivalía a −273 °C (llamó a la temperatura en °C la "temperatura de los termómetros de aire" de la época). Este valor de "−273" Se consideró la temperatura a la cual el volumen del gas ideal llega a cero. Al considerar una expansión térmica lineal con la temperatura (es decir, un coeficiente de expansión térmica constante), el valor del cero absoluto se extrapoló linealmente como el recíproco negativo de 0,366/100 °C: el coeficiente promedio aceptado de expansión térmica de un gas ideal en el intervalo de temperatura de 0 a 100 °C, lo que da una consistencia notable al valor actualmente aceptado de −273,15 °C.
En líquidos
La expansión térmica de los líquidos suele ser mayor que la de los sólidos porque las fuerzas intermoleculares presentes en los líquidos son relativamente débiles y las moléculas que los constituyen son más móviles. A diferencia de los sólidos, los líquidos no tienen forma definida y toman la forma del recipiente. En consecuencia, los líquidos no tienen una longitud ni un área definidas, por lo que las expansiones lineales y regionales de los líquidos solo tienen importancia porque pueden aplicarse a temas como la termometría y las estimaciones del aumento del nivel del mar debido al cambio climático global. A veces, αL todavía se calcula a partir del valor experimental de αV.
En general, los líquidos se expanden al calentarlos, excepto el agua fría; por debajo de 4 °C se contrae, lo que lleva a un coeficiente de expansión térmica negativo. A temperaturas más altas muestra un comportamiento más típico, con un coeficiente de expansión térmica positivo.
Aparente y absoluta
La expansión de los líquidos generalmente se mide en un recipiente. Cuando un líquido se expande en un recipiente, el recipiente se expande junto con el líquido. Por lo tanto, el aumento de volumen observado (medido por el nivel del líquido) no es el aumento real de su volumen. La expansión del líquido con respecto al recipiente se llama expansión aparente, mientras que la expansión real del líquido se llama expansión real o expansión absoluta. . La relación entre el aumento aparente de volumen del líquido por unidad de aumento de temperatura y el volumen original se denomina coeficiente de expansión aparente. La expansión absoluta se puede medir mediante diversas técnicas, incluidos los métodos ultrasónicos.
Históricamente, este fenómeno complicó la determinación experimental de los coeficientes de expansión térmica de los líquidos, ya que una medición directa del cambio de altura de una columna de líquido generada por la expansión térmica es una medida de la expansión aparente del líquido. Así, el experimento mide simultáneamente dos coeficientes de expansión y la medición de la expansión de un líquido debe tener en cuenta también la expansión del recipiente. Por ejemplo, cuando un matraz con un vástago largo y estrecho, que contiene suficiente líquido para llenar parcialmente el vástago, se coloca en un baño térmico, la altura de la columna de líquido en el vástago inicialmente disminuirá, seguida inmediatamente por un aumento de esa altura. hasta que todo el sistema de matraz, líquido y baño térmico se haya calentado por completo. La caída inicial en la altura de la columna de líquido no se debe a una contracción inicial del líquido, sino más bien a la expansión del matraz cuando entra en contacto primero con el baño térmico.
Poco después, el líquido del matraz se calienta por el propio matraz y comienza a expandirse. Dado que los líquidos suelen tener un porcentaje de expansión mayor que los sólidos para el mismo cambio de temperatura, la expansión del líquido en el matraz eventualmente excede la del matraz, lo que hace que el nivel de líquido en el matraz aumente. Para aumentos de temperatura pequeños e iguales, el aumento de volumen (expansión real) de un líquido es igual a la suma del aumento aparente de volumen (expansión aparente) del líquido y el aumento de volumen del recipiente que lo contiene. La expansión absoluta del líquido es la expansión aparente corregida por la expansión del recipiente que lo contiene.
Ejemplos y aplicaciones

Se debe considerar la expansión y contracción de los materiales al diseñar estructuras grandes, al usar cinta o cadena para medir distancias en estudios topográficos, al diseñar moldes para fundir material caliente y en otras aplicaciones de ingeniería cuando se producen grandes cambios en las dimensiones debido a Se esperan temperaturas
La expansión térmica también se utiliza en aplicaciones mecánicas para encajar piezas unas sobre otras, p. Se puede colocar un casquillo sobre un eje haciendo que su diámetro interior sea ligeramente más pequeño que el diámetro del eje, luego calentándolo hasta que encaje sobre el eje y dejándolo enfriar después de haberlo empujado sobre el eje, logrando así un & #39;ajuste por contracción'. El ajuste por contracción por inducción es un método industrial común para precalentar componentes metálicos entre 150 °C y 300 °C, lo que hace que se expandan y permita la inserción o extracción de otro componente.
Existen algunas aleaciones con un coeficiente de expansión lineal muy pequeño, utilizadas en aplicaciones que exigen cambios muy pequeños en la dimensión física en un rango de temperaturas. Uno de ellos es Invar 36, con una expansión aproximadamente igual a 0,6×10−6 K−1. Estas aleaciones son útiles en aplicaciones aeroespaciales donde pueden ocurrir grandes cambios de temperatura.
El aparato de Pullinger se utiliza para determinar la expansión lineal de una varilla metálica en el laboratorio. El aparato consta de un cilindro metálico cerrado en ambos extremos (llamado una chaqueta de vapor). Se proporciona una entrada y salida para el vapor. El vapor para calentar la varilla es suministrado por una caldera que está conectada por un tubo de goma a la entrada. El centro del cilindro contiene un agujero para insertar un termómetro. La vara bajo investigación está encerrada en una chaqueta de vapor. Uno de sus extremos es libre, pero el otro extremo está presionado contra un tornillo fijo. La posición de la varilla está determinada por un medidor de tornillo o esferómetro.
Para determinar el coeficiente de expansión térmica lineal de un metal, se calienta un tubo hecho de ese metal haciendo pasar vapor a través de él. Un extremo del tubo está fijado de forma segura y el otro descansa sobre un eje giratorio, cuyo movimiento se indica mediante un puntero. Un termómetro adecuado registra la temperatura de la tubería. Esto permite calcular el cambio relativo de longitud por grado de cambio de temperatura.

El control de la expansión térmica en materiales frágiles es una preocupación clave por una amplia variedad de razones. Por ejemplo, tanto el vidrio como la cerámica son frágiles y la temperatura desigual provoca una expansión desigual, lo que a su vez provoca estrés térmico y esto podría provocar fracturas. La cerámica debe unirse o trabajar en conjunto con una amplia gama de materiales y, por lo tanto, su expansión debe adaptarse a la aplicación. Debido a que los esmaltes deben estar firmemente adheridos a la porcelana subyacente (u otro tipo de cuerpo), su expansión térmica debe ajustarse para "encajar" en la superficie. el cuerpo para que no se produzcan enloquecimientos o escalofríos. Un buen ejemplo de productos cuya expansión térmica es la clave de su éxito son CorningWare y la bujía. La expansión térmica de los cuerpos cerámicos se puede controlar mediante cocción para crear especies cristalinas que influirán en la expansión general del material en la dirección deseada. Además o en su lugar, la formulación del cuerpo puede emplear materiales que proporcionen partículas de la expansión deseada a la matriz. La expansión térmica de los esmaltes está controlada por su composición química y el calendario de cocción al que fueron sometidos. En la mayoría de los casos, existen cuestiones complejas relacionadas con el control de la expansión del cuerpo y del esmalte, por lo que el ajuste de la expansión térmica debe realizarse teniendo en cuenta otras propiedades que se verán afectadas y, en general, es necesario hacer concesiones.
La expansión térmica puede tener un efecto notable en la gasolina almacenada en tanques de almacenamiento sobre el suelo, lo que puede hacer que las bombas de gasolina dispensen gasolina que puede estar más comprimida que la gasolina almacenada en tanques de almacenamiento subterráneos en invierno, o menos comprimida que la gasolina almacenada en tanques de almacenamiento subterráneos en verano.

La expansión inducida por el calor debe tenerse en cuenta en la mayoría de las áreas de la ingeniería. Algunos ejemplos son:
- Las ventanas metálicas necesitan espaciadores de goma.
- Los neumáticos de goma deben realizar bien sobre una gama de temperaturas, siendo pasivamente calentados o refrigerados por superficies de carretera y clima, y fuertemente calentados por flexión mecánica y fricción.
- Las tuberías de calefacción de agua caliente de metal no deben utilizarse en largas longitudes rectas.
- Grandes estructuras como los ferrocarriles y puentes necesitan articulaciones de expansión en las estructuras para evitar el golpe de sol.
- Un péndulo de cuadrícula utiliza un arreglo de diferentes metales para mantener una longitud péndulo más estable de temperatura.
- Una línea de poder en un día caliente es droopy, pero en un día frío es apretado. Esto es porque los metales se expanden bajo calor.
- Las juntas de expansión absorben la expansión térmica en un sistema de tuberías.
- La ingeniería de precisión casi siempre requiere que el ingeniero preste atención a la expansión térmica del producto. Por ejemplo, cuando se utiliza un microscopio electrónico de escaneo pequeños cambios en la temperatura, como 1 grado, puede hacer que una muestra cambie su posición relativa al punto de foco.
- Los termómetros líquidos contienen un líquido (generalmente mercurio o alcohol) en un tubo, que lo limita a fluir en una sola dirección cuando su volumen se expande debido a los cambios de temperatura.
- Un termómetro mecánico bimetálico utiliza una tira bimetállica y curvas debido a la diferente expansión térmica de los dos metales.
Contenido relacionado
Julio (unidad)
Pascal (unidad)
Precisión y exactitud


















































