Excentricidad (matemáticas)

En matemáticas, la excentricidad de una sección cónica es un número real no negativo que caracteriza de forma única su forma.

Se puede pensar en la excentricidad como una medida de cuánto se desvía una sección cónica de ser circular. En particular:

• La excentricidad de un círculo es 0.
• La excentricidad de una elipse que no es un círculo es entre 0 y 1.
• La excentricidad de una parabola es 1.
• La excentricidad de una hiperbola es mayor que 1.
• La excentricidad de un par de líneas es ${\displaystyle \infty }$

Dos secciones cónicas con la misma excentricidad son similares.

Definiciones

Cualquier sección cónica se puede definir como el lugar geométrico de puntos cuyas distancias a un punto (el foco) y a una línea (la directriz) están en una proporción constante. Esa relación se llama excentricidad, comúnmente denotada como e.

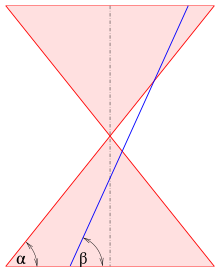
La excentricidad también se puede definir en términos de la intersección de un plano y un cono de doble pelo asociado con la sección cónica. Si el cono está orientado con su eje vertical, la excentricidad es

${\displaystyle e={\frac\sin \beta }{\sin \alpha },\\\\\\\\c\c\c\cH0} 0 0 0 0 0 0 0 \beta \leq 90^{\circ }$

donde β es el ángulo entre el plano y el horizontal y el α es el ángulo entre el generador de inclinación del cono y el horizontal. Para ${\displaystyle \beta =0}$ la sección del avión es un círculo, para ${\displaystyle \beta =\alpha }$ una parabola. (El avión no debe encontrarse con el vértice del cono.)

El excentricidad lineal de un elipse o hiperbola, denotado c (o a veces f o e), es la distancia entre su centro y cualquiera de sus dos focos. La excentricidad se puede definir como la relación de la excentricidad lineal con el eje semimajor aEs decir, ${\displaystyle e={\frac {c}{a}}$ (La falta de un centro, la excentricidad lineal para el parabolas no está definida). Cabe señalar que una parabola puede tratarse como un elipse o una hiperbola, pero con un punto focal en el infinito.

Nombres alternativos

La excentricidad a veces se denomina primera excentricidad para distinguirla de la segunda excentricidad y la tercera excentricidad definidas para elipses (ver más abajo). La excentricidad también se denomina a veces excentricidad numérica.

En el caso de elipses e hipérbolas, la excentricidad lineal a veces se denomina separación semifocal.

Notación

Se utilizan tres convenciones de notación:

1. e para la excentricidad y c para la excentricidad lineal.
2. ε para la excentricidad y e para la excentricidad lineal.
3. e o ε c) para la excentricidad y f para la excentricidad lineal (mnemónica para la mitad-focal separation).

Este artículo utiliza la primera notación.

Valores

Sección cónica	Ecuación	Eccentricity (Eccentricity)e)	Excentricidad lineal (excentricidad lineal)c)
Circle	${\displaystyle ¿Qué?$	${\displaystyle 0}$	${\displaystyle 0}$
Ellipse	${\fnMicroc} {x^{2}{a^{2}}+{\frac} {\fnK} {\cHFF}}}=1}$ o ${\fnMicroc} {y} {\fn} {\fnMicroc}}} {\fnMicroc}}} {\f}}} {\\fn}}}}} {\fn}}} {\f}}}} {\fnMicroc}} {x^{2}{b^{2}}=1}$ Donde ${\displaystyle a prendab}$	${\displaystyle {\sqrt {1-{\frac {\fn}}}} {\fn}}}} {\fn}}}}} {\f}}}}}}}}}}}}}}}}}}} {\c}}} {}}}}}}}}}}} {}}}}}}}}} {}}}}}}}} {}}}}}}}}}}}}} {}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}} {}}}}}}}}}}}}}}}}}}} {}}}}}}}}}}}}}}}}}}}}}}}}} {}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}$	${\displaystyle {\sqrt {2}-b}}}$
Parabola	${\displaystyle x^{2}=4ay}$	${\displaystyle 1}$	indefinidos (${\displaystyle \infty }$)
Hyperbola	${\displaystyle {\frac {x^{2}{a^{2}}-{\frac} {y} {y}{b^{2}}=1}$ o ${\displaystyle {\frac {\fnK} {\f}} {\f} {\fnK}} {\f} {\f}} {\f}}} {\f}\f}} {x^{2}{b^{2}}=1}$	${\fnMicroc} {\fn}}}} {\fn}}}} {\fn}}}}} {\f}}}}}}}}}}}}}}}}}}} {\c}}} {}}}}}}}}}}} {}}}}}}}}} {}}}}}}}} {}}}}}}}}}}}}} {}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}} {}}}}}}}}}}}}}}}}}}} {}}}}}}}}}}}}}}}}}}}}}}}}} {}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}$	${\displaystyle {\sqrt {\c}+b^{2}}}}$

Aquí, para la elipse y la hipérbola, a es la longitud del semieje mayor y b es la longitud del semieje menor.

Cuando la sección cónica se da en la forma cuadrática general

${\displaystyle Ax^{2}+Bxy+Cy^{2}+Dx+Ey+F=0,}$

la siguiente fórmula da la excentricidad e si la sección cónica no es una parábola (que tiene una excentricidad igual a 1), ni una hipérbola degenerada ni una elipse degenerada, ni una elipse imaginaria:

${\fnMicroc} {2} {\sqrt {\cH00}}{2}}{\eta (A+C)+{\sqrt {}}}}}}}}}}}}}}}$

Donde ${\displaystyle \eta =1}$ si el determinante de la matriz 3×3

${\displaystyle {\begin{bmatrix}A tendrían una relación entre dos personas y dos, tres, tres, tres, tres, tres, tres, tres, tres, tres, tres, tres, tres, tres, tres, tres, tres, tres, tres, tres, tres, tres, tres, tres, tres, tres, tres, tres, tres, tres, tres, tres, tres, tres, tres, tres, tres.$

es negativo o ${\displaystyle \eta =-1}$ si ese determinante es positivo.

Elipses

La excentricidad de una elipse es estrictamente menor que 1. Cuando los círculos (que tienen excentricidad 0) se cuentan como elipses, la excentricidad de una elipse es mayor o igual a 0; Si a los círculos se les da una categoría especial y se excluyen de la categoría de elipses, entonces la excentricidad de una elipse es estrictamente mayor que 0.

Para cualquier elipse, sea a la longitud de su semieje mayor y b sea la longitud de su semieje menor. En el sistema de coordenadas con origen en el centro de la elipse y eje x alineado con el eje mayor, los puntos en el elipse satisface la ecuación

${\fnMicroc} {x^{2}{a^{2}}+{\frac} {y} {y}{b^{2}}=1,}$

con foci en coordenadas ${\displaystyle (\pm c,0)}$ para ${\textstyle c={\sqrt {a^{2}-b^{2}}}$

Definimos una serie de conceptos adicionales relacionados (solo para elipses):

Nombre	Signatura	en términos de a y b	en términos de e
Primera excentricidad	${\displaystyle e}$	${\displaystyle {\sqrt {1-{\frac {\fn}}}} {\fn}}}} {\fn}}}}} {\f}}}}}}}}}}}}}}}}}}} {\c}}} {}}}}}}}}}}} {}}}}}}}}} {}}}}}}}} {}}}}}}}}}}}}} {}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}} {}}}}}}}}}}}}}}}}}}} {}}}}}}}}}}}}}}}}}}}}}}}}} {}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}$	${\displaystyle e}$
Segunda excentricidad	${\displaystyle e'}$	${\fnMicroc} {\fnK}} {}}}}}} {}}}} {\f}}}} {\f}}}}}}}}} {}}} {}}}}}}} {}}}}}}} {}}}}}}}}}}}}}}}}} {}}}}}}}} {}}}}} {}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}} {}}}}}}}} {}}}}}}}} {}}}}}}}}}}}}}}}}} {}}}}}}}}}}} {}}}}}} {}}}}}}}}}}}}}}}}}} {}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}$	${\displaystyle {\frac {e}{\sqrt {1-e^{2}}}}$
Tercera excentricidad	${\displaystyle e'={\sqrt {m}}$	${\displaystyle {\frac {\sqrt {a^{2}-b^{2}}{\sqrt {}}}}$	${\displaystyle {\frac {e}{\sqrt {2-e^{2}}}}$
Eccentricidad angular	${\displaystyle \alpha }$	${\displaystyle \cos ^{-1}\left({\frac {b}\right)}$	${\displaystyle \sin ^{-1}e}$

Otras fórmulas para la excentricidad de una elipse

La excentricidad de una elipse es, más simplemente, la relación de la excentricidad lineal c (distancia entre el centro de la elipse elipse y cada foco) a la longitud del semieje mayor a.

${\displaystyle e={\frac {c}{a}}$

La excentricidad es también la relación entre el semieje mayor a y la distancia d desde el centro hasta la directriz:

${\displaystyle e={\frac {a}{d}.}$

La excentricidad se puede expresar en términos de aplanamiento f (definido como ${\displaystyle f=1-b/a$ para el eje semimajor a y semiminor axis b):

${\displaystyle e={\sqrt {1-(1-f)}={\sqrt {f(2-f)}}}$

(El aplanamiento puede indicarse con g en algunas áreas temáticas si f es excentricidad lineal).

Defina el radio máximo y mínimo ${\displaystyle r_{\text{max}}$ y ${\displaystyle ¿Qué?$ como las distancias máximas y mínimas de enfocarse a la elipse (es decir, las distancias de enfocarse a los dos extremos del eje principal). Luego con eje semimajor a, la excentricidad es dada por

${\displaystyle e={\frac {\fnh\fnh} {\fnh00}} {\fnh\fnh00}}}} {\f}}}}= {\frac}} {\f}}}}} {\fnK}}}} {\f}}}}}}} {\fn\f}}}}}}}}}} {\m\f}}}}}} {\f}}}}}}} {\f}}}}}}} {\f}}}}}}}}}}}} {\f}}}}}} {\f} {\f}}}}}} {\f}}}}}}}}}}}}}}}}}}}}}}} {\f} {\f}}}}} {\f}}}}} {\\\\\\\\f}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}} {\f}}}}}} {\fnK}} {\fnK}} {\fnK}}}} {\fnK}}}}$

que es la distancia entre los focos dividida por la longitud del eje mayor.

Hiperbolas

La excentricidad de una hiperbola puede ser cualquier número real superior a 1, sin límite superior. La excentricidad de una hiperbola rectangular es ${\displaystyle {\sqrt {2}}$.

Cuádricas

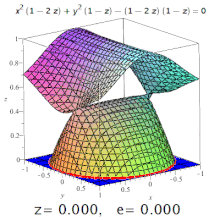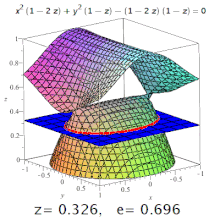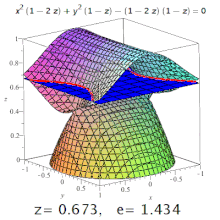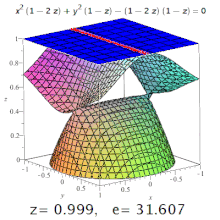
La excentricidad de una cuádrica tridimensional es la excentricidad de una sección designada de la misma. Por ejemplo, en un elipsoide triaxial, la excentricidad meridional es la de la elipse formada por una sección que contiene tanto el eje más largo como el más corto (uno de los cuales será el eje polar), y la excentricidad ecuatorial es la excentricidad de la elipse formada por una sección que pasa por el centro, perpendicular al eje polar (es decir, en el plano ecuatorial). Pero: las secciones cónicas también pueden aparecer en superficies de orden superior (ver imagen).

Mecánica celestial

En la mecánica celestial, para órbitas encuadradas en un potencial esférico, la definición anterior se generaliza informalmente. Cuando la distancia del apocentro está cerca de la distancia del pericenter, se dice que la órbita tiene baja excentricidad; cuando son muy diferentes, se dice que la órbita es excéntrica o tiene excentricidad cerca de la unidad. Esta definición coincide con la definición matemática de excentricidad para elipses, en Keplerian, es decir, ${\displaystyle 1/r}$ potenciales.

Clasificaciones análogas

Varias clasificaciones en matemáticas utilizan terminología derivada de la clasificación de secciones cónicas por excentricidad:

• Clasificación de elementos de SL2(R) como elípticos, parabólicos e hiperbólicos, y de manera similar para la clasificación de elementos de PSL₂(R), las transformaciones reales de Möbius.
• Clasificación de distribuciones discretas por ratio de varianza a media; véase acumuladores de algunas distribuciones discretas de probabilidad para obtener detalles.
• Clasificación de ecuaciones diferenciales parciales es por analogía con la clasificación de secciones cónicas; vea ecuaciones diferenciales parciales elípticas, parabólicas e hiperbólicas.