Estrella (juego de mesa)

Star es un juego de mesa de estrategia abstracta para dos jugadores desarrollado por Craige Schensted (ahora Ea Ea). Se publicó por primera vez en la edición de septiembre de 1983 de la revista Games. Es un juego de conexión similar a Hex, Y, Havannah y TwixT. Sin embargo, a diferencia de estos juegos, el resultado se basa en que un jugador obtenga una puntuación final más alta en lugar de lograr un objetivo específico. Desde entonces, ha desarrollado una versión un poco más complicada llamada *Star con un mejor equilibrio entre movimientos de borde y centro, escribiendo "*Star es lo que esos otros juegos querían ser. ."

Reglas del juego

Star se juega en un tablero de celdas hexagonales. Aunque el tablero puede tener cualquier tamaño y forma, generalmente se utiliza un tablero con bordes desiguales para evitar ataduras. Los jugadores no pueden colocar piedras en las celdas del borde hexagonal parcial fuera del borde del tablero; estos se utilizan para anotar. Un jugador coloca piedras negras en el tablero; el otro jugador coloca piedras blancas.

El juego comienza cuando un jugador coloca una piedra en el tablero. Para evitar darle ventaja al primer jugador, se utiliza una regla circular, que permite al segundo jugador cambiar de bando en ese punto. Luego, los jugadores alternan turnos y colocan una piedra en una celda vacía del tablero. Los jugadores pueden pasar; El juego termina cuando ambos jugadores pasan.

Al final del juego los jugadores cuentan sus puntuaciones. Una "estrella" es un grupo de piedras conectadas que pertenecen a un jugador y que tocan al menos tres celdas de borde de hexágono parcial. La puntuación de una estrella es el número de celdas del borde del hexágono parcial que toca menos dos. La puntuación de un jugador es el total de todas las estrellas del color de ese jugador. El jugador con mayor puntuación gana.

Para cualquier tablero, la puntuación final total de los dos jugadores es constante. La puntuación combinada de los dos jugadores es igual al número de celdas del borde del hexágono parcial, menos dos.

Ejemplo

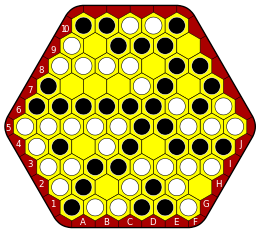
Este tablero de 5×6 tiene 75 celdas en 10 filas (1–10) y 11 columnas (A–J) que tocan 33 celdas de borde de hexágono parcial.

Las blancas tienen cinco estrellas distintas con una puntuación neta total de 14.

1. La célula estrella que toca [A2] se comunica con 6 celdas fronterizas y tiene una puntuación neta de 4 puntos
2. Toque [B1], 8 celdas fronterizas; puntuación neta 6
3. Toque [D8], 3 celdas fronterizas; puntuación neta 1
4. Toque [H10], 3 celdas fronterizas; puntuación neta 1
5. Tocar [J5], 4 celdas fronterizas; puntuación neta 2

Las negras tienen dos estrellas distintas con una puntuación neta total de 17.

1. Tocando [A1], 18 celdas fronterizas; puntuación neta 16
2. Toque [D1], 3 celdas fronterizas; puntuación neta 1

Las negras ganan conectando más eficazmente sus estrellas. Por ejemplo, si la piedra en [D3] fuera blanca, eso conectaría sus dos primeras estrellas y la puntuación neta sería 6+8-2 = 12 en lugar de 10. De la misma manera, esto desconectaría la estrella negra grande, lo que dividirse en dos estrellas, haciendo contacto con 3 y 15 celdas fronterizas, para una puntuación neta de 3+15-4 = 14 en lugar de 16. Aunque este único cambio no habría sido suficiente para que las blancas ganaran, ilustra la recompensa por conectar estrellas. .

Debido a la geometría del tablero, las seis celdas del perímetro de las esquinas [A1], [A5], [F1], [F10], [J5] y [J10] cada una hace contacto con 3 celdas del borde y puntuarían un punto cada uno con una sola piedra ocupante. Schensted consideró que se trataba de una ventaja injusta y propuso un cambio de regla para que estas celdas valieran dos puntos cada una. Esto se puede lograr modificando esas celdas de las esquinas para que tengan cinco lados; La eliminación de las seis pequeñas celdas de puntuación parcial en las esquinas significa que la puntuación total resultante de ambos jugadores es 25 en el tablero de 5×6.

Para el juego de ejemplo ilustrado aquí, la puntuación revisada es Blanco 11, Negro 14 con las esquinas modificadas de 2 puntos. Cada jugador ocupó tres celdas de las esquinas en este ejemplo, por lo que la puntuación se reduce en tres puntos cada uno usando el tablero modificado.

Historia

Schensted desarrolló por primera vez Poly-Y en la década de 1970, una versión más generalizada de Y en la que Y es el caso especial de Poly-Y utilizando una tabla con tres lados y esquinas. A través de la experimentación, Schensted descubrió que lo ideal era un tablero con nueve lados y esquinas y siete elementos por lado; más esquinas significarían lados más cortos, y los jugadores podrían hacer una "Y" tocar tres lados con relativa facilidad.

Después de que R. Wayne Schmittberger se pusiera en contacto con Schensted a principios de la década de 1980 y le pidiera publicar Poly-Y en la revista Games, Schensted desempolvó el concepto y lo probó con su esposa. , Irene. Durante uno de sus juegos, decidieron otorgar una bonificación al jugador que uniera sus grupos de manera más efectiva para evitar empates, lo que dio como resultado las reglas para Estrella.