Estimación de máxima verosimilitud

format_list_bulleted Contenido keyboard_arrow_down

ImprimirCitar

Método de estimación de los parámetros de un modelo estadístico, observaciones dadas

En estadística, la estimación de máxima verosimilitud (MLE) es un método para estimar los parámetros de una distribución de probabilidad supuesta, dados algunos datos observados. Esto se logra maximizando una función de verosimilitud para que, bajo el modelo estadístico asumido, los datos observados sean los más probables. El punto en el espacio de parámetros que maximiza la función de verosimilitud se denomina estimación de máxima verosimilitud. La lógica de máxima verosimilitud es tanto intuitiva como flexible y, como tal, el método se ha convertido en un medio dominante de inferencia estadística.

Si la función de verosimilitud es diferenciable, se puede aplicar la prueba de la derivada para encontrar máximos. En algunos casos, las condiciones de primer orden de la función de verosimilitud pueden resolverse analíticamente; por ejemplo, el estimador de mínimos cuadrados ordinarios para un modelo de regresión lineal maximiza la probabilidad cuando se supone que todos los resultados observados tienen distribuciones normales con la misma varianza.

Desde la perspectiva de la inferencia bayesiana, MLE es generalmente equivalente a la estimación máxima a posteriori (MAP) con distribuciones previas uniformes (o una distribución previa normal con una desviación estándar de infinito). En la inferencia frecuentista, MLE es un caso especial de un estimador extremo, siendo la función objetivo la verosimilitud.

Principios

Modelamos un conjunto de observaciones como muestra aleatoria de una distribución de probabilidad articular desconocida que se expresa en términos de un conjunto de parámetros. El objetivo de la estimación de probabilidad máxima es determinar los parámetros para los cuales los datos observados tienen la mayor probabilidad conjunta. Escribimos los parámetros que rigen la distribución conjunta como vector ${displaystyle ;theta =left[theta _{1},,theta _{2},,ldots,theta _{k}right]^{mathsf {T}};}$ para que esta distribución se encuentre dentro de una familia paramétrica ${displaystyle ;{f(cdot ,;theta)mid theta in Theta };,}$ Donde ${displaystyle ,Theta ,}$ se llama parameter space, un subconjunto finito-dimensional del espacio Euclideano. Evaluar la densidad articular en la muestra de datos observada ${displaystyle ;mathbf {y} =(y_{1},y_{2},ldotsy_{n});}$ da una función de valor real,

{displaystyle {mathcal {L}}_{n}(theta)={mathcal {L}}_{n}(theta;mathbf {y})=f_{n}(mathbf {y};theta);,}

que se llama la función de probabilidad. Para variables aleatorias independientes y distribuidas idénticamente, ${displaystyle f_{n}(mathbf {y};theta)}$ será el producto de las funciones de densidad univariada:

{displaystyle f_{n}(mathbf {y};theta)=prod _{k=1}^{n},f_{k}^{mathsf {univar}}(y_{k};theta)~.}

El objetivo de la estimación de máxima verosimilitud es encontrar los valores de los parámetros del modelo que maximizan la función de verosimilitud en el espacio de parámetros, es decir

{displaystyle {hat {theta }}={underset {theta in Theta }{operatorname {arg;max} }},{mathcal {L}}_{n}(theta ,;mathbf {y})~.}

Intuitivamente, esto selecciona los valores del parámetro que hacen los datos observados más probables. El valor específico ${displaystyle ~{hat {theta }}={hat {theta }}_{n}(mathbf {y})in Theta ~}$ que maximiza la función de probabilidad ${displaystyle ,{mathcal {L}}_{n},}$ se llama la estimación de probabilidad máxima. Además, si la función ${displaystyle ;{hat {theta }}_{n}:mathbb {R} ^{n}to Theta ;}$ así definido es mensurable, entonces se llama el estimador de probabilidad máxima. Es generalmente una función definida sobre el espacio de muestra, es decir, tomar una muestra dada como su argumento. Una condición suficiente pero no necesaria para su existencia es que la función de probabilidad sea continua sobre un espacio de parámetro ${displaystyle ,Theta ,}$ Eso es compacto. Para abrir ${displaystyle ,Theta ,}$ la función de probabilidad puede aumentar sin alcanzar nunca un valor supremum.

En la práctica, a menudo es conveniente trabajar con el logaritmo natural de la función de probabilidad, llamada log-verosimilitud:

{displaystyle ell (theta ,;mathbf {y})=ln {mathcal {L}}_{n}(theta ,;mathbf {y})~.}

Puesto que el logaritmo es una función monotónica, el máximo ${displaystyle ;ell (theta ,;mathbf {y});}$ ocurre al mismo valor $theta$ como lo hace el máximo ${displaystyle ,{mathcal {L}}_{n}~.}$ Si ${displaystyle ell (theta ,;mathbf {y})}$ es diferente en ${displaystyle ,Theta ,,}$ las condiciones necesarias para la ocurrencia de un máximo (o un mínimo)

{displaystyle {frac {partial ell }{partial theta _{1}}}=0,quad {frac {partial ell }{partial theta _{2}}}=0,quad ldotsquad {frac {partial ell }{partial theta _{k}}}=0~,}

conocida como las ecuaciones de probabilidad. Para algunos modelos, estas ecuaciones se pueden resolver explícitamente para ${displaystyle ,{widehat {theta ,}},,}$ pero en general no hay solución de forma cerrada al problema de la maximización es conocido o disponible, y un MLE sólo se puede encontrar a través de la optimización numérica. Otro problema es que en muestras finitas pueden existir múltiples raíces para las ecuaciones de probabilidad. Ya sea la raíz identificada ${displaystyle ,{widehat {theta ,}},}$ de las ecuaciones de probabilidad es un máximo (local) depende de si la matriz de derivados parciales y transversales de segundo orden, la llamada matriz hesiana

{displaystyle mathbf {H} left({widehat {theta ,}}right)={begin{bmatrix}left.{frac {partial ^{2}ell }{partial theta _{1}^{2}}}right|_{theta ={widehat {theta ,}}}&left.{frac {partial ^{2}ell }{partial theta _{1},partial theta _{2}}}right|_{theta ={widehat {theta ,}}}&dots &left.{frac {partial ^{2}ell }{partial theta _{1},partial theta _{k}}}right|_{theta ={widehat {theta ,}}}\left.{frac {partial ^{2}ell }{partial theta _{2},partial theta _{1}}}right|_{theta ={widehat {theta ,}}}&left.{frac {partial ^{2}ell }{partial theta _{2}^{2}}}right|_{theta ={widehat {theta ,}}}&dots &left.{frac {partial ^{2}ell }{partial theta _{2},partial theta _{k}}}right|_{theta ={widehat {theta ,}}}\vdots &vdots &ddots &vdots \left.{frac {partial ^{2}ell }{partial theta _{k},partial theta _{1}}}right|_{theta ={widehat {theta ,}}}&left.{frac {partial ^{2}ell }{partial theta _{k},partial theta _{2}}}right|_{theta ={widehat {theta ,}}}&dots &left.{frac {partial ^{2}ell }{partial theta _{k}^{2}}}right|_{theta ={widehat {theta ,}}}end{bmatrix}}~,}

es negativo semi-definido en ${displaystyle {widehat {theta ,}}}$ , como esto indica la concavidad local. Convenientemente, las distribuciones de probabilidad más comunes, en particular la familia exponencial, son concave logarítmicamente.

Espacio de parámetros restringido

Si bien el dominio de la función de probabilidad, el espacio de parámetros, es generalmente un subconjunto de dimensión finita del espacio euclidiano, a veces es necesario incorporar restricciones adicionales en el proceso de estimación. El espacio de parámetros se puede expresar como

{displaystyle Theta =left{theta:theta in mathbb {R} ^{k},;h(theta)=0right}~,}

Donde ${displaystyle ;h(theta)=left[h_{1}(theta),h_{2}(theta),ldotsh_{r}(theta)right];}$ es un mapeo de funciones de valor vectorial ${displaystyle ,mathbb {R} ^{k},}$ en ${displaystyle ;mathbb {R} ^{r}~.}$ Estimando el verdadero parámetro $theta$ pertenecientes a $Theta$ entonces, como cuestión práctica, significa encontrar el máximo de la función de probabilidad sujeto a la limitación ${displaystyle ~h(theta)=0~.}$

Teóricamente, el enfoque más natural de este problema de optimización limitada es el método de sustitución, que está "llenando" las restricciones ${displaystyle ;h_{1},h_{2},ldotsh_{r};}$ a un conjunto ${displaystyle ;h_{1},h_{2},ldotsh_{r},h_{r+1},ldotsh_{k};}$ de tal manera que ${displaystyle ;h^{ast }=left[h_{1},h_{2},ldotsh_{k}right];}$ es una función de uno a uno desde ${displaystyle mathbb {R} ^{k}}$ a sí mismo, y reparameter la función de probabilidad estableciendo ${displaystyle ;phi _{i}=h_{i}(theta _{1},theta _{2},ldotstheta _{k})~.}$ Debido a la equivariancia del estimador de probabilidad máxima, las propiedades del MLE se aplican a las estimaciones restringidas también. Por ejemplo, en una distribución normal multivariada la matriz de covariancia ${displaystyle ,Sigma ,}$ debe ser positivo-definido; esta restricción puede imponerse reemplazando ${displaystyle ;Sigma =Gamma ^{mathsf {T}}Gamma ;,}$ Donde $Gamma$ es una matriz triangular superior real y ${displaystyle Gamma ^{mathsf {T}}}$ es su transpose.

En la práctica, las restricciones suelen imponerse utilizando el método de Lagrange que, dadas las restricciones definidas anteriormente, conduce a las ecuaciones de verosimilitud restringida

{displaystyle {frac {partial ell }{partial theta }}-{frac {partial h(theta)^{mathsf {T}}}{partial theta }}lambda =0}

{displaystyle h(theta)=0;,}

Donde ${displaystyle ~lambda =left[lambda _{1},lambda _{2},ldotslambda _{r}right]^{mathsf {T}}~}$ es una columna-vector de multiplicadores de Lagrange y ${displaystyle ;{frac {partial h(theta)^{mathsf {T}}}{partial theta }};}$ es $k \times$ Matriz jacobalí de derivados parciales. Naturalmente, si las limitaciones no son vinculantes al máximo, los multiplicadores Lagrange deben ser cero. Esto a su vez permite una prueba estadística de la "validez" de la restricción, conocida como la prueba de multiplicador Lagrange.

Propiedades

Un estimador de probabilidad máxima es un estimador de extremum obtenido maximizando, como función Silencio, la función objetiva ${displaystyle {widehat {ell ,}}(theta ,;x)}$ . Si los datos son independientes e idénticos distribuidos, entonces tenemos

{displaystyle {widehat {ell ,}}(theta ,;x)={frac {1}{n}}sum _{i=1}^{n}ln f(x_{i}mid theta),}

esta es la muestra analógica de la probabilidad de registro esperada ${displaystyle ell (theta)=operatorname {mathbb {E} } [,ln f(x_{i}mid theta),]}$ , donde se toma esta expectativa con respecto a la verdadera densidad.

Los estimadores de máxima verosimilitud no tienen propiedades óptimas para muestras finitas, en el sentido de que (cuando se evalúan en muestras finitas) otros estimadores pueden tener una mayor concentración alrededor del verdadero valor del parámetro. Sin embargo, al igual que otros métodos de estimación, la estimación de máxima verosimilitud posee una serie de atractivas propiedades limitantes: a medida que el tamaño de la muestra aumenta hasta el infinito, las secuencias de estimadores de máxima verosimilitud tienen estas propiedades:

Consistencia: la secuencia de MLE converge en probabilidad al valor estimado.
Equivariancia funcional: Si ${displaystyle {hat {theta }}}$ es el estimador de probabilidad máxima para ${displaystyle theta }$ , y si ${displaystyle g(theta)}$ es cualquier transformación ${displaystyle theta }$ , entonces el estimador de probabilidad máxima para ${displaystyle alpha =g(theta)}$ es ${displaystyle {hat {alpha }}=g({hat {theta }})}$ .
Eficiencia, es decir, alcanza el límite inferior Cramér-Rao cuando el tamaño de la muestra tiende a infinito. Esto significa que ningún estimador consistente tiene un error cuadrado inferior a la MLE (o otros estimadores que alcanzan este límite), lo que también significa que MLE tiene normalidad asintotica.
Eficiencia de segundo orden después de la corrección para el sesgo.

Coherencia

En las condiciones que se describen a continuación, el estimador de probabilidad máxima es consistente. La consistencia significa que si los datos fueron generados por ${displaystyle f(cdot ,;theta _{0})}$ y tenemos un número suficientemente grande de observaciones n, entonces es posible encontrar el valor de Silencio₀ con precisión arbitraria. En términos matemáticos esto significa que n va a infinito el estimador ${displaystyle {widehat {theta ,}}}$ converge en probabilidad a su verdadero valor:

{displaystyle {widehat {theta ,}}_{mathrm {mle} } {xrightarrow {text{p}}} theta _{0}.}

Bajo condiciones ligeramente más fuertes, el estimador converge casi con seguridad (o fuertemente):

{displaystyle {widehat {theta ,}}_{mathrm {mle} } {xrightarrow {text{a.s.}}} theta _{0}.}

En aplicaciones prácticas, los datos nunca se generan por ${displaystyle f(cdot ,;theta _{0})}$ . Más bien, Failed to parse (SVG (MathML se puede activar a través del plugin del navegador): Respuesta inválida ("la extensión máxima no puede conectarse a Restbase".) de servidor "/mathoid/local/v1/": {displaystyle f(cdot,theta_0)}es un modelo, a menudo en forma idealizada, del proceso generado por los datos. Es un aforismo común en las estadísticas todos los modelos están equivocados. Así, la verdadera consistencia no ocurre en aplicaciones prácticas. Sin embargo, a menudo se considera que la consistencia es una propiedad deseable para que un estimador tenga.

Para establecer la consistencia, las siguientes condiciones son suficientes.

Identificación del modelo:
$theta neq theta _{0}quad Leftrightarrow quad f(cdot mid theta)neq f(cdot mid theta _{0}).$
En otras palabras, diferentes valores de parámetro Silencio corresponde a diferentes distribuciones dentro del modelo. Si esta condición no se mantiene, habría algún valor Silencio₁ tales que Silencio₀ y Silencio₁ generar una distribución idéntica de los datos observables. Entonces no podríamos distinguir entre estos dos parámetros incluso con una cantidad infinita de datos, estos parámetros habrían sido observadamente equivalentes.
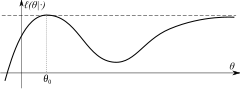
La condición de identificación es absolutamente necesaria para que el estimador ML sea consistente. Cuando esta condición sostiene, la función de probabilidad límite l()Silencio←) tiene un máximo global único Silencio₀.
Compactidad: el espacio del parámetro Θ del modelo es compacto.
La condición de identificación establece que la probabilidad de registro tiene un máximo global único. La compactidad implica que la probabilidad no puede acercarse al valor máximo arbitrariamente en algún otro punto (como se demuestra por ejemplo en la imagen de la derecha).
La compactidad es sólo una condición suficiente y no una condición necesaria. La compactidad puede sustituirse por otras condiciones, como:
- tanto la concavidad de la función de probabilidad de registro y la compactidad de algunos (no vacío) conjuntos de nivel superior de la función de probabilidad de registro, o
- existencia de un barrio compacto $N$ de $Silencio$ ₀ tal que fuera de $N$ la función de probabilidad de registro es menos que el máximo por al menos algunos $ε$ ■ 0.
Continuidad: la función $In f () x Silencio Silencio)$ es continuo $Silencio$ para casi todos los valores de $x$ :
${displaystyle operatorname {mathbb {P} } {Bigl [};ln f(xmid theta);in ;C^{0}(Theta);{Bigr ]}=1.}$
La continuidad aquí puede ser reemplazada con una condición ligeramente más débil de semi-continuidad superior.
Dominance: existe $D () x)$ integrado con respecto a la distribución $f () x Silencio Silencio 0)$ tales que
$<math alttext="{displaystyle {Bigl |}ln f(xmid theta){Bigr |}SilencioIn f()x▪ ▪ Silencio Silencio )Silencio.D()x)para todosSilencio Silencio ▪ ▪ .. .{displaystyle {Bigl TENIDO}ln f(xmid theta){Bigr ANTERITO = 0}quad {text{ for all }theta in Theta.} <img alt="{displaystyle {Bigl |}ln f(xmid theta){Bigr |}$
Por la ley uniforme de grandes números, la condición de dominio junto con la continuidad establecen la convergencia uniforme en probabilidad de la probabilidad de tronco:
${displaystyle sup _{theta in Theta }left|{widehat {ell ,}}(theta mid x)-ell (theta),right| {xrightarrow {text{p}}} 0.}$

La condición de dominio se puede emplear en el caso de observaciones i.i.d.. En el caso no i.i.d., la convergencia uniforme en probabilidad se puede comprobar mostrando que la secuencia ${displaystyle {widehat {ell ,}}(theta mid x)}$ es estocásticamente equicontínua. Si uno quiere demostrar que el estimador ML ${displaystyle {widehat {theta ,}}}$ convergencias a Silencio₀ casi seguro, entonces una condición más fuerte de convergencia uniforme casi seguramente debe ser impuesta:

{displaystyle sup _{theta in Theta }left|;{widehat {ell ,}}(theta mid x)-ell (theta);right| xrightarrow {text{a.s.}} 0.}

Además, si (como se asumió anteriormente) los datos fueron generados por ${displaystyle f(cdot ,;theta _{0})}$ , entonces en ciertas condiciones, también se puede demostrar que el estimador de probabilidad máxima converge en distribución a una distribución normal. Específicamente,

{displaystyle {sqrt {n}}left({widehat {theta ,}}_{mathrm {mle} }-theta _{0}right) xrightarrow {d} {mathcal {N}}left(0,,I^{-1}right)}

donde $I$ es la matriz de información de Fisher.

Equivarianza funcional

El estimador de probabilidad máxima selecciona el valor del parámetro que da a los datos observados la mayor probabilidad posible (o densidad de probabilidad, en el caso continuo). Si el parámetro consta de varios componentes, entonces definimos sus estimadores de máxima probabilidad separados, como el componente correspondiente del MLE del parámetro completo. Consistente con esto, si ${displaystyle {widehat {theta ,}}}$ es el MLE para $theta$ , y si $g(theta)$ es cualquier transformación $theta$ , entonces el MLE para ${displaystyle alpha =g(theta)}$ por definición

{displaystyle {widehat {alpha }}=g(,{widehat {theta ,}},).,}

Maximiza la llamada probabilidad de perfil:

{bar {L}}(alpha)=sup _{theta:alpha =g(theta)}L(theta).,

El MLE también es equivariante con respecto a ciertas transformaciones de los datos. Si $y=g(x)$ Donde $g$ es uno a uno y no depende de los parámetros a calcular, entonces las funciones de densidad satisfacen

f_{Y}(y)={frac {f_{X}(x)}{|g'(x)|}}

y por lo tanto las funciones de probabilidad $X$ y $Y$ difiere sólo por un factor que no depende de los parámetros del modelo.

Por ejemplo, los parámetros MLE de la distribución logarítmica normal son los mismos que los de la distribución normal ajustados al logaritmo de los datos.

Eficiencia

As assumed above, if the data were generated by ${displaystyle ~f(cdot ,;theta _{0})~,}$ entonces bajo ciertas condiciones, también se puede demostrar que el estimador de probabilidad máxima converge en distribución a una distribución normal. Es √n- consistente y asintomáticamente eficiente, lo que significa que alcanza el límite Cramér-Rao. Específicamente,

{displaystyle {sqrt {n,}},left({widehat {theta ,}}_{text{mle}}-theta _{0}right) xrightarrow {d} {mathcal {N}}left(0, {mathcal {I}}^{-1}right)~,}

Donde ${displaystyle ~{mathcal {I}}~}$ es la matriz de información Fisher:

{displaystyle {mathcal {I}}_{jk}=operatorname {mathbb {E} } ,{biggl [};-{frac {partial ^{2}ln f_{theta _{0}}(X_{t})}{partial theta _{j},partial theta _{k}}};{biggr ]}~.}

En particular, significa que el sesgo del estimador de máxima verosimilitud es igual a cero hasta el orden 1/√ $n$ .

Eficiencia de segundo orden después de la corrección por sesgo

Sin embargo, cuando consideramos los términos de orden superior en la expansión de la distribución de este estimador, resulta que $θ mle$ tiene un sesgo de orden 1⁄ $n$ . Este sesgo es igual a (por componentes)

{displaystyle b_{h};equiv ;operatorname {mathbb {E} } {biggl [};left({widehat {theta }}_{mathrm {mle} }-theta _{0}right)_{h};{biggr ]};=;{frac {1}{,n,}},sum _{i,j,k=1}^{m};{mathcal {I}}^{hi};{mathcal {I}}^{jk}left({frac {1}{,2,}},K_{ijk};+;J_{j,ik}right)}

Donde ${displaystyle {mathcal {I}}^{jk}}$ (con superscriptos) denota el (j,k)-t componente del inverso Matriz de información de pesca ${displaystyle {mathcal {I}}^{-1}}$ , y

{displaystyle {frac {1}{,2,}},K_{ijk};+;J_{j,ik};=;operatorname {mathbb {E} } ,{biggl [};{frac {1}{2}}{frac {partial ^{3}ln f_{theta _{0}}(X_{t})}{partial theta _{i};partial theta _{j};partial theta _{k}}}+{frac {;partial ln f_{theta _{0}}(X_{t});}{partial theta _{j}}},{frac {;partial ^{2}ln f_{theta _{0}}(X_{t});}{partial theta _{i},partial theta _{k}}};{biggr ]}~.}

Usando estas fórmulas es posible estimar el sesgo de segundo orden del estimador de máxima verosimilitud y corregir ese sesgo restándolo:

{displaystyle {widehat {theta ,}}_{text{mle}}^{*}={widehat {theta ,}}_{text{mle}}-{widehat {b,}}~.}

Este estimador es imparcial hasta los términos del pedido 1 //span> $n$ , y se denomina estimador de máxima verosimilitud corregido por sesgo.

Este estimador corregido por sesgo es eficiente de segundo orden (al menos dentro de la familia exponencial curva), lo que significa que tiene un error cuadrático medio mínimo entre todos los estimadores corregidos por sesgo de segundo orden, hasta los términos de la orden 1/ $n$ ² . Es posible continuar con este proceso, es decir, derivar el término de corrección de sesgo de tercer orden, y así sucesivamente. Sin embargo, el estimador de máxima verosimilitud no es eficiente en el tercer orden.

Relación con la inferencia bayesiana

Un estimador de máxima verosimilitud coincide con el estimador bayesiano más probable dada una distribución previa uniforme en los parámetros. De hecho, la estimación máxima a posteriori es el parámetro $θ$ que maximiza la probabilidad de $θ$ dados los datos, proporcionados por Bayes' teorema:

{displaystyle operatorname {mathbb {P} } (theta mid x_{1},x_{2},ldotsx_{n})={frac {f(x_{1},x_{2},ldotsx_{n}mid theta)operatorname {mathbb {P} } (theta)}{operatorname {mathbb {P} } (x_{1},x_{2},ldotsx_{n})}}}

Donde ${displaystyle operatorname {mathbb {P} } (theta)}$ es la distribución previa para el parámetro $Silencio$ y dónde ${displaystyle operatorname {mathbb {P} } (x_{1},x_{2},ldotsx_{n})}$ es la probabilidad de los datos promedio sobre todos los parámetros. Puesto que el denominador es independiente de $Silencio$ , el estimador bayesiano se obtiene maximizando ${displaystyle f(x_{1},x_{2},ldotsx_{n}mid theta)operatorname {mathbb {P} } (theta)}$ con respecto a $Silencio$ . Si además asumimos que el anterior ${displaystyle operatorname {mathbb {P} } (theta)}$ es una distribución uniforme, el estimador bayesiano se obtiene maximizando la función de probabilidad $f(x_{1},x_{2},ldotsx_{n}mid theta)$ . Así el estimador Bayesiano coincide con el estimador de probabilidad máxima para una distribución previa uniforme ${displaystyle operatorname {mathbb {P} } (theta)}$ .

Aplicación de la estimación de máxima verosimilitud en la teoría de decisión de Bayes

En muchas aplicaciones prácticas de aprendizaje automático, la estimación de máxima verosimilitud se utiliza como modelo para la estimación de parámetros.

La teoría de la decisión bayesiana se trata de diseñar un clasificador que minimice el riesgo esperado total, especialmente, cuando los costos (la función de pérdida) asociados con diferentes decisiones son iguales, el clasificador minimiza el error en toda la distribución.

Por lo tanto, la regla de decisión de Bayes se establece como

"decide"

{displaystyle ;w_{1};}

;operatorname {mathbb {P} } (w_{2}|x)~;~}" xmlns="http://www.w3.org/1998/Math/MathML">P⁡ ⁡ ()w1Silenciox)■P⁡ ⁡ ()w2Silenciox);{displaystyle ~operatorname {mathbb {P} (w_{1} eternax); titulado;operatorname {mathbb {} } (w_{2} perpetuax)~;~};operatorname {mathbb {P} } (w_{2}|x)~;~}" aria-hidden="true" class="mwe-math-fallback-image-inline" src="https://wikimedia.org/api/rest_v1/media/math/render/svg/efa06a173896d7791a83dffb2726b21eec60e2e0" style="vertical-align: -0.838ex; width:23.401ex; height:2.843ex;"/>

de otra manera

{displaystyle ;w_{2};}

Donde ${displaystyle ;w_{1},,w_{2};}$ son predicciones de diferentes clases. Desde una perspectiva de minimizar el error, también se puede decir como

{displaystyle w={underset {w}{operatorname {arg;max} }};int _{-infty }^{infty }operatorname {mathbb {P} } ({text{ error}}mid x)operatorname {mathbb {P} } (x),operatorname {d} x~}

dónde

{displaystyle operatorname {mathbb {P} } ({text{ error}}mid x)=operatorname {mathbb {P} } (w_{1}mid x)~}

si decidimos ${displaystyle ;w_{2};}$ y ${displaystyle ;operatorname {mathbb {P} } ({text{ error}}mid x)=operatorname {mathbb {P} } (w_{2}mid x);}$ si decidimos ${displaystyle ;w_{1};.}$

Al aplicar Bayes' teorema

{displaystyle operatorname {mathbb {P} } (w_{i}mid x)={frac {operatorname {mathbb {P} } (xmid w_{i})operatorname {mathbb {P} } (w_{i})}{operatorname {mathbb {P} } (x)}}}

y si además asumimos la función de pérdida cero o uno, que es la misma pérdida para todos los errores, la regla de decisión de Bayes se puede reformular como:

{displaystyle h_{text{Bayes}}={underset {w}{operatorname {arg;max} }},{bigl [},operatorname {mathbb {P} } (xmid w),operatorname {mathbb {P} } (w),{bigr ]};,}

Donde ${displaystyle h_{text{Bayes}}}$ es la predicción y ${displaystyle ;operatorname {mathbb {P} } (w);}$ es la probabilidad previa.

Relación con la minimización de la divergencia Kullback-Leibler y la entropía cruzada

Encontrar ${hat {theta }}$ que maximiza la probabilidad es asintoticamente equivalente a encontrar el ${hat {theta }}$ que define una distribución de probabilidad ( ${displaystyle Q_{hat {theta }}}$ ) que tiene una distancia mínima, en términos de divergencia de Kullback-Leibler, a la distribución de probabilidad real de la que se generaron nuestros datos (es decir, generados por ${displaystyle P_{theta _{0}}}$ ). En un mundo ideal, P y Q son lo mismo (y lo único desconocido es $theta$ que define P), pero incluso si no lo son y el modelo que utilizamos es mal especificado, todavía el MLE nos dará la distribución "cerca" (dentro de la restricción de un modelo Q que depende de ${hat {theta }}$ ) a la distribución real ${displaystyle P_{theta _{0}}}$ .

Proof.

For simplicity of notation, let's assume that P=Q. Let there be n i.i.d data samples $mathbf{y} = (y_1, y_2, ldots, y_n)$ from some probability ${displaystyle ysim P_{theta _{0}}}$ , that we try to estimate by finding ${hat {theta }}$ that will maximize the likelihood using $P_{{theta }}$ , then:

{displaystyle {begin{aligned}{hat {theta }}&={underset {theta }{operatorname {arg,max} }},L_{P_{theta }}(mathbf {y})={underset {theta }{operatorname {arg,max} }},P_{theta }(mathbf {y})={underset {theta }{operatorname {arg,max} }},P(mathbf {y} mid theta)\&={underset {theta }{operatorname {arg,max} }},prod _{i=1}^{n}P(y_{i}mid theta)={underset {theta }{operatorname {arg,max} }},sum _{i=1}^{n}log P(y_{i}mid theta)\&={underset {theta }{operatorname {arg,max} }},left(sum _{i=1}^{n}log P(y_{i}mid theta)-sum _{i=1}^{n}log P(y_{i}mid theta _{0})right)={underset {theta }{operatorname {arg,max} }},sum _{i=1}^{n}left(log P(y_{i}mid theta)-log P(y_{i}mid theta _{0})right)\&={underset {theta }{operatorname {arg,max} }},sum _{i=1}^{n}log {frac {P(y_{i}mid theta)}{P(y_{i}mid theta _{0})}}={underset {theta }{operatorname {arg,min} }},sum _{i=1}^{n}log {frac {P(y_{i}mid theta _{0})}{P(y_{i}mid theta)}}={underset {theta }{operatorname {arg,min} }},{frac {1}{n}}sum _{i=1}^{n}log {frac {P(y_{i}mid theta _{0})}{P(y_{i}mid theta)}}\&={underset {theta }{operatorname {arg,min} }},{frac {1}{n}}sum _{i=1}^{n}h_{theta }(y_{i})quad {underset {nto infty }{longrightarrow }}quad {underset {theta }{operatorname {arg,min} }},E[h_{theta }(y)]\&={underset {theta }{operatorname {arg,min} }},int P_{theta _{0}}(y)h_{theta }(y)dy={underset {theta }{operatorname {arg,min} }},int P_{theta _{0}}(y)log {frac {P(ymid theta _{0})}{P(ymid theta)}}dy\&={underset {theta }{operatorname {arg,min} }},D_{text{KL}}(P_{theta _{0}}parallel P_{theta })end{aligned}}}

Where ${displaystyle h_{theta }(x)=log {frac {P(xmid theta _{0})}{P(xmid theta)}}}$ . Using h helps see how we are using the law of large numbers to move from the average of h(x) to the expectancy of it using the law of the unconscious statistician. The first several transitions have to do with laws of logarithm and that finding ${hat {theta }}$ that maximizes some function will also be the one that maximizes some monotonic transformation of that function (i.e.: adding/multiplying by a constant).

Ya que la entropía cruzada es sólo la entropía de Shannon más la divergencia KL, y desde la entropía de ${displaystyle P_{theta _{0}}}$ es constante, entonces el MLE también minimiza asintoticamente la entropía cruzada.

Ejemplos

Distribución uniforme discreta

Considerar un caso n billetes de 1 a 1 n se coloca en una caja y se selecciona al azar (ver distribución uniforme); por lo tanto, el tamaño de la muestra es 1. Si n es desconocido, entonces el estimador de probabilidad máxima $widehat {n}$ de n es el número m en la entrada dibujada. (La probabilidad es 0 para n.m, 1.n para n≥m, y esto es más grande cuando n=m. Tenga en cuenta que la estimación de probabilidad máxima n ocurre en el extremo inferior de los posibles valores {m,m+ 1,...}, en lugar de en algún lugar en el "medio" de la gama de valores posibles, que resultaría en menos parcialidad.) El valor esperado del número m en el billete sorteado, y por lo tanto el valor esperado $widehat {n}$ , es (n+ 1)/2. Como resultado, con un tamaño de muestra de 1, el estimador de probabilidad máxima para n se subestimará sistemáticamente n por:n−1)/2.

Distribución discreta, espacio de parámetros finito

Supongamos que uno desea determinar qué tan sesgada es una moneda injusta. Llame a la probabilidad de sacar una "cara" p. El objetivo entonces se convierte en determinar p.

Suponga que la moneda se lanza 80 veces: es decir, la muestra podría ser algo así como x₁ = H, x₂ = T,..., x₈₀ = T, y el recuento del número de cabezas "H" es observado.

La probabilidad de sacar cruz es 1 − p (así que aquí p es θ arriba). Suponga que el resultado es 49 caras y 31 cruces, y suponga que la moneda se sacó de una caja que contiene tres monedas: una que da cara con probabilidad p = 1⁄3, uno que da cara con probabilidad p = 1⁄2 y otra que da cara con probabilidad p = 2⁄3. Las monedas han perdido sus etiquetas, por lo que se desconoce cuál era. Usando la estimación de máxima verosimilitud, se puede encontrar la moneda que tiene la mayor probabilidad, dados los datos que se observaron. Usando la función de masa de probabilidad de la distribución binomial con un tamaño de muestra igual a 80, número de éxitos igual a 49 pero para diferentes valores de p (la "probabilidad de éxito"), la La función de probabilidad (definida a continuación) toma uno de tres valores:

{displaystyle {begin{aligned}operatorname {mathbb {P} } {bigl [};mathrm {H} =49mid p={tfrac {1}{3}};{bigr ]}&={binom {80}{49}}({tfrac {1}{3}})^{49}(1-{tfrac {1}{3}})^{31}approx 0.000,\[6pt]operatorname {mathbb {P} } {bigl [};mathrm {H} =49mid p={tfrac {1}{2}};{bigr ]}&={binom {80}{49}}({tfrac {1}{2}})^{49}(1-{tfrac {1}{2}})^{31}approx 0.012,\[6pt]operatorname {mathbb {P} } {bigl [};mathrm {H} =49mid p={tfrac {2}{3}};{bigr ]}&={binom {80}{49}}({tfrac {2}{3}})^{49}(1-{tfrac {2}{3}})^{31}approx 0.054~.end{aligned}}}

La probabilidad se maximiza cuando $p$ = 2⁄3, por lo que esta es la estimación de máxima verosimilitud para $p$ .

Distribución discreta, espacio de parámetros continuo

Ahora supongamos que solo había una moneda pero su $p$ podría haber sido cualquier valor theta≤ $p$ ≤ 1. La función de probabilidad a maximizar es

{displaystyle L(p)=f_{D}(mathrm {H} =49mid p)={binom {80}{49}}p^{49}(1-p)^{31}~,}

y la maximización es sobre todos los valores posibles 0 ≤ $p$ ≤ 1.

Función de probabilidad de un valor proporcional de un proceso binomio (

n

= 10)

Una forma de maximizar esta función es diferenciar con respecto a $p$ y poner a cero:

{displaystyle {begin{aligned}0&={frac {partial }{partial p}}left({binom {80}{49}}p^{49}(1-p)^{31}right)~,\[8pt]0&=49p^{48}(1-p)^{31}-31p^{49}(1-p)^{30}\[8pt]&=p^{48}(1-p)^{30}left[49(1-p)-31pright]\[8pt]&=p^{48}(1-p)^{30}left[49-80pright]~.end{aligned}}}

Este es un producto de tres términos. El primer término es 0 cuando $p$ = 0. El segundo es 0 cuando $p$ = 1. El tercero es cero cuando $p$ = 49⁄80. La solución que maximiza la probabilidad es claramente $p$ = 49⁄80 (ya que $p$ = 0 y $p$ = 1 dan como resultado una probabilidad de 0). Por lo tanto, el estimador de máxima verosimilitud para $p$ es 49⁄80.

Este resultado se generaliza fácilmente sustituyendo una letra como $s$ en lugar de 49 para representar el número observado de & #39;éxitos' de nuestros ensayos de Bernoulli y una letra como $n$ en lugar de 80 para representar el número de ensayos de Bernoulli. Exactamente el mismo cálculo produce $s$ ⁄ $n$ cuál es la probabilidad máxima estimador para cualquier secuencia de $n$ ensayos de Bernoulli que den como resultado $s$ 'éxitos'.

Distribución continua, espacio de parámetros continuo

Para la distribución normal ${mathcal {N}}(musigma ^{2})$ que tiene función de densidad de probabilidad

{displaystyle f(xmid musigma ^{2})={frac {1}{{sqrt {2pi sigma ^{2}}} }}exp left(-{frac {(x-mu)^{2}}{2sigma ^{2}}}right),}

la función de densidad de probabilidad correspondiente para una muestra de $n$ variables aleatorias normales independientes idénticamente distribuidas (la probabilidad) es

{displaystyle f(x_{1},ldotsx_{n}mid musigma ^{2})=prod _{i=1}^{n}f(x_{i}mid musigma ^{2})=left({frac {1}{2pi sigma ^{2}}}right)^{n/2}exp left(-{frac {sum _{i=1}^{n}(x_{i}-mu)^{2}}{2sigma ^{2}}}right).}

Esta familia de distribuciones tiene dos parámetros: $Silencio = μ, σ)$ ; así que maximizamos la probabilidad, ${displaystyle {mathcal {L}}(musigma ^{2})=f(x_{1},ldotsx_{n}mid musigma ^{2})}$ , sobre ambos parámetros simultáneamente, o si es posible, individualmente.

Dado que la función logarítmica en sí misma es una función continua estrictamente creciente en el rango de la probabilidad, los valores que maximizan la probabilidad también maximizarán su logaritmo (el logaritmo de la probabilidad en sí no es necesariamente estrictamente creciente). El log-verosimilitud se puede escribir de la siguiente manera:

{displaystyle log {Bigl (}{mathcal {L}}(musigma ^{2}){Bigr)}=-{frac {,n,}{2}}log(2pi sigma ^{2})-{frac {1}{2sigma ^{2}}}sum _{i=1}^{n}(,x_{i}-mu ,)^{2}}

(Nota: el log-verosimilitud está estrechamente relacionado con la entropía de la información y la información de Fisher).

Ahora calculamos las derivadas de este log-verosimilitud de la siguiente manera.

{displaystyle {begin{aligned}0&={frac {partial }{partial mu }}log {Bigl (}{mathcal {L}}(musigma ^{2}){Bigr)}=0-{frac {;-2!n({bar {x}}-mu);}{2sigma ^{2}}}.end{aligned}}}

Donde ${bar {x}}$ es la muestra media. Esto es resuelto por

{displaystyle {widehat {mu }}={bar {x}}=sum _{i=1}^{n}{frac {,x_{i},}{n}}.}

Este es de hecho el máximo de la función, ya que es el único punto de inflexión en $μ$ y la segunda derivada es estrictamente menos que cero. Su valor esperado es igual al parámetro $μ$ de la distribución dada,

{displaystyle operatorname {mathbb {E} } {bigl [};{widehat {mu }};{bigr ]}=mu,}

que significa que el estimador de probabilidad máxima ${widehat {mu }}$ es imparcial.

Del mismo modo, diferenciamos el log-verosimilitud con respecto a $σ$ y lo igualamos a cero:

{displaystyle {begin{aligned}0&={frac {partial }{partial sigma }}log {Bigl (}{mathcal {L}}(musigma ^{2}){Bigr)}=-{frac {,n,}{sigma }}+{frac {1}{sigma ^{3}}}sum _{i=1}^{n}(,x_{i}-mu ,)^{2}.end{aligned}}}

que se resuelve con

{displaystyle {widehat {sigma }}^{2}={frac {1}{n}}sum _{i=1}^{n}(x_{i}-mu)^{2}.}

Inserción de la estimación $mu ={widehat {mu }}$ obtenemos

{displaystyle {widehat {sigma }}^{2}={frac {1}{n}}sum _{i=1}^{n}(x_{i}-{bar {x}})^{2}={frac {1}{n}}sum _{i=1}^{n}x_{i}^{2}-{frac {1}{n^{2}}}sum _{i=1}^{n}sum _{j=1}^{n}x_{i}x_{j}.}

Para calcular su valor esperado, es conveniente reescribir la expresión en términos de variables aleatorias de cero media (error estadístico) $delta _{i}equiv mu -x_{i}$ . Expresando la estimación en estas variables rendimientos

{displaystyle {widehat {sigma }}^{2}={frac {1}{n}}sum _{i=1}^{n}(mu -delta _{i})^{2}-{frac {1}{n^{2}}}sum _{i=1}^{n}sum _{j=1}^{n}(mu -delta _{i})(mu -delta _{j}).}

Simplificar la expresión anterior, utilizando los hechos que ${displaystyle operatorname {mathbb {E} } {bigl [};delta _{i};{bigr ]}=0}$ y ${displaystyle operatorname {E} {bigl [};delta _{i}^{2};{bigr ]}=sigma ^{2}}$ , nos permite obtener

{displaystyle operatorname {mathbb {E} } {bigl [};{widehat {sigma }}^{2};{bigr ]}={frac {,n-1,}{n}}sigma ^{2}.}

Esto significa que el estimador ${displaystyle {widehat {sigma }}^{2}}$ es parcial para $sigma ^{2}$ . También se puede demostrar que ${widehat {sigma }}$ es parcial para $sigma$ , pero ambos ${displaystyle {widehat {sigma }}^{2}}$ y ${widehat {sigma }}$ son consistentes.

Formally decimos que estimación máxima de probabilidad para $theta =(musigma ^{2})$ es

{displaystyle {widehat {theta ,}}=left({widehat {mu }},{widehat {sigma }}^{2}right).}

En este caso, los MLE podrían obtenerse individualmente. En general, este puede no ser el caso, y los MLE tendrían que obtenerse simultáneamente.

El logaritmo de verosimilitud normal en su máximo tiene una forma particularmente simple:

{displaystyle log {Bigl (}{mathcal {L}}({widehat {mu }},{widehat {sigma }}){Bigr)}={frac {,-n;;}{2}}{bigl (},log(2pi {widehat {sigma }}^{2})+1,{bigr)}}

Se puede demostrar que esta verosimilitud logarítmica máxima es la misma para mínimos cuadrados más generales, incluso para mínimos cuadrados no lineales. Esto se usa a menudo para determinar los intervalos de confianza aproximados basados en la probabilidad y las regiones de confianza, que generalmente son más precisos que los que usan la normalidad asintótica discutida anteriormente.

Variables no independientes

Puede ser el caso de que las variables estén correlacionadas, es decir, no independientes. Dos variables aleatorias $y_{1}$ y $y_{2}$ son independientes sólo si su función de densidad de probabilidad articular es el producto de las funciones de densidad de probabilidad individual, es decir.

{displaystyle f(y_{1},y_{2})=f(y_{1})f(y_{2}),}

Supongamos que uno construye un orden...n vector gaisiano fuera de variables aleatorias ${displaystyle (y_{1},ldotsy_{n})}$ , donde cada variable tiene medios dados por ${displaystyle (mu _{1},ldotsmu _{n})}$ . Además, permita que la matriz de covariancia sea denotada por ${displaystyle {mathit {Sigma }}}$ . La función de densidad de probabilidad conjunta de estos n variables aleatorias luego sigue una distribución normal multivariada dada por:

{displaystyle f(y_{1},ldotsy_{n})={frac {1}{(2pi)^{n/2}{sqrt {det({mathit {Sigma }})}}}}exp left(-{frac {1}{2}}left[y_{1}-mu _{1},ldotsy_{n}-mu _{n}right]{mathit {Sigma }}^{-1}left[y_{1}-mu _{1},ldotsy_{n}-mu _{n}right]^{mathrm {T} }right)}

En el caso bivariado, la función de densidad de probabilidad conjunta viene dada por:

{displaystyle f(y_{1},y_{2})={frac {1}{2pi sigma _{1}sigma _{2}{sqrt {1-rho ^{2}}}}}exp left[-{frac {1}{2(1-rho ^{2})}}left({frac {(y_{1}-mu _{1})^{2}}{sigma _{1}^{2}}}-{frac {2rho (y_{1}-mu _{1})(y_{2}-mu _{2})}{sigma _{1}sigma _{2}}}+{frac {(y_{2}-mu _{2})^{2}}{sigma _{2}^{2}}}right)right]}

En este y otros casos donde existe una función de densidad conjunta, la función de verosimilitud se define como se indicó anteriormente, en la sección "principios" utilizando esta densidad.

Ejemplo

${displaystyle X_{1}, X_{2},ldots X_{m}}$ son contados en celdas / cajas 1 hasta m; cada caja tiene una probabilidad diferente (pensar que las cajas son más grandes o más pequeñas) y fijamos el número de bolas que caen para ser $n$ : ${displaystyle x_{1}+x_{2}+cdots +x_{m}=n}$ . La probabilidad de cada caja es $p_{i}$ , con una limitación: ${displaystyle p_{1}+p_{2}+cdots +p_{m}=1}$ . Este es un caso en el que $X_{i}$ s no son independientes, la probabilidad conjunta de un vector ${displaystyle x_{1}, x_{2},ldotsx_{m}}$ se llama el multinomio y tiene la forma:

{displaystyle f(x_{1},x_{2},ldotsx_{m}mid p_{1},p_{2},ldotsp_{m})={frac {n!}{prod x_{i}!}}prod p_{i}^{x_{i}}={binom {n}{x_{1},x_{2},ldotsx_{m}}}p_{1}^{x_{1}}p_{2}^{x_{2}}cdots p_{m}^{x_{m}}}

Cada casilla tomada por separado contra todas las otras casillas es un binomio y esta es una extensión de la misma.

La log-verosimilitud de esto es:

{displaystyle ell (p_{1},p_{2},ldotsp_{m})=log n!-sum _{i=1}^{m}log x_{i}!+sum _{i=1}^{m}x_{i}log p_{i}}

Se debe tener en cuenta la restricción y utilizar los multiplicadores de Lagrange:

{displaystyle L(p_{1},p_{2},ldotsp_{m},lambda)=ell (p_{1},p_{2},ldotsp_{m})+lambda left(1-sum _{i=1}^{m}p_{i}right)}

Al plantear todas las derivadas como 0, se obtiene la estimación más natural

{displaystyle {hat {p}}_{i}={frac {x_{i}}{n}}}

Maximizar la probabilidad de registro, con y sin restricciones, puede ser un problema irresoluble en forma cerrada, entonces tenemos que usar procedimientos iterativos.

Procedimientos iterativos

Excepto en casos especiales, las ecuaciones de verosimilitud

{displaystyle {frac {partial ell (theta;mathbf {y})}{partial theta }}=0}

no se puede resolver explícitamente para un estimador ${displaystyle {widehat {theta }}={widehat {theta }}(mathbf {y})}$ . En cambio, necesitan ser resueltos iterativamente: a partir de una suposición inicial $theta$ (ensayo) ${displaystyle {widehat {theta }}_{1}}$ ), uno busca obtener una secuencia convergente ${displaystyle left{{widehat {theta }}_{r}right}}$ . Muchos métodos para este tipo de problema de optimización están disponibles, pero los más utilizados son algoritmos basados en una fórmula de actualización de la forma

{displaystyle {widehat {theta }}_{r+1}={widehat {theta }}_{r}+eta _{r}mathbf {d} _{r}left({widehat {theta }}right)}

donde el vector ${displaystyle mathbf {d} _{r}left({widehat {theta }}right)}$ indica la dirección de descenso de la r"Paso" y el escalar ${displaystyle eta _{r}}$ captura la "longitud del paso", también conocida como la tasa de aprendizaje.

Método de descenso de gradiente

(Nota: aquí se trata de un problema de maximización, por lo que se invierte el signo antes del degradado)

{displaystyle eta _{r}in mathbb {R} ^{+}}

que es lo suficientemente pequeño para la convergencia y

{displaystyle mathbf {d} _{r}left({widehat {theta }}right)=nabla ell left({widehat {theta }}_{r};mathbf {y} right)}

El método de descenso de gradiente requiere calcular el gradiente en la r-ésima iteración, pero no es necesario calcular la inversa de la derivada de segundo orden, es decir, la matriz hessiana. Por lo tanto, es computacionalmente más rápido que el método de Newton-Raphson.

Método de Newton-Raphson

{displaystyle eta _{r}=1}

{displaystyle mathbf {d} _{r}left({widehat {theta }}right)=-mathbf {H} _{r}^{-1}left({widehat {theta }}right)mathbf {s} _{r}left({widehat {theta }}right)}

Donde ${displaystyle mathbf {s} _{r}({widehat {theta }})}$ es la puntuación y ${displaystyle mathbf {H} _{r}^{-1}left({widehat {theta }}right)}$ es el inverso de la matriz hesiana de la función log-likelihood, ambos evaluaron riteración. Pero como el cálculo de la matriz hesiana es costoso computacionalmente, se han propuesto numerosas alternativas. El popular algoritmo Berndt-Hall-Hall-Hausman aproxima al Hessian con el producto exterior del gradiente esperado, tal que

{displaystyle mathbf {d} _{r}left({widehat {theta }}right)=-left[{frac {1}{n}}sum _{t=1}^{n}{frac {partial ell (theta;mathbf {y})}{partial theta }}left({frac {partial ell (theta;mathbf {y})}{partial theta }}right)^{mathsf {T}}right]^{-1}mathbf {s} _{r}left({widehat {theta }}right)}

Métodos cuasi-newton

Otros métodos cuasi-Newton utilizan actualizaciones secantes más elaboradas para dar una aproximación de la matriz de Hessian.

Davidon - Fletcher - Fórmula de Powell

La fórmula

DFP encuentra una solución simétrica, positiva y más cercana al valor aproximado actual de la derivada de segundo orden:

{displaystyle mathbf {H} _{k+1}=left(I-gamma _{k}y_{k}s_{k}^{mathsf {T}}right)mathbf {H} _{k}left(I-gamma _{k}s_{k}y_{k}^{mathsf {T}}right)+gamma _{k}y_{k}y_{k}^{mathsf {T}},}

dónde

{displaystyle y_{k}=nabla ell (x_{k}+s_{k})-nabla ell (x_{k}),}

{displaystyle gamma _{k}={frac {1}{y_{k}^{T}s_{k}}},}

{displaystyle s_{k}=x_{k+1}-x_{k}.}

Algoritmo de Broyden-Fletcher-Goldfarb-Shanno

BFGS también da una solución que es simétrica y definida positiva:

{displaystyle B_{k+1}=B_{k}+{frac {y_{k}y_{k}^{mathsf {T}}}{y_{k}^{mathsf {T}}s_{k}}}-{frac {B_{k}s_{k}s_{k}^{mathsf {T}}B_{k}^{mathsf {T}}}{s_{k}^{mathsf {T}}B_{k}s_{k}}}}

dónde

{displaystyle y_{k}=nabla ell (x_{k}+s_{k})-nabla ell (x_{k}),}

{displaystyle s_{k}=x_{k+1}-x_{k}.}

El método

BFGS no está garantizado que converge a menos que la función tenga una expansión cuadrática de Taylor cerca de un óptimo. Sin embargo, los BFG pueden tener un rendimiento aceptable incluso para instancias de optimización no suaves

Fisher ' s anotando

Otro método popular es reemplazar al Hessian con la matriz de información Fisher, ${displaystyle {mathcal {I}}(theta)=operatorname {mathbb {E} } left[mathbf {H} _{r}left({widehat {theta }}right)right]}$ , dándonos el algoritmo de puntuación de Fisher. Este procedimiento es estándar en la estimación de muchos métodos, como modelos lineales generalizados.

Aunque son populares, los métodos cuasi-Newton pueden converger en un punto estacionario que no es necesariamente un máximo local o global, sino un mínimo local o un punto de silla. Por lo tanto, es importante evaluar la validez de la solución obtenida de las ecuaciones de verosimilitud, verificando que la hessiana, evaluada en la solución, sea definida negativa y bien condicionada.

Historia

Ronald Fisher en 1913

Los primeros usuarios de máxima verosimilitud fueron Carl Friedrich Gauss, Pierre-Simon Laplace, Thorvald N. Thiele y Francis Ysidro Edgeworth. Sin embargo, su uso generalizado aumentó entre 1912 y 1922 cuando Ronald Fisher recomendó, popularizó ampliamente y analizó cuidadosamente la estimación de máxima verosimilitud (con intentos infructuosos de demostración).

La estimación de máxima verosimilitud finalmente trascendió la justificación heurística en una prueba publicada por Samuel S. Wilks en 1938, ahora llamada Wilks' teorema. El teorema muestra que el error en el logaritmo de los valores de probabilidad para las estimaciones de múltiples observaciones independientes tiene una distribución asintótica de χ 2, lo que permite la determinación conveniente de una región de confianza alrededor de cualquier estimación de los parámetros. La única parte difícil de la prueba de Wilks depende del valor esperado de la matriz de información de Fisher, que es proporcionada por un teorema probado por Fisher. Wilks continuó mejorando la generalidad del teorema a lo largo de su vida, y su demostración más general se publicó en 1962.

Varios autores han proporcionado revisiones del desarrollo de la estimación de máxima verosimilitud.

Contenido relacionado

Más resultados...