Estequiometría

format_list_bulleted Contenido keyboard_arrow_down

ImprimirCitar

Cálculo de cantidades relativas de reactantes y productos en reacciones químicas

Un diagrama estoquiométrico de la reacción de combustión del metano.

Estequiometría se refiere a la relación entre las cantidades de reactivos y productos antes, durante y después de las reacciones químicas.

La estequiometría se basa en la ley de conservación de la masa, en la que la masa total de los reactivos es igual a la masa total de los productos, lo que permite comprender que las relaciones entre las cantidades de reactivos y productos suelen formar una proporción de números enteros positivos. Esto significa que si se conocen las cantidades de los reactivos separados, entonces se puede calcular la cantidad del producto. Por el contrario, si un reactivo tiene una cantidad conocida y la cantidad de los productos se puede determinar empíricamente, entonces también se puede calcular la cantidad de los otros reactivos.

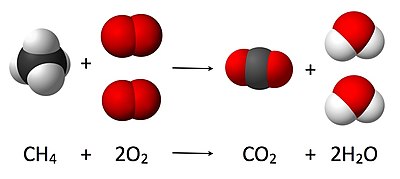
Esto se ilustra en la imagen aquí, donde la ecuación balanceada es:

CH₄ + 2 O₂ → CO₂ + 2 H₂O

Aquí, una molécula de metano reacciona con dos moléculas de oxígeno gaseoso para producir una molécula de dióxido de carbono y dos moléculas de agua. Esta ecuación química particular es un ejemplo de combustión completa. La estequiometría mide estas relaciones cuantitativas y se utiliza para determinar la cantidad de productos y reactivos que se producen o se necesitan en una reacción dada. La descripción de las relaciones cuantitativas entre sustancias que participan en reacciones químicas se conoce como reacción estequiométrica. En el ejemplo anterior, la estequiometría de reacción mide la relación entre las cantidades de metano y oxígeno que reaccionan para formar dióxido de carbono y agua.

Debido a la conocida relación entre los moles y los pesos atómicos, las proporciones a las que se llega mediante la estequiometría se pueden usar para determinar cantidades por peso en una reacción descrita por una ecuación balanceada. Esto se llama estequiometría de composición.

La estequiometría de gases se ocupa de las reacciones que involucran gases, donde los gases están a una temperatura, presión y volumen conocidos y se puede suponer que son gases ideales. Para los gases, la relación de volumen es idealmente la misma según la ley de los gases ideales, pero la relación de masa de una sola reacción debe calcularse a partir de las masas moleculares de los reactivos y productos. En la práctica, debido a la existencia de isótopos, se utilizan las masas molares para calcular la relación de masas.

Etimología

El término estequiometría fue utilizado por primera vez por Jeremias Benjamin Richter en 1792 cuando se publicó el primer volumen de Estequiometría o el arte de medir los elementos químicos de Richter.. El término se deriva de las palabras griegas antiguas στοιχεῖον stoicheion "elemento& #34; y μέτρον metron "medida". En griego patrístico, Nicéforo usó la palabra Stoichiometria para referirse al número de líneas del Nuevo Testamento canónico y algunos de los apócrifos.

Definición

Una cantidad estequiométrica o relación estequiométrica de un reactivo es la cantidad o proporción óptima en la que, suponiendo que la reacción continúa hasta completarse:

Todo el reactivo se consume
No hay deficiencia del reagente
No hay exceso de reactivo.

La estequiometría se basa en leyes muy básicas que ayudan a comprenderla mejor, es decir, la ley de conservación de la masa, la ley de las proporciones definidas (es decir, la ley de la composición constante), la ley de las proporciones múltiples y la ley de la recíproca dimensiones. En general, las reacciones químicas se combinan en proporciones definidas de sustancias químicas. Dado que las reacciones químicas no pueden crear ni destruir materia, ni transmutar un elemento en otro, la cantidad de cada elemento debe ser la misma durante toda la reacción. Por ejemplo, el número de átomos de un elemento X dado en el lado del reactivo debe ser igual al número de átomos de ese elemento en el lado del producto, ya sea que todos esos átomos estén o no involucrados en una reacción.

Las reacciones químicas, como operaciones unitarias macroscópicas, consisten simplemente en un gran número de reacciones elementales, donde una sola molécula reacciona con otra molécula. Como las moléculas que reaccionan (o fracciones) consisten en un conjunto definido de átomos en una proporción de enteros, la proporción entre los reactivos en una reacción completa también está en una proporción de enteros. Una reacción puede consumir más de una molécula, y el número estequiométrico cuenta este número, definido como positivo para productos (agregados) y negativo para reactivos (eliminados). Los coeficientes sin signo generalmente se denominan coeficientes estequiométricos.

Cada elemento tiene una masa atómica y, considerando las moléculas como colecciones de átomos, los compuestos tienen una masa molar definida. Por definición, la masa molar del carbono-12 es 12 g/mol. El número de moléculas por mol en una sustancia viene dado por la constante de Avogadro. Así, para calcular la estequiometría por masa, el número de moléculas necesarias para cada reactivo se expresa en moles y se multiplica por la masa molar de cada uno para dar la masa de cada reactivo por mol de reacción. Las proporciones de masa se pueden calcular dividiendo cada una por el total de la reacción completa.

Los elementos en su estado natural son mezclas de isótopos de diferente masa; por lo tanto, las masas atómicas y, por lo tanto, las masas molares no son exactamente números enteros. Por ejemplo, en lugar de una proporción exacta de 14:3, 17,04 kg de amoníaco consisten en 14,01 kg de nitrógeno y 3 × 1,01 kg de hidrógeno, porque el nitrógeno natural incluye una pequeña cantidad de nitrógeno-15, y el hidrógeno natural incluye hidrógeno-2 (deuterio).

Un reactivo estequiométrico es un reactivo que se consume en una reacción, a diferencia de un reactivo catalítico, que no se consume en la reacción general porque reacciona en un paso y se regenera en otro paso.

Conversión de gramos a moles

La estequiometría no solo se usa para equilibrar ecuaciones químicas, sino que también se usa en conversiones, es decir, convertir de gramos a moles usando la masa molar como factor de conversión, o de gramos a mililitros usando la densidad. Por ejemplo, para encontrar la cantidad de NaCl (cloruro de sodio) en 2,00 g, se haría lo siguiente:

{displaystyle {frac {2.00{mbox{ g NaCl}}}{58.44{mbox{ g NaCl mol}}^{-1}}}=0.0342 {text{mol}}}

En el ejemplo anterior, cuando se escriben en forma de fracción, las unidades de gramos forman una identidad multiplicativa, que es equivalente a uno (g/g = 1), con la cantidad resultante en moles (la unidad que se necesitaba), como se muestra en la siguiente ecuación,

{displaystyle left({frac {2.00{mbox{ g NaCl}}}{1}}right)left({frac {1{mbox{ mol NaCl}}}{58.44{mbox{ g NaCl}}}}right)=0.0342 {text{mol}}}

Proporción molar

La estequiometría se usa a menudo para equilibrar ecuaciones químicas (reacción estequiométrica). Por ejemplo, los dos gases diatómicos, hidrógeno y oxígeno, pueden combinarse para formar un líquido, agua, en una reacción exotérmica, como se describe en la siguiente ecuación:

2H
₂ + O
₂ → 2H
₂O

La estequiometría de reacción describe la proporción 2:1:2 de moléculas de hidrógeno, oxígeno y agua en la ecuación anterior.

La relación molar permite la conversión entre moles de una sustancia y moles de otra. Por ejemplo, en la reacción

2CH
₃Oh. + 3O
₂ → 2CO
₂ + 4H
₂O

la cantidad de agua que se producirá por la combustión de 0,27 moles de CH
₃OH se obtiene utilizando el molar relación entre CH
₃OH y H
₂ O de 2 a 4.

left({frac {0.27{mbox{ mol }}mathrm {CH_{3}OH} }{1}}right)left({frac {4{mbox{ mol }}mathrm {H_{2}O} }{2{mbox{ mol }}mathrm {CH_{3}OH} }}right)=0.54 {text{mol }}mathrm {H_{2}O}

El término estequiometría también se usa a menudo para las proporciones molares de elementos en compuestos estequiométricos (estequiometría de composición). Por ejemplo, la estequiometría del hidrógeno y el oxígeno en H₂O es 2:1. En los compuestos estequiométricos, las proporciones molares son números enteros.

Determinación de la cantidad de producto

La estequiometría también se puede usar para encontrar la cantidad de un producto producido por una reacción. Si se agregara un trozo de cobre sólido (Cu) a una solución acuosa de nitrato de plata (AgNO₃), la plata (Ag) sería reemplazada en una sola reacción de desplazamiento formando nitrato de cobre (II) acuoso. (Cu(NO₃)₂) y plata maciza. ¿Cuánta plata se produce si se agregan 16,00 gramos de Cu a la solución de exceso de nitrato de plata?

Se utilizarían los siguientes pasos:

Escribe y equilibra la ecuación
Masa a topos: Convertir gramos de Cu en moles de Cu
Mole ratio: Convertir moles de Cu en moles de Ag producidos
Molo en masa: Convertir moles de Ag en gramos de Ag producidos

La ecuación balanceada completa sería:

Cu + 2AgNO
₃ → Cu(NO
₃)
₂ + 2Ag

Para el paso de masa a mol, la masa de cobre (16,00 g) se convertiría en moles de cobre dividiendo la masa de cobre por su masa molecular: 63,55 g/mol.

left({frac {16.00{mbox{ g Cu}}}{1}}right)left({frac {1{mbox{ mol Cu}}}{63.55{mbox{ g Cu}}}}right)=0.2518 {text{mol Cu}}

Ahora que se encontró la cantidad de Cu en moles (0,2518), podemos establecer la relación molar. Esto se encuentra mirando los coeficientes en la ecuación balanceada: Cu y Ag están en una proporción de 1:2.

left({frac {0.2518{mbox{ mol Cu}}}{1}}right)left({frac {2{mbox{ mol Ag}}}{1{mbox{ mol Cu}}}}right)=0.5036 {text{mol Ag}}

Ahora que se sabe que los moles de Ag producidos son 0,5036 mol, convertimos esta cantidad en gramos de Ag producidos para llegar a la respuesta final:

left({frac {0.5036{mbox{ mol Ag}}}{1}}right)left({frac {107.87{mbox{ g Ag}}}{1{mbox{ mol Ag}}}}right)=54.32 {text{g Ag}}

Este conjunto de cálculos se puede condensar aún más en un solo paso:

m_{mathrm {Ag} }=left({frac {16.00{mbox{ g }}mathrm {Cu} }{1}}right)left({frac {1{mbox{ mol }}mathrm {Cu} }{63.55{mbox{ g }}mathrm {Cu} }}right)left({frac {2{mbox{ mol }}mathrm {Ag} }{1{mbox{ mol }}mathrm {Cu} }}right)left({frac {107.87{mbox{ g }}mathrm {Ag} }{1{mbox{ mol Ag}}}}right)=54.32{mbox{ g}}

Más ejemplos

Para el propano (C₃H₈) que reacciona con el oxígeno gaseoso (O₂), la ecuación química balanceada es:

C₃H₈ + 5 O₂ → 3 CO₂ + 4 H₂O

La masa de agua que se forma si se queman 120 g de propano (C₃H₈) en exceso de oxígeno es entonces

m_{mathrm {H_{2}O} }=left({frac {120.{mbox{ g }}mathrm {C_{3}H_{8}} }{1}}right)left({frac {1{mbox{ mol }}mathrm {C_{3}H_{8}} }{44.09{mbox{ g }}mathrm {C_{3}H_{8}} }}right)left({frac {4{mbox{ mol }}mathrm {H_{2}O} }{1{mbox{ mol }}mathrm {C_{3}H_{8}} }}right)left({frac {18.02{mbox{ g }}mathrm {H_{2}O} }{1{mbox{ mol }}mathrm {H_{2}O} }}right)=196{mbox{ g}}

Relación estequiométrica

La estequiometría también se usa para encontrar la cantidad correcta de un reactivo para "completamente" reaccionar con el otro reactivo en una reacción química, es decir, las cantidades estequiométricas que darían como resultado que no sobraran reactivos cuando se lleve a cabo la reacción. A continuación se muestra un ejemplo usando la reacción de la termita,

Fe₂O₃ + 2 Al → Al₂O₃ + 2 Fe

Esta ecuación muestra que 1 mol de óxido de hierro (III) y 2 moles de aluminio producirán 1 mol de óxido de aluminio y 2 moles de hierro. Entonces, para reaccionar completamente con 85,0 g de óxido de hierro (III) (0,532 mol), se necesitan 28,7 g (1,06 mol) de aluminio.

m_{mathrm {Al} }=left({frac {85.0{mbox{ g }}mathrm {Fe_{2}O_{3}} }{1}}right)left({frac {1{mbox{ mol }}mathrm {Fe_{2}O_{3}} }{159.7{mbox{ g }}mathrm {Fe_{2}O_{3}} }}right)left({frac {2{mbox{ mol Al}}}{1{mbox{ mol }}mathrm {Fe_{2}O_{3}} }}right)left({frac {26.98{mbox{ g Al}}}{1{mbox{ mol Al}}}}right)=28.7{mbox{ g}}

Reactivo limitante y rendimiento porcentual

El reactivo limitante es el reactivo que limita la cantidad de producto que se puede formar y se consume por completo cuando se completa la reacción. Un reactivo en exceso es un reactivo que queda una vez que la reacción se ha detenido debido a que el reactivo limitante se agotó.

Considere la ecuación de tostar sulfuro de plomo (II) (PbS) en oxígeno (O₂) para producir óxido de plomo (II) (PbO) y dióxido de azufre (SO₂):

2PbS + 3O
₂ → 2PbO + 2SO
₂

Para determinar el rendimiento teórico de óxido de plomo(II) si se calientan 200,0 g de sulfuro de plomo(II) y 200,0 g de oxígeno en un recipiente abierto:

m_{mathrm {PbO} }=left({frac {200.0{mbox{ g }}mathrm {PbS} }{1}}right)left({frac {1{mbox{ mol }}mathrm {PbS} }{239.27{mbox{ g }}mathrm {PbS} }}right)left({frac {2{mbox{ mol }}mathrm {PbO} }{2{mbox{ mol }}mathrm {PbS} }}right)left({frac {223.2{mbox{ g }}mathrm {PbO} }{1{mbox{ mol }}mathrm {PbO} }}right)=186.6{mbox{ g}}

m_{mathrm {PbO} }=left({frac {200.0{mbox{ g }}mathrm {O_{2}} }{1}}right)left({frac {1{mbox{ mol }}mathrm {O_{2}} }{32.00{mbox{ g }}mathrm {O_{2}} }}right)left({frac {2{mbox{ mol }}mathrm {PbO} }{3{mbox{ mol }}mathrm {O_{2}} }}right)left({frac {223.2{mbox{ g }}mathrm {PbO} }{1{mbox{ mol }}mathrm {PbO} }}right)=930.0{mbox{ g}}

Debido a que se produce una menor cantidad de PbO para los 200,0 g de PbS, está claro que el PbS es el reactivo limitante.

En realidad, el rendimiento real no es el mismo que el rendimiento teórico calculado estequiométricamente. El rendimiento porcentual, entonces, se expresa en la siguiente ecuación:

{displaystyle {mbox{percent yield}}={frac {mbox{actual yield}}{mbox{theoretical yield}}}}

Si se obtienen 170,0 g de óxido de plomo (II), el porcentaje de rendimiento se calcularía de la siguiente manera:

{displaystyle {mbox{percent yield}}={frac {mbox{170.0 g PbO}}{mbox{186.6 g PbO}}}=91.12%}

Ejemplo

Considere la siguiente reacción, en la que el cloruro de hierro (III) reacciona con sulfuro de hidrógeno para producir sulfuro de hierro (III) y cloruro de hidrógeno:

2 FeCl₃ + 3 H₂S → Fe₂S₃ + 6 HCl

Las masas estequiométricas para esta reacción son:

324.41 g FeCl₃, 102.25 g H₂S, 207.89 g Fe₂S₃, 218.77 g HCl

Suponga que 90,0 g de FeCl₃ reaccionan con 52,0 g de H₂S. Para encontrar el reactivo limitante y la masa de HCl producido por la reacción, cambiamos las cantidades anteriores por un factor de 90/324,41 y obtenemos las siguientes cantidades:

90.00 g FeCl₃, 28.37 g H₂S, 57.67 g Fe₂S₃, 60,69 g HCl

El reactivo limitante (o reactivo) es FeCl₃, ya que se consumen los 90,00 g mientras que solo se consumen 28,37 g de H₂S. Por lo tanto, quedan 52,0 − 28,4 = 23,6 g H₂S en exceso. La masa de HCl producido es de 60,7 g.

Nota: al observar la estequiometría de la reacción, uno podría haber adivinado que FeCl₃ es el reactivo limitante; Se utiliza tres veces más FeCl₃ en comparación con H₂S (324 g frente a 102 g).

Diferentes estequiometrías en reacciones competitivas

A menudo, es posible más de una reacción con los mismos materiales de partida. Las reacciones pueden diferir en su estequiometría. Por ejemplo, la metilación del benceno (C₆H₆), a través de una reacción de Friedel-Crafts usando AlCl3 como catalizador, puede producir (C₆₎H₅CH₃), doblemente metilado (C₆H₄(CH₃)₂), o aún más altamente metilado (C₆H_6−n(CH₃)_n), como se muestra en el siguiente ejemplo,

C₆H₆ + CH₃Cl → C₆H₅CH₃ + HCl

C₆H₆ + 2 CH₃Cl → C₆H₄(CH)₃)₂ + 2 HCl

C₆H₆ + nCH₃Cl → C₆H_{6 an}(CH)₃)_n + nHCl

En este ejemplo, la reacción que tiene lugar está controlada en parte por las concentraciones relativas de los reactivos.

Coeficiente estequiométrico y número estequiométrico

En términos sencillos, el coeficiente estequiométrico de cualquier componente dado es el número de moléculas y/o unidades de fórmula que participan en la reacción tal como está escrita. Un concepto relacionado es el número estequiométrico (usando la nomenclatura IUPAC), donde el coeficiente estequiométrico se multiplica por +1 para todos los productos y por −1 para todos los reactivos.

Por ejemplo, en la reacción CH₄ + 2 O₂ → CO2 + 2 H₂ O, el número estequiométrico de CH₄ es −1, el número estequiométrico de O₂ es −2, para CO₂ sería +1 y para H₂O es +2.

En términos más técnicamente precisos, el número estequiométrico en un sistema de reacción química del componente iésimo se define como

nu _{i}={frac {Delta N_{i}}{Delta xi }},

{displaystyle Delta N_{i}=nu _{i},Delta xi ,}

Donde $N_{i}$ es el número de moléculas de i, y $xi$ es la variable de progreso o el alcance de la reacción.

El número estequiométrico $nu _{i}$ representa el grado en que una especie química participa en una reacción. La convención es asignar números negativos a reaccionarios (que se consumen) y positivos a productos, consistente con la convención que aumentar el grado de reacción corresponderá a cambiar la composición de los reaccionarios hacia los productos. Sin embargo, cualquier reacción puede ser vista como ir en la dirección inversa, y en ese punto de vista, cambiaría en la dirección negativa para bajar la energía libre del sistema Gibbs. Ya sea una reacción en realidad voluntad ir en la dirección hacia adelante seleccionada arbitrariamente o no depende de las cantidades de las sustancias presentes en cualquier momento dado, que determina la kinetica y la termodinámica, es decir, si el equilibrio está en el derecho o el izquierda del estado inicial,

En los mecanismos de reacción, los coeficientes estequiométricos para cada paso son siempre números enteros, ya que las reacciones elementales siempre involucran moléculas enteras. Si se usa una representación compuesta de una reacción general, algunas pueden ser fracciones racionales. A menudo hay especies químicas presentes que no participan en una reacción; sus coeficientes estequiométricos son por lo tanto cero. Cualquier especie química que se regenere, como un catalizador, también tiene un coeficiente estequiométrico de cero.

El caso más simple posible es una isomerización

A → B

en el que $ν B = 1$ ya que se produce una molécula de B cada vez que ocurre la reacción, mientras que $ν A = -1$ ya que una molécula de A se consume necesariamente. En cualquier reacción química, no sólo se conserva la masa total, sino también el número de átomos de cada tipo, y esto impone las restricciones correspondientes sobre los posibles valores de los coeficientes estequiométricos.

Por lo general, hay múltiples reacciones que ocurren simultáneamente en cualquier sistema de reacción natural, incluidas las de la biología. Dado que cualquier componente químico puede participar en varias reacciones simultáneamente, el número estequiométrico del iésimo componente en la késima reacción se define como

nu _{ik}={frac {partial N_{i}}{partial xi _{k}}},

de manera que el cambio total (diferencial) en la cantidad del iésimo componente es

{displaystyle dN_{i}=sum _{k}nu _{ik},dxi _{k}.,}

Los grados de reacción proporcionan la forma más clara y explícita de representar el cambio de composición, aunque todavía no se usan mucho.

Con sistemas de reacción complejos, suele ser útil considerar la representación de un sistema de reacción en términos de las cantidades de sustancias químicas presentes ${N i}$ (variables de estado) y la representación en términos de los grados de libertad de composición reales, expresados por los grados de reacción ${ξ k}$ . La transformación de un vector que expresa las extensiones a un vector que expresa las cantidades utiliza una matriz rectangular cuyos elementos son los números estequiométricos $[ν i k]$ .

El máximo y el mínimo para cualquier ξ_k ocurren cada vez que se agota el primero de los reactivos para la reacción directa; o el primero de los "productos" se agota si se considera que la reacción es empujada en la dirección inversa. Esta es una restricción puramente cinemática en la reacción símplex, un hiperplano en el espacio de composición, o espacio N, cuya dimensionalidad es igual al número de reacciones químicas linealmente independientes. Esto es necesariamente menor que el número de componentes químicos, ya que cada reacción manifiesta una relación entre al menos dos químicos. La región accesible del hiperplano depende de las cantidades de cada especie química realmente presentes, un hecho contingente. Diferentes cantidades de este tipo pueden incluso generar diferentes hiperplanos, todos compartiendo la misma estequiometría algebraica.

De acuerdo con los principios de la cinética química y el equilibrio termodinámico, toda reacción química es reversible, al menos hasta cierto punto, por lo que cada punto de equilibrio debe ser un punto interior del símplex. Como consecuencia, no se producirán extremos para los ξ a menos que se prepare un sistema experimental con cantidades iniciales cero de algunos productos.

El número de reacciones físicamente independientes puede ser incluso mayor que el número de componentes químicos y depende de los distintos mecanismos de reacción. Por ejemplo, puede haber dos (o más) caminos de reacción para la isomería anterior. La reacción puede ocurrir sola, pero más rápido y con diferentes intermediarios, en presencia de un catalizador.

Las "unidades" (adimensionales) pueden tomarse como moléculas o moles. Los moles son los más utilizados, pero es más sugerente representar las reacciones químicas incrementales en términos de moléculas. Los Ns y ξs se reducen a unidades molares al dividirlos por la constante de Avogadro. Si bien se pueden usar unidades de masa dimensional, los comentarios sobre números enteros ya no son aplicables.

Matriz de estequiometría

En reacciones complejas, las estequiometrías a menudo se representan en una forma más compacta llamada matriz de estequiometría. La matriz estequiométrica se denota con el símbolo N.

Si una red de reacción tiene n reacciones y m especies moleculares participantes, entonces la matriz de estequiometría tendrá correspondientemente m filas y n columnas.

Por ejemplo, considere el sistema de reacciones que se muestra a continuación:

S₁ → S₂

5 S₃ + S₂ → 4 S₃ + 2 S₂

S₃ → S₄

S₄ → S₅

Este sistema comprende cuatro reacciones y cinco especies moleculares diferentes. La matriz estequiométrica para este sistema se puede escribir como:

mathbf {N} ={begin{bmatrix}-1&0&0&0\1&1&0&0\0&-1&-1&0\0&0&1&-1\0&0&0&1\end{bmatrix}}

donde las filas corresponden a S₁, S₂, S₃, S₄ y S₅, respectivamente. Tenga en cuenta que el proceso de convertir un esquema de reacción en una matriz de estequiometría puede ser una transformación con pérdidas: por ejemplo, las estequiometrías en la segunda reacción se simplifican cuando se incluyen en la matriz. Esto significa que no siempre es posible recuperar el esquema de reacción original a partir de una matriz estequiométrica.

A menudo, la matriz estequiométrica se combina con el vector de tasas, v, y el vector de especies, x para formar una ecuación compacta que describe las tasas de cambio de las especies moleculares.:

{displaystyle {frac {dmathbf {x} }{dt}}=mathbf {N} cdot mathbf {v}.}

Estequiometría de gases

Estequiometría de gases es la relación cuantitativa (ratio) entre reactivos y productos en una reacción química con reacciones que producen gases. La estequiometría de gases se aplica cuando se supone que los gases producidos son ideales y se conocen la temperatura, la presión y el volumen de los gases. Para estos cálculos se utiliza la ley de los gases ideales. A menudo, pero no siempre, la temperatura y la presión estándar (STP) se toman como 0 °C y 1 bar y se utilizan como condiciones para los cálculos estequiométricos de gases.

Los cálculos de estequiometría de gases resuelven el volumen o la masa desconocidos de un producto o reactivo gaseoso. Por ejemplo, si quisiéramos calcular el volumen de NO₂ gaseoso que se produce a partir de la combustión de 100 g de NH₃, mediante la reacción:

4 NH₃ g) + 7 O₂ g) → 4 NO₂ g) + 6 H₂O (l)

realizaríamos los siguientes cálculos:

100,mathrm {g,NH_{3}} cdot {frac {1,mathrm {mol,NH_{3}} }{17.034,mathrm {g,NH_{3}} }}=5.871,mathrm {mol,NH_{3}}

Hay una relación molar de 1:1 de NH₃ a NO₂ en la reacción de combustión equilibrada anterior, por lo que 5,871 mol de NO₂ se formará. Emplearemos la ley de los gases ideales para resolver el volumen a 0 °C (273,15 K) y 1 atmósfera utilizando la constante de la ley de los gases de R = 0,08206 L·atm·K⁻¹·mol⁻¹:

{begin{aligned}PV&=nRT\V&={frac {nRT}{P}}\&={frac {5.871cdot 0.08206cdot 273.15}{1}}\&=131.597,mathrm {L,NO_{2}} end{aligned}}

La estequiometría de gases a menudo implica tener que conocer la masa molar de un gas, dada la densidad de ese gas. La ley de los gases ideales se puede reorganizar para obtener una relación entre la densidad y la masa molar de un gas ideal:

rho ={frac {m}{V}}

n={frac {m}{M}}

y así:

rho ={frac {MP}{R,T}}

donde:

P= presión absoluta de gas
V= volumen de gas
n= cantidad (medida en topos)
R= constante de la ley del gas ideal universal
T= temperatura absoluta de gas
***= densidad de gas en T y P
m= masa de gas
M= masa molar de gas

Relaciones aire-combustible estequiométricas de combustibles comunes

En la reacción de combustión, el oxígeno reacciona con el combustible, y el punto donde se consume exactamente todo el oxígeno y se quema todo el combustible se define como el punto estequiométrico. Con más oxígeno (combustión sobreestequiométrica), parte de él permanece sin reaccionar. Asimismo, si la combustión es incompleta por falta de suficiente oxígeno, el combustible queda sin reaccionar. (El combustible sin reaccionar también puede permanecer debido a una combustión lenta o una mezcla insuficiente de combustible y oxígeno; esto no se debe a la estequiometría). Los diferentes combustibles de hidrocarburos tienen diferentes contenidos de carbono, hidrógeno y otros elementos, por lo que su estequiometría varía.

Tenga en cuenta que el oxígeno constituye solo el 20,95 % del volumen del aire y solo el 23,20 % de su masa. Las relaciones aire-combustible enumeradas a continuación son mucho más altas que las relaciones equivalentes de oxígeno-combustible, debido a la alta proporción de gases inertes en el aire.

Combustible	Relación por masa	Relación por volumen	Gasto porcentual por masa	Reacción principal
Gasolina	14.7: 1	—	6,8%	2C ₈H ₁₈ + 25O ₂ → 16CO ₂ + 18H ₂O
Gas natural	17.2: 1	9.7: 1	5,8%	CH ₄ + 2O ₂ → CO ₂ + 2H ₂O
Propane (LP)	15.67: 1	23.9: 1	6.45%	C ₃H ₈ + 5O ₂ → 3CO ₂ + 4H ₂O
Ethanol	9: 1	—	11,1%	C ₂H ₆O + 3O ₂ → 2CO ₂ + 3H ₂O
Metanol	6.47: 1	—	15,6%	2CH ₄O + 3O ₂ → 2CO ₂ + 4H ₂O
n-Butanol	11.2: 1	—	8.2%	C ₄H ₁₀O + 6O ₂ → 4CO ₂ + 5H ₂O
Hidrogen	34.3: 1	2.39: 1	2,9%	2H ₂ + O ₂ → 2H ₂O
Diesel	14.5: 1	—	6,8%	2C ₁₂H ₂₆ + 37O ₂ → 24CO ₂ + 26H ₂O
Metano	17.19: 1	9.52: 1	5.5%	CH ₄ + 2O ₂ → CO ₂ + 2H ₂O
Acetileno	13.26: 1	11.92: 1	7.0%	2C ₂H ₂ + 5O ₂ → 4CO ₂ + 2H ₂O
Ethane	16.07: 1	16.68: 1	5,9%	2C ₂H ₆ + 7O ₂ → 4CO ₂ + 6H ₂O
Butane	15.44: 1	30.98: 1	6,1%	2C ₄H ₁₀ + 13O ₂ → 8CO ₂ + 10H ₂O
Pentane	15.31: 1	38.13: 1	6,1%	C ₅H ₁₂ + 8O ₂ → 5CO ₂ + 6H ₂O

Los motores de gasolina pueden funcionar con una relación aire-combustible estequiométrica, porque la gasolina es bastante volátil y se mezcla (rocía o carbura) con el aire antes del encendido. Los motores diésel, por el contrario, funcionan de forma pobre, con más aire disponible del que requeriría la simple estequiometría. El combustible diesel es menos volátil y se quema de manera efectiva a medida que se inyecta.

Contenido relacionado

Más resultados...