Estática (mecánica)
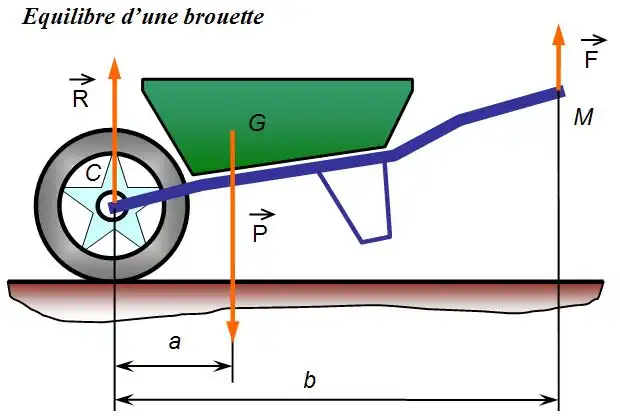
La estática es la rama de la mecánica que se ocupa del análisis de (fuerza y par, o "momento") que actúan sobre sistemas físicos que no experimentan una aceleración (a = 0), sino que están en equilibrio estático con su entorno. La aplicación de la segunda ley de Newton a un sistema da:
Donde la fuente en negrita indica un vector que tiene magnitud y dirección. 



La suma de fuerzas, una de las cuales puede ser desconocida, permite encontrar esa incógnita. Entonces, cuando está en equilibrio estático, la aceleración del sistema es cero y el sistema está en reposo o su centro de masa se mueve a velocidad constante. Asimismo, la aplicación del supuesto de aceleración cero a la suma de los momentos que actúan sobre el sistema conduce a:
Aquí, 


La suma de momentos, uno de los cuales puede ser desconocido, permite encontrar esa incógnita. Estas dos ecuaciones juntas se pueden aplicar para resolver hasta dos cargas (fuerzas y momentos) que actúan sobre el sistema.
De la primera ley de Newton, esto implica que la fuerza neta y el par neto en cada parte del sistema es cero. Las fuerzas netas iguales a cero se conocen como la primera condición de equilibrio, y el par neto igual a cero se conoce como la segunda condición de equilibrio. Véase estáticamente indeterminado.
Historia
Arquímedes (c. 287–c. 212 a. C.) realizó un trabajo pionero en estática. Los desarrollos posteriores en el campo de la estática se encuentran en las obras de Thebit.
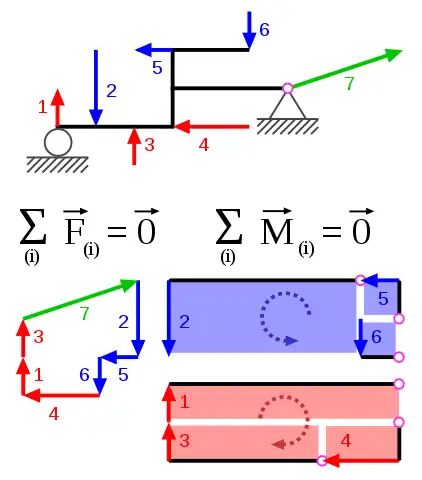
Vectores
Un escalar es una cantidad que solo tiene una magnitud, como masa o temperatura. Un vector tiene una magnitud y una dirección. Hay varias notaciones para identificar un vector, incluyendo:
- Un personaje de cara audaz V
- Un carácter subrayado V
- Un carácter con una flecha sobre él
.
Los vectores se suman usando la ley del paralelogramo o la ley del triángulo. Los vectores contienen componentes en bases ortogonales. Los vectores unitarios i, j y k están, por convención, a lo largo de los ejes x, y y z, respectivamente.
Fuerza
La fuerza es la acción de un cuerpo sobre otro. Una fuerza es un empujón o un tirón, y tiende a mover un cuerpo en la dirección de su acción. La acción de una fuerza se caracteriza por su magnitud, por la dirección de su acción y por su punto de aplicación. Así, la fuerza es una cantidad vectorial, porque su efecto depende tanto de la dirección como de la magnitud de la acción.
Las fuerzas se clasifican como fuerzas de contacto o de cuerpo. Una fuerza de contacto se produce por contacto físico directo; un ejemplo es la fuerza ejercida sobre un cuerpo por una superficie de apoyo. La fuerza de un cuerpo se genera en virtud de la posición de un cuerpo dentro de un campo de fuerza, como un campo gravitacional, eléctrico o magnético, y es independiente del contacto con cualquier otro cuerpo. Un ejemplo de una fuerza corporal es el peso de un cuerpo en el campo gravitacional de la Tierra.
Momento de una fuerza
Además de la tendencia a mover un cuerpo en la dirección de su aplicación, una fuerza también puede tender a girar un cuerpo alrededor de un eje. El eje puede ser cualquier línea que no corte ni sea paralela a la línea de acción de la fuerza. Esta tendencia rotacional se conoce como el momento (M) de la fuerza. El momento también se conoce como torque.
Momento sobre un punto
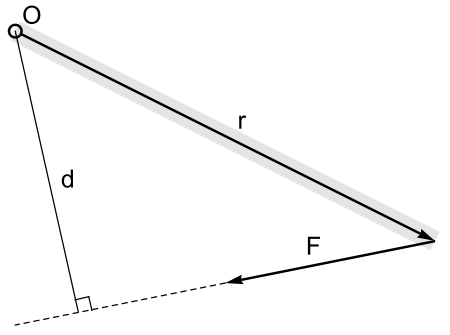
La magnitud del momento de una fuerza en un punto O, es igual a la distancia perpendicular de O a la línea de acción de F, multiplicada por la magnitud de la fuerza: M = F · d, dondeF = la fuerza aplicadad = la distancia perpendicular del eje a la línea de acción de la fuerza. Esta distancia perpendicular se llama brazo de momento.
La dirección del momento viene dada por la regla de la mano derecha, donde el sentido contrario a las agujas del reloj (CCW) está fuera de la página y el sentido de las agujas del reloj (CW) está dentro de la página. La dirección del momento puede tenerse en cuenta mediante el uso de una convención de signos establecida, como un signo más (+) para los momentos en el sentido contrario a las agujas del reloj y un signo menos (-) para los momentos en el sentido de las agujas del reloj, o viceversa. Los momentos se pueden sumar como vectores.
En formato vectorial, el momento se puede definir como el producto cruzado entre el vector de radio, r (el vector desde el punto O hasta la línea de acción), y el vector de fuerza, F:
Teorema de Varignon
El teorema de Varignon establece que el momento de una fuerza con respecto a cualquier punto es igual a la suma de los momentos de las componentes de la fuerza con respecto al mismo punto.
Ecuaciones de equilibrio
El equilibrio estático de una partícula es un concepto importante en estática. Una partícula está en equilibrio solo si la resultante de todas las fuerzas que actúan sobre la partícula es igual a cero. En un sistema de coordenadas rectangulares, las ecuaciones de equilibrio se pueden representar mediante tres ecuaciones escalares, donde las sumas de las fuerzas en las tres direcciones son iguales a cero. Una aplicación de ingeniería de este concepto es determinar las tensiones de hasta tres cables bajo carga, por ejemplo, las fuerzas ejercidas sobre cada cable de un polipasto que levanta un objeto o de cables de sujeción que sujetan un globo aerostático al suelo.
Momento de inercia
En la mecánica clásica, el momento de inercia, también llamado momento de masa, inercia rotacional, momento polar de inercia de masa o masa angular (unidades SI kg·m²) es una medida de la resistencia de un objeto a los cambios en su rotación. Es la inercia de un cuerpo giratorio con respecto a su rotación. El momento de inercia juega el mismo papel en la dinámica rotacional que la masa en la dinámica lineal, describiendo la relación entre el momento angular y la velocidad angular, el par y la aceleración angular, y varias otras cantidades. Los símbolos I y J se suelen utilizar para referirse al momento de inercia o momento polar de inercia.
Mientras que un tratamiento escalar simple del momento de inercia es suficiente para muchas situaciones, un tratamiento tensorial más avanzado permite el análisis de sistemas tan complicados como peonzas y movimiento giroscópico.
El concepto fue introducido por Leonhard Euler en su libro de 1765 Theoria motus corporum solidorum seu rigidorum; discutió el momento de inercia y muchos conceptos relacionados, como el eje principal de inercia.
Sólidos
La estática se utiliza en el análisis de estructuras, por ejemplo, en arquitectura e ingeniería estructural. La resistencia de los materiales es un campo relacionado de la mecánica que depende en gran medida de la aplicación del equilibrio estático. Un concepto clave es el centro de gravedad de un cuerpo en reposo: representa un punto imaginario en el que reside toda la masa de un cuerpo. La posición del punto con respecto a los cimientos sobre los que descansa un cuerpo determina su estabilidad en respuesta a fuerzas externas. Si el centro de gravedad existe fuera de los cimientos, entonces el cuerpo es inestable porque actúa un par: cualquier pequeña perturbación hará que el cuerpo se caiga o se vuelque. Si el centro de gravedad existe dentro de los cimientos, el cuerpo es estable ya que ningún par neto actúa sobre el cuerpo. Si el centro de gravedad coincide con los cimientos,
Fluidos
La hidrostática, también conocida como estática de fluidos, es el estudio de los fluidos en reposo (es decir, en equilibrio estático). La característica de cualquier fluido en reposo es que la fuerza ejercida sobre cualquier partícula del fluido es la misma en todos los puntos a la misma profundidad (o altitud) dentro del fluido. Si la fuerza neta es mayor que cero, el fluido se moverá en la dirección de la fuerza resultante. Este concepto fue formulado por primera vez en una forma ligeramente extendida por el matemático y filósofo francés Blaise Pascal en 1647 y se conoció como la Ley de Pascal. Tiene muchas aplicaciones importantes en hidráulica. Arquímedes, Abū Rayhān al-Bīrūnī, Al-Khazini y Galileo Galilei también fueron figuras importantes en el desarrollo de la hidrostática.
Contenido relacionado
Leptón
Estado termodinámico
Energía potencial electrostática






