Estadísticas de Bose-Einstein

format_list_bulleted Contenido keyboard_arrow_down

ImprimirCitar

Descripción del comportamiento de los bosons

En las estadísticas cuánticas, las estadísticas de Bose-Einstein (estadísticas B-E) describen una de las dos formas posibles en las que una colección de partículas indistinguibles que no interactúan puede ocupar un conjunto de estados de energía discretos disponibles en el equilibrio termodinámico. La agregación de partículas en el mismo estado, que es una característica de las partículas que obedecen a las estadísticas de Bose-Einstein, explica la corriente cohesiva de la luz láser y el deslizamiento sin fricción del helio superfluido. La teoría de este comportamiento fue desarrollada (1924-1925) por Satyendra Nath Bose, quien reconoció que una colección de partículas idénticas e indistinguibles se puede distribuir de esta manera. La idea fue posteriormente adoptada y ampliada por Albert Einstein en colaboración con Bose.

La estadística de Bose-Einstein se aplica solo a las partículas que no se limitan a una sola ocupación del mismo estado, es decir, partículas que no obedecen las restricciones del principio de exclusión de Pauli. Tales partículas tienen valores enteros de espín y se denominan bosones. Las partículas con giros semienteros se denominan fermiones y obedecen a la estadística de Fermi-Dirac.

Comparación de la ocupación promedio del estado terrestre para tres estadísticas

Distribución Bose-Einstein

A bajas temperaturas, los bosones se comportan de forma diferente a los fermiones (que obedecen a las estadísticas de Fermi-Dirac) de forma que un número ilimitado de ellos puede "condensarse" en el mismo estado de energía. Esta propiedad aparentemente inusual también da lugar al estado especial de la materia: el condensado de Bose-Einstein. Las estadísticas de Fermi-Dirac y Bose-Einstein se aplican cuando los efectos cuánticos son importantes y las partículas son "indistinguibles". Los efectos cuánticos aparecen si la concentración de partículas satisface

{displaystyle {frac {N}{V}}geq n_{q},}

donde $N$ es el número de partículas, $V$ es el volumen, y $n q$ es el concentración cuántica, para la cual la distancia entre partículas es igual a la longitud de onda térmica de De Broglie, de modo que las funciones de onda de las partículas apenas se superponen.

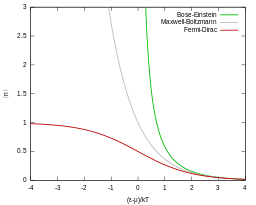
La estadística de Fermi-Dirac se aplica a los fermiones (partículas que obedecen el principio de exclusión de Pauli) y la estadística de Bose-Einstein se aplica a los bosones. Como la concentración cuántica depende de la temperatura, la mayoría de los sistemas a altas temperaturas obedecen al límite clásico (Maxwell-Boltzmann), a menos que también tengan una densidad muy alta, como en el caso de una enana blanca. Tanto Fermi-Dirac como Bose-Einstein se convierten en estadísticas de Maxwell-Boltzmann a alta temperatura o baja concentración.

Bose introdujo la estadística B–E para los fotones en 1924 y Einstein la generalizó a los átomos en 1924–25.

El número esperado de partículas en un estado de energía $i$ para las estadísticas B–E es:

${displaystyle {bar {n}}_{i}={frac {g_{i}}{e^{(varepsilon _{i}-mu)/k_{text{B}}T}-1}}}$

con $ε i ■ μ$ y dónde $n i$ es el número de ocupación (el número de partículas) en estado $i$ , $g_{i}$ es la degeneración del nivel energético $i$ , $ε i$ es la energía de la $i$ - estado, μ es el potencial químico (cero para un gas fotón), $k B$ es la constante de Boltzmann, y $T$ es la temperatura absoluta.

La diferencia de esta distribución $V(n)$ se calcula directamente de la expresión anterior para el número promedio.

{displaystyle V(n)=kT{frac {partial }{partial mu }}{bar {n}}_{i}=langle nrangle (1+langle nrangle)={bar {n}}+{bar {n}}^{2}}

Para comparación, el promedio de fermions con energía $varepsilon _{i}$ dada por Fermi-Dirac partícula-energía distribución tiene una forma similar:

{displaystyle {bar {n}}_{i}(varepsilon _{i})={frac {g_{i}}{e^{(varepsilon _{i}-mu)/k_{text{B}}T}+1}}.}

Como se mencionó anteriormente, tanto la distribución de Bose-Einstein como la distribución de Fermi-Dirac se aproximan a la distribución de Maxwell-Boltzmann en el límite de alta temperatura y baja densidad de partículas, sin necesidad de suposiciones ad hoc:

En el límite de baja densidad de partículas, ${displaystyle {bar {n}}_{i}={frac {g_{i}}{e^{(varepsilon _{i}-mu)/k_{text{B}}T}pm 1}}ll 1}$ , por lo tanto ${displaystyle e^{(varepsilon _{i}-mu)/k_{text{B}}T}pm 1gg 1}$ o equivalente ${displaystyle e^{(varepsilon _{i}-mu)/k_{text{B}}T}gg 1}$ . En ese caso, ${displaystyle {bar {n}}_{i}approx {frac {g_{i}}{e^{(varepsilon _{i}-mu)/k_{text{B}}T}}}={frac {1}{Z}}e^{-varepsilon _{i}/k_{text{B}}T}}$ , que es el resultado de las estadísticas de Maxwell-Boltzmann.
En el límite de alta temperatura, las partículas se distribuyen sobre una amplia gama de valores energéticos, por lo que la ocupación en cada estado (especialmente las altas energías con ${displaystyle varepsilon _{i}-mu gg k_{text{B}}T}$ ) es otra vez muy pequeño, ${displaystyle {bar {n}}_{i}={frac {g_{i}}{e^{(varepsilon _{i}-mu)/k_{text{B}}T}pm 1}}ll 1}$ . Esto reduce de nuevo a las estadísticas de Maxwell-Boltzmann.

Además de reducir a la distribución Maxwell-Boltzmann en el límite de alto $T$ y baja densidad, las estadísticas B-E también reducen a la distribución de leyes Rayleigh-Jeans para estados de baja energía con
${displaystyle varepsilon _{i}-mu ll k_{text{B}}T}$ , a saber

{displaystyle {begin{aligned}{bar {n}}_{i}&={frac {g_{i}}{e^{(varepsilon _{i}-mu)/k_{text{B}}T}-1}}\&approx {frac {g_{i}}{(varepsilon _{i}-mu)/k_{text{B}}T}}={frac {g_{i}k_{text{B}}T}{varepsilon _{i}-mu }}.end{aligned}}}

Historia

Władysław Natanson en 1911 concluyó que la ley de Planck requiere la indistinguibilidad de las 'unidades de energía', aunque no enmarcó esto en términos de los cuantos de luz de Einstein.

Mientras daba una conferencia en la Universidad de Dhaka (en lo que entonces era la India británica y ahora es Bangladesh) sobre la teoría de la radiación y la catástrofe ultravioleta, Satyendra Nath Bose pretendía mostrar a sus alumnos que la teoría contemporánea era inadecuada, porque predijo resultados que no estaban de acuerdo con los resultados experimentales. Durante esta conferencia, Bose cometió un error al aplicar la teoría, lo que inesperadamente dio una predicción que concordaba con el experimento. El error fue un simple error —similar a argumentar que lanzar dos monedas al aire arrojará dos caras la tercera parte de las veces— que parecería obviamente erróneo para cualquier persona con conocimientos básicos de estadística (sorprendentemente, este error se parecía al famoso error cometido por d& #39;Alembert conocido por su artículo Croix ou Pile). Sin embargo, los resultados que predijo coincidieron con el experimento, y Bose se dio cuenta de que, después de todo, podría no ser un error. Por primera vez, tomó la posición de que la distribución de Maxwell-Boltzmann no sería cierta para todas las partículas microscópicas en todas las escalas. Por lo tanto, estudió la probabilidad de encontrar partículas en varios estados en el espacio de fase, donde cada estado es un pequeño parche que tiene un volumen de fase de h³, y la posición y el momento de las partículas no se mantienen particularmente separadas sino que se consideran como una variable.

Bose adaptó esta conferencia en un breve artículo llamado 'La ley de Planck y la hipótesis de los cuantos de luz'. y lo envió a la Revista Filosófica. Sin embargo, el informe del árbitro fue negativo y el trabajo fue rechazado. Sin desanimarse, envió el manuscrito a Albert Einstein solicitando su publicación en el Zeitschrift für Physik. Einstein accedió de inmediato, tradujo personalmente el artículo del inglés al alemán (Bose había traducido anteriormente el artículo de Einstein sobre la teoría general de la relatividad del alemán al inglés) y se encargó de que se publicara. La teoría de Bose ganó respeto cuando Einstein envió su propio artículo en apoyo de la de Bose a Zeitschrift für Physik, pidiendo que se publiquen juntos. El artículo salió en 1924.

La razón por la que Bose produjo resultados precisos fue que, dado que los fotones son indistinguibles entre sí, no se pueden tratar dos fotones que tengan números cuánticos iguales (por ejemplo, vector de polarización y momento) como dos fotones identificables distintos. Por analogía, si en un universo alternativo las monedas se comportaran como fotones y otros bosones, la probabilidad de producir dos caras sería de hecho un tercio, y también lo es la probabilidad de obtener una cara y una cruz que es igual a la mitad para el monedas convencionales (clásicas, distinguibles). El "error" de Bose conduce a lo que ahora se llama estadísticas de Bose-Einstein.

Bose y Einstein extendieron la idea a los átomos y esto condujo a la predicción de la existencia de fenómenos que se conocieron como condensado de Bose-Einstein, una densa colección de bosones (que son partículas con espín entero, llamado así por Bose), que se demostró que existe mediante un experimento en 1995.

Derivación

Derivación del conjunto microcanónico

En el conjunto microcanónico, se considera un sistema con energía fija, volumen y número de partículas. Tomamos un sistema compuesto por ${textstyle N=sum _{i}n_{i}}$ Bosons idénticos, $n_{i}$ de los cuales tienen energía $varepsilon _{i}$ y se distribuyen $g_{i}$ niveles o estados con la misma energía $varepsilon _{i}$ , es decir. $g_{i}$ es la degeneración asociada con la energía $varepsilon _{i}$ energía total ${textstyle E=sum _{i}n_{i}varepsilon _{i}}$ . Cálculo del número de arreglos $n_{i}$ partículas distribuidas entre $g_{i}$ estados es un problema de combinatoria. Puesto que las partículas son indistinguibles en el contexto mecánico cuántico aquí, el número de formas para organizar $n_{i}$ partículas en $g_{i}$ cajas (para $i$ el nivel de energía) sería (ver imagen).

La imagen representa una posible distribución de partículas bosónicas en diferentes cajas. Las particiones de caja (verde) se pueden mover alrededor para cambiar el tamaño de las cajas y como resultado del número de bosones que cada caja puede contener.

{displaystyle w_{i,{text{BE}}}={frac {(n_{i}+g_{i}-1)!}{n_{i}!(g_{i}-1)!}}=C_{n_{i}}^{n_{i}+g_{i}-1},}

Donde ${displaystyle C_{k}^{m}}$ es la combinación k de un conjunto con m elementos. El número total de arreglos en un conjunto de bosons es simplemente el producto de los coeficientes binomiales ${displaystyle C_{n_{i}}^{n_{i}+g_{i}-1}}$ sobre todos los niveles de energía, es decir,

{displaystyle W_{text{BE}}=prod _{i}w_{i,{text{BE}}}=prod _{i}{frac {(n_{i}+g_{i}-1)!}{(g_{i}-1)!n_{i}!}},}

Número máximo de arreglos que determinan el número de ocupación correspondiente $n_{i}$ se obtiene maximizando la entropía, o equivalentemente, el ajuste ${displaystyle mathrm {d} (ln W_{text{BE}})=0}$ y teniendo en cuenta las condiciones ${textstyle N=sum n_{i},E=sum _{i}n_{i}varepsilon _{i}}$ en cuenta (como multiplicadores Lagrange). El resultado ${displaystyle n_{i}gg 1}$ , $g_{i}gg 1$ , ${displaystyle n_{i}/g_{i}=O(1)}$ es la distribución Bose-Einstein.

Derivación del gran conjunto canónico

La distribución de Bose-Einstein, que se aplica solo a un sistema cuántico de bosones que no interactúan, se deriva naturalmente del gran conjunto canónico sin aproximaciones. En este conjunto, el sistema es capaz de intercambiar energía e intercambiar partículas con un reservorio (temperatura T y potencial químico µ fijados por el reservorio).

Debido a la calidad de no interacción, cada nivel de partícula individual disponible (con nivel de energía ϵ) forma un sistema termodinámico separado en contacto con el depósito. Es decir, el número de partículas dentro del sistema general que ocupan un estado de partícula individual determinado forman un subconjunto que también es un gran conjunto canónico; por lo tanto, puede analizarse mediante la construcción de una gran función de partición.

Cada estado de partículas es de una energía fija, $varepsilon$ . Dado que el sub-ensemble asociado con un estado de partículas individuales varía únicamente por el número de partículas, está claro que la energía total del sub-ensemble también es directamente proporcional al número de partículas en el estado de una sola partícula; donde $N$ es el número de partículas, la energía total del sub-ensemble será entonces ${displaystyle Nvarepsilon }$ . Comenzando con la expresión estándar para una gran función de partición y reemplazando $E$ con ${displaystyle Nvarepsilon }$ , la función de partición grande toma el formulario

{displaystyle {mathcal {Z}}=sum _{N}exp((Nmu -Nvarepsilon)/k_{text{B}}T)=sum _{N}exp(N(mu -varepsilon)/k_{text{B}}T)}

Esta fórmula se aplica tanto a los sistemas fermiónicos como a los sistemas bosónicos. La estadística de Fermi-Dirac surge cuando se considera el efecto del principio de exclusión de Pauli: mientras que el número de fermiones que ocupan el mismo estado de una sola partícula solo puede ser 1 o 0, el número de bosones que ocupan un solo estado de partícula puede ser cualquier número entero. Por lo tanto, la función de gran partición para los bosones se puede considerar una serie geométrica y se puede evaluar como tal:

{displaystyle {begin{aligned}{mathcal {Z}}&=sum _{N=0}^{infty }exp(N(mu -varepsilon)/k_{text{B}}T)=sum _{N=0}^{infty }[exp((mu -varepsilon)/k_{text{B}}T)]^{N}\&={frac {1}{1-exp((mu -varepsilon)/k_{text{B}}T)}}.end{aligned}}}

Tenga en cuenta que la serie geométrica es convergente sólo si $<math alttext="{displaystyle e^{(mu -varepsilon)/k_{text{B}}T}e()μ μ − − ε ε )/kBT.1{displaystyle e^{(mu -varepsilon)/k_{text{B}T}traducido1}<img alt="{displaystyle e^{(mu -varepsilon)/k_{text{B}}T}$ , incluido el caso en que $epsilon = 0$ . Esto implica que el potencial químico para el gas Bose debe ser negativo, es decir, $<math alttext="{displaystyle mu μ μ .0{displaystyle mu = 0} <img alt="{displaystyle mu$ , mientras que el gas Fermi se permite tomar valores tanto positivos como negativos para el potencial químico.

El número promedio de partículas para ese subestado de una sola partícula viene dado por

{displaystyle langle Nrangle =k_{text{B}}T{frac {1}{mathcal {Z}}}left({frac {partial {mathcal {Z}}}{partial mu }}right)_{V,T}={frac {1}{exp((varepsilon -mu)/k_{text{B}}T)-1}}}

La diferencia en el número de partículas, ${textstyle sigma _{N}^{2}=langle N^{2}rangle -langle Nrangle ^{2}}$ , es:

{displaystyle sigma _{N}^{2}=k_{text{B}}Tleft({frac {dlangle Nrangle }{dmu }}right)_{V,T}={frac {exp((varepsilon -mu)/k_{text{B}}T)}{(exp((varepsilon -mu)/k_{text{B}}T)-1)^{2}}}=langle Nrangle (1+langle Nrangle).}

Como resultado, para los estados altamente ocupados la desviación estándar del número de partículas de un nivel energético es muy grande, ligeramente mayor que el número de partículas en sí mismo: ${displaystyle sigma _{N}approx langle Nrangle }$ . Esta gran incertidumbre se debe al hecho de que la distribución de probabilidad para el número de bosones en un nivel de energía dado es una distribución geométrica; algo contraintuitivamente, el valor más probable para N es siempre 0. (En contraste, las partículas clásicas tienen en su lugar una distribución Poisson en número de partículas para un estado dado, con una incertidumbre mucho menor de ${textstyle sigma _{N,{rm {classical}}}={sqrt {langle Nrangle }}}$ , y con la más probable N valor estar cerca $langle Nrangle$ .)

Derivación en el enfoque canónico

También es posible obtener estadísticas aproximadas de Bose-Einstein en el conjunto canónico. Estas derivaciones son largas y solo dan los resultados anteriores en el límite asintótico de un gran número de partículas. La razón es que el número total de bosones está fijo en el conjunto canónico. La distribución de Bose-Einstein en este caso se puede derivar como en la mayoría de los textos por maximización, pero la mejor derivación matemática es por el método de Darwin-Fowler de valores medios como lo enfatiza Dingle. Véase también Müller-Kirsten. Sin embargo, las fluctuaciones del estado fundamental en la región condensada son marcadamente diferentes en los conjuntos canónico y grancanónico.

Derivación

Supongamos que tenemos un número de niveles de energía, etiquetados por índice $i$ , cada nivel que tiene energía ${displaystyle varepsilon _{i}}$ y con un total de ${displaystyle n_{i}}$ partículas. Suponga que cada nivel contiene ${displaystyle g_{i}}$ subnivels distintos, todos los cuales tienen la misma energía, y que son distinguibles. Por ejemplo, dos partículas pueden tener diferente momenta, en cuyo caso se distinguen entre sí, pero todavía pueden tener la misma energía. El valor de ${displaystyle g_{i}}$ asociado con el nivel $i$ se llama "degeneración" de ese nivel energético. Cualquier número de bosones puede ocupar el mismo subnivel.

Vamos ${displaystyle w(n,g)}$ ser el número de formas de distribución $n$ partículas entre las $g$ subnivels of an energy level. Sólo hay una manera de distribuir $n$ particles with one sublevel, therefore ${displaystyle w(n,1)=1}$ . Es fácil ver que hay ${displaystyle (n+1)}$ maneras de distribuir $n$ partículas en dos subnivels que escribiremos como:

{displaystyle w(n,2)={frac {(n+1)!}{n!1!}}.}

Con un poco de pensamiento (ver Notas abajo) se puede ver que el número de maneras de distribuir $n$ partículas en tres subnivel

{displaystyle w(n,3)=w(n,2)+w(n-1,2)+cdots +w(1,2)+w(0,2)}

así

{displaystyle w(n,3)=sum _{k=0}^{n}w(n-k,2)=sum _{k=0}^{n}{frac {(n-k+1)!}{(n-k)!1!}}={frac {(n+2)!}{n!2!}}}

donde hemos utilizado lo siguiente theorem con coeficientes binomiales:

{displaystyle sum _{k=0}^{n}{frac {(k+a)!}{k!a!}}={frac {(n+a+1)!}{n!(a+1)!}}.}

Continuando este proceso, podemos ver que ${displaystyle w(n,g)}$ es sólo un coeficiente binomio (Véanse las notas a continuación)

{displaystyle w(n,g)={frac {(n+g-1)!}{n!(g-1)!}}.}

Por ejemplo, el número de población de dos partículas en tres subnivel es de 200, 110, 101, 020, 011, o 002 para un total de seis que equivale a 4!/(2!2!). Número de formas que un conjunto de números de ocupación ${displaystyle n_{i}}$ se puede realizar es el producto de las maneras en que cada nivel de energía individual puede ser poblado:

{displaystyle W=prod _{i}w(n_{i},g_{i})=prod _{i}{frac {(n_{i}+g_{i}-1)!}{n_{i}!(g_{i}-1)!}}approx prod _{i}{frac {(n_{i}+g_{i})!}{n_{i}!(g_{i})!}}}

donde la aproximación asume que $n_{i}gg 1$ .

Siguiendo el mismo procedimiento utilizado en la conducción de las estadísticas Maxwell-Boltzmann, deseamos encontrar el conjunto de ${displaystyle n_{i}}$ para la cual W se maximiza, sujeto a la restricción de que haya un número total fijo de partículas, y una energía total fija. La máxima de $W$ y ${displaystyle ln(W)}$ ocurre al mismo valor ${displaystyle n_{i}}$ y, ya que es más fácil de lograr matemáticamente, maximizaremos la última función en su lugar. Limitamos nuestra solución utilizando multiplicadores Lagrange formando la función:

{displaystyle f(n_{i})=ln(W)+alpha (N-sum n_{i})+beta (E-sum n_{i}varepsilon _{i})}

Usando el $n_{i}gg 1$ aproximación y uso de la aproximación de Stirling para los factoriales $left(x!approx x^{x},e^{-x},{sqrt {2pi x}}right)$ da

{displaystyle f(n_{i})=sum _{i}(n_{i}+g_{i})ln(n_{i}+g_{i})-n_{i}ln(n_{i})+alpha left(N-sum n_{i}right)+beta left(E-sum n_{i}varepsilon _{i}right)+K.}

Donde K es la suma de una serie de términos que no son funciones de la $n_{i}$ . Tomar el derivado con respecto a ${displaystyle n_{i}}$ , y establecer el resultado a cero y resolver para ${displaystyle n_{i}}$ , produce el número de población Bose-Einstein:

{displaystyle n_{i}={frac {g_{i}}{e^{alpha +beta varepsilon _{i}}-1}}.}

Por un proceso similar al descrito en el artículo de estadísticas Maxwell-Boltzmann, se puede ver que:

{displaystyle dln W=alpha ,dN+beta ,dE}

que, usando la famosa relación de Boltzmann ${displaystyle S=k_{text{B}},ln W}$ se convierte en una declaración de la segunda ley de la termodinámica a volumen constante, y sigue que ${displaystyle beta ={frac {1}{k_{text{B}}T}}}$ y ${displaystyle alpha =-{frac {mu }{k_{text{B}}T}}}$ Donde S es la entropía, $mu$ es el potencial químico, k_B es la constante de Boltzmann y T es la temperatura, por lo que finalmente:

{displaystyle n_{i}={frac {g_{i}}{e^{(varepsilon _{i}-mu)/k_{text{B}}T}-1}}.}

Tenga en cuenta que la fórmula anterior se escribe a veces:

{displaystyle n_{i}={frac {g_{i}}{e^{varepsilon _{i}/k_{text{B}}T}/z-1}},}

Donde ${displaystyle z=exp(mu /k_{text{B}}T)}$ es la actividad absoluta, como señaló McQuarrie.

Observe también que cuando los números de partículas no se conservan, eliminar la conservación de la limitación de números de partículas es equivalente a establecer $alpha$ y, por consiguiente, el potencial químico $mu$ a cero. Este será el caso de fotones y partículas masivas en equilibrio mutuo y la distribución resultante será la distribución Planck.

Notas

Una manera mucho más simple de pensar en la función de distribución Bose-Einstein es considerar que n partículas son denotadas por bolas idénticas y g shells están marcados por particiones de línea g-1. Está claro que las permutaciones de estos bolas y g - 1 particiones dará diferentes formas de organizar bosons en diferentes niveles de energía. Digamos, por 3 (=n) partículas y 3 (=g) shells, therefore ()g −1) = 2, el arreglo podría ser Silencio●, o Silencio, o Silencio● , etc. De ahí el número de permutaciones distintas n +g −1) objetos que tienen n Artículos idénticos y (g− 1) artículos idénticos serán:

{displaystyle {frac {(g-1+n)!}{(g-1)!n!}}}

Vea la imagen para una representación visual de una tal distribución de n partículas en g cajas que pueden ser representadas g − 1 particiones.

El propósito de estas notas es aclarar algunos aspectos de la derivación de la distribución Bose-Einstein (B-E) para principiantes. La enumeración de casos (o formas) en la distribución B-E puede retransmitirse de la siguiente manera. Considere un juego de dados tirando en el que hay $n$ dados, con cada muerte tomando valores en el set ${displaystyle {1,dotsg}}$ , para $ggeq 1$ . Las limitaciones del juego son que el valor de una muerte $i$ , denotado por ${displaystyle m_{i}}$ , tiene que ser mayor o igual a el valor de la muerte ${displaystyle (i-1)}$ , denotado por ${displaystyle m_{i-1}}$ En el lanzamiento anterior, es decir, $m_{i}geq m_{i-1}$ . Por lo tanto, una secuencia válida de tiros de la muerte puede ser descrita por un n-tuple ${displaystyle (m_{1},m_{2},dotsm_{n})}$ , tal que $m_{i}geq m_{i-1}$ . Vamos ${displaystyle S(n,g)}$ denota el conjunto de estos válidos n-tuples:

{displaystyle S(n,g)=left{(m_{1},m_{2},dotsm_{n}),{Big |},m_{i}geq m_{i-1},m_{i}in left{1,ldotsgright},forall i=1,dotsnright}.}

()1)

Entonces la cantidad ${displaystyle w(n,g)}$ (definido anteriormente como el número de formas de distribuir $n$ partículas entre las $g$ subnivels of an energy level) es el cardenality of ${displaystyle S(n,g)}$ , es decir, el número de elementos (o válidos n-tuples) ${displaystyle S(n,g)}$ . Así el problema de encontrar una expresión para ${displaystyle w(n,g)}$ se convierte en el problema de contar los elementos en ${displaystyle S(n,g)}$ .

Ejemplo n = 4, g = 3:

{displaystyle S(4,3)=left{underbrace {(1111),(1112),(1113)} _{(a)},underbrace {(1122),(1123),(1133)} _{(b)},underbrace {(1222),(1223),(1233),(1333)} _{(c)},underbrace {(2222),(2223),(2233),(2333),(3333)} _{(d)}right}}

{displaystyle w(4,3)=15}

(hay

15

elementos en

{displaystyle S(4,3)}

)

Subset ${displaystyle (a)}$ se obtiene mediante la fijación de todos los índices ${displaystyle m_{i}}$ a $1$ , excepto por el último índice, ${displaystyle m_{n}}$ , que se incrementa de $1$ a ${displaystyle g=3}$ . Subset $(b)$ se obtiene mediante fijación ${displaystyle m_{1}=m_{2}=1}$ , y aumento ${displaystyle m_{3}}$ desde ${displaystyle 2}$ a ${displaystyle g=3}$ . Debido a la limitación ${displaystyle m_{i}geq m_{i-1}}$ sobre los índices ${displaystyle S(n,g)}$ , el índice ${displaystyle m_{4}}$ debe tomar automáticamente valores ${displaystyle left{2,3right}}$ . La construcción de subconjuntos ${displaystyle (c)}$ y ${displaystyle (d)}$ sigue de la misma manera.

Cada elemento ${displaystyle S(4,3)}$ puede ser pensado como un multiconjunto de la cardenalidad ${displaystyle n=4}$ ; los elementos de este multiset se toman del conjunto ${displaystyle left{1,2,3right}}$ de la cardinalidad ${displaystyle g=3}$ , y el número de tales multiconjuntos es el coeficiente multiconjunto

{displaystyle leftlangle {begin{matrix}3\4end{matrix}}rightrangle ={3+4-1 choose 3-1}={3+4-1 choose 4}={frac {6!}{4!2!}}=15}

Más generalmente, cada elemento de ${displaystyle S(n,g)}$ es un multiconjunto de cardenalidad $n$ (número de dados) con elementos tomados del conjunto ${displaystyle left{1,dotsgright}}$ de la cardinalidad $g$ (número de posibles valores de cada muerte), y el número de tales múltiples conjuntos, es decir, ${displaystyle w(n,g)}$ es el coeficiente multiset

{displaystyle w(n,g)=leftlangle {begin{matrix}g\nend{matrix}}rightrangle ={g+n-1 choose g-1}={g+n-1 choose n}={frac {(g+n-1)!}{n!(g-1)!}}}

()2)

que es exactamente igual a la fórmula para ${displaystyle w(n,g)}$ , como se deriva arriba con la ayuda de un teorema que implica coeficientes binomiales, a saber

{displaystyle sum _{k=0}^{n}{frac {(k+a)!}{k!a!}}={frac {(n+a+1)!}{n!(a+1)!}}.}

()3)

Para entender la descomposición

{displaystyle w(n,g)=sum _{k=0}^{n}w(n-k,g-1)=w(n,g-1)+w(n-1,g-1)+dots +w(1,g-1)+w(0,g-1)}

()4)

o por ejemplo, ${displaystyle n=4}$ y ${displaystyle g=3}$

{displaystyle w(4,3)=w(4,2)+w(3,2)+w(2,2)+w(1,2)+w(0,2),}

vamos a reorganizar los elementos ${displaystyle S(4,3)}$ como sigue:

{displaystyle S(4,3)=left{underbrace {(1111),(1112),(1122),(1222),(2222)} _{(alpha)},underbrace {(111{color {Red}{underset {=}{3}}}),(112{color {Red}{underset {=}{3}}}),(122{color {Red}{underset {=}{3}}}),(222{color {Red}{underset {=}{3}}})} _{(beta)},underbrace {(11{color {Red}{underset {==}{33}}}),(12{color {Red}{underset {==}{33}}}),(22{color {Red}{underset {==}{33}}})} _{(gamma)},underbrace {(1{color {Red}{underset {===}{333}}}),(2{color {Red}{underset {===}{333}}})} _{(delta)}underbrace {({color {Red}{underset {====}{3333}}})} _{(omega)}right}.}

Claramente, el subconjunto ${displaystyle (alpha)}$ de ${displaystyle S(4,3)}$ es el mismo que el conjunto

{displaystyle S(4,2)=left{(1111),(1112),(1122),(1222),(2222)right}.}

Eliminando el índice ${displaystyle m_{4}=3}$ (shown in rojo con doble subrayado) en el subconjunto $(beta)$ de ${displaystyle S(4,3)}$ , uno obtiene el conjunto

{displaystyle S(3,2)=left{(111),(112),(122),(222)right}.}

En otras palabras, hay una correspondencia entre el subconjunto $(beta)$ de ${displaystyle S(4,3)}$ y el conjunto ${displaystyle S(3,2)}$ . Escribimos

{displaystyle (beta)longleftrightarrow S(3,2).}

Del mismo modo, es fácil ver que

{displaystyle (gamma)longleftrightarrow S(2,2)=left{(11),(12),(22)right}}

{displaystyle (delta)longleftrightarrow S(1,2)=left{(1),(2)right}}

{displaystyle (omega)longleftrightarrow S(0,2)={}=varnothing.}

Así podemos escribir

{displaystyle S(4,3)=bigcup _{k=0}^{4}S(4-k,2)}

o más generalmente,

{displaystyle S(n,g)=bigcup _{k=0}^{n}S(n-k,g-1);}

()5)

y desde los juegos

{displaystyle S(i,g-1),{text{ for }}i=0,dotsn}

no son de interés, así que tenemos

{displaystyle w(n,g)=sum _{k=0}^{n}w(n-k,g-1),}

()6)

con la convención que

{displaystyle w(0,g)=1\forall g,{text{ and }}w(n,0)=1\forall n.}

()7)

Continuando el proceso, llegamos a la siguiente fórmula

{displaystyle w(n,g)=sum _{k_{1}=0}^{n}sum _{k_{2}=0}^{n-k_{1}}w(n-k_{1}-k_{2},g-2)=sum _{k_{1}=0}^{n}sum _{k_{2}=0}^{n-k_{1}}cdots sum _{k_{g}=0}^{n-sum _{j=1}^{g-1}k_{j}}w(n-sum _{i=1}^{g}k_{i},0).}

Uso de la convención (7)₂ arriba, obtenemos la fórmula

{displaystyle w(n,g)=sum _{k_{1}=0}^{n}sum _{k_{2}=0}^{n-k_{1}}cdots sum _{k_{g}=0}^{n-sum _{j=1}^{g-1}k_{j}}1,}

()8)

teniendo en cuenta eso $q$ y $p$ siendo constantes, tenemos

{displaystyle sum _{k=0}^{q}p=qp.}

()9)

A continuación se puede verificar que (8) y (2) dan el mismo resultado para ${displaystyle w(4,3)}$ , $w(3,3)$ , ${displaystyle w(3,2)}$ , etc.

Aplicaciones interdisciplinarias

Vista como una distribución de probabilidad pura, la distribución de Bose-Einstein ha encontrado aplicación en otros campos:

En los últimos años, las estadísticas de Bose-Einstein también se han utilizado como método de ponderación a plazo en la recuperación de información. El método es uno de una colección de modelos DFR ("Divergence From Randomness"), siendo la noción básica que las estadísticas Bose-Einstein pueden ser un indicador útil en los casos en que un término particular y un documento particular tienen una relación significativa que no habría ocurrido puramente por casualidad. El código fuente para la aplicación de este modelo está disponible en el proyecto Terrier de la Universidad de Glasgow.
La evolución de muchos sistemas complejos, incluyendo la World Wide Web, las redes de negocios y citación, está codificada en la web dinámica que describe las interacciones entre los componentes del sistema. A pesar de su carácter irreversible y noquilibrio, estas redes siguen estadísticas de Bose y pueden someterse a condensación de Bose-Einstein. Abordar las propiedades dinámicas de estos sistemas de noquilibrio en el marco de los gases cuánticos equilibrios predice que los fenómenos "primer mover-advantage", "fit-get-rich" (FGR) y "ganner-takes-all" observados en sistemas competitivos son fases termodinámicamente distintas de las redes evolutivas subyacentes.

Contenido relacionado

Más resultados...