Estadística de pedidos

Funciones de densidad de probabilidad de las estadísticas de pedido para una muestra de tamaño n= 5 de una distribución exponencial con parámetro de escala unitaria

En estadística, la késima estadística de orden de una muestra estadística es igual a su késimo valor más pequeño. Junto con las estadísticas de rango, las estadísticas de orden se encuentran entre las herramientas más fundamentales en las estadísticas e inferencias no paramétricas.

Los casos especiales importantes de las estadísticas de orden son el valor mínimo y máximo de una muestra y (con algunas calificaciones que se analizan a continuación) la mediana de la muestra y otros cuantiles de la muestra.

Cuando se usa la teoría de la probabilidad para analizar estadísticas de orden de muestras aleatorias de una distribución continua, la función de distribución acumulativa se usa para reducir el análisis al caso de estadísticas de orden de la distribución uniforme.

Notación y ejemplos

Por ejemplo, suponga que se observan o registran cuatro números, lo que da como resultado una muestra de tamaño 4. Si los valores de la muestra son

6, 9, 3, 8,

las estadísticas del pedido se denotarían

x()1)=3,x()2)=6,x()3)=8,x()4)=9,{displaystyle x_{(1)}=3, x_{(2)}=6,\ x_{(3)}=8,\ x_{(4)}=9,,}

donde el subíndice (i) entre paréntesis indica iésimo orden de la muestra.

La estadística de primer orden (o estadística de menor orden) es siempre el mínimo de la muestra, es decir,

X()1)=min{}X1,...... ,Xn}{displaystyle X_{(1)}=min{,X_{1},ldotsX_{n},}}

donde, siguiendo una convención común, usamos letras mayúsculas para referirnos a variables aleatorias y letras minúsculas (como arriba) para referirnos a sus valores reales observados.

Del mismo modo, para una muestra de tamaño n, el nestadística de orden ésimo (o estadística de orden más grande) es el máximo, es decir,

X()n)=max{}X1,...... ,Xn}.{displaystyle X_{(n)}=max{,X_{1},ldotsX_{n},}

El rango de muestra es la diferencia entre el máximo y el mínimo. Es una función de las estadísticas del pedido:

Range{}X1,...... ,Xn}=X()n)− − X()1).{displaystyle {rm {fnMicrosoft Sans Serif}fnMicrosoft Sans X_{n},}=X_{(n)}-X_{(1)}

Una estadística importante similar en el análisis exploratorio de datos que está simplemente relacionada con las estadísticas de orden es el rango intercuartílico de la muestra.

La mediana muestra puede o no ser una estadística de pedido, ya que hay un solo valor medio sólo cuando el número n de observaciones es extraño. Más precisamente, si n = 2m+ 1 para algunos enteros m, entonces la mediana muestra es X()m+1){displaystyle X_{(m+1)} y también es una estadística de orden. Por otro lado, cuando n es incluso, n = 2m y hay dos valores medios, X()m){displaystyle X_{(m)} y X()m+1){displaystyle X_{(m+1)}, y el medio de muestra es una función de los dos (normalmente el promedio) y por lo tanto no una estadística de orden. Se aplican comentarios similares a todos los quantiles de muestra.

Análisis probabilístico

Dadas las variables aleatorias X₁, X₂..., X_n, las estadísticas del pedido X₍₁₎, X₍₂₎,..., X _(n) también son variables aleatorias, definidas ordenando los valores (realizaciones) de X₁,..., X_n en orden creciente.

Cuando las variables aleatorias X₁, X₂..., X_n forman una muestra, son independientes e idénticamente distribuidas. Este es el caso que se trata a continuación. En general, las variables aleatorias X₁,..., X_n pueden surgir al tomar muestras de más de una población. Entonces son independientes, pero no necesariamente distribuidos de manera idéntica, y su distribución de probabilidad conjunta está dada por el teorema de Bapat-Beg.

A partir de ahora, supondremos que las variables aleatorias consideradas son continuas y, cuando sea conveniente, también supondremos que tienen una función de densidad de probabilidad (PDF), es decir, son absolutamente continuas. Las peculiaridades del análisis de distribuciones asignando masa a puntos (en particular, distribuciones discretas) se discuten al final.

Función de distribución acumulativa de estadísticas de pedidos

Para una muestra aleatoria como arriba, con distribución acumulativa FX()x){displaystyle F_{X}(x)}, las estadísticas de pedido para esa muestra tienen distribuciones acumuladas como sigue (donde) r especifica qué orden estadística:

FX()r)()x)=.. j=rn()nj)[FX()x)]j[1− − FX()x)]n− − j{displaystyle F_{X_{(r)}(x)=sum _{j=r}{n}{binom} [n}{j} [F_{X}(x)]^{j}[1-F_{X}(x)]^{n-j}

La función de densidad de probabilidad correspondiente se puede derivar de este resultado y se encuentra que es

fX()r)()x)=n!()r− − 1)!()n− − r)!fX()x)[FX()x)]r− − 1[1− − FX()x)]n− − r.{displaystyle f_{X_{(r)}(x)={frac {n!}{(r-1)!(n-r)}}f_{X}(x)[F_{X}(x)}{r-1}[1-F_{X}(x)}{n-r}}.

Además, hay dos casos especiales, que tienen CDF que son fáciles de calcular.

FX()n)()x)=Prob⁡ ⁡ ()max{}X1,...... ,Xn}≤ ≤ x)=[FX()x)]n[displaystyle F_{X_{(n)}}(x)=operatorname {Prob} (max{\,X_{1},ldotsX_{n},}leq x)=[F_{X}(x)]^{n}}}

FX()1)()x)=Prob⁡ ⁡ ()min{}X1,...... ,Xn}≤ ≤ x)=1− − [1− − FX()x)]n{displaystyle F_{X_{(1)}(x)=operatorname {Prob} (min{\,X_{1},ldotsX_{n},}leq x)=1-[1-F_{X}(x)}{n}}}}}} {n}n}n}

Que se puede derivar mediante una cuidadosa consideración de las probabilidades.

Distribuciones de probabilidad de estadísticas de pedidos

Estadísticas de pedidos muestreadas a partir de una distribución uniforme

En esta sección mostramos que los estadísticos de orden de la distribución uniforme en el intervalo unitario tienen distribuciones marginales pertenecientes a la familia de distribuciones beta. También proporcionamos un método simple para derivar la distribución conjunta de cualquier número de estadísticos de orden y, finalmente, traducir estos resultados a distribuciones continuas arbitrarias utilizando la cdf.

Asumimos en toda esta sección que X1,X2,...... ,Xn{displaystyle X_{1},X_{2},ldots X_{n} es una muestra aleatoria extraída de una distribución continua con cdf FX{displaystyle F_{X}. Denotación Ui=FX()Xi){displaystyle U_{i}=F_{X}(X_{i}} obtenemos la muestra aleatoria correspondiente U1,...... ,Un{displaystyle U_{1},ldots U_{n} de la distribución uniforme estándar. Tenga en cuenta que las estadísticas de pedido también satisfacen U()i)=FX()X()i)){displaystyle U_{(i)}=F_{X}(X_{(i)}}.

La función de densidad de probabilidad de la estadística del orden U()k){displaystyle U_{(k)} es igual a

fU()k)()u)=n!()k− − 1)!()n− − k)!uk− − 1()1− − u)n− − k{displaystyle f_{U_{(k)}(u)={n! over (k-1)!(n-k)}u^{k-1}(1-u)^{n-k}

es decir, el estadístico de orden k de la distribución uniforme es una variable aleatoria con distribución beta.

U()k)♪ ♪ Beta⁡ ⁡ ()k,n+1− − k).{displaystyle U_{(k)}sim operatorname {Beta} (k,n+1mathbf {-} k).}

La prueba de estas declaraciones es la siguiente. Para U()k){displaystyle U_{(k)} estar entre u y u+du, es necesario que exactamente k− 1 elementos de la muestra son más pequeños que u, y que al menos uno es entre u y u+ du. La probabilidad de que más de uno esté en este último intervalo ya es O()du2){displaystyle O(du^{2}}, así que tenemos que calcular la probabilidad de que exactamente k− 1, 1 y n−k las observaciones caen en los intervalos ()0,u){displaystyle (0,u)}, ()u,u+du){displaystyle (u,u+du)} y ()u+du,1){displaystyle (u+du,1)} respectivamente. Esto es igual (consultar la distribución multinomial para detalles)

n!()k− − 1)!()n− − k)!uk− − 1⋅ ⋅ du⋅ ⋅ ()1− − u− − du)n− − k{displaystyle {n! over (k-1)! (n-k)}u^{k-1}cdot ducdot (1-u-du)^{n-k}

y el resultado sigue.

La media de esta distribución es k / (n + 1).

La distribución conjunta de las estadísticas de orden de la distribución uniforme

Del mismo modo, para i < j, la función de densidad de probabilidad conjunta de las estadísticas de dos órdenes U_(i) < Se puede demostrar que U_(j) es

fU()i),U()j)()u,v)=n!ui− − 1()i− − 1)!()v− − u)j− − i− − 1()j− − i− − 1)!()1− − v)n− − j()n− − j)!{displaystyle f_{U_{(i)},U_{(j)}(u,v)=n!{u^{i-1} over (i-1)}{(v-u)^{j-i-1} over (j-i-1)}{(1-v)^{n-j} over (n-j)}}}}}} {

que es (hasta términos de orden superior que O()dudv){displaystyle O(du,dv)}) la probabilidad de que i− 1, j− 1 −i, 1 y n−j elementos de muestra caen en los intervalos ()0,u){displaystyle (0,u)}, ()u,u+du){displaystyle (u,u+du)}, ()u+du,v){displaystyle (u+du,v)}, ()v,v+dv){displaystyle (v,v+dv)}, ()v+dv,1){displaystyle (v+dv,1)} respectivamente.

Uno razona de una manera totalmente análoga para derivar las distribuciones conjuntas de orden superior. Quizás sorprendentemente, la densidad conjunta de las estadísticas de orden n resulta ser constante:

fU()1),U()2),...... ,U()n)()u1,u2,...... ,un)=n!.{displaystyle f_{U_{(1)},U_{(2)},ldotsU_{(n)}(u_{1},u_{2},ldotsu_{n})=n!}

Una manera de entender esto es que la muestra no ordenada tiene densidad constante igual a 1, y que hay n! diferentes permutaciones de la muestra correspondientes a la misma secuencia de estadísticas del orden. Esto se relaciona con el hecho de que 1/n! es el volumen de la región <math alttext="{displaystyle 0<u_{1}<cdots <u_{n}0.u1.⋯ ⋯ .un.1{displaystyle 0 0 0 0 0 0 0 0} 0cdots<img alt="0<u_{1}<cdots <u_{n}. También está relacionado con otra particularidad de estadísticas de orden de variables aleatorias uniformes: De la calidad BRS se desprende que el número máximo esperado de variables uniformes U(0,1] aleatorias se puede elegir de una muestra de tamaño n con una suma no superior <math alttext="{displaystyle 0<s0.s.n/2{displaystyle 0 hechos realizados/2}<img alt="{displaystyle 0<s está obligado por encima 2sn{displaystyle {sqrt {2sn}}, que es invariable en el conjunto de todos s,n{displaystyle s,n}con producto constante sn{displaystyle sn}.

Utilizando las fórmulas anteriores, se puede derivar la distribución del rango de las estadísticas de pedidos, es decir, la distribución de U()n)− − U()1){displaystyle U_{(n)}-U_{(1)}, es decir, máximo menos el mínimo. Más generalmente, para jgeq 1}" xmlns="http://www.w3.org/1998/Math/MathML">n≥ ≥ k■j≥ ≥ 1{displaystyle ngeq k confianzajgeq 1}jgeq 1}" aria-hidden="true" class="mwe-math-fallback-image-inline" src="https://wikimedia.org/api/rest_v1/media/math/render/svg/c6e69b8e86122c4678c3b97d6ebb6f0f451add78" style="vertical-align: -0.671ex; width:14.022ex; height:2.509ex;"/>, U()k)− − U()j){displaystyle U_{(k)}-U_{(j)} también tiene una distribución beta:

U()k)− − U()j)♪ ♪ Beta⁡ ⁡ ()k− − j,n− − ()k− − j)+1){displaystyle U_{(k)}-U_{(j)}sim operatorname {Beta} (k-j,n-(k-j)+1)}

Cov⁡ ⁡ ()U()k),U()j))=j()n− − k+1)()n+1)2()n+2){displaystyle operatorname {Cov} (U_{(k)},U_{(j)})={frac {j(n-k+1)}{(n+1)} {c}}}}} {}}} {fn+2}}}}}} {f}}} {cH00}}}} {cH00}}}}}} {f}}}}}} {f}}}}}} {f}}}}} {f}}} {f}}}}}}} {f}}} {f}}}}} {f}}}}}}}}}}} {f}}}}}}}}} {f}} {f}}}}}}}}}}}}} {f}}}}}}}}}

Var⁡ ⁡ ()U()k)− − U()j))=Var⁡ ⁡ ()U()k))+Var⁡ ⁡ ()U()j))− − 2⋅ ⋅ Cov⁡ ⁡ ()U()k),U()j))=k()n− − k+1)()n+1)2()n+2)+j()n− − j+1)()n+1)2()n+2)− − 2⋅ ⋅ Cov⁡ ⁡ ()U()k),U()j)){displaystyle operatorname [Var] (U_{(k)}-U_{(j)})=operatorname {Var} (U_{(k)})+operatorname {Var} (U_{(j)})-2cdot operatorname {Cov} (U_{(k)},U_{(j)})={frac {k(n-k+1)}{(n+1)}{2}}}}+{frac {j(n-j+1)}{(n+1)}{2}(n+2)}}-2cdot operatorname {Cov} (U_{(k)},U_{(j)})}

Var⁡ ⁡ ()U)=()k− − j)()n− − ()k− − j)+1)()n+1)2()n+2){displaystyle operatorname {Var} (U)={frac {(k-j)(n-(k-j)+1)}{(n+1)^{2}(n+2)}}} {}} {fn0}} {fn0}}} {fn0}}

U♪ ♪ Beta⁡ ⁡ ()k− − j,n− − ()k− − j)+1){displaystyle Usim operatorname {Beta} (k-j,n-(k-j)+1)}

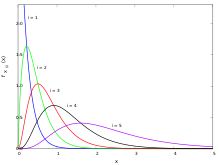
Estadísticas de pedidos muestreadas a partir de una distribución exponencial

Para X1,X2,..,Xn{displaystyle X_{1},X_{2}, X_{n} una muestra al azar del tamaño n de una distribución exponencial con parámetro λ, las estadísticas de pedidos X_()i) para i = 1,2,3,... n cada uno tiene distribución

X()i)=d1λ λ ().. j=1iZjn− − j+1){displaystyle X_{(i)}{stackrel {} {fn} {fnK} {fnh}fnh}}left(sum _{j=1}{i}{i}{frac} {fn} {fn} {fn}} {fn} {fn}} {fn}}}} {fnfn}} {fn}}}}}}}}f}}}}}fnf}fnfnfnfnfn}fnfnfn}}f}fnfn}fn}fnfn}fnfn}fnfnfn}fnfn}fnfn}fnfnfnfnfnfn}fn}fnfn}fn}fnfn}fn}fnfnh}}}}fn {Z_{j}{n-j+1}right)}

donde Z_j son variables aleatorias exponenciales estándar iid (es decir, con parámetro de tasa 1). Este resultado fue publicado por primera vez por Alfréd Rényi.

Estadísticas de pedidos tomadas de una distribución de Erlang

La transformada de Laplace de las estadísticas de pedidos se puede muestrear a partir de una distribución de Erlang a través de un método de conteo de rutas.

La distribución conjunta de las estadísticas de orden de una distribución absolutamente continua

Si F_X es absolutamente continuo, tiene una densidad tal que dFX()x)=fX()x)dx{displaystyle dF_{X}(x)=f_{X}(x),dx}, y podemos utilizar las sustituciones

u=FX()x){displaystyle u=F_{X}(x)}

y

du=fX()x)dx{displaystyle du=f_{X}(x),dx}

para derivar las siguientes funciones de densidad de probabilidad para las estadísticas de orden de una muestra de tamaño n extraída de la distribución de X:

fX()k)()x)=n!()k− − 1)!()n− − k)![FX()x)]k− − 1[1− − FX()x)]n− − kfX()x){displaystyle f_{X_{(k)}}(x)={frac {n}{(k-1)!(n-k)}}}[F_{X}(x)]^{k-1}[1-F_{X}(x)}{n-k}f_{X}(x)}}

fX()j),X()k)()x,Sí.)=n!()j− − 1)!()k− − j− − 1)!()n− − k)![FX()x)]j− − 1[FX()Sí.)− − FX()x)]k− − 1− − j[1− − FX()Sí.)]n− − kfX()x)fX()Sí.){X} {x} {x} {x)} {x_} {x)} {y)} {y)}{j-1)!(k-j-1)! Donde x≤ ≤ Sí.{displaystyle xleq y}

fX()1),...... ,X()n)()x1,...... ,xn)=n!fX()x1)⋯ ⋯ fX()xn){displaystyle f_{X_{(1)},ldotsX_{(n)}(x_{1},ldotsx_{n})=n!f_{X}(x_{1})cdots f_{X}(x_{n})}} Donde x1≤ ≤ x2≤ ≤ ⋯ ⋯ ≤ ≤ xn.{displaystyle x_{1}leq x_{2}leq dots leq x_{n}

Aplicación: intervalos de confianza para cuantiles

Una pregunta interesante es qué tan bien funcionan las estadísticas de orden como estimadores de los cuantiles de la distribución subyacente.

Un ejemplo de tamaño de muestra pequeño

El caso más simple a considerar es qué tan bien la mediana de la muestra estima la mediana de la población.

Como ejemplo, considere una muestra aleatoria de tamaño 6. En ese caso, la mediana de la muestra generalmente se define como el punto medio del intervalo delimitado por las estadísticas de tercer y cuarto orden. Sin embargo, sabemos por la discusión anterior que la probabilidad de que este intervalo realmente contenga la mediana de la población es

()63)()1/2)6=516.. 31% % .{displaystyle {6 choose 3}(1/2)^{6}={5 over 16}approx 31%.}

Aunque la mediana de la muestra probablemente se encuentre entre las mejores estimaciones puntuales independientes de la distribución de la mediana de la población, lo que ilustra este ejemplo es que no es particularmente buena en términos absolutos. En este caso particular, un mejor intervalo de confianza para la mediana es el delimitado por los estadísticos de 2° y 5° orden, que contiene la mediana poblacional con probabilidad

[()62)+()63)+()64)]()1/2)6=2532.. 78% % .{displaystyle left[{6 choose 2}+{6 choose 3}+{6 choose 4}right](1/2)^{6}={25 over 32}approx 78%}

Con un tamaño de muestra tan pequeño, si se quiere al menos un 95 % de confianza, se reduce a decir que la mediana está entre el mínimo y el máximo de las 6 observaciones con probabilidad 31/32 o aproximadamente el 97 %. El tamaño 6 es, de hecho, el tamaño de muestra más pequeño tal que el intervalo determinado por el mínimo y el máximo es al menos un intervalo de confianza del 95% para la mediana de la población.

Muestras grandes

Para la distribución uniforme, como n tiende a infinito, el cuantil de la muestra p^th tiene una distribución normal asintótica, ya que se aproxima por

U()⌈ ⌈ np⌉ ⌉ )♪ ♪ AN()p,p()1− − p)n).{displaystyle U_{(lceil nprceil)}sim ANleft(p,{frac {p(1-p)}{n}right).}

Para una distribución general F con una densidad continua distinta de cero en F ⁻¹(p), se aplica una normalidad asintótica similar:

X()⌈ ⌈ np⌉ ⌉ )♪ ♪ AN()F− − 1()p),p()1− − p)n[f()F− − 1()p))]2){displaystyle X_{(lceil nprceil)}sim ANleft(F^{-1}(p),{frac {p(1-p)}{n[f(F^{-1}(p)]}}}right)}}}

donde f es la función de densidad y F ⁻¹ es la función cuantil asociada con F. Una de las primeras personas en mencionar y probar este resultado fue Frederick Mosteller en su artículo seminal en 1946. Investigaciones posteriores condujeron en la década de 1960 a la representación de Bahadur que proporciona información sobre los límites de error.

Se puede hacer una observación interesante en el caso de que la distribución sea simétrica y la mediana de la población sea igual a la media de la población. En este caso, la media de la muestra, por el teorema del límite central, también se distribuye asintóticamente normalmente, pero con una varianza σ²/n. Este análisis asintótico sugiere que la media supera a la mediana en casos de baja curtosis y viceversa. Por ejemplo, la mediana logra mejores intervalos de confianza para la distribución de Laplace, mientras que la media funciona mejor para X que se distribuyen normalmente.

Prueba

Se puede demostrar que

B()k,n+1− − k)=dXX+Y,{displaystyle B(k,n+1-k) {fncipal {mhm} {}{=}} {frac {X}{X+Y}}}

dónde

X=.. i=1kZi,Y=.. i=k+1n+1Zi,{displaystyle X=sum ¿Qué? Y= ¿Qué?

siendo Z_i variables aleatorias exponenciales independientes idénticamente distribuidas con tasa 1. Dado que X/n y Y/n están asintóticamente distribuidos normalmente por el CLT, nuestros resultados siguen la aplicación del método delta.

Aplicación: Estimación de densidad no paramétrica

Momentos de la distribución para la estadística de primer orden se pueden utilizar para desarrollar un estimador de densidad no paramétrica. Supongamos que queremos estimar la densidad fX{displaystyle F_{X} en el punto xAlternativa Alternativa {displaystyle x^{*}. Considere las variables aleatorias Yi=SilencioXi− − xAlternativa Alternativa Silencio{displaystyle Y..., que son i.i.d con función de distribución gY()Sí.)=fX()Sí.+xAlternativa Alternativa )+fX()xAlternativa Alternativa − − Sí.){displaystyle g_{Y}(y)=f_{X}(y+x^{*})+f_{X}(x^{*}-y) }. En particular, fX()xAlternativa Alternativa )=gY()0)2{displaystyle f_{X}(x^{*}={frac {g_{Y}{2}}}}.

El valor esperado de la estadística de primer orden Y()1){displaystyle Y_{(1)} dada una muestra N{displaystyle N} total observations yields,

E()Y()1))=1()N+1)g()0)+1()N+1)()N+2)∫ ∫ 01Q.()z)δ δ N+1()z)dz[displaystyle E(Y_{(1)})={frac {1}{(N+1)g(0)}+{frac {1}{(N+1)}int _{0}Q'''(z)delta _{N+1}(z),dz}

Donde Q{displaystyle Q} es la función cuantitativa asociada a la distribución gY{displaystyle g_{Y}, y δ δ N()z)=()N+1)()1− − z)N{displaystyle delta _{N}(z)=(N+1)(1-z)^{N}. Esta ecuación en combinación con una técnica de jackknifing se convierte en la base del algoritmo de estimación de densidad siguiente,

 Entrada: Una muestra de     N   {displaystyle N}  observaciones.     {}  x  l l     }  l l  = 1   M     {displaystyle {x_{ell } {fnMicrosoft Sans =1} {M}  puntos de evaluación de densidad. Parámetro de ajuste     a ▪ ▪  () 0 , 1 )   {displaystyle ain (0,1)}  (normalmente 1/3).
Producto:     {}     f ^ ^      l l     }  l l  = 1   M     {displaystyle {hat {f}_{ell} } {fnMicrosoft Sans =1} {M}  densidad estimada en los puntos de evaluación.

 1:      m  N   = redonda ⁡ ⁡  ()  N  1 − −  a   )   {displaystyle m_{N}=operatorname {round} (N^{1-a})} 2:      s  N   =   N  m  N       {displaystyle S_{N}={frac {N}{m_{N}}} 3: Crear un      s  N   × ×   m  N     {displaystyle S_{N}times m_{N}  matriz      M  i j     {displaystyle M_{ij}  que sostiene      m  N     {displaystyle m_{N}  subconjuntos con      s  N     {displaystyle S_{N}  observaciones cada uno.
4: Crear un vector        f ^ ^       {displaystyle {hat {f}}  para mantener las evaluaciones de densidad.
5: para     l l  = 1 → →  M   {displaystyle ell =1to M}  do6: para     k = 1 → →   m  N     {displaystyle k=1to m_{N}  do7: Encuentra la distancia más cercana      d  l l  k     {displaystyle ♪♪  al punto actual      x  l l      {displaystyle x_{ell }  dentro del     k   {displaystyle k} subconjunto
8: final for9: Computar el promedio del subconjunto de distancias a      x  l l    :  d  l l    =  ..   k = 1    m  N        d  l l  k    m  N       {displaystyle x_{ell. }=sum _{k=1} {m_{N}{frac {cHFF} {}{m_{N}}}} {}}} {fn}}}}}} {fn}}}}}}}} {}}}}}} {}}}}}}} {}}}}} {}}}}}}} {}}}}}}} {}}}}}}} {}}}}}}} {}}}}}}}} {}} {}}}}}}}}}}}} {m}}} {m} {m}}}} {m} {m} {}}}} {} {} {}}}}}}}}}}}}}}}}}} {}}}} {} {}}}}}}}}} {} {}}}}}} {} {m}}} {m}}}}}}}}}}}}} {m} {}}}}}}}}}}}}}}}}}}}}}}}}} {}}}}}}}}}}}}}} { 10: Computar la estimación de densidad      x  l l    :     f ^ ^      l l    =   1  2 () 1 +  s  N   )  d  l l         {displaystyle x_{ell]:{hat {f}_{f} }={frac {1}{2(1+s_{N}d_{ell } 11: final for12: retorno        f ^ ^       {displaystyle {hat {f}} 

A diferencia de los parámetros de ajuste basados en ancho de banda/longitud para enfoques basados en histogramas y kernel, el parámetro de ajuste para el estimador de densidad basado en estadísticas de orden es el tamaño de los subconjuntos de muestra. Tal estimador es más robusto que los enfoques basados en histogramas y kernel, por ejemplo, las densidades como la distribución de Cauchy (que carecen de momentos finitos) se pueden inferir sin la necesidad de modificaciones especializadas como los anchos de banda basados en IQR. Esto se debe a que el primer momento de la estadística de orden siempre existe si existe el valor esperado de la distribución subyacente, pero lo contrario no es necesariamente cierto.

Tratar con variables discretas

Suppose X1,X2,...... ,Xn{displaystyle X_{1},X_{2},ldots X_{n} son i.i.d. variables aleatorias de una distribución discreta con función de distribución acumulativa F()x){displaystyle F(x)} y función de masa de probabilidad f()x){displaystyle f(x)}. Para encontrar las probabilidades de kT{displaystyle k^{text{th}}} estadísticas de orden, se necesitan tres valores, a saber:

<math alttext="{displaystyle p_{1}=P(Xx)=1-F(x).}" xmlns="http://www.w3.org/1998/Math/MathML">p1=P()X.x)=F()x)− − f()x),p2=P()X=x)=f()x),yp3=P()X■x)=1− − F()x).{displaystyle p_{1}=P(X=x)=F(x)-f(x), p_{2}=P(X=x)=f(x),{text{ and }}p_{3}=P(X confidencialx)=1-F(x). }<img alt="p_{1}=P(Xx)=1-F(x)." aria-hidden="true" class="mwe-math-fallback-image-inline" src="https://wikimedia.org/api/rest_v1/media/math/render/svg/8ff803d0c5f6c4b8ee7290d65c0d5ef30a8e907b" style="vertical-align: -0.838ex; margin-left: -0.089ex; width:88.882ex; height:2.843ex;"/>

La función de distribución acumulativa de la kT{displaystyle k^{text{th}}} la estadística del orden puede ser calculada notando que

P()X()k)≤ ≤ x)=P()al menoskobservaciones inferiores o iguales ax),=P()hay en la mayorían− − kobservaciones mayoresx),=.. j=0n− − k()nj)p3j()p1+p2)n− − j.{begin{aligned}P(X_{(k)}leq x)}leq=P({text{there are at least }k{ observations less than or equal to }}x),\cl=P({text{there are at most }n-k{text{ observations greater than }{=0}{===0} { choose J}p_{3} {j}(p_{1}+p_{2} {n-j}.end{aligned}}}

Análogamente, <math alttext="{displaystyle P(X_{(k)}P()X()k).x){displaystyle P(X_{(k)}traducidos)}<img alt="P(X_{(k)} es dado por

<math alttext="{displaystyle {begin{aligned}P(X_{(k)}P()X()k).x)=P()al menoskobservaciones menos quex),=P()hay en la mayorían− − kobservaciones mayores o igualesx),=.. j=0n− − k()nj)()p2+p3)j()p1)n− − j.{fnMicrosoft Sans Serif} {fnMicrosoft Sans Serif} {fnMicrosoft Sans Serif} {fn} {fnMicrosoft Sans Serif} {fnMicrosoft Sans Serif} {fnK} {fnMicrosoft Sans Serif} {fnMicrosoft Sans Serif} {f} {f}f}f}f}f}f}fnKf}f}fnMicroscH0}fnKf}fnKf}fnKfnKfnKf}fnKfnKfnKfnKfnKf}fnKfnKfnKfnKfnKfnKfnKfnKfnKfnKfnKfnKfnKfnKf}f}fnMi<img alt="{displaystyle {begin{aligned}P(X_{(k)}

Tenga en cuenta que la función de masa de probabilidad X()k){displaystyle X_{(k)} es sólo la diferencia de estos valores, es decir

<math alttext="{displaystyle {begin{aligned}P(X_{(k)}=x)&=P(X_{(k)}leq x)-P(X_{(k)}P()X()k)=x)=P()X()k)≤ ≤ x)− − P()X()k).x),=.. j=0n− − k()nj)()p3j()p1+p2)n− − j− − ()p2+p3)j()p1)n− − j),=.. j=0n− − k()nj)()()1− − F()x))j()F()x))n− − j− − ()1− − F()x)+f()x))j()F()x)− − f()x))n− − j).{cHFF} {cHFF} {cH00}} {cHFF}} {cHFF} {cH0}}} {cH0}} {cH0} {cH0}} {cH0} {cH00}} {cH0}}}} {cH0} {cH0}}} {cH0}}}}} {cH0}}}}}}} {cH00}}}}}}}}}}} {p}}}}} {cc] {c]<img alt="{begin{aligned}P(X_{(k)}=x)&=P(X_{(k)}leq x)-P(X_{(k)}

Cálculo de estadísticas de pedidos

El problema de calcular el késimo elemento más pequeño (o más grande) de una lista se denomina problema de selección y se resuelve mediante un algoritmo de selección. Aunque este problema es difícil para listas muy grandes, se han creado sofisticados algoritmos de selección que pueden resolver este problema en un tiempo proporcional al número de elementos de la lista, incluso si la lista está totalmente desordenada. Si los datos se almacenan en ciertas estructuras de datos especializadas, este tiempo se puede reducir a O (registro n). En muchas aplicaciones se requieren todas las estadísticas de orden, en cuyo caso se puede usar un algoritmo de ordenación y el tiempo necesario es O(n log n).