Espuma

burbujas de espuma de jabón

Las espumas son materiales formados por bolsas de gas atrapadas en un líquido o sólido.

Una esponja de baño y la cabeza de un vaso de cerveza son ejemplos de espumas. En la mayoría de las espumas, el volumen de gas es grande, con finas películas de líquido o sólido que separan las regiones de gas. Las espumas de jabón también se conocen como suds.

Las espumas sólidas pueden ser de celda cerrada o de celda abierta. En la espuma de celda cerrada, el gas forma bolsas discretas, cada una completamente rodeada por el material sólido. En espuma de celda abierta, las bolsas de gas se conectan entre sí. Una esponja de baño es un ejemplo de espuma de celda abierta: el agua fluye fácilmente a través de toda la estructura, desplazando el aire. Una colchoneta para dormir es un ejemplo de espuma de celda cerrada: las bolsas de gas están selladas entre sí para que la colchoneta no pueda absorber agua.

Las espumas son ejemplos de medios dispersos. En general, el gas está presente, por lo que se divide en burbujas de gas de diferentes tamaños (es decir, el material es polidisperso), separadas por regiones líquidas que pueden formar películas, cada vez más delgadas cuando la fase líquida se drena de las películas del sistema. Cuando la escala principal es pequeña, es decir, para una espuma muy fina, este medio disperso puede considerarse un tipo de coloide.

Espuma también puede referirse a algo que es análogo a la espuma, como la espuma cuántica.

Estructura

Una espuma es, en muchos casos, un sistema multiescala.

Orden y desorden de burbujas en una espuma superficial

Una escala es la burbuja: las espumas de material suelen estar desordenadas y tienen una variedad de tamaños de burbujas. A tamaños mayores, el estudio de espumas idealizadas está íntimamente ligado a los problemas matemáticos de superficies mínimas y teselados tridimensionales, también llamados panales. La estructura de Weaire-Phelan se considera la mejor celda unitaria posible (óptima) de una espuma perfectamente ordenada, mientras que las leyes de Plateau describen cómo las películas de jabón forman estructuras en las espumas.

A una escala más baja que la burbuja está el espesor de la película para espumas metaestables, que puede considerarse una red de películas interconectadas llamadas laminillas. Idealmente, las láminas se conectan en tríadas e irradian 120° hacia afuera desde los puntos de conexión, conocidos como bordes de meseta.

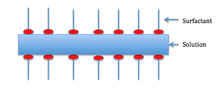
Una escala aún menor es la interfaz líquido-aire en la superficie de la película. La mayoría de las veces esta interfase está estabilizada por una capa de estructura anfifílica, a menudo hecha de surfactantes, partículas (emulsión de Pickering) o asociaciones más complejas.

Propiedades mecánicas de las espumas sólidas

Las espumas sólidas, tanto de celda abierta como de celda cerrada, se consideran una subclase de estructuras celulares. A menudo tienen una conectividad nodal más baja en comparación con otras estructuras celulares como panales y entramados de celosía y, por lo tanto, su mecanismo de falla está dominado por la flexión de los miembros. La baja conectividad nodal y el mecanismo de falla resultante en última instancia conducen a su menor resistencia mecánica y rigidez en comparación con los panales y las celosías de armadura.

La resistencia de las espumas puede verse afectada por la densidad, el material utilizado y la disposición de la estructura celular (abierto frente a cerrado e isotropía de poros). Para caracterizar las propiedades mecánicas de las espumas, se utilizan curvas de tensión-deformación por compresión para medir su resistencia y capacidad para absorber energía, ya que este es un factor importante en las tecnologías basadas en espumas.

Espuma elastomérica

Para los sólidos celulares elastoméricos, a medida que la espuma se comprime, primero se comporta de manera elástica cuando las paredes de las celdas se doblan, luego, cuando las paredes de las celdas se doblan, el material cede y se rompe hasta que finalmente las paredes de las celdas se aplastan y el material se rompe. Esto se ve en una curva de tensión-deformación como un régimen elástico lineal empinado, un régimen lineal con una pendiente poco profunda después de ceder (tensión de meseta) y un régimen que aumenta exponencialmente. La rigidez del material se puede calcular a partir del régimen elástico lineal, donde el módulo para espumas de celdas abiertas se puede definir mediante la ecuación:

Curva de estrés esquemático de una espuma elastómera, demostrando las tres regiones que son elástica lineal, alboroto de pared celular y fractura de pared celular. El área bajo la curva especificada representa la energía por volumen de unidad que la espuma puede absorber.

()EAlternativa Alternativa Es)f=Cf()*** *** Alternativa Alternativa *** *** s)2{displaystyle left({frac {f} {f}f}f} {f}f}f}f}left({frac} {f} {f} {f}} {f}f} {f} {f} {f}}} {f} {f}}f}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}} {p} {p} {p}}p}}}}}}}}}}}}} {p}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}p}}}}}}}}}}p}p}}}}}}}}}}p}p}}p}}}}}p}}}p}p}p}p} {fnMicrosoft Sans Serif}

Donde Es{displaystyle E_{s} es el módulo del componente sólido, EAlternativa Alternativa {displaystyle E^{*} es el módulo de la estructura del panal, Cf{displaystyle C_{f} es una constante teniendo un valor cercano a uno, *** *** Alternativa Alternativa {displaystyle rho ^{*} es la densidad de la estructura del panal, y *** *** s{displaystyle rho _{s}} es la densidad del sólido. El módulo elástico para espumas de células cerradas se puede describir de manera similar por:

()EAlternativa Alternativa Es)f=Cf()*** *** Alternativa Alternativa *** *** s)3{displaystyle left({frac {f} {f}f}f} {f}f}f}f}left({frac} {f} {f} {f}} {f}f} {f} {f} {f}}} {f} {f}}f}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}} {p} {p} {p}}p}}}}}}}}}}}}} {p}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}p}}}}}}}}}}p}p}}}}}}}}}}p}p}}p}}}}}p}}}p}p}p}p} {fnMicrosoft Sans Serif}

donde la única diferencia es el exponente en la dependencia de la densidad. Sin embargo, en materiales reales, una espuma de celda cerrada tiene más material en los bordes de la celda, lo que hace que siga más de cerca la ecuación de las espumas de celda abierta. La relación de la densidad de la estructura de panal en comparación con la estructura sólida tiene un gran impacto en el módulo del material. En general, la resistencia de la espuma aumenta con la densidad de la celda y la rigidez del material de la matriz.

Energía de deformación

Otra propiedad importante que se puede deducir de la curva de tensión-deformación es la energía que la espuma es capaz de absorber. El área bajo la curva (especificada antes de la densificación rápida en la tensión máxima), representa la energía en la espuma en unidades de energía por unidad de volumen. La energía máxima almacenada por la espuma antes de la ruptura se describe mediante la ecuación:

WmaxEs=0,05()*** *** Alternativa Alternativa *** *** s)2[0.975− − 1.4()*** *** Alternativa Alternativa *** *** s)]{displaystyle {frac {W_{max}{E_{s}}=0.05left({frac} {frac} {f} {f}}} {fnK}}} {fnfnh}}}}} {fnfnK}}}}fnKfnKf}}} {f}}}}}}}}}}}}}fnfnfnfnfnfnfnfnKfnKfnKfnKfnKfnKfnKfnKfnKfnKfnKfnKfnKfnKfnKfnKfnKfnKfnKfnKfnKfnKfnKfnKfnKfnKfnKfnKfnKf}fnK {rho ^{}{rho _{s}}right)}left[0.975-1.4left({frac {rho ^{*}{rho _{}}}}right)}}right)}}} {rho}}} {rho}}}}} {rho)}}} {rho}}}}}}}}}}}}}}}}}}}} {h}}}}}}}}} {h}}} {h}}}}}} {h}}}}}}}}}}}}}}}}}}}}}} {h} {h}} {h}}}}}}}}}}}}}}}}}}}}}} {h} {h}} {h} {h}}}}}}} {h}}}}}}}}}}}}}}}}}}}}}}}}}}}}

Esta ecuación se deriva de suponer una espuma idealizada con aproximaciones de ingeniería de resultados experimentales. La mayor parte de la absorción de energía ocurre en la región de estrés de la meseta después del régimen elástico lineal empinado.

Dependencia direccional

La isotropía de la estructura celular y la absorción de fluidos también pueden tener un impacto en las propiedades mecánicas de una espuma. Si hay anisotropía presente, entonces la respuesta de los materiales al estrés dependerá direccionalmente y, por lo tanto, la curva de tensión-deformación, el módulo y la absorción de energía variarán según la dirección de la fuerza aplicada. Además, las estructuras de células abiertas que tienen poros conectados pueden permitir que el agua u otros líquidos fluyan a través de la estructura, lo que también puede afectar la rigidez y las capacidades de absorción de energía.

Formación

Se necesitan varias condiciones para producir espuma: debe haber trabajo mecánico, componentes de superficie activos (tensioactivos) que reducen la tensión superficial y la formación de espuma más rápido que su descomposición. Para crear espuma, se necesita trabajo (W) para aumentar el área de superficie (ΔA):

W=γ γ Δ Δ A{displaystyle W=gamma Delta A,!

donde γ es la tensión superficial.

Una de las formas en que se crea la espuma es a través de la dispersión, donde una gran cantidad de gas se mezcla con un líquido. Un método de dispersión más específico consiste en inyectar un gas a través de un orificio en un sólido en un líquido. Si este proceso se completa muy lentamente, se puede emitir una burbuja desde el orificio a la vez, como se muestra en la imagen a continuación.

A continuación se muestra una de las teorías para determinar el tiempo de separación; sin embargo, mientras que esta teoría produce datos teóricos que coinciden con los datos experimentales, se acepta como mejor explicación el desprendimiento por capilaridad.

La burbuja de aumento del orificio

La fuerza de flotación actúa para elevar la burbuja, que es

Fb=Vg()*** *** 2− − *** *** 1){displaystyle F_{b}=Vg(rho _{2}-rho _{1})!

Donde V{displaystyle V} es el volumen de la burbuja, g{displaystyle g} es la aceleración debido a la gravedad, y ρ₁ es la densidad del gas ρ₂ es la densidad del líquido. La fuerza que trabaja contra la fuerza de flotabilidad es la fuerza de tensión superficial, que es

Fs=2rπ π γ γ {displaystyle F_{s}=2rpi gamma !,

donde γ es la tensión superficial, y r{displaystyle r} es el radio del orificio. A medida que más aire se introduce en la burbuja, la fuerza de flotabilidad crece más rápido que la fuerza de tensión superficial. Así, el desapego ocurre cuando la fuerza de flotabilidad es lo suficientemente grande para superar la fuerza de tensión superficial.

2rpi gamma !}" xmlns="http://www.w3.org/1998/Math/MathML">Vg()*** *** 2− − *** *** 1)■2rπ π γ γ {displaystyle Vg(rho _{2}-rho {1})]Condenado2rpi gamma ! 2r pigamma!" aria-hidden="true" class="mwe-math-fallback-image-inline" src="https://wikimedia.org/api/rest_v1/media/math/render/svg/9ff9ca3a07d2768e0eca0cfacb895cc13dc9ede2" style="vertical-align: -0.838ex; margin-right: -0.387ex; width:19.969ex; height:2.843ex;"/>

Además, si la burbuja es tratada como una esfera con un radio de R{displaystyle R. y el volumen V{displaystyle V} se sustituye a la ecuación anterior, la separación se produce en el momento en que

R3=3rγ γ 2g()*** *** 2− − *** *** 1){displaystyle R^{3}={frac {3rgamma}{2g(rho _{2}-rho ¡No!

Examinar este fenómeno desde un punto de vista capilaridad para una burbuja que se está formando muy lentamente, se puede suponer que la presión p{displaystyle p} dentro es constante en todas partes. La presión hidrostática en el líquido es designada por p0{displaystyle P_{0}. El cambio de presión a través de la interfaz de gas a líquido es igual a la presión capilar; por lo tanto,

p− − p0=γ γ ()1R1+1R2){displaystyle p-p_{0}=gamma left({frac {1} {fn} {fnMicroc}}} {fnMicroc} ¡Sí!

donde R₁ y R₂ son los radios de curvatura y se establecen como positivos. En el tallo de la burbuja, R₃ y R₄ son los radios de curvatura también tratados como positivos. Aquí, la presión hidrostática en el líquido debe tener en cuenta z, la distancia desde la parte superior hasta el tallo de la burbuja. La nueva presión hidrostática en el tallo de la burbuja es p₀(ρ₁ − ρ₂)z. La presión hidrostática equilibra la presión capilar, que se muestra a continuación:

p− − p0− − ()*** *** 2− − *** *** 1)gz=γ γ ()1R3+1R4){displaystyle p-p_{0}-(rho _{2}-rho {})gz=gamma left({frac {1}{3}}+{frac} ¡Sí!

Finalmente, la diferencia en la presión superior e inferior es igual al cambio en la presión hidrostática:

()*** *** 2− − *** *** 1)gz=γ γ ()1R1+1R2− − 1R3− − 1R4){displaystyle (rho _{2}-rho _{1})gz=gamma left({frac} {1} {fn} {fnMicroc}}} {fnMicroc} {1}{2}}-{frac} {1} {R_{3}}-{frac} ¡Sí!

En el tallo de la burbuja, la forma de la burbuja es casi cilíndrica; en consecuencia, R₃ o R₄ es grande mientras que el otro radio de curvatura es pequeño. A medida que el tallo de la burbuja crece en longitud, se vuelve más inestable a medida que uno de los radios crece y el otro se encoge. En cierto punto, la longitud vertical del vástago excede la circunferencia del vástago y, debido a las fuerzas de flotación, la burbuja se separa y el proceso se repite.

Estabilidad

Estabilización

Efecto marangoni de una película

Efecto marangoni de una película (2)

La estabilización de una espuma es provocada por las fuerzas de van der Waals entre las moléculas de la espuma, las dobles capas eléctricas creadas por los tensioactivos dipolares y el efecto Marangoni, que actúa como una fuerza restauradora de las láminas.

El efecto Marangoni depende de que el líquido que está espumando sea impuro. Generalmente, los tensioactivos en la solución disminuyen la tensión superficial. Los tensioactivos también se agrupan en la superficie y forman una capa como se muestra a continuación.

Para que se produzca el efecto Marangoni, la espuma debe tener una muesca como se muestra en la primera imagen. Esta muesca aumenta el área superficial local. Los tensioactivos tienen un tiempo de difusión mayor que la mayor parte de la solución, por lo que los tensioactivos están menos concentrados en la muesca.

Además, el estiramiento de la superficie hace que la tensión superficial del punto dentado sea mayor que la del área circundante. En consecuencia, dado que el tiempo de difusión de los tensioactivos es grande, el efecto Marangoni tiene tiempo para producirse. La diferencia en la tensión superficial crea un gradiente que provoca el flujo de fluido desde las áreas de menor tensión superficial hacia las áreas de mayor tensión superficial. La segunda imagen muestra la película en equilibrio después de que se haya producido el efecto Marangoni.

El curado de una espuma la solidifica, haciéndola indefinidamente estable en STP.

Desestabilización

Witold Rybczynski y Jacques Hadamard desarrollaron una ecuación para calcular la velocidad de las burbujas que suben en espuma con la suposición de que las burbujas son esféricas con un radio r{displaystyle r}.

u=2gr29.. 2()*** *** 2− − *** *** 1)()3.. 1+3.. 23.. 1+2.. 2){displaystyle u={2gr^{2}{9eta _{2}}(rho _{2}-rho _{1})left({frac {3eta _{1}+3eta _{2}}{3eta _{1}+2eta _{2}}}right)}}}}}}displaystyle u={{2} {}{2} {}}}} {}} {}{2}{2}}}} {}}}}}}}}}} {} {}} {} {}{2}{2} {}}}}}}}}}}}}}}}}}}}}}}}}}}}} {}}}}}}}}}}}}}}{2}{2}{2}}}{2}}}} {}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}

con velocidad en unidades de centímetros por segundo. ρ₁ y ρ₂ es la densidad de un gas y un líquido respectivamente en unidades de g/cm³ y ῃ₁ y ῃ₂ es la viscosidad del gas y líquido g/cm·s y g es la aceleración en unidades de cm/s².

Sin embargo, dado que la densidad y la viscosidad de un líquido son mucho mayores que las del gas, se pueden despreciar la densidad y la viscosidad del gas, lo que da como resultado la nueva ecuación para la velocidad de las burbujas que ascienden como:

u=gr23.. 2()*** *** 2){displaystyle u={frac {}{2}{3eta _{2}}(rho _{2})!}

Sin embargo, a través de experimentos se ha demostrado que un modelo más preciso para el aumento de burbujas es:

u=2gr29.. 2()*** *** 2− − *** *** 1){displaystyle u={2gr^{2}{9eta _{2}}(rho _{2}-rho _{1})!}

Las desviaciones se deben al efecto Marangoni y la presión capilar, que afectan la suposición de que las burbujas son esféricas. Para la presión de Laplace de una interfaz gas-líquido curva, los dos radios principales de curvatura en un punto son R₁ y R₂. Con una interfaz curva, la presión en una fase es mayor que la presión en otra fase. La presión capilar P_c viene dada por la ecuación de:

Pc=γ γ ()1R1+1R2){displaystyle P_{c}=gamma left({frac {1} {fn} {fnMicroc}}} {fnMicroc} ¡Sí!,

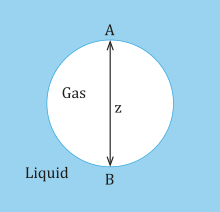
Donde γ γ {displaystyle gamma } es la tensión superficial. La burbuja que se muestra a continuación es un gas (fase 1) en un líquido (fase 2) y punto Un designa la parte superior de la burbuja mientras que el punto B designa la parte inferior de la burbuja.

Bubble for hydrostatic pressure

En la parte superior de la burbuja en el punto A, se supone que la presión en el líquido es p₀ al igual que en el gas. En el fondo de la burbuja en el punto B, la presión hidrostática es:

PB,1=p0+g*** *** 1z{displaystyle P_{B},1=p_{0}+grho ¡No!

PB,2=p0+g*** *** 2z{displaystyle P_{B},2=p_{0}+grho ¡No!

donde ρ₁ y ρ₂ es la densidad de un gas y un líquido respectivamente. La diferencia de presión hidrostática en la parte superior de la burbuja es 0, mientras que la diferencia de presión hidrostática en la parte inferior de la burbuja a través de la interfaz es gz(ρ ₂ − ρ₁). Suponiendo que los radios de curvatura en el punto A son iguales y se denotan por R_A y que los radios de curvatura en el punto B son iguales y se denotan por R_B, entonces la diferencia en la presión capilar entre el punto A y el punto B es:

Pc=2γ γ ()1RA− − 1RB){displaystyle P_{c}=2gamma left({frac {1} {R_{A}}-{frac} ¡Sí!

En el equilibrio, la diferencia de presión capilar debe equilibrarse con la diferencia de presión hidrostática. Por eso,

gz()*** *** 2− − *** *** 1)=2γ γ ()1RA− − 1RB){displaystyle gz(rho _{2}-rho #2gamma left # {1} {R_{A}}-{frac} ¡Sí!

Dado que la densidad del gas es menor que la densidad del líquido, el lado izquierdo de la ecuación siempre es positivo. Por lo tanto, el inverso de R_A debe ser mayor que el de R_B. Lo que significa que desde la parte superior de la burbuja hasta la parte inferior de la burbuja, el radio de curvatura aumenta. Por tanto, sin descuidar la gravedad las burbujas no pueden ser esféricas. Además, a medida que z aumenta, esto provoca la diferencia en R_A y R_B también, lo que significa que la burbuja se desvía más de su forma cuanto más crece.

La desestabilización de la espuma ocurre por varias razones. Primero, la gravitación provoca el drenaje de líquido a la base de espuma, que Rybczynski y Hadamar incluyen en su teoría; sin embargo, la espuma también se desestabiliza debido a que la presión osmótica provoca el drenaje de las laminillas a los bordes de la meseta debido a las diferencias de concentración interna en la espuma, y la presión de Laplace provoca la difusión de gas de burbujas pequeñas a grandes debido a la diferencia de presión. Además, las películas pueden romperse bajo la presión de desunión. Estos efectos pueden conducir a la reorganización de la estructura de la espuma a escalas mayores que las burbujas, que pueden ser individuales (proceso T1) o colectivas (incluso del tipo "avalancha").

Experimentos y caracterizaciones

Al ser un sistema multiescala que involucra muchos fenómenos y un medio versátil, la espuma se puede estudiar usando muchas técnicas diferentes. Teniendo en cuenta las diferentes escalas, las técnicas experimentales son las de difracción, principalmente técnicas de dispersión de luz (DWS, véase más abajo, dispersión de luz estática y dinámica, dispersión de rayos X y neutrones) a escalas submicrométricas, o microscópicas. Considerando el sistema como continuo, sus propiedades a granel se pueden caracterizar por la transmitancia de la luz pero también por la conductimetría. La correlación entre estructura y volumen se evidencia con mayor precisión en la acústica en particular. La organización entre burbujas se ha estudiado numéricamente utilizando intentos secuenciales de evolución de la energía superficial mínima de forma aleatoria (modelo de Pott) o determinista (evolucionador de superficie). La evolución con el tiempo (es decir, la dinámica) se puede simular usando estos modelos, o el modelo de burbujas (Durian), que considera el movimiento de burbujas individuales.

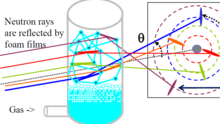
Se pueden realizar observaciones de la estructura a pequeña escala iluminando la espuma con luz láser o haces de rayos X y midiendo la reflectividad de las películas entre las burbujas. Las observaciones de la estructura global se pueden realizar mediante la dispersión de neutrones.

Reflexión de la radiación por una espuma

Principio de medición de dispersión de luz múltiple junto con escaneo vertical

Una técnica óptica típica de dispersión (o difusión) de luz, la dispersión de luz múltiple junto con el escaneo vertical, es la técnica más utilizada para monitorear el estado de dispersión de un producto, identificando y cuantificando así los fenómenos de desestabilización. Funciona en cualquier dispersión concentrada sin dilución, incluidas las espumas. Cuando se envía luz a través de la muestra, las burbujas la retrodispersan. La intensidad de la retrodispersión es directamente proporcional al tamaño y la fracción de volumen de la fase dispersa. Por lo tanto, se detectan y controlan los cambios locales de concentración (drenaje, sinéresis) y los cambios globales de tamaño (maduración, coalescencia).

Aplicaciones

Espumas líquidas

Las espumas líquidas se pueden utilizar en espumas ignífugas, como las que se utilizan para extinguir incendios, especialmente los de petróleo.

De alguna manera, el pan con levadura es una espuma, ya que la levadura hace que el pan suba produciendo pequeñas burbujas de gas en la masa. La masa se ha entendido tradicionalmente como una espuma de celda cerrada, en la que los poros no se conectan entre sí. Cortar la masa libera el gas de las burbujas que se cortan, pero el gas del resto de la masa no puede escapar. Cuando se permite que la masa suba demasiado, se convierte en una espuma de celda abierta, en la que se conectan las bolsas de gas. Cortar la masa o romper la superficie en ese punto provocaría que escapara un gran volumen de gas y la masa colapsaría. La estructura abierta de una masa sobrelevada es fácil de observar: en lugar de consistir en burbujas de gas discretas, la masa consiste en un espacio de gas lleno de hilos de la pasta de harina y agua. Investigaciones recientes han indicado que la estructura de los poros del pan está interconectada en un 99 % en una gran vacuola, por lo que la espuma de celda cerrada de la masa húmeda se transforma en una espuma sólida de celda abierta en el pan.

La propiedad única de las espumas gas-líquido que tienen un área de superficie específica muy alta se aprovecha en los procesos químicos de flotación y fraccionamiento de espuma.

Espumas sólidas

Las espumas sólidas son una clase de materiales ligeros de ingeniería celular. Estas espumas se clasifican típicamente en dos tipos según su estructura de poros: espumas estructuradas de celdas abiertas (también conocidas como espumas reticuladas) y espumas de celdas cerradas. Con resoluciones de celda lo suficientemente altas, cualquier tipo puede tratarse como continuo o "continuo" materiales y se conocen como sólidos celulares, con propiedades mecánicas predecibles.

Las espumas de celda abierta se pueden usar para filtrar el aire. Por ejemplo, se ha demostrado que una espuma incrustada con catalizador convierte catalíticamente el formaldehído en sustancias benignas cuando el aire contaminado con formaldehído pasa a través de la estructura de celda abierta.

Las espumas con estructura de celdas abiertas contienen poros que están conectados entre sí y forman una red interconectada que es relativamente blanda. Las espumas de celda abierta se llenan con cualquier gas que las rodee. Si se llena con aire, se obtiene un aislante relativamente bueno, pero si las celdas abiertas se llenan de agua, se reducirían las propiedades de aislamiento. Estudios recientes se han centrado en estudiar las propiedades de las espumas de celda abierta como material aislante. Se han producido bioespumas de gluten de trigo/TEOS, que muestran propiedades aislantes similares a las espumas obtenidas a partir de recursos derivados del petróleo. La gomaespuma es un tipo de espuma de celda abierta.

Las espumas de celda cerrada no tienen poros interconectados. Las espumas de celda cerrada normalmente tienen una mayor resistencia a la compresión debido a sus estructuras. Sin embargo, las espumas de celda cerrada también son, en general, más densas, requieren más material y, como consecuencia, son más caras de producir. Las celdas cerradas se pueden llenar con un gas especializado para proporcionar un mejor aislamiento. Las espumas de estructura de celda cerrada tienen mayor estabilidad dimensional, bajos coeficientes de absorción de humedad y mayor resistencia en comparación con las espumas de estructura de celda abierta. Todos los tipos de espuma se utilizan ampliamente como material de núcleo en materiales compuestos estructurados en sándwich.

El primer uso de ingeniería conocido de sólidos celulares es con madera, que en su forma seca es una espuma de celda cerrada compuesta de lignina, celulosa y aire. Desde principios del siglo XX, se empezaron a utilizar varios tipos de espumas sólidas especialmente fabricadas. La baja densidad de estas espumas las hace excelentes como aislantes térmicos y dispositivos de flotación y su ligereza y compresibilidad las hacen ideales como materiales de empaque y rellenos.

Un ejemplo del uso de azodicarbonamida como agente de expansión se encuentra en la fabricación de espumas de vinilo (PVC) y EVA-PE, donde desempeña un papel en la formación de burbujas de aire al descomponerse en gas a alta temperatura.

El azar o "estocástico" la geometría de estas espumas también las hace buenas para la absorción de energía. Desde finales del siglo XX hasta principios del siglo XXI, las nuevas técnicas de fabricación han permitido una geometría que da como resultado una excelente resistencia y rigidez por peso. Estos nuevos materiales se denominan típicamente sólidos celulares de ingeniería.

Espuma sintáctica

Una clase especial de espumas de celda cerrada, conocida como espuma sintáctica, contiene partículas huecas incrustadas en un material matriz. Las esferas pueden estar hechas de varios materiales, incluidos vidrio, cerámica y polímeros. La ventaja de las espumas sintácticas es que tienen una relación resistencia-peso muy alta, lo que las convierte en materiales ideales para muchas aplicaciones, incluidas las aplicaciones espaciales y de aguas profundas. Una espuma sintáctica particular emplea un polímero con memoria de forma como su matriz, lo que permite que la espuma adquiera las características de las resinas con memoria de forma y los materiales compuestos; es decir, tiene la capacidad de remodelarse repetidamente cuando se calienta por encima de cierta temperatura y se enfría. Las espumas con memoria de forma tienen muchas aplicaciones posibles, como soporte estructural dinámico, núcleo de espuma flexible y relleno de espuma expandible.

Espuma integral para la piel

Espuma de piel integral, también conocida como espuma de piel propia, es un tipo de espuma con una piel de alta densidad y un núcleo de baja densidad. Puede formarse en un proceso de molde abierto o un proceso de molde cerrado. En el proceso de molde abierto, se mezclan dos componentes reactivos y se vierten en un molde abierto. Luego se cierra el molde y se deja que la mezcla se expanda y cure. Ejemplos de artículos producidos mediante este proceso incluyen reposabrazos, asientos para bebés, suelas de zapatos y colchones. El proceso de molde cerrado, más comúnmente conocido como moldeo por inyección de reacción (RIM), inyecta los componentes mezclados en un molde cerrado bajo altas presiones.

Desespumante

La espuma, que en este caso significa "líquido burbujeante", también se produce como un subproducto no deseado en la fabricación de diversas sustancias. Por ejemplo, la espuma es un problema serio en la industria química, especialmente para procesos bioquímicos. Muchas sustancias biológicas, por ejemplo proteínas, crean fácilmente espuma con agitación o aireación. La espuma es un problema porque altera el flujo de líquido y bloquea la transferencia de oxígeno del aire (previniendo así la respiración microbiana en los procesos de fermentación aeróbica). Por este motivo, se añaden agentes antiespumantes, como los aceites de silicona, para prevenir estos problemas. Los métodos químicos de control de la espuma no siempre son deseables con respecto a los problemas (es decir, contaminación, reducción de la transferencia de masa) que pueden causar, especialmente en las industrias alimentaria y farmacéutica, donde la calidad del producto es de gran importancia. Los métodos mecánicos para prevenir la formación de espuma son más comunes que los químicos.

Velocidad del sonido

La propiedad acústica de la velocidad del sonido a través de una espuma es de interés cuando se analizan fallas de componentes hidráulicos. El análisis implica calcular los ciclos hidráulicos totales hasta la falla por fatiga. La velocidad del sonido en una espuma está determinada por las propiedades mecánicas del gas que crea la espuma: oxígeno, nitrógeno o combinaciones.

Asumir que la velocidad del sonido se basa en las propiedades del fluido del líquido genera errores en el cálculo de los ciclos de fatiga y fallas en los componentes hidráulicos mecánicos. El uso de transductores acústicos e instrumentación relacionada que establecen límites bajos (0 - 50 000 Hz con atenuación) provoca errores. La baja caída durante la medición de la frecuencia real de los ciclos acústicos da como resultado un error de cálculo debido a los ciclos hidráulicos reales en los rangos posibles de 1 a 1000 MHz o más. Los sistemas de instrumentación son más reveladores cuando los anchos de banda de los ciclos exceden los ciclos reales medidos por un factor de 10 a 100. Los costos de instrumentación asociados también aumentan por factores de 10 a 100.

La mayoría de los componentes hidromecánicos en movimiento ciclan entre 0 y 50 Hz, pero las burbujas de gas arrastradas que generan una condición espumosa en el fluido hidráulico asociado generan ciclos hidráulicos reales que pueden superar los 1000 MHz incluso si los componentes mecánicos en movimiento no ciclan a la mayor frecuencia de ciclo.

Galería

• 

  Cierre de la espuma marina (plancton descomposición) en una piscina de marea

• 

  Aluminio espumado

• 

  Micrografía de espuma templada (memoria)

• 

  Sello de penetración de espuma de silicona

• 

  Diet Coca y Mentos espuma "geyser"

• 

  Escaneo industrial de una bola de espuma

• 

  Cojín de espuma de poliestireno

Escamas y propiedades de la espuma