Espirógrafo

El Spirograph es un dispositivo de dibujo geométrico que produce curvas de ruleta matemática de la variedad técnicamente conocida como hipotrocoides y epitrocoides. La conocida versión de juguete fue desarrollada por el ingeniero británico Denys Fisher y vendida por primera vez en 1965.

El nombre es una marca registrada de Hasbro Inc. desde 1998 tras la compra de la empresa que había adquirido la empresa Denys Fisher. La marca Spirograph fue relanzada a nivel mundial en 2013, con sus configuraciones de producto originales, por Kahootz Toys.

Historia

En 1827, el arquitecto e ingeniero inglés nacido en Grecia Peter Hubert Desvignes desarrolló y anunció un "Speiragraph", un dispositivo para crear elaborados dibujos en espiral. Un hombre llamado J. Jopling pronto afirmó haber inventado métodos similares. Mientras trabajaba en Viena entre 1845 y 1848, Desvignes construyó una versión de la máquina que ayudaría a prevenir las falsificaciones de billetes, ya que cualquiera de las variaciones casi infinitas de patrones de ruleta que podía producir era extremadamente difícil de aplicar ingeniería inversa. El matemático Bruno Abakanowicz inventó un nuevo espirógrafo entre 1881 y 1900. Sirvió para calcular un área delimitada por curvas.

Los juguetes para dibujar basados en engranajes existen desde al menos 1908, cuando se anunciaba The Marvelous Wondergraph en el catálogo de Sears. En 1913 apareció un artículo que describía cómo hacer una máquina de dibujo Wondergraph en la publicación Boys Mechanic.

El juguete Spirograph definitivo fue desarrollado por el ingeniero británico Denys Fisher entre 1962 y 1964 creando máquinas de dibujo con piezas de Meccano. Fisher exhibió su espirógrafo en la Feria Internacional del Juguete de Nuremberg de 1965. Posteriormente fue producido por su empresa. Los derechos de distribución en Estados Unidos fueron adquiridos por Kenner, Inc., que lo introdujo en el mercado estadounidense en 1966 y lo promocionó como un juguete creativo para niños. Más tarde, Kenner presentó Spirotot, Magnetic Spirograph, Spiroman y varios juegos de recarga.

En 2013, Kahootz Toys relanzó la marca Spirograph en todo el mundo, con los engranajes y ruedas originales. Los productos modernos utilizan masilla removible en lugar de pasadores para mantener las piezas estacionarias en su lugar. El Spirograph fue Juguete del Año en 1967 y finalista de Juguete del Año, en dos categorías, en 2014. Kahootz Toys fue adquirida por PlayMonster LLC en 2019.

Operación

El Spirograph original lanzado en Estados Unidos constaba de dos anillos de plástico (o estatores) de diferentes tamaños, con dientes de engranaje tanto en el interior como en el exterior de sus circunferencias. Una vez que cualquiera de estos anillos se mantuvo en su lugar (ya sea con alfileres, con un adhesivo o con la mano), cualquiera de las varias ruedas dentadas (o rotores) proporcionadas, cada una con orificios para un bolígrafo, se podía girar alrededor del anillo para dibujar formas geométricas. . Más tarde, el Super-Spirograph introdujo formas adicionales como anillos, triángulos y barras rectas. Todos los bordes de cada pieza tienen dientes para enganchar cualquier otra pieza; Los engranajes más pequeños caben dentro de los anillos más grandes, pero también pueden girar a lo largo de los anillos. borde exterior o incluso uno alrededor del otro. Los engranajes se pueden combinar en muchas disposiciones diferentes. Los juegos a menudo incluían bolígrafos de varios colores, que podían mejorar un diseño cambiando de color, como se ve en los ejemplos que se muestran aquí.

Los principiantes a menudo deslizan los engranajes, especialmente cuando usan los orificios cerca del borde de las ruedas más grandes, lo que resulta en líneas quebradas o irregulares. Los usuarios experimentados pueden aprender a mover varias piezas entre sí (por ejemplo, el triángulo alrededor del anillo, con un círculo "trepando" desde el anillo hasta el triángulo).

• 
  Animación de un espirógrafo
• 
  Varios diseños de espirógrafo dibujados con un conjunto de espirógrafos utilizando varios plumas de diferentes colores
• 
  Cierre de una rueda de espirógrafo

Base matemática

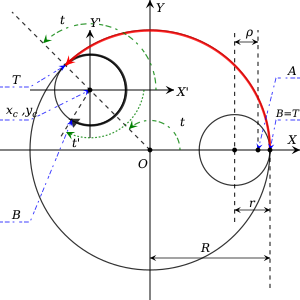
Considerar un círculo exterior fijo ${\displaystyle C.$ de radio ${\displaystyle R.$ centrado en el origen. Un círculo interior más pequeño ${\displaystyle C_{i}$ de radio ${\displaystyle rcanta}$ está rodando dentro ${\displaystyle C.$ y es continuamente tangente a ella. ${\displaystyle C_{i}$ se supone que nunca se deslizan ${\displaystyle C.$ (en un verdadero Spirograph, los dientes en ambos círculos evitan tal deslizamiento). Ahora asume que un punto ${\displaystyle A}$ tumbado en algún lugar ${\displaystyle C_{i}$ se encuentra a distancia ${\displaystyle \rho]$ desde ${\displaystyle C_{i}$Es el centro. Este punto ${\displaystyle A}$ corresponde al agujero de la pluma en el disco interior de un verdadero Spirograph. Sin pérdida de generalidad se puede asumir que en el momento inicial el punto ${\displaystyle A}$ estaba en ${\displaystyle X}$ Axis. Para encontrar la trayectoria creada por un Spirograph, siga el punto ${\displaystyle A}$ como el círculo interno está en movimiento.

Ahora marque dos puntos ${\displaystyle T}$ on ${\displaystyle C.$ y ${\displaystyle B}$ on ${\displaystyle C_{i}$. El punto ${\displaystyle T}$ siempre indica la ubicación donde los dos círculos son tangentes. Punto ${\displaystyle B}$, sin embargo, seguirá ${\displaystyle C_{i}$, y su ubicación inicial coincide con ${\displaystyle T}$. Después de establecer ${\displaystyle C_{i}$ en movimiento en sentido contrario alrededor ${\displaystyle C.$, ${\displaystyle C_{i}$ tiene una rotación de reloj con respecto a su centro. La distancia que apunta ${\displaystyle B}$ cruces en ${\displaystyle C_{i}$ es igual que el que atraviesa el punto tangente ${\displaystyle T}$ on ${\displaystyle C.$, debido a la ausencia de deslizamiento.

Ahora defina el nuevo sistema (relativo) de coordenadas ${\displaystyle (X',Y')}$ con su origen en el centro de ${\displaystyle C_{i}$ y sus ejes paralelos ${\displaystyle X}$ y ${\displaystyle Sí.$. Dejar el parámetro ${\displaystyle t}$ ser el ángulo por el cual el punto tangente ${\displaystyle T}$ giratorios en ${\displaystyle C.$, y ${\displaystyle t}$ ser el ángulo por el cual ${\displaystyle C_{i}$ rota (es decir, por la cual ${\displaystyle B}$ viajes) en el sistema relativo de coordenadas. Porque no hay deslizamiento, las distancias viajadas por ${\displaystyle B}$ y ${\displaystyle T}$ a lo largo de sus respectivos círculos debe ser el mismo, por lo tanto

${\displaystyle tR=(t-t')r,}$

o equivalentemente,

${\displaystyle No.$

Es común suponer que un movimiento en sentido contrario corresponde a un cambio positivo de ángulo y un giro en sentido de reloj a un cambio negativo de ángulo. Un signo menos en la fórmula anterior (${\displaystyle t'traducido0}$) acomoda esta convención.

Vamos. ${\displaystyle (x_{c},y_{c}}$ ser las coordenadas del centro de ${\displaystyle C_{i}$ en el sistema absoluto de coordenadas. Entonces... ${\displaystyle R-r.$ representa el radio de la trayectoria del centro de ${\displaystyle C_{i}$, que (de nuevo en el sistema absoluto) experimenta movimiento circular por lo tanto:

${\displaystyle {\begin{aligned}x_{c} limit=(R-r)\cos t,\y_{c} {=(R-r)\sin t.\end{aligned}}}$

Como se ha definido anteriormente, ${\displaystyle t}$ es el ángulo de rotación en el nuevo sistema relativo. Porque punto ${\displaystyle A}$ obedece la ley habitual de movimiento circular, sus coordenadas en el nuevo sistema relativo de coordenadas ${\displaystyle (x',y')}$ son

${\displaystyle {\begin{aligned}x' limit=\rho \cos t',\\y'corpora=\rho \sin t'.\end{aligned}}}$

Para obtener la trayectoria de ${\displaystyle A}$ en el sistema absoluto (antiguo) de coordenadas, añadir estos dos movimientos:

${\displaystyle {\begin{aligned}x limit=x_{c}+x'=(R-r)\cos t+\rho \cos t',\\\\y Pulse=y_{c}+y'= ¿Qué?$

Donde ${\displaystyle \rho }$ se define arriba.

Ahora, utilice la relación entre ${\displaystyle t}$ y ${\displaystyle t}$ como derivado arriba para obtener ecuaciones que describen la trayectoria de punto ${\displaystyle A}$ en términos de un solo parámetro ${\displaystyle t}$:

${\displaystyle {\begin{aligned}x=x_{c}+x'=(R-r)\cos t+\rho \cos {\frac} {R-R} {R} {r} t,\\\\\\\\c}\\\cH00\cHFF}t,\\\\\\\\\\\\\\\\\\\\\\\cH00\cH00\cH00\\\cH00\cH00\cH00\cH00\cH00\cH00\cH00\\\cH00\cH00\cH00\cH00\cH00\cH00\cH00\cH00\cH00\cH00\cH00\cH00\cH00\cH00\cH00\cH00\cH00\cH00\cH00\cH00\\cH00\cH00\\cH00\cH00\cH00\cH00\cH00\cH00\\cH00\cH00\cH00\cH00\cH00\cHFFFF}\cH00\cH00\cH00\ R-r)\sin t-\rho \sin {\frac {R-R} {R} {R-R} {R-R} {R-R} {R} {R} {R} {R-R} {R} {R-r} {} {} {} {} {} {R-r} {} {} {} {} {} {} {} {} {} {\\\\\\\\\\\fn}}}}}}}}}}}}}}}} {\\\\\f}}}}}}} {\\\\\\\\\\\\\\\\f}}}}}}}}}}}}}}}}} {\\\\\\\\\\\\\\\\f}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}} {\\\$

(utilizando el hecho de que esa función ${\displaystyle \sin }$ es extraño).

Es conveniente representar la ecuación anterior en términos del radio ${\displaystyle R.$ de ${\displaystyle C.$ y sin dimensión parámetros que describen la estructura del Spirograph. Es decir, deja

${\displaystyle l={\frac {\f} {\f}} {\f}} {\f}}} {\f}} {\f}} {\f}}}$

y

${\displaystyle k={\frac {R}}$

El parámetro ${\displaystyle 0\leq l\leq 1}$ representa hasta qué punto ${\displaystyle A}$ se encuentra desde el centro de ${\displaystyle C_{i}$. Al mismo tiempo, ${\displaystyle 0\leq k\leq 1}$ representa lo grande que el círculo interior ${\displaystyle C_{i}$ con respecto al exterior ${\displaystyle C.$.

Ahora se observa que

${\displaystyle {\frac {\fnMicroc} } {R}=lk,}$

y por lo tanto las ecuaciones de trayectoria toman la forma

${\displaystyle {\begin{aligned}x(t) limit=R\left[(1-k)\cos t+lk\cos {\frac {1-k}{k}}}t\right],\y(t) limit=R\left[(1-k)\sin t-lk\lksin {\frac] {1-k}{k}t\right].$

Parámetro ${\displaystyle R.$ es un parámetro de escalado y no afecta la estructura del Spirograph. Diferentes valores de ${\displaystyle R.$ produciría dibujos similares de Spirograph.

Los dos casos extremos ${\displaystyle k=0}$ y ${\displaystyle k=1}$ resultado en trayectorias degeneradas del Spirograph. En el primer caso extremo, cuando ${\displaystyle k=0}$, tenemos un círculo simple de radio ${\displaystyle R.$, correspondiente al caso donde ${\displaystyle C_{i}$ ha sido arrugado en un punto. (División por ${\displaystyle k=0}$ en la fórmula no es un problema, ya que ambos ${\displaystyle \sin }$ y ${\displaystyle \cos }$ son funciones limitadas.)

El otro caso extremo ${\displaystyle k=1}$ corresponde al círculo interior ${\displaystyle C_{i}$Es radio ${\displaystyle r}$ emparejando el radio ${\displaystyle R.$ del círculo exterior ${\displaystyle C.$, es decir. ${\displaystyle r=R}$. En este caso la trayectoria es un solo punto. Intuitivamente, ${\displaystyle C_{i}$ es demasiado grande para rodar dentro del mismo tamaño ${\displaystyle C.$ sin deslizarse.

Si ${\displaystyle l=1}$, entonces el punto ${\displaystyle A}$ está en la circunferencia ${\displaystyle C_{i}$. En este caso las trayectorias se llaman hipocicloides y las ecuaciones anteriores reducen a las de una hipocicloides.