Espiral de Fermat

La espiral de Fermat: un título0, una rama

r=+aφ φ {displaystyle r=+a{sqrt {varphi }

La espiral de Fermat, ambas ramas

Una espiral de Fermat o espiral parabólica es una curva plana con la propiedad de que el área entre dos vueltas completas consecutivas alrededor de la espiral es invariable. Como resultado, la distancia entre vueltas crece en proporción inversa a su distancia desde el centro de la espiral, en contraste con la espiral de Arquímedes (para la cual esta distancia es invariable) y la espiral logarítmica (para la cual la distancia entre vueltas es proporcional a la distancia desde el centro). Las espirales de Fermat llevan el nombre de Pierre de Fermat.

Sus aplicaciones incluyen la combinación continua de curvaturas de curvas, el modelado del crecimiento de plantas y las formas de ciertas galaxias espirales, y el diseño de condensadores variables, conjuntos de reflectores de energía solar y ciclotrones.

Representación coordinada

Polares

La representación de la espiral Fermat en coordenadas polares ()r,φ φ ){displaystyle (r,varphi)} es dado por la ecuación

r=± ± aφ φ {displaystyle r=pm a{sqrt {varphi }

φ φ ≥ ≥ 0{displaystyle varphi geq 0}

Las dos opciones de signo dan las dos ramas de la espiral, que se encuentran suavemente en el origen. Si las mismas variables se reinterpretaran como coordenadas cartesianas, esta sería la ecuación de una parábola con eje horizontal, que nuevamente tiene dos ramas arriba y abajo del eje, que se encuentran en el origen.

Cartesiana

La espiral Fermat con ecuación polar r=± ± aφ φ {displaystyle r=pm a{sqrt {varphi } se puede convertir en las coordenadas cartesianas ()x,Sí.){displaystyle (x,y)} utilizando las fórmulas de conversión estándar x=r#⁡ ⁡ φ φ {displaystyle x=rcos varphi } y Sí.=rpecado⁡ ⁡ φ φ {displaystyle y=rsin varphi }. Usando la ecuación polar para la espiral para eliminar r{displaystyle r} de estas conversiones produce ecuaciones paramétricas para una rama de la curva:

{}x()φ φ )=+aφ φ #⁡ ⁡ ()φ φ )Sí.()φ φ )=+aφ φ pecado⁡ ⁡ ()φ φ ){displaystyle {begin{cases}x(varphi)=+a{sqrt {varphi }cos(varphi)y(varphi)=+a{sqrt {varphi }sin(varphi)end{cases}}}}}}}

y el segundo

{}x()φ φ )=− − aφ φ #⁡ ⁡ ()φ φ )Sí.()φ φ )=− − aφ φ pecado⁡ ⁡ ()φ φ ){displaystyle {begin{cases}x(varphi)=-a{sqrt {varphi }cos(varphi)y(varphi)=-a{sqrt {varphi }sin(varphi)end{cases}}}}}}}

Generan los puntos de las ramas de la curva como parámetro φ φ {displaystyle varphi } abarca los números reales positivos.

Para cualquier ()x,Sí.){displaystyle (x,y)} generada de esta manera, dividiendo x{displaystyle x} por Sí.{displaystyle y} cancela el aφ φ {textstyle a{sqrt {varphi } partes de las ecuaciones paramétricas, dejando la ecuación más simple xSí.=cot⁡ ⁡ ()φ φ ){displaystyle {tfrac {x}{y}=cot left(varphi right)}. De esta ecuación, sustitución φ φ {displaystyle varphi } por φ φ =r2/a2{textstyle varphi =r^{2}/a^{2} (una forma reorganizada de la ecuación polar para la espiral) y luego sustitución r{displaystyle r} por r=x2+Sí.2{textstyle r={sqrt {x^{2}+y^{2}}} (la conversión de Cartesian a polar) deja una ecuación para la espiral Fermat en términos sólo x{displaystyle x} y Sí.{displaystyle y}:

xSí.=cot⁡ ⁡ ()x2+Sí.2a2).{displaystyle {frac {x}{y}=cot left({frac ¿Qué?

a{displaystyle a}

Propiedades geométricas

La espiral de un Fermat divide el plano en dos regiones conectadas (diagrama: blanco y negro)

División del avión

Una espiral de Fermat completa (ambas ramas) es una suave curva libre de dos puntos, en contraste con la espiral hiperbólica y de Arquímedes. Como una línea, un círculo o una parábola, divide el plano en dos regiones conectadas.

Definición de sector (azul claro) y ángulo de pendiente polar α

Pendiente polar

A partir del cálculo vectorial en coordenadas polares se obtiene la fórmula

#⁡ ⁡ α α =r.r{displaystyle tan alpha ={frac {r} {r}}

para la pendiente polar y su ángulo α entre la tangente de una curva y la correspondiente círculo polar (ver diagrama).

Para la espiral de Fermat r = a√φ se obtiene

#⁡ ⁡ α α =12φ φ .{displaystyle tan alpha = {frac {1}{2varphi }}

Por lo tanto, el ángulo de la pendiente disminuye monótonamente.

Curvatura

De la fórmula

κ κ =r2+2()r.)2− − rr.()r2+()r.)2)32{displaystyle kappa ={2}+2(r')^{2}-r,r'}{left(r^{2}+(r')^{2}right)^{2}frac {3}{2}}}} {}}} {}}}}} {}}}} {}}}} {}}}} {}}}} {}}}}} {}}}}} {}}}} {}}}} {}}}}}}} {}}}}}}} {}}}}} {}}}}}}} {}}}}}}} {}}}}}}}}}}}}}}} {}}}}}}}}}}}}}}}}}} {}}}}}}}}}}}}} {}}}}}}}}}}}}}}}}}}}}}}}}}}}} {}}}}}}}}}}}}}}}}}}}}}}}}} {}}}}}}}}}}}}}}}}}}}} {}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}

para la curvatura de una curva con ecuación polar r = r(φ) y sus derivados

r.=a2φ φ =a22rr.=− − a4φ φ 3=− − a44r3{displaystyle {begin{aligned}r' limit={tfrac {a}{2{sqrt {varphi} }={tfrac {cHFF} {cH00}\cH00}\cH00} {cHFF} {cH00}}\cH00}cH00} {cHFF} {cH00}} {cH00}}}\cH00}\cH00}\cH00}\cH00}}\\\\cH00}}}\\\\\cH00}\\cH00}cH00cH00cH00cH00}\cH00}\cH00}}\\\\\\\cH00}}\\\\cH00}\cH00}\\\\\cH00}\cH00}\cH00}}\\\\\\\cH00}}}\cH }{3}=-{tfrac {fn} {fn}} {fnK}} {fn}}} {fnK}}}} {fn}}} {fn}}}}}}} {fn}}} {fn}}}}}}}}} {f}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}} {end {pend} {pend} {pend} {f} {f} {f} {f} {f} {f} {f} {f} {f} {f} {f} {f} {f} {f} {f} {f} {f}} {f} {f} {f} {f} {f} {f} {f}}} {f}}}}}}}}}}}}}}}}}}}

se obtiene la curvatura de una espiral de Fermat:

κ κ ()r)=2r()4r4+3a4)()4r4+a4)32.{displaystyle kappa (r)={frac {2rleft(4r^{4}+3a^{4}right)}{left(4r^{4}+a^{4}right)^{frac] {3} {2}}}}}}

En el origen, la curvatura es 0. Por lo tanto, la curva completa tiene en el origen un punto de inflexión y el eje x es su tangente allí.

Área entre arcos

El área de un sector de la espiral de Fermat entre dos puntos (r(φ₁), φ₁) y (r (φ₂), φ₂) es

A¿Qué? ¿Qué? =12∫ ∫ φ φ 1φ φ 2r()φ φ )2dφ φ =12∫ ∫ φ φ 1φ φ 2a2φ φ dφ φ =a24()φ φ 22− − φ φ 12)=a24()φ φ 2+φ φ 1)()φ φ 2− − φ φ 1).{displaystyle {begin{aligned}{compline {fnK} {fnMicroc} {fnMicrosoft Sans Serif} {fnMicrosoft Sans Serif} _{1}varphi _{2}r(varphi)},dvarphi \c={1}{2}int _{varphi}int ¿Qué?. ¿Qué? ¿Por qué? _{2}+varphi ¿Por qué? _{2}-varphi _{1}right)end{aligned}}

La espiral de Fermat: área entre arcos vecinos

Después de elevar ambos ángulos en 2π se obtiene

Ā ̄ =a24()φ φ 2+φ φ 1+4π π )()φ φ 2− − φ φ 1)=A¿Qué? ¿Qué? +a2π π ()φ φ 2− − φ φ 1).{displaystyle [overline {}={2}{4}left(varphi _{2}+varphi _{1}+4piright)left(varphi) _{2}-varphi _{1}right)={underline {A}+a^{2}pi left(varphi) _{2}-varphi _{1}right). }

Por lo tanto, el área A de la región entre dos arcos vecinos es

A=a2π π ()φ φ 2− − φ φ 1).{displaystyle A=a^{2}pi left(varphi _{2}-varphi _{1}right). }

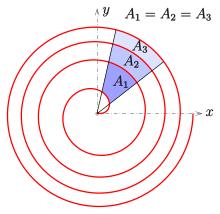
Para el ejemplo que se muestra en el diagrama, todas las franjas vecinas tienen la misma área: A₁ = A₂ = A₃.

Esta propiedad se utiliza en ingeniería eléctrica para la construcción de condensadores variables.

las regiones entre (blanco, azul, amarillo) tienen toda la misma zona, que es igual a la zona del círculo dibujado.

Caso especial debido a Fermat

En 1636, Fermat escribió una carta a Marin Mersenne que contiene el siguiente caso especial:

Sea φ₁ = 0, φ₂ = 2π; entonces el área de la región negra (ver diagrama) es A₀ = a²π², que es la mitad del área del círculo K₀ con radio r(2π). Las regiones entre las curvas vecinas (blanco, azul, amarillo) tienen la misma área A = 2a²π². Por eso:

• El área entre dos arcos de la espiral después de un giro completo equivale a la zona del círculo K₀.

Longitud de arco

La longitud del arco de la espiral de Fermat entre dos puntos (r(φ_i), φ_i) se puede calcular mediante la integral:

L=∫ ∫ φ φ 1φ φ 2()r.. ()φ φ ))2+r2()φ φ )dφ φ =⋯ ⋯ =a2∫ ∫ φ φ 1φ φ 21φ φ +4φ φ dφ φ .{displaystyle {begin{aligned}L ventaja=int _{varphi ¿Qué? ¿Qué? {fnMicrosoft}+4varphis },dvarphi.

Esta integral conduce a una integral elíptica, que se puede resolver numéricamente.

La longitud del arco de la rama positiva de la espiral del Fermat desde el origen también se puede definir por funciones hipergeométricas 2F1⁡ ⁡ ()a,b;c;z){displaystyle operatorname {_{2}F_{1} left(a,,b;,c;,zright)} y la función beta incompleta B⁡ ⁡ ()z;a;b){displaystyle operatorname {B} left(z;,a;,bright)}:

L=a⋅ ⋅ φ φ ⋅ ⋅ 2F1⁡ ⁡ ()− − 12,14;54;− − 4⋅ ⋅ φ φ 2)=a⋅ ⋅ 1− − i8⋅ ⋅ B⁡ ⁡ ()− − 4⋅ ⋅ φ φ 2;14,32){displaystyle {begin{aligned}L ventaja=acdot {sqrt {varphi }cdot operatorname {_{2}F_{1}} left(-{frac {1}{2}},,{frac {1}{4}}};,{frac {5}{4}};,-4cdot varphi ^{2}right)\=acdot {fracdot {fracdot {f}}}cdotcdotcdotcdot {cdot {f}f}}}cdotcdotcdot {cdotc}}cccccccccdotcdotcdotc}cdotc}cdotc}cdot {cccccdotc}fncdotcc}cdotc}cdotcdotcdotc}c}c {1-i}{8}cdot operatorname {B} left(-4cdot varphi ^{2};,{frac {1}{4}}},{frac {3}{2}}}right)end{aligned}}}} {fnunció]

La inversión de la espiral de Fermat (verde) es una espiral de lituo (azul)

Inversión del círculo

La inversión en el círculo unitario tiene en coordenadas polares la descripción simple (r, φ) ↦ (1/r, φ).

• La imagen de la espiral de Fermat r = a√φ bajo la inversión en el círculo de la unidad es una espiral de lituo con ecuación polar
  r=1aφ φ .{displaystyle ;r={frac {1}{a{sqrt {fncipi} - Sí.

  
  Cuando φ = 1/a², ambas curvas se intersectan en un punto fijo en el círculo de la unidad.
• El tangentex-eje) en el punto de inflexión (origin) de la espiral de Fermat se mapea sobre sí mismo y es la línea asintotica de la espiral de lituo.

La proporción áurea y el ángulo áureo

En la filotaxis del disco, como en el girasol y la margarita, la malla de espirales se produce en los números de Fibonacci porque la divergencia (ángulo de sucesión en una sola disposición en espiral) se aproxima a la proporción áurea. La forma de las espirales depende del crecimiento de los elementos generados secuencialmente. En la filotaxis de discos maduros, cuando todos los elementos tienen el mismo tamaño, la forma de las espirales es idealmente la de las espirales de Fermat. Esto se debe a que la espiral de Fermat atraviesa anillos iguales en vueltas iguales. El modelo completo propuesto por H. Vogel en 1979 es

r=cn,Silencio Silencio =n× × 137.508∘ ∘ ,{displaystyle {begin{aligned}r ventaja=c{sqrt {n},\theta < ntimes 137.508^{circ },end{aligned}}}}

donde θ es el ángulo, r es el radio o la distancia desde el centro, y n es el número índice del florete y c es un factor de escala constante. El ángulo 137,508° es el ángulo áureo que se aproxima mediante proporciones de números de Fibonacci.

El patrón de florets producido por el modelo de Vogel (imagen central). Las otras dos imágenes muestran los patrones para valores ligeramente diferentes del ángulo.

El patrón espiral resultante de discos unitarios debe distinguirse de las espirales de Doyle, patrones formados por discos tangentes de radios geométricamente crecientes colocados en espirales logarítmicas.

Plantas solares

También se ha descubierto que la espiral de Fermat es un diseño eficiente para los espejos de las plantas de energía solar concentrada.