Espectroscopia rotacional-vibracional

Espectroscopia rotacional-vibracional es una rama de la espectroscopia molecular que se ocupa de los espectros infrarrojos y Raman de moléculas en fase gaseosa. Las transiciones que implican cambios tanto en estados vibratorios como rotacionales pueden abreviarse como transiciones rovibracionales (o ro-vibracionales). Cuando tales transiciones emiten o absorben fotones (radiación electromagnética), la frecuencia es proporcional a la diferencia en los niveles de energía y puede detectarse mediante ciertos tipos de espectroscopia. Dado que los cambios en los niveles de energía rotacional suelen ser mucho más pequeños que los cambios en los niveles de energía vibratoria, se dice que los cambios en el estado rotacional dan una estructura fina al espectro vibratorio. Para una transición vibratoria dada, el mismo tratamiento teórico que para la espectroscopia rotacional pura proporciona los números cuánticos rotacionales, los niveles de energía y las reglas de selección. En las moléculas superiores lineales y esféricas, las líneas de rotación se encuentran como progresiones simples tanto en frecuencias más altas como más bajas en relación con la frecuencia de vibración pura. En las moléculas superiores simétricas las transiciones se clasifican en paralelas cuando el cambio del momento dipolar es paralelo al eje principal de rotación, y perpendiculares cuando el cambio es perpendicular a ese eje. El espectro ro-vibracional del agua del rotor asimétrico es importante debido a la presencia de vapor de agua en la atmósfera.

Descripción general

La espectroscopia rovibracional se refiere a moléculas en fase gaseosa. Hay secuencias de niveles rotacionales cuantificados asociados tanto con el estado vibratorio fundamental como con el excitado. Los espectros a menudo se resuelven en líneas debido a las transiciones de un nivel rotacional en el estado vibratorio del suelo a un nivel rotacional en el estado vibratorio excitado. Las líneas correspondientes a una determinada transición vibratoria forman una banda.

En los casos más simples, la parte del espectro infrarrojo que involucra transiciones vibratorias con el mismo número cuántico rotacional (ΔJ = 0) en los estados fundamental y excitado se llama rama Q. En el lado de alta frecuencia de la rama Q, la energía de las transiciones rotacionales se suma a la energía de la transición vibratoria. Esto se conoce como rama R del espectro para ΔJ = +1. La rama P para ΔJ = −1 se encuentra en el lado del número de onda bajo de la rama Q. La apariencia de la rama R es muy similar a la apariencia del espectro de rotación puro (pero desplazado a números de onda mucho más altos), y la rama P aparece como una imagen casi especular de la rama R. A veces falta la rama Q debido a que se prohíben las transiciones sin cambios en J.

La apariencia de la estructura fina rotacional está determinada por la simetría de los rotores moleculares que se clasifican, de la misma manera que para la espectroscopia rotacional pura, en moléculas lineales, clases de rotores esféricos, simétricos y asimétricos. El tratamiento de la mecánica cuántica de la estructura fina rotacional es el mismo que para la rotación pura.

La fuerza de una línea de absorción está relacionada con el número de moléculas con los valores iniciales del número cuántico vibracional ν y el número cuántico rotacional J{displaystyle J}Y depende de la temperatura. Ya que en realidad 2J+1{displaystyle 2J+1} estados con número cuántico rotacional J{displaystyle J}, la población con valor J{displaystyle J} aumentos con J{displaystyle J} Inicialmente, y luego decae a más alto J{displaystyle J}. Esto da la forma característica de las ramas P y R.

Una convención general es etiquetar cantidades que se refieren al terreno vibratorio y estados excitados de una transición con doble primo y único, respectivamente. Por ejemplo, la constante de rotación para el estado del suelo está escrita como B.. .. ,{displaystyle B^{primeprime },} y el estado excitado como B.. .{displaystyle B^{prime }Además, estas constantes se expresan en las unidades del espectroscopista molecular de cm⁻¹. así B{displaystyle B} en este artículo corresponde a B̄ ̄ =B/hc{displaystyle {bar {B}=B/hc} en la definición de constante rotacional en el rotor Rigid.

Método de diferencias de combinación

El análisis numérico de los datos espectrales rotacionales parece ser complicado por el hecho de que el número de onda para cada transición depende de dos constantes rotativas, B.. .. {displaystyle B^{primeprime } y B.. {displaystyle B^{prime }. Sin embargo, las combinaciones que dependen de una sola constante de rotación se encuentran substrayendo números de onda de pares de líneas (una en el P-branch y otra en el R-branch) que tienen el mismo nivel inferior o el mismo nivel superior. Por ejemplo, en una molécula diatómica la línea denotó P()J+ 1) se debe a la transición (v= 0, J+ 1) → (v= 1, J) (que significa una transición del estado con número de cuántico vibracional ν va de 0 a 1 y el número de cuántico rotacional va de algún valor J+ 1 a J, con Jy la línea R()J− 1) se debe a la transición (v= 0, J−1) →v= 1,J). La diferencia entre los dos números de onda corresponde a la diferencia energética entre el (J+ 1) y (J− 1) niveles del estado vibracional inferior y es denotado por Δ Δ 2{displaystyle Delta _{2} ya que es la diferencia entre los niveles que difieren por dos unidades de J. Si se incluye la distorsión centrífuga, se da por

Δ Δ 2.. .. F()J)=.. ̄ ̄ ()R()J− − 1))− − .. ̄ ̄ ()P()J+1))=()2B.. .. − − 3D.. .. )()2J+1)− − D.. .. ()2J+1)3{displaystyle Delta _{2}^{primeprime }F(J)={bar {nu }(R(J-1)-{bar {nu }}(P(J+1)=(2B^{primeprimeprime }-3D^{prime prime })left(2J+1right)-D^{prime prime }left(2J+1right)^{3}

Donde .. ̄ ̄ ()){displaystyle {bar {nu}()} significa la frecuencia (o número de onda) de la línea dada. El término principal, 2B.()2J+1),{displaystyle 2B'(2J+1),} viene de la diferencia en la energía de la J+1{displaystyle J+1} estado rotativo, B.()()J+1)()J+2)),{displaystyle B'(J+1)(J+2)),} y la del J− − 1{displaystyle J-1} estado, B.()()J− − 1)J).{displaystyle B'(J-1)J). }

La constante de rotación del estado vibratorio del suelo B′′ y la constante de distorsión centrífuga, D′′ se pueden encontrar ajustando por mínimos cuadrados esta diferencia en función de J. La constante B′′ se utiliza para determinar la distancia internuclear en el estado fundamental como en la espectroscopia rotacional pura. (Ver el Apéndice)

De manera similar, la diferencia R(J) − P(J) depende solo de las constantes B′ y D′ para el estado vibratorio excitado (v = 1), y B′ se puede utilizar para determinar la distancia internuclear en ese estado (que es inaccesible a la espectroscopia rotacional pura).

Δ Δ 2.. F()J)=.. ̄ ̄ ()R()J))− − .. ̄ ̄ ()P()J))=()2B.. − − 3D.. )()2J+1)− − D.. ()2J+1)3{displaystyle Delta _{2}{prime }F(J)={bar {nu }(R(J))-{bar {nu }(P(J)=(2B^{prime }-3D^{prime })left(2J+1right)-D^{prime }left(2J+1right)^{3}

Moléculas lineales

Moléculas diatómicas heteronucleares

Las moléculas diatómicas con la fórmula general AB tienen un modo normal de vibración que implica estiramiento del vínculo A-B. Valores del término vibratorio G()v){displaystyle G(v)}, para un oscilador anarmónico se dan, a una primera aproximación, por

G()v)=⋅ ⋅ e()v+12)− − ⋅ ⋅ eχ χ e()v+12)2{displaystyle G(v)=omega _{e}left(v+{1over 2}right)-omega _{e}chi _{e}left(v+{1over 2}right)^{2},}

donde v es un número cuántico vibratorio, ω_e es el número de onda armónico y χ_e es una constante de anarmonicidad.

Cuando la molécula está en fase gaseosa, puede girar alrededor de un eje, perpendicular al eje molecular, que pasa por el centro de masa de la molécula. La energía rotacional también está cuantificada, con valores de términos en una primera aproximación dados por

Fv()J)=BvJ()J+1)− − DJ2()J+1)2{displaystyle F_{v}(J)=B_{v}Jleft(J+1right)-DJ^{2}left(J+1right)^{2}

donde J es un número cuántico rotacional y D es una constante de distorsión centrífuga. La constante de rotación, B_v depende del momento de inercia de la molécula, I_v, que varía con el número cuántico vibracional, v

Bv=h8π π 2cIv;Iv=mAmBmA+mBdv2{displaystyle B_{v}={h over {8pi ^{2}cI_{v}}}quad I_{v}={frac {m_{A}m_{B} {m_{B}d_{v}} {2}}} {m_{A}} {m_{A}}} {m_{A}}} {c} {c}}} {c}} {c} {c}} {c}}} {c}}}} {c}}}}}}}}}}}}}}}}}} {c}}} {c}}}}}}}}}}}} {cc} {c}}}} {cc}}} {c}}}}}}}}}} {c}}}}}}}}}} {c}}}}}}}}} {c}}}}}}}}}} {cccccc}}}}}}}}}}}} {cc}}}}}}}}}}}}}}}}}}}}}}}}

donde m_A y m_B son las masas de los átomos A y B, y d representa la distancia entre los átomos. Los valores de los términos de los estados ro-vibracionales se encuentran (en la aproximación de Born-Oppenheimer) combinando las expresiones de vibración y rotación.

G()v)+Fv()J)=[⋅ ⋅ e()v+12)+BvJ()J+1)]− − [⋅ ⋅ eχ χ e()v+12)2+DJ2()J+1)2]{displaystyle G(v)+F_{v}(J)=left[omega _{e}left(v+{1over 2}right)+B_{v}J(J+1)right]-left[omega] ¿Por qué?

Los primeros dos términos de esta expresión corresponden a un oscilador armónico y un rotor rígido, el segundo par de términos hace una corrección por anarmonicidad y distorsión centrífuga. Dunham dio una expresión más general.

La regla de selección para el dipolo eléctrico permitió transiciones ro-vibracionales, en el caso de una molécula diamagnética diatómica es

Δ Δ v=± ± 1()± ± 2,± ± 3,etc.{displaystyle Delta v=pm 1 (pm 2,pm 3,{textit {etc.}}}),Δ Δ J=± ± 1{displaystyle),Delta J=pm 1}

La transición con Δv=±1 se conoce como transición fundamental. La regla de selección tiene dos consecuencias.

1. Tanto los números cuánticos vibratorios como rotacionales deben cambiar. La transición:Δ Δ v=± ± 1,Δ Δ J=0{displaystyle Delta v=pm 1,Delta J=0} Está prohibido
2. El cambio energético de la rotación puede ser restado o añadido al cambio energético de la vibración, dando las ramas P y R del espectro, respectivamente.

El cálculo de los números de las ondas de transición es más complicado que para la rotación pura porque la constante de rotación B_. es diferente en el suelo y estados vibratorios excitados. Una expresión simplificada para los números de onda se obtiene cuando las constantes de distorsión centrífuga D.. {displaystyle D^{prime } y D.. .. {displaystyle D^{primeprime } son aproximadamente iguales entre sí.

.. ̄ ̄ =⋅ ⋅ 0+()B.. +B.. .. )m+()B.. − − B.. .. )m2− − 2()D.. +D.. .. )m3,⋅ ⋅ 0=⋅ ⋅ e()1− − 2χ χ e)m=± ± 1,± ± 2etc.{displaystyle {bar} }=omega ¿Por qué? }-B^{primeprime })m^{2}-2(D^{prime }+D^{primeprime})m^{3},quad omega _{0}=omega _{e}(1-2chi _{e})quad m=pm 1,pm 2 etc.}

Donde positivo m los valores se refieren a la R-branch y los valores negativos se refieren al P-branch. El término ω₀ da la posición del (perder) Q-branch, el término ()B.. +B.. .. )m{displaystyle (B^{prime }+B^{primeprime }m} implica una progresión de líneas igualmente espaciadas en las ramas P- y R-, pero el tercer término, ()B.. − − B.. .. )m2{displaystyle (B^{prime - Sí.muestra que la separación entre líneas adyacentes cambia con el número de cuántico rotacional cambiante. Cuando B.. .. {displaystyle B^{primeprime } es mayor que B.. {displaystyle B^{prime }, como suele ser el caso, como J aumenta la separación entre líneas disminuye en el R-branch y aumenta en el P-branch. Análisis de datos del espectro infrarrojo del monóxido de carbono, da valor B.. .. {displaystyle B^{primeprime } de 1.915 cm⁻¹ y B.. {displaystyle B^{prime } de 1.898 cm⁻¹. Las longitudes de unión se obtienen fácilmente de estas constantes como r₀ = 113.3 pm, r₁ = 113.6 pm. Estas longitudes de unión son ligeramente diferentes de la longitud de unión del equilibrio. Esto se debe a que hay energía de cero puntos en el estado del suelo vibratorio, mientras que la longitud del vínculo de equilibrio es al mínimo en la curva de energía potencial. La relación entre las constantes rotativas es dada por

Bv=Beq− − α α ()v+12){displaystyle B_{v}=B_{eq}-alpha left(v+{1 over 2}right)}

donde ν es un número cuántico vibratorio y α es una constante de interacción vibración-rotación que se puede calcular cuando se pueden encontrar los valores B para dos estados vibratorios diferentes. Para monóxido de carbono r_eq = 113,0 pm.

El óxido nítrico, NO, es un caso especial ya que la molécula es paramagnética, con un electrón desapareado. El acoplamiento del momento angular del espín del electrón con la vibración molecular provoca una duplicación lambda con frecuencias armónicas calculadas de 1904,03 y 1903,68 cm⁻¹. Los niveles de rotación también están divididos.

Moléculas diatómicas homonucleares

La mecánica cuántica de las moléculas diatómicas homonucleares, como el dinitrógeno, N₂, y el flúor, F₂, es cualitativamente la misma que la de las moléculas diatómicas heteronucleares, pero la selección Las reglas que rigen las transiciones son diferentes. Dado que el momento dipolar eléctrico de las diatómicas homonucleares es cero, la transición vibratoria fundamental está prohibida por el dipolo eléctrico y las moléculas están inactivas en el infrarrojo. Sin embargo, se puede observar un espectro de N₂ débil permitido por el cuadrupolo cuando se utilizan longitudes de trayectoria largas tanto en el laboratorio como en la atmósfera. Los espectros de estas moléculas se pueden observar mediante espectroscopia Raman porque la vibración molecular está permitida por Raman.

El dioxigeno es un caso especial, ya que la molécula es paramagnética para que se puedan observar transiciones permitidas con dipolo magnético en el infrarrojo. El giro electrónico de la unidad tiene tres orientaciones espaciales con respecto al vector de impulso angular de rotación molecular, N, por lo que cada nivel de rotación se divide en tres estados con impulso angular total (rotación molecular más giro electrónico) J▪ ▪ {displaystyle mathrm {Jhbar } ,}, J = N + 1, N, y N - 1, cada estado J de este llamado triplete tipo p que surge de una orientación diferente del giro con respecto al movimiento rotacional de la molécula. Las reglas de selección para transiciones de dipolo magnético permiten transiciones entre miembros sucesivos del triplet (ΔJ = ±1) de modo que para cada valor del impulso angular rotacional número cuántico N hay dos transiciones permitidas. El ¹⁶El núcleo tiene cero giros nucleares impulso angular, por lo que las consideraciones de simetría exigen que N sólo tenga valores extraños.

Espectros Raman de moléculas diatómicas

La regla de selección es

Δ Δ J=0,± ± 2{displaystyle Delta J=0,pm 2}

de modo que el espectro tenga una rama O (∆J = −2), una rama Q (∆J = 0) y una rama S (∆J=+2). En la aproximación de que B′′ = B′ = B los números de onda vienen dados por

.. ̄ ̄ ()S()J))=⋅ ⋅ 0+4BJ+6B=⋅ ⋅ 0+6B,⋅ ⋅ 0+10B,⋅ ⋅ 0+14B,...{displaystyle {bar {nu}(S(J)=omega _{0}+4BJ+6B=omega _{0}+6B,quad omega _{0}+10B,quad omega 14B, quad...

.. ̄ ̄ ()O()J))=⋅ ⋅ 0− − 4BJ+2B=⋅ ⋅ 0− − 6B,⋅ ⋅ 0− − 10B,⋅ ⋅ 0− − 14B,...{displaystyle {bar {nu}(O(J)=omega _{0}-4BJ+2B=omega _{0}-6B,quad omega 10B, quad omega 14B, quad...

ya que la rama S comienza en J=0 y la rama O en J=2. Entonces, en una primera aproximación, la separación entre S(0) y O(2) es 12B y la separación entre líneas adyacentes en Tanto las ramas O como S son 4B. El efecto más obvio del hecho de que B′′ ≠ B′ es que la rama Q tiene una serie de líneas laterales estrechamente espaciadas en el lado de baja frecuencia debido a transiciones en las que ΔJ=0 para J=1,2, etc. Las fórmulas de diferencia útiles, ignorando la distorsión centrífuga, son las siguientes.

Δ Δ 4.. .. F()J)=.. ̄ ̄ [S()J− − 2)]− − .. ̄ ̄ [O()J+2)]=4B.. .. ()2J+1){displaystyle Delta _{4}^{primeprime }F(J)={bar {nu }[S(J-2)-{bar {nu }}[O(J+2)]=4B^{primeprime }(2J+1)}

Δ Δ 4.. F()J)=.. ̄ ̄ [S()J)]− − .. ̄ ̄ [O()J)]=4B.. ()2J+1){displaystyle Delta _{4}{prime }F(J)={bar {nu }[S(J)]-{bar {nu }[O(J)]=4B^{prime }(2J+1)}

El oxígeno molecular es un caso especial ya que la molécula es paramagnética, con dos electrones desapareados.

Para la diatomía homonuclear, los pesos estadísticos de giro nuclear conducen a intensidades de línea alternadas entre incluso-J.. .. {displaystyle J^{primeprime } y extraño...J.. .. {displaystyle J^{primeprime } niveles. Para la columna nuclear I = 1/2 como en ¹H₂ y ¹⁹F₂ la alternancia de intensidad es 1:3. Para ²H₂ y ¹⁴N₂, I=1 y los pesos estadísticos son 6 y 3 para que el uniforme-J.. .. {displaystyle J^{primeprime } los niveles son dos veces más intensos. Para ¹⁶O₂ ()I=0) todas las transiciones con valores uniformes J.. .. {displaystyle J^{primeprime } están prohibidos.

Moléculas lineales poliatómicas

Estas moléculas se dividen en dos clases, según su simetría: moléculas centrosimétricas con grupo puntual D_∞h, como dióxido de carbono, CO₂ y etino o acetileno, HCCH; y moléculas no centrosimétricas con grupo puntual C_∞v como el cianuro de hidrógeno, HCN y el óxido nitroso, NNO. Las moléculas lineales centrosimétricas tienen un momento dipolar de cero, por lo que no muestran un espectro de rotación puro en las regiones infrarroja o de microondas. Por otro lado, en ciertos estados vibratorios excitados las moléculas tienen un momento dipolar, de modo que se puede observar un espectro rovibracional en el infrarrojo.

Los espectros de estas moléculas se clasifican según la dirección del momento dipole cambio vector. Cuando la vibración induce un cambio de momento dipolo señalando a lo largo del eje molecular el término paralelo se aplica, con el símbolo ∥ ∥ {displaystyle parallel }. Cuando la vibración induce un momento dipolo señalando perpendicular al eje molecular el término perpendicular se aplica, con el símbolo ⊥ ⊥ {displaystyle perp}. En ambos casos los números de onda P- y R- ram siguen la misma tendencia que en moléculas diatómicas. Las dos clases difieren en las reglas de selección que se aplican a las transiciones rotativas. Para las transiciones paralelas, la regla de selección es la misma que para las moléculas diatómicas, es decir, la transición correspondiente al Q-branch está prohibida. Un ejemplo es el modo de estiramiento C-H de cianuro de hidrógeno.

Para una vibración perpendicular se permite la transición ΔJ=0. Esto significa que la transición está permitida para la molécula con el mismo número cuántico rotacional en el suelo y en el estado vibratorio excitado, para todos los estados rotacionales poblados. Esto crea una rama Q intensa y relativamente amplia que consta de líneas superpuestas debido a cada estado de rotación. El modo de flexión N-N-O del óxido nitroso, a ca. 590 cm⁻¹ es un ejemplo.

Los espectros de moléculas centrosimétricas exhiben intensidades de líneas alternas debido a los efectos de simetría del estado cuántico, ya que la rotación de la molécula 180° alrededor de un eje de rotación doble equivale a intercambiar núcleos idénticos. En el dióxido de carbono, los átomos de oxígeno de las especies isotópicas predominantes ¹²C¹⁶O₂ tienen espín cero y son bosones, de modo que la función de onda total debe ser simétrico cuando se intercambian los dos núcleos ¹⁶O. El factor de espín nuclear siempre es simétrico para dos núcleos de espín cero, de modo que el factor de rotación también debe ser simétrico, lo cual es cierto sólo para niveles J pares. Los niveles rotacionales de J impar no pueden existir y las bandas vibratorias permitidas consisten únicamente en líneas de absorción de niveles iniciales de J par. La separación entre líneas adyacentes en las ramas P y R es cercana a 4B en lugar de 2B, ya que faltan líneas alternativas. Para el acetileno, los hidrógenos de ¹H¹²C¹²C¹H tienen espín ½ y son fermiones, por lo que los La función de onda total es antisimétrica cuando se intercambian dos núcleos ¹H. Como ocurre con el hidrógeno orto y para, la función de espín nuclear de los dos hidrógenos tiene tres estados orto simétricos y un estado para antisimétrico. Para los tres estados orto, la función de onda rotacional debe ser antisimétrica correspondiente a J impar, y para el estado para es simétrica correspondiente a J par. Por lo tanto, la población de los niveles J impares es tres veces mayor que la de los niveles J pares. y las intensidades de línea alternativas están en la proporción 3:1.

Moléculas superiores esféricas

Estas moléculas tienen momentos de inercia iguales alrededor de cualquier eje y pertenecen a los grupos de puntos T_d (tetraédrico AX₄) y O_h (octaédrico AX₆). Las moléculas con estas simetrías tienen un momento dipolar de cero, por lo que no tienen un espectro de rotación puro en las regiones infrarroja o de microondas.

Las moléculas tetraédricas como el metano, CH₄, tienen vibraciones de estiramiento y flexión activas en el infrarrojo, pertenecientes al T₂ (a veces escrito como F₂) representación. Estas vibraciones son triplemente degeneradas y los niveles de energía rotacional tienen tres componentes separados por la interacción de Coriolis. Los valores de los términos rotacionales están dados, con una aproximación de primer orden, por

F+=B.. J()J+1)+2B.. Especificaciones Especificaciones r()J+1){displaystyle F^{+}=B_{nu }J(J+1)+2B_{nu }zeta _{r}(J+1)}

F0=B.. J()J+1){displaystyle F^{0}=B_{nu }J(J+1)}

F− − =B.. J()J+1)− − 2B.. Especificaciones Especificaciones r()J+1){displaystyle F^{-}=B_{nu }J(J+1)-2B_{nu }zeta _{r}(J+1)}

Donde Especificaciones Especificaciones r{displaystyle zeta _{r}} es una constante para el acoplamiento de Coriolis. La regla de selección para una vibración fundamental es

Δ Δ J=0,± ± 1{displaystyle Delta J=0,pm 1}

Así, el espectro es muy parecido al espectro de una vibración perpendicular de una molécula lineal, con un fuerte Q-branch compuesto de muchas transiciones en las que el número de cuántica rotacional es el mismo en el suelo vibracional y estados excitados, J.. =J.. .. =1,2...{displaystyle J^{prime - Sí. El efecto del acoplamiento de Coriolis es claramente visible en la vibración de estiramiento C-H del metano, aunque estudio detallado ha demostrado que la fórmula de primer orden para el acoplamiento de Coriolis, dada arriba, no es adecuada para el metano.

Moléculas superiores simétricas

Estas moléculas tienen un eje de rotación principal único del orden 3 o superior. Hay dos momentos distintos de la inercia y por lo tanto dos constantes rotativas. Para la rotación sobre cualquier eje perpendicular al eje único, el momento de la inercia es I⊥ ⊥ {displaystyle I_{perp} y la constante rotacional es B=h8π π 2cI⊥ ⊥ {displaystyle B={h over {8pi ^{2}cI_{perp }En cuanto a las moléculas lineales. Para la rotación sobre el eje único, sin embargo, el momento de la inercia es I∥ ∥ {displaystyle I_{parallel} y la constante rotacional es A=h8π π 2cI∥ ∥ {displaystyle A={h over {8pi ^{2}cI_{parallel }. Ejemplos incluyen amoníaco, NH₃ y metilcloruro, CH₃Cl (tanto de la simetría molecular descrita por el grupo de puntos C_3v), trifluoruro de hierro, BF₃ y fósforo pentacloruro, PCl₅ (tanto del grupo de puntos D_3h), y benceno, C₆H₆ (grupo punto D_6h).

Para rotores simétricos un número cuántico J se asocia con el impulso angular total de la molécula. Para un valor dado de J, hay un 2J+1- degeneración plegable con el número cuántico, M tomando los valores +J...0...J. El tercer número cuántico, K se asocia con la rotación sobre el eje de rotación principal de la molécula. Como con moléculas lineales, las transiciones se clasifican como paralelo, ∥ ∥ {displaystyle parallel } o perpendicular,⊥ ⊥ {displaystyle perp}, en este caso según la dirección del cambio de momento dipole con respecto al eje de rotación principal. Una tercera categoría implica ciertos tonos y bandas combinadas que comparten las propiedades de las transiciones tanto paralelas como perpendiculares. Las reglas de selección son

∥ ∥ {displaystyle parallel } Si K ل 0, luego ΔJ = 0, ±1 y ΔK = 0

Si K = 0, luego ΔJ = ±1 y ΔK = 0

⊥ ⊥ {displaystyle perp} ΔJ = 0, ±1 y ΔK = ±1

El hecho de que las reglas de selección sean diferentes es la justificación de la clasificación y significa que los espectros tienen una apariencia diferente que a menudo puede reconocerse inmediatamente. Se puede dar una expresión para los números de onda calculados de las ramas P y R como

.. ̄ ̄ =.. ̄ ̄ 0+()B.. +B.. .. )m+()B.. − − B.. .. − − DJ.. +DJ.. .. )m2{displaystyle {bar} }={bar {nu }_{0}+(B^{prime }+B^{primeprime })m+(B^{prime }-B^{prime prime. }+D_{J} {primeprime})m^{2}

− − 2()DJ.. +DJ.. .. )m3− − ()DJ.. − − DJ.. .. )m4{displaystyle -2(D_{J}{prime }+D_{J} {primeprime})m^{3}-(D_{J}^{prime - Sí.

+{}[()A.. − − B.. )− − ()A.. .. − − B.. .. )]− − [DJK.. +DJK.. .. ]m− − [DJK.. − − DJK.. .. ]m2}K2− − ()DK.. − − DK.. .. )K4{displaystyle +leftleft[(A^{prime }-B^{prime })-(A^{primeprime }-B^{primeprime })right]-left [D_{JK}{prime }+D_{JK} {prime prime }right]m-left [D_{JK}{prime }-D_{JK}{prime prime }right]m^{2}derecha {2} ¿Qué?

en que m = J+1 para el R-branch y -J para el P-branch. Las tres constantes centrífugas de distorsión DJ,DJK{displaystyle D_{J},D_{JK}, y DK{displaystyle D_{K} son necesarios para ajustar los valores de término de cada nivel. Los números de onda de la subestructura correspondiente a cada banda son dados por

.. ̄ ̄ =.. ̄ ̄ sub+()B.. − − B.. .. )J()J+1)− − ()DJ.. − − DJ.. .. )J2()J+1)2− − ()DJK.. − − DJK.. .. )J()J+1)K2{displaystyle {bar} }={bar {nu }_{sub}+(B^{prime J(J+1)-(D_{J}^{prime J^{2}(J+1)^{2}-(D_{JK}} J(J+1)K^{2}

.. ̄ ̄ sub{displaystyle {bar} } representa el Q-branch de la subestructura, cuya posición es dada por

.. ̄ ̄ sub=.. ̄ ̄ 0+[()A.. − − B.. )− − ()A.. .. − − B.. .. )]K2− − ()DK.. − − DK.. .. )K4{displaystyle {bar} }_{sub}={bar {nu }_{0}+left [(A^{prime }-B^{prime })-(A^{primeprime }-B^{primeprime })right] K^{2}- }-D_{K} {prime prime }K^{4}.

Bandas paralelas

La vibración de estiramiento C-Cl del cloruro de metilo, CH₃Cl, da una banda paralela ya que el cambio del momento dipolar está alineado con el eje de rotación triple. El espectro de líneas muestra con bastante claridad la subestructura de esta banda; en realidad, se necesitaría espectroscopia de muy alta resolución para resolver completamente la estructura fina. Allen y Cross muestran partes del espectro de CH₃D y dan una descripción detallada del análisis numérico de los datos experimentales.

Bandas perpendiculares

La regla de selección para bandas perpendiculares da lugar a más transiciones que con bandas paralelas. Una banda puede verse como una serie de subestructuras, cada una con ramas P, Q y R. Las ramas Q están separadas por aproximadamente 2 (A′-B′). La vibración asimétrica de flexión del HCH del cloruro de metilo es típica. Muestra una serie de intensas ramas Q con una estructura fina rotacional débil. El análisis de los espectros se complica por el hecho de que la vibración del estado fundamental está obligada, por simetría, a ser una vibración degenerada, lo que significa que el acoplamiento de Coriolis también afecta al espectro.

Bandas híbridas

Los armónicos de una vibración fundamental degenerada tienen componentes de más de un tipo de simetría. Por ejemplo, el primer armónico de una vibración perteneciente a la representación E en una molécula como el amoniaco, NH₃, tendrá componentes pertenecientes a A₁ y E representaciones. Una transición al componente A₁ dará una banda paralela y una transición al componente E dará bandas perpendiculares; el resultado es una banda híbrida.

Inversión en amoniaco

Para el amoníaco, NH₃, la vibración de flexión simétrica se observa como dos ramas cerca de 930 cm⁻¹ y 965 cm⁻¹. Esta llamada duplicación por inversión surge porque la vibración de flexión simétrica es en realidad un movimiento de gran amplitud conocido como inversión, en el que el átomo de nitrógeno pasa a través del plano de los tres átomos de hidrógeno, similar a la inversión de un paraguas. La curva de energía potencial para una vibración de este tipo tiene un mínimo doble para las dos geometrías piramidales, de modo que los niveles de energía vibratoria se presentan en pares, que corresponden a combinaciones de los estados vibratorios en los dos mínimos potenciales. Los dos estados v = 1 se combinan para formar un estado simétrico (1⁺) a 932,5 cm⁻¹ sobre el suelo (estado 0⁺) y un estado antisimétrico (1⁻) a 968,3 cm⁻¹.

El estado fundamental vibratorio (v = 0) también se duplica, aunque la diferencia de energía es mucho menor, y la transición entre los dos niveles se puede medir directamente en la región de microondas, a ca. 24 Ghz (0,8 cm⁻¹). Esta transición es históricamente significativa y se utilizó en el máser de amoníaco, el precursor del láser.

Moléculas superiores asimétricas

Las moléculas superiores asimétricas tienen como máximo uno o más ejes de rotación dobles. Hay tres momentos de inercia desiguales alrededor de tres ejes principales mutuamente perpendiculares. Los espectros son muy complejos. Los números de onda de transición no se pueden expresar en términos de una fórmula analítica, pero se pueden calcular utilizando métodos numéricos.

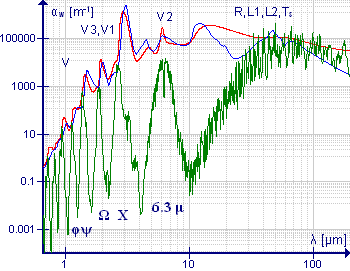
La molécula de agua es un ejemplo importante de esta clase de molécula, particularmente debido a la presencia de vapor de agua en la atmósfera. El espectro de baja resolución que se muestra en verde ilustra la complejidad del espectro. En longitudes de onda superiores a 10 μm (o números de onda inferiores a 1000 cm⁻¹), la absorción se debe a la rotación pura. La banda de alrededor de 6,3 μm (1590 cm⁻¹) se debe a la vibración de flexión HOH; La considerable amplitud de esta banda se debe a la presencia de una extensa estructura fina rotacional. Los espectros de alta resolución de esta banda se muestran en Allen y Cross, p. 221. Las vibraciones de estiramiento simétricas y asimétricas están cercanas entre sí, por lo que las finas estructuras rotacionales de estas bandas se superponen. Las bandas de longitud de onda más corta son armónicos y bandas combinadas, todas las cuales muestran una estructura fina rotacional. Los espectros de resolución media de las bandas alrededor de 1600 cm⁻¹ y 3700 cm⁻¹ se muestran en Banwell y McCash, p91.

Las bandas rovibracionales de moléculas superiores asimétricas se clasifican como tipo A, B o C para transiciones en las que el cambio del momento dipolar se produce a lo largo del eje del momento de inercia más pequeño al más alto.

Métodos experimentales

Los espectros rovibracionales generalmente se miden con alta resolución espectral. En el pasado, esto se lograba utilizando una rejilla de Echelle como elemento de dispersión espectral en un espectrómetro de rejilla. Este es un tipo de rejilla de difracción optimizada para utilizar órdenes de difracción más altos. Hoy en día, en todas las resoluciones, el método preferido es FTIR. La razón principal de esto es que los detectores de infrarrojos son inherentemente ruidosos y FTIR detecta señales sumadas en múltiples longitudes de onda logrando simultáneamente una mayor relación señal/ruido en virtud de la ventaja de Fellgett para los métodos multiplexados. El poder de resolución de un espectrómetro FTIR depende del retardo máximo del espejo en movimiento. Por ejemplo, para lograr una resolución de 0,1 cm⁻¹, el espejo móvil debe tener un desplazamiento máximo de 10 cm desde su posición con una diferencia de trayectoria cero. Connes midió el espectro de vibración-rotación del CO₂ de Venus con esta resolución. Ya está disponible comercialmente un espectrómetro con una resolución de 0,001 cm⁻¹. La ventaja de rendimiento de FTIR es importante para la espectroscopia de alta resolución, ya que el monocromador de un instrumento dispersivo con la misma resolución tendría rendijas de entrada y salida muy estrechas.

Al medir los espectros de gases, es relativamente fácil obtener longitudes de trayectoria muy largas utilizando una celda de reflexión múltiple. Esto es importante porque permite reducir la presión para minimizar el ensanchamiento de presión de las líneas espectrales, lo que puede degradar la resolución. Se encuentran disponibles comercialmente longitudes de camino de hasta 20 m.

Apéndice

El método de diferencias de combinación utiliza diferencias de números de onda en las ramas P y R para obtener datos que dependen únicamente de las constantes de rotación en el estado vibratorio fundamental o excitado. Para el estado excitado