Espacio tangente

En matemáticas, el espacio tangente de una variedad generaliza a dimensiones superiores la noción de planos tangentes a superficies en tres dimensiones y líneas tangentes a curvas en dos dimensiones. En el contexto de la física, el espacio tangente a una variedad en un punto puede verse como el espacio de posibles velocidades para una partícula que se mueve en la variedad.

Descripción informal

Una representación pictórica del espacio tangente de un solo punto ${displaystyle x}$ en una esfera. Un vector en este espacio tangente representa una posible velocidad (de algo que se mueve en la esfera) a ${displaystyle x}$. Después de moverse en esa dirección a un punto cercano, la velocidad sería dada por un vector en el espacio tangente de ese punto, un espacio tangente diferente que no se muestra.

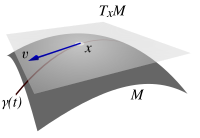
En geometría diferencial, se puede fijar a cada punto ${displaystyle x}$ de un manifold diferente a espacio tangente— un espacio vectorial real que intuitivamente contiene las posibles direcciones en las que uno puede pasar tangencialmente ${displaystyle x}$. Los elementos del espacio tangente en ${displaystyle x}$ son llamados vectores tangentes a ${displaystyle x}$. Esta es una generalización de la noción de un vector, basado en un punto inicial dado, en un espacio euclidiano. La dimensión del espacio tangente en cada punto de un manifold conectado es la misma que la del mismo manifold.

Por ejemplo, si el múltiple dado es un ${displaystyle 2}$- esfera, entonces se puede imaginar el espacio tangente en un punto como el plano que toca la esfera en ese punto y es perpendicular al radio de la esfera a través del punto. En términos más generales, si se piensa en un conjunto dado como un submanifold integrado del espacio euclidiano, entonces se puede imaginar un espacio tangente en esta manera literal. Este fue el enfoque tradicional para definir el transporte paralelo. Muchos autores en geometría diferencial y relatividad general lo utilizan. Más estrictamente, esto define un espacio tangente afine, que es distinto del espacio de vectores tangentes descrito por la terminología moderna.

En la geometría algebraica, en contraste, hay una definición intrínseca de la espacio tangente en un punto de una variedad algebraica ${displaystyle V}$ que da un espacio vectorial con dimensión al menos la de ${displaystyle V}$ en sí mismo. Los puntos ${displaystyle p}$ en la que la dimensión del espacio tangente es exactamente la de ${displaystyle V}$ se llaman non-singular puntos; los otros se llaman singular puntos. Por ejemplo, una curva que se cruza no tiene una línea tangente única en ese punto. Los puntos singulares ${displaystyle V}$ son aquellos donde la "prueba de ser un múltiple" falla. Vea el espacio tangente Zariski.

Una vez que se han introducido los espacios tangentes de una variedad, se pueden definir campos vectoriales, que son abstracciones del campo de velocidad de las partículas que se mueven en el espacio. Un campo vectorial une a cada punto de la variedad un vector del espacio tangente en ese punto, de manera uniforme. Tal campo vectorial sirve para definir una ecuación diferencial ordinaria generalizada en una variedad: una solución a tal ecuación diferencial es una curva diferenciable en la variedad cuya derivada en cualquier punto es igual al vector tangente unido a ese punto por el campo vectorial.

Todos los espacios tangentes de una variedad se pueden "pegar juntos" para formar una nueva variedad diferenciable con el doble de la dimensión de la variedad original, llamada paquete tangente de la variedad.

Definiciones formales

La descripción informal anterior se basa en la capacidad de un múltiples para ser incrustado en un espacio vectorial ambiente ${displaystyle mathbb {R} {} {m}$ para que los vectores tangentes puedan "aflojar" del múltiple en el espacio ambiente. Sin embargo, es más conveniente definir la noción de un espacio tangente basado únicamente en el múltiple.

Hay varias formas equivalentes de definir los espacios tangentes de una variedad. Si bien la definición a través de la velocidad de las curvas es intuitivamente la más simple, también es la más engorrosa para trabajar. A continuación se describen enfoques más elegantes y abstractos.

Definición mediante curvas tangentes

En la imagen incrustada, un vector tangente en un punto ${displaystyle x}$ se piensa como velocidad de una curva que pasa por el punto ${displaystyle x}$. Por lo tanto, podemos definir un vector tangente como una clase de equivalencia de curvas pasando por ${displaystyle x}$ mientras que ser tangente el uno al otro ${displaystyle x}$.

Supongamos que ${displaystyle M}$ es un ${displaystyle C^{k}$ manifold diferente (con suavidad ${displaystyle kgeq 1}$) y eso ${displaystyle xin M}$. Elija un gráfico de coordenadas ${displaystyle varphi: Uto mathbb {R} {fn}$, donde ${displaystyle U}$ es un subconjunto abierto de ${displaystyle M}$ que contiene ${displaystyle x}$. Supongamos más allá que dos curvas ${displaystyle gamma _{1},gamma _{2}:(-1,1)to M}$ con ${displaystyle {gamma}(0)=x={gamma ¿Qué?$ se dan tales que ambos ${displaystyle varphi circ gamma _{1},varphi circ gamma _{2}:(-1,1)to mathbb {R} ^{n}$ son diferentes en el sentido ordinario (los llamamos curvas diferentes inicializadas a ${displaystyle x}$). Entonces... ${displaystyle gamma _{1}$ y ${displaystyle gamma _{2}$ se dice que equivalente a ${displaystyle 0}$ si y sólo si los derivados de ${displaystyle varphi circ gamma ¿Qué?$ y ${displaystyle varphi circ gamma ¿Qué?$ a ${displaystyle 0}$ coincide. Esto define una relación de equivalencia en el conjunto de todas las curvas diferenciables inicializadas ${displaystyle x}$, y las clases de equivalencia de tales curvas se conocen como vectores tangentes de ${displaystyle M}$ a ${displaystyle x}$. La clase de equivalencia de tal curva ${displaystyle gamma }$ es denotado por ${displaystyle gamma '(0)}$. El espacio tangente de ${displaystyle M}$ a ${displaystyle x}$, denotado por ${displaystyle T_{x}M}$, se define entonces como el conjunto de todos los vectores tangentes en ${displaystyle x}$; no depende de la elección de la tabla de coordenadas ${displaystyle varphi: Uto mathbb {R} {fn}$.

El espacio tangente ${displaystyle T_{x}M}$ y un vector tangente ${displaystyle vin T_{x}M}$, a lo largo de una curva ${displaystyle xin M}$.

Para definir las operaciones vectoriales-espacio ${displaystyle T_{x}M}$, usamos un gráfico ${displaystyle varphi: Uto mathbb {R} {fn}$ y definir un mapa ${displaystyle mathrm {d} {varphi} }_{x}:T_{x}Mto mathbb {R} {fn}$ por ${fnMicrosoft Sans Serif} {gnMicrosoft Sans Serif} {fnMicrosoft Sans Serif} {m} {mhm {d} {}} {} {}} {cH0} {cH0} {ccH0} {ccH00FF} {cH0} {cH0}}}}} {cH00}}}}}}}}}}}}}}}}}}cccccH00}}}}}}cccccccccccccccccccH00cH00cH00cH00cccH00cH00cH00cH00cH00cH00cH00cH00cH00ccH00cH00cH00}}}}}cH$ Donde ${displaystyle gamma in gamma '(0)}$. El mapa ${displaystyle mathrm {d} {varphi }_{x}$ resulta ser bijetivo y se puede utilizar para transferir las operaciones vectoriales en ${displaystyle mathbb {R} {} {}} {fn}}$ sobre ${displaystyle T_{x}M}$, convirtiendo así a este último en un ${displaystyle n}$-dimensional espacio vectorial real. Una vez más, hay que comprobar que esta construcción no depende del gráfico particular ${displaystyle varphi: Uto mathbb {R} {fn}$ y la curva ${displaystyle gamma }$ ser usado, y de hecho no lo hace.

Definición a través de derivaciones

Supongamos ahora que ${displaystyle M}$ es un ${displaystyle C^{infty }$ Manifold. Una función de valor real ${displaystyle f:Mto mathbb {R}$ se dice que pertenece a ${displaystyle {C^{infty}(M)}$ si y sólo si por cada tabla de coordenadas ${displaystyle varphi: Uto mathbb {R} {fn}$, el mapa ${displaystyle fcirc varphi ^{-1}:varphi [U]subseteq mathbb {R} {n}to mathbb {R}$ es infinitamente diferente. Note que ${displaystyle {C^{infty}(M)}$ es un álgebra asociativa real con respecto al producto de punta y la suma de funciones y la multiplicación del escalar.

A derivación a ${displaystyle xin M}$ se define como un mapa lineal ${displaystyle D:{C^{infty }(M)to mathbb {R}$ que satisface la identidad de Leibniz

$${displaystyle forall f,gin {infty }(M):qquad D(fg)=D(f)cdot g(x)+f(x)cdot D(g),}$$

(Por cada función idénticamente constante ${displaystyle f={text{const}}$ sigue que ${displaystyle D(f)=0}$).

Denote ${displaystyle T_{x}M}$ el conjunto de todas las derivaciones en ${displaystyle x.}$ Ajuste

• ${displaystyle (D_{1}+D_{2})(f):={D}_{1}(f)+{D}_{2}(f)}$ y
• ${displaystyle (lambda cdot D)(f):=lambda cdot D(f)}$

turnos ${displaystyle T_{x}M}$ en un espacio vectorial.

Generalizaciones

Las generalizaciones de esta definición son posibles, por ejemplo, a múltiples complejos y variedades algebraicas. Sin embargo, en lugar de examinar derivaciones ${displaystyle D}$ desde el álgebra completa de funciones, uno debe trabajar en el nivel de gérmenes de funciones. La razón de esto es que la hoja de estructura puede no estar bien para tales estructuras. Por ejemplo, vamos ${displaystyle X}$ ser una variedad algebraica con hoja de estructura ${displaystyle {fnMitcal}} {fnMicrosoft}} {fnMicrosoft Sans Serif}$. Luego el espacio tangente Zariski en un punto ${displaystyle pin X}$ es la colección de todos ${displaystyle mathbb {k}$-derivaciones ${displaystyle D:{mathcal {O}_{X,p}to mathbb {k}$, donde ${displaystyle mathbb {k}$ es el campo de tierra y ${fnMicrosoft Sans Serif}$ es el tallo de ${displaystyle {fnMitcal}} {fnMicrosoft}} {fnMicrosoft Sans Serif}$ a ${displaystyle p}$.

Equivalencia de las definiciones

Para ${displaystyle xin M}$ y una curva diferenciable ${displaystyle gamma:(-1,1)to M}$ tales que ${displaystyle gamma (0)=x,}$ definir ${displaystyle {D_{gamma}(f):=(fcirc gamma)'(0)}$ (donde el derivado se toma en el sentido ordinario porque ${displaystyle fcirc gamma }$ es una función ${displaystyle (-1,1)}$ a ${displaystyle mathbb {R}$). Uno puede determinar que ${displaystyle D_{gamma}(f)}$ es una derivación en el punto ${displaystyle x,}$ y que curvas equivalentes producen la misma derivación. Así, para una clase de equivalencia ${displaystyle gamma '(0),}$ podemos definir ${displaystyle {D_{gamma}(f):=(fcirc gamma)'(0),}$ donde la curva ${displaystyle gamma in gamma '(0)}$ ha sido elegido arbitrariamente. El mapa ${displaystyle gamma '(0)mapsto D_{gamma '(0)}$ es un isomorfismo espacial vectorial entre el espacio de las clases de equivalencia ${displaystyle gamma '(0)}$ y el de las derivaciones en el punto ${displaystyle x.}$

Definición mediante espacios cotangentes

Una vez más, empezamos con un ${displaystyle C^{infty }$ Manifold ${displaystyle M}$ y un punto ${displaystyle xin M}$. Considere el ideal ${displaystyle Yo...$ de ${displaystyle C^{infty}(M)}$ que consiste en todas las funciones suaves ${displaystyle f}$ desvanecerse ${displaystyle x}$, es decir, ${displaystyle f(x)=0}$. Entonces... ${displaystyle Yo...$ y ${displaystyle I^{2}$ ambos son espacios vectoriales reales, y el espacio cociente ${displaystyle I/I^{2}$ se puede demostrar que es isomorfo al espacio cotangente ${displaystyle T_{x} {}M}$ a través del uso del teorema de Taylor. El espacio tangente ${displaystyle T_{x}M}$ entonces se puede definir como el espacio dual ${displaystyle I/I^{2}$.

Si bien esta definición es la más abstracta, también es la más fácilmente transferible a otros entornos, por ejemplo, a las variedades consideradas en geometría algebraica.

Si ${displaystyle D}$ es una derivación en ${displaystyle x}$, entonces ${displaystyle D(f)=0}$ para todos ${displaystyle fin I^{2}$, lo que significa que ${displaystyle D}$ da lugar a un mapa lineal ${displaystyle I/I^{2}to mathbb {R}$. Por el contrario, si ${displaystyle r:I/I^{2}to mathbb {R}$ es un mapa lineal, entonces ${displaystyle D(f):=rleft(f-f(x)+I^{2}right)}$ define una derivación en ${displaystyle x}$. Esto produce una equivalencia entre espacios tangentes definidos a través de derivaciones y espacios tangentes definidos a través de espacios cotangentes.

Propiedades

Si ${displaystyle M}$ es un subconjunto abierto de ${displaystyle mathbb {R} {} {}} {fn}}$, entonces ${displaystyle M}$ es un ${displaystyle C^{infty }$ manifold in a natural manner (take coordinate charts to be identity maps on open subsets of ${displaystyle mathbb {R} {} {}} {fn}}$), y los espacios tangentes son identificados naturalmente con ${displaystyle mathbb {R} {} {}} {fn}}$.

Vectores tangentes como derivadas direccionales

Otra manera de pensar en vectores tangentes es como derivados direccionales. Dado un vector ${displaystyle v}$ dentro ${displaystyle mathbb {R} {} {}} {fn}}$, uno define el derivado direccional correspondiente en un punto ${displaystyle xin mathbb {R} {fn}$ por

${displaystyle forall fin {infty}(mathbb {R} ^{n}):qquad (D_{v}f)(x):=left.{frac {mathrm {d} {fnMicrosoft Sans Serif} {fnMicrosoft Sans Serif} {fnMicrosoft Sans Serif} ¿Por qué?$

Este mapa es naturalmente una derivación en ${displaystyle x}$. Además, cada derivación en un punto en ${displaystyle mathbb {R} {} {}} {fn}}$ es de esta forma. Por lo tanto, hay una correspondencia entre vectores (pensamiento de vectores tangentes en un punto) y derivaciones en un punto.

Como vectores tangentes a un conjunto general en un punto se puede definir como derivaciones en ese punto, es natural pensar en ellos como derivados direccionales. Específicamente, si ${displaystyle v}$ es un vector tangente ${displaystyle M}$ en un momento ${displaystyle x}$ (pensado como derivación), luego definir el derivado direccional ${displaystyle D_{v}$ en la dirección ${displaystyle v}$ por

${displaystyle forall fin {infty}(M):qquad {D_{v}(f):=v(f).}$

Si pensamos en ${displaystyle v}$ como la velocidad inicial de una curva diferenciable ${displaystyle gamma }$ inicializada ${displaystyle x}$, es decir, ${displaystyle v=gamma '(0)}$, entonces en cambio, definir ${displaystyle D_{v}$ por

${displaystyle forall fin {infty}(M):qquad {D_{v}(f):=(fcirc gamma)'(0).}$

Base del espacio tangente en un punto

Para un ${displaystyle C^{infty }$ Manifold ${displaystyle M}$, si un gráfico ${displaystyle varphi =(x^{1},ldotsx^{n}): Uto mathbb {R} {fn}$ se da con ${displaystyle pin U}$, entonces uno puede definir una base ordenada ${textstyle left{left.{frac {partial }{partial x^{1}}}right sobre la vida_{p},dotsleft.{frac {partial }{partial x^{n}}}}right sobre la vida_{}derecha}}}}}}}$ de ${displaystyle T_{p}M}$ por

${displaystyle forall iin {1,ldotsn},~forall fin {C^{infty }(M):qquad {left.{frac {partial }{partial x^{i}}}}}right perpetua_{p}}}=left({fracfracf} {f}{f}}}{f}{f}}{f}}}{f}}}}}}}}}}}}}}}}{f}{f}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}} ¿Qué? Big (}fcirc varphi ^{-1}{Big)}{Big (}varphi (p){Big)}.}$

Entonces por cada vector tangente ${displaystyle vin T_{p}M}$, uno tiene

${displaystyle v=sum _{i=1}v^{i}left.{frac} {partial }{partial "Justo en la vida"$

Por lo tanto, esta fórmula expresa ${displaystyle v}$ como una combinación lineal de la base vectores tangentes ${textstyle left.{frac {partial }{partial x^{i}}right imper_{p}in T_{p}M}$ definido por el gráfico de coordenadas ${displaystyle varphi: Uto mathbb {R} {fn}$.

La derivada de un mapa

Cada mapa suave (o diferente) ${displaystyle varphi:Mto N}$ entre los manifolds lisos (o diferenciables) induce mapas lineales naturales entre sus espacios tangentes correspondientes:

${displaystyle mathrm {d} {varphi} No.$

Si el espacio tangente se define a través de curvas diferenciables, entonces este mapa se define por

${displaystyle {mathrm {} {varphi }_{x}(gamma '(0)):=(varphi circ gamma)'(0).}$

Si, en cambio, el espacio tangente se define a través de derivaciones, entonces este mapa se define por

${displaystyle [mathrm {d} {varphi }_{x}(D)](f):=D(fcirc varphi). }$

El mapa lineal ${displaystyle mathrm {d} {varphi }_{x}$ se llama diversamente derivados, total derivative, diferencial, o adelante de ${displaystyle varphi }$ a ${displaystyle x}$. Se expresa con frecuencia utilizando una variedad de otras notaciones:

${displaystyle Dvarphi _{x},qquad (varphi _{*})_{x},qquad varphi '(x).}$

En cierto sentido, el derivado es la mejor aproximación lineal a ${displaystyle varphi }$ cerca ${displaystyle x}$. Note que cuando ${displaystyle N=Mathbb {R}$, entonces el mapa ${displaystyle mathrm {d} {varphi} }_{x}:T_{x}Mto mathbb {R}$ coincide con la noción habitual del diferencial de la función ${displaystyle varphi }$. En las coordenadas locales el derivado de ${displaystyle varphi }$ es dado por el Jacobiano.

Un resultado importante con respecto al mapa derivado es el siguiente:

Esta es una generalización del teorema de la función inversa a mapas entre variedades.