Espacio de cinco dimensiones
Un espacio de cinco dimensiones es un espacio con cinco dimensiones. En matemáticas, una secuencia de N números puede representar una ubicación en un espacio N-dimensional. Si se interpreta físicamente, es una dimensión más que las tres dimensiones espaciales habituales y la cuarta dimensión del tiempo utilizadas en la física relativista. Si el universo tiene cinco dimensiones o no es un tema de debate.
Física
Gran parte de los primeros trabajos sobre el espacio de cinco dimensiones tenían como objetivo desarrollar una teoría que unificara las cuatro interacciones fundamentales en la naturaleza: fuerzas nucleares fuertes y débiles, gravedad y electromagnetismo. El matemático alemán Theodor Kaluza y el físico sueco Oskar Klein desarrollaron de forma independiente la teoría de Kaluza-Klein en 1921, que utilizaba la quinta dimensión para unificar la gravedad con la fuerza electromagnética. Aunque más tarde se descubrió que sus enfoques eran al menos parcialmente inexactos, el concepto proporcionó una base para futuras investigaciones durante el siglo pasado.
Para explicar por qué esta dimensión no sería directamente observable, Klein sugirió que la quinta dimensión se enrollaría en un bucle pequeño y compacto del orden de 10-33 centímetros. Según su razonamiento, imaginó la luz como una perturbación causada por ondulaciones en la dimensión superior más allá de la percepción humana, similar a cómo los peces en un estanque sólo pueden ver sombras de ondulaciones en la superficie del agua causadas por las gotas de lluvia. Si bien no es detectable, implicaría indirectamente una conexión entre fuerzas aparentemente no relacionadas. La teoría de Kaluza-Klein experimentó un resurgimiento en la década de 1970 debido al surgimiento de la teoría de supercuerdas y la supergravedad: el concepto de que la realidad está compuesta de hebras vibrantes de energía, un postulado sólo matemáticamente viable en diez dimensiones o más. Luego, la teoría de supercuerdas evolucionó hacia un enfoque más generalizado conocido como teoría M. La teoría M sugirió una dimensión extra potencialmente observable además de las diez dimensiones esenciales que permitirían la existencia de supercuerdas. Las otras 10 dimensiones están compactadas o "enrolladas" hasta un tamaño por debajo del nivel subatómico. La teoría de Kaluza-Klein hoy se considera esencialmente una teoría de calibre, siendo el calibre el grupo de círculos.
La quinta dimensión es difícil de observar directamente, aunque el Gran Colisionador de Hadrones brinda la oportunidad de registrar evidencia indirecta de su existencia. Los físicos teorizan que las colisiones de partículas subatómicas producen a su vez nuevas partículas como resultado de la colisión, incluido un gravitón que escapa de la cuarta dimensión, o brana, y se filtra hacia una masa de cinco dimensiones. La teoría M explicaría la debilidad de la gravedad en relación con otras fuerzas fundamentales de la naturaleza, como se puede ver, por ejemplo, cuando se utiliza un imán para levantar un alfiler de una mesa: el imán supera con facilidad la atracción gravitacional de toda la Tierra. .
A principios del siglo XX se desarrollaron enfoques matemáticos que consideraban la quinta dimensión como una construcción teórica. Estas teorías hacen referencia al espacio de Hilbert, un concepto que postula un número infinito de dimensiones matemáticas para permitir un número ilimitado de estados cuánticos. Einstein, Bergmann y Bargmann intentaron más tarde extender el espacio-tiempo cuatridimensional de la relatividad general a una dimensión extrafísica para incorporar el electromagnetismo, aunque no tuvieron éxito. En su artículo de 1938, Einstein y Bergmann estuvieron entre los primeros en introducir el punto de vista moderno de que una teoría tetradimensional, que coincide con la teoría de Einstein-Maxwell a largas distancias, se deriva de una teoría pentadimensional con simetría completa en las cinco dimensiones. . Sugirieron que el electromagnetismo era el resultado de un campo gravitacional "polarizado" en la quinta dimensión.
La principal novedad de Einstein y Bergmann fue considerar seriamente la quinta dimensión como una entidad física, en lugar de una excusa para combinar el tensor métrico y el potencial electromagnético. Pero luego renegaron y modificaron la teoría para romper su simetría de cinco dimensiones. Su razonamiento, como lo sugirió Edward Witten, era que la versión más simétrica de la teoría predecía la existencia de un nuevo campo de largo alcance, uno que era a la vez sin masa y escalar, lo que habría requerido una modificación fundamental de la teoría de Einstein. de la relatividad general. El espacio de Minkowski y las ecuaciones de Maxwell en el vacío pueden integrarse en un tensor de curvatura de Riemann de cinco dimensiones.
En 1993, el físico Gerard 't Hooft propuso el principio holográfico, que explica que la información sobre una dimensión extra es visible como una curvatura en un espacio-tiempo con una dimensión menos. Por ejemplo, los hologramas son imágenes tridimensionales colocadas sobre una superficie bidimensional, lo que le da a la imagen una curvatura cuando el observador se mueve. De manera similar, en la relatividad general, la cuarta dimensión se manifiesta en tres dimensiones observables como la trayectoria de curvatura de una partícula infinitesimal (de prueba) en movimiento. 'T Hooft ha especulado que la quinta dimensión es en realidad el "tejido del espacio-tiempo".
Investigaciones recientes sugieren varias interpretaciones alternativas de la extensión 5D del espacio-tiempo, la mayoría de ellas generalizando la teoría anterior de Kaluza-Klein. El primer enfoque es el espacio-tiempo-materia, que utiliza un grupo ilimitado de transformaciones de coordenadas 5D para derivar nuevas soluciones de las ecuaciones de campo de Einstein que concuerdan con las correspondientes soluciones clásicas en el espacio-tiempo 4D. Otra representación 5D describe la física cuántica desde una perspectiva de conjunto térmico-espacio-temporal y establece conexiones con la teoría de campos clásica como casos límite. Otro enfoque más, la representación spacekime, eleva el tiempo ordinario de un número real positivo que ordena eventos a un tiempo complejo (kime), que transforma efectivamente los procesos longitudinales de series temporales en variedades 2D (superficies kime).
Geometría de quinta dimensión
Según la definición de Klein, "una geometría es el estudio de las propiedades invariantes de un espacio-tiempo, bajo transformaciones dentro de sí mismo." Por tanto, la geometría de la quinta dimensión estudia las propiedades invariantes de dicho espacio-tiempo, a medida que nos movemos en él, expresadas en ecuaciones formales. La geometría de quinta dimensión generalmente se representa utilizando 5 valores de coordenadas (x,y,z,w,v), donde moverse a lo largo del eje v implica moverse entre diferentes hipervolúmenes.
Politopos
En cinco o más dimensiones, sólo existen tres politopos regulares. En cinco dimensiones, son:
- El 5-simplex de la familia simple, {3,3,3,3}, con 6 vértices, 15 bordes, 20 caras (cada un triángulo equilátero), 15 células (cada una tetraedro regular), y 6 hipercelsas (cada una 5 celdas).
- El 5-cube de la familia hipercubina, {4,3,3,3}, con 32 vértices, 80 bordes, 80 caras (cada una plaza), 40 células (cada una cubo), y 10 hipercelulares (cada uno).
- El 5-orthoplex de la familia de politopos cruzados, {3,3,3,4}, con 10 vértices, 40 bordes, 80 caras (cada uno de los triángulos), 80 células (cada una tetraedro), y 32 hipercelsas (cada una 5 celda).
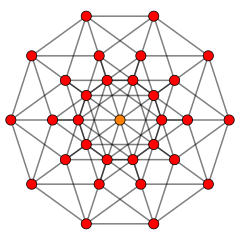
Un uniforme importante 5-polytope es el 5-demicube, h{4,3,3} tiene la mitad de los vértices de los 5-cubos (16), atado por hipercélulas de 5 celdas y 16 celdas alternadas. El expandido o estericado 5-simplex es la figura del vértice de la celosía A5, 
. Tiene una simetría doble de su diagrama de Coxeter simétrico. El número de besos de la celosía, 30, está representado en sus vértices. El rectificado 5-orthoplex es la figura del vértice de la celosía D5, 
. Sus 40 vértices representan el número de besos de la celosía y el más alto para la dimensión 5.
| A5 | Aut (A5) | B5 | D5 | ||
|---|---|---|---|---|---|
 5-simplex {3,3,3,3} |  Stericated 5-simplex | 5-cube  {4,3,3,3} |  5-orthoplex {3,3,3,4} |  Rectificado 5 orthoplex r{3,3,3,4} |  5-demicube  h{4,3,3,3} |
Hiperesfera
Una hiperesfera en el espacio 5 (también llamada 4-esfera debido a que su superficie es de 4 dimensiones) consiste en el conjunto de todos los puntos en el espacio 5 a una distancia fija r desde un punto central P, que es rotacionalmente simétrico. El hipervolumen encerrado por esta hipersuperficie es:
