Espacio de banach

Ajustar Compartir Imprimir Citar

Espacio vectorial Normed que es completo

En matemáticas, más específicamente en análisis funcional, un espacio de Banach (pronunciado [ˈbanax]) es un espacio vectorial normado completo. Así, un espacio de Banach es un espacio vectorial con una métrica que permite calcular la longitud del vector y la distancia entre vectores y es completo en el sentido de que una sucesión de vectores de Cauchy siempre converge a un límite bien definido que está dentro del espacio.

Los espacios de Banach llevan el nombre del matemático polaco Stefan Banach, quien introdujo este concepto y lo estudió sistemáticamente entre 1920 y 1922 junto con Hans Hahn y Eduard Helly. Maurice René Fréchet fue el primero en utilizar el término "espacio de Banach" y Banach, a su vez, acuñó el término "espacio de Fréchet". Los espacios de Banach surgieron originalmente del estudio de los espacios funcionales de Hilbert, Fréchet y Riesz a principios de siglo. Los espacios de Banach juegan un papel central en el análisis funcional. En otras áreas de análisis, los espacios bajo estudio son a menudo espacios de Banach.

Definición

A Banach space es un espacio completo ${displaystyle (X,|cdot |).}$ Un espacio normal es un par $(X,|cdot |)$ que consiste en un espacio vectorial $X$ sobre un campo de escalar $mathbb {K}$ (donde) $mathbb {K}$ es común $mathbb {R}$ o $mathbb{C}$ ) junto con un distinguido norma ${displaystyle |cdot |:Xto mathbb {R}.}$ Como todas las normas, esta norma induce una traducción invariante función de distancia, llamada canónica métrica inducida, definida por

{displaystyle d(x,y):=|y-x|=|x-y|}

{displaystyle x,yin X.}

X

{displaystyle (X,d).}

{displaystyle x_{bullet }=left(x_{n}right)_{n=1}^{infty }}

$d$ -CauchyCauchy $(X,d)$ $|cdot |$ -Cauchy

0,}" xmlns="http://www.w3.org/1998/Math/MathML">r■0,{displaystyle r confía0,}0,}" aria-hidden="true" class="mwe-math-fallback-image-inline" src="https://wikimedia.org/api/rest_v1/media/math/render/svg/72ee1bdad381ab757caae14bc628dd1f9005fa5f" style="vertical-align: -0.671ex; width:5.956ex; height:2.509ex;"/>

N

<math alttext="{displaystyle dleft(x_{n},x_{m}right)=left|x_{n}-x_{m}right|d()xn,xm)=.xn− − xm..r{displaystyle dleft(x_{n},x_{m}right)=left habitx_{n}-x_{m}rightpresionar<img alt="{displaystyle dleft(x_{n},x_{m}right)=left|x_{n}-x_{m}right|

m

n

{displaystyle N.}

d

métrica completa

(X,d)

espacio métrico completo

d

- secuencia de caucho

{displaystyle x_{bullet }=left(x_{n}right)_{n=1}^{infty }}

{displaystyle (X,d),}

xin X

{displaystyle lim _{nto infty }left|x_{n}-xright|=0}

{displaystyle left|x_{n}-xright|=dleft(x_{n},xright),}

x

{displaystyle lim _{nto infty }x_{n}=x;{text{ in }}(X,d).}

L-semi-producto interior

Para cualquier espacio normal ${displaystyle (X,|cdot |),}$ existe un producto L-semi-inner $langle cdotcdot rangle$ on $X$ tales que ${textstyle |x|={sqrt {langle x,xrangle }}}$ para todos $xin X$ ; en general, puede haber infinitamente muchos productos L-semi-inner que satisfacen esta condición. Los productos L-semi-inner son una generalización de productos internos, que son lo que distingue fundamentalmente los espacios de Hilbert de todos los otros espacios de Banach. Esto demuestra que todos los espacios ordenados (y por lo tanto todos los espacios de Banach) pueden ser considerados como generalizaciones de (pre-)Hilbert espacios.

Caracterización en términos de serie

La estructura espacial vectorial permite relacionar el comportamiento de secuencias Cauchy con la de convergiendo series de vectores. Un espacio normal $X$ es un espacio de Banach si y sólo si cada serie absolutamente convergente en $X$ convergencias en $X,$

<math alttext="{displaystyle sum _{n=1}^{infty }|v_{n}|.. n=1JUEGO JUEGO .. vn.. .JUEGO JUEGO implica que.. n=1JUEGO JUEGO vnconvergencias enX.{displaystyle sum _{n=1}{infty } Anteriorv_{n} infty quad {text{ implica que }quad sum _{n=1}{infty }v_{n}\fn} {text{ converge in } X.}<img alt="{displaystyle sum _{n=1}^{infty }|v_{n}|

Topología

La métrica canónica $d$ of a normed space $(X, |cdot|)$ induce la topología métrica habitual ${displaystyle tau _{d}}$ on $X,$ que se denomina canónica o topología inducida por norma. Cada espacio normalizado se asume automáticamente para llevar esta topología de Hausdorff, a menos que se indique lo contrario. Con esta topología, cada espacio de Banach es un espacio de Baire, aunque existen espacios ordenados que son Baire pero no Banach. La norma ${displaystyle |,cdot ,|:left(X,tau _{d}right)to mathbb {R} }$ es siempre una función continua con respecto a la topología que induce.

Las bolas abiertas y cerradas de radio $0}" xmlns="http://www.w3.org/1998/Math/MathML">r■0{displaystyle r] 0" aria-hidden="true" class="mwe-math-fallback-image-inline" src="https://wikimedia.org/api/rest_v1/media/math/render/svg/23cbbcd53bd13620bc53490e3eec42790850b452" style="vertical-align: -0.338ex; width:5.31ex; height:2.176ex;"/>$ centrado en un punto $xin X$ son, respectivamente, los conjuntos

<math alttext="{displaystyle B_{r}(x):={zin X:|z-x|Br()x):={}z▪ ▪ X:.. z− − x.. .r}yCr()x):={}z▪ ▪ X:.. z− − x.. ≤ ≤ r}.{displaystyle B_{r}(x):={zin X:fnMicrosoft Sans: X: 'Princez-x 'Principal'<img alt="{displaystyle B_{r}(x):={zin X:|z-x|

X,

X

x_{0}

sneq 0

{displaystyle x_{0}+sB_{r}(x)=B_{|s|r}left(x_{0}+sxright)qquad {text{ and }}qquad x_{0}+sC_{r}(x)=C_{|s|r}left(x_{0}+sxright).}

{displaystyle s:=1}

xin X

{displaystyle Ssubseteq X,}

S

X

{displaystyle x+S:={x+s:sin S}.}

0right},qquad left{C_{r}(0):r>0right},qquad left{B_{r_{n}}(0):nin mathbb {N} right},qquad {text{ or }}qquad left{C_{r_{n}}(0):nin mathbb {N} right}}" display="block" xmlns="http://www.w3.org/1998/Math/MathML">{}Br()0):r■0},{}Cr()0):r■0},{}Brn()0):n▪ ▪ N},o{}Crn()0):n▪ ▪ N}{fn} {fn} {fn} {fn} {fn} {fn} {fn} {fn}}cfn} {fn} {fn} {fn} {fn} {fn}} {fn}f}}cH00} {fnh}}}f} {f}}f}}}}}}}cccf}cccccccccc}ccccccH00}ccccc}c}c}c}cH00}cH00}cccc}cc}ccccccc}cH00}cH00}cH00}cH00}cH00}ccc}cc}cH0right},qquad left{C_{r}(0):r>0right},qquad left{B_{r_{n}}(0):nin mathbb {N} right},qquad {text{ or }}qquad left{C_{r_{n}}(0):nin mathbb {N} right}}" aria-hidden="true" class="mwe-math-fallback-image-display" src="https://wikimedia.org/api/rest_v1/media/math/render/svg/ac72d9a24a82aefe3282e6fefb1632798dfd700a" style="vertical-align: -0.838ex; width:90.524ex; height:2.843ex;"/>

{displaystyle left(r_{n}right)_{n=1}^{infty }}

{displaystyle 0}

mathbb {R}

{displaystyle r_{n}:=1/n}

{displaystyle r_{n}:=1/2^{n}}

U

X

{displaystyle U=bigcup _{xin I}B_{r_{x}}(x)=bigcup _{xin I}x+B_{r_{x}}(0)=bigcup _{xin I}x+r_{x}B_{1}(0)}

{displaystyle Isubseteq U,}

r_{x}

{displaystyle r_{x}={tfrac {1}{n_{x}}}}

0}" xmlns="http://www.w3.org/1998/Math/MathML">nx■0{displaystyle n_{x}0}0}" aria-hidden="true" class="mwe-math-fallback-image-inline" src="https://wikimedia.org/api/rest_v1/media/math/render/svg/65bea62058b4dbf392d184c2ba7e32c50f88b182" style="vertical-align: -0.671ex; width:6.828ex; height:2.509ex;"/>

I

r_{x}

I

X

espacio separable

X

{textstyle prod _{iin mathbb {N} }mathbb {R} }

mathbb {R}

ell

² secuencia espacial

{displaystyle ell ^{2}(mathbb {N})}

{displaystyle |cdot |_{2},}

{displaystyle ell ^{2}(mathbb {N})}

{displaystyle left{xin ell ^{2}(mathbb {N}):|x|_{2}=1right}.}

Hay un subconjunto compacto $S$ de ${displaystyle ell ^{2}(mathbb {N})}$ cuyo casco convexo ${displaystyle operatorname {co} (S)}$ es no cerrado y así también no compacto (ver esta nota de pie de página por ejemplo). Sin embargo, como en todos los espacios de Banach, el casco convexo cerrado ${displaystyle {overline {operatorname {co} }}S}$ de este subconjunto compacto (y cada otro) será compacto. Pero si un espacio normal no es completo entonces es en general no garantizados ${displaystyle {overline {operatorname {co} }}S}$ será compacto cuando sea $S$ es; un ejemplo puede incluso ser encontrado en un (no-completo) pre-Hilbert vector subespacio de ${displaystyle ell ^{2}(mathbb {N}).}$

Esta topología inducida por la norma también hace ${displaystyle left(X,tau _{d}right)}$ en lo que se conoce como un espacio vectorial topológico (TVS), que por definición es un espacio vectorial dotado de una topología que hace que las operaciones de la adición y la multiplicación del escalar continúen. Se subraya que el TVS ${displaystyle left(X,tau _{d}right)}$ es sólo un espacio vectorial junto con un cierto tipo de topología; es decir, cuando se considera como TVS, es no asociado con cualquiera norma particular o métrica (ambos "perdonados"). Este Hausdorff TVS ${displaystyle left(X,tau _{d}right)}$ es incluso localmente convexo porque el conjunto de todas las bolas abiertas centradas en el origen forma una base de barrio en el origen que consiste en conjuntos abiertos equilibrados convexo. Este TVS también es normable, que por definición se refiere a cualquier TVS cuya topología es inducida por alguna norma (posiblemente desconocida).

Comparación de topologías vectoriales metrizables completas

El teorema de mapeo abierto implica que si ${displaystyle tau {text{ and }}tau _{2}}$ son topologías en $X$ que hacen ambos $(X, tau)$ y ${displaystyle left(X,tau _{2}right)}$ y si una topología es más fina o más gruesa que la otra, entonces deben ser iguales (es decir, si ${displaystyle tau subseteq tau _{2}{text{ or }}tau _{2}subseteq tau {text{ then }}tau =tau _{2}}$ ). Por ejemplo, si ${displaystyle (X,p){text{ and }}(X,q)}$ son espacios de Banach con topologías ${displaystyle tau _{p}{text{ and }}tau _{q}}$ y si uno de estos espacios tiene una bola abierta que también es un subconjunto abierto del otro espacio (o equivalentemente, si uno de ellos ${displaystyle p:left(X,tau _{q}right)to mathbb {R} }$ o ${displaystyle q:left(X,tau _{p}right)to mathbb {R} }$ es continua) entonces sus topologías son idénticas y sus normas son equivalentes.

Integridad

Normas completas y normas equivalentes

Dos normas, $p$ y $q,$ en un espacio vectorial se dice que equivalente si inducen la misma topología; esto sucede si y sólo si existen números reales positivos $0}" xmlns="http://www.w3.org/1998/Math/MathML">c,C■0{displaystyle c,C confía0}0}" aria-hidden="true" class="mwe-math-fallback-image-inline" src="https://wikimedia.org/api/rest_v1/media/math/render/svg/162c3821972f14a29ea8156f42fda96fac3822d7" style="vertical-align: -0.671ex; width:8.068ex; height:2.509ex;"/>$ tales que ${textstyle cq(x)leq p(x)leq Cq(x)}$ para todos ${displaystyle xin X.}$ Si $p$ y $q$ son dos normas equivalentes en un espacio vectorial $X$ entonces ${displaystyle (X,p)}$ es un espacio de Banach si y sólo si ${displaystyle (X,q)}$ es un espacio de Banach. Vea esta nota de pie de página para un ejemplo de una norma continua en un espacio de Banach que es no equivalente a la norma dada del espacio de Banach. Todas las normas sobre un espacio vectorial de dimensiones finitas son equivalentes y cada espacio de dimensiones finitas es un espacio de Banach.

Normas completas frente a métricas completas

Una métrica $D$ en un espacio vectorial $X$ es inducido por una norma en $X$ si $D$ es traducción invariante y absolutamente homogénea, lo que significa que ${displaystyle D(sx,sy)=|s|D(x,y)}$ para todos los escalares $s$ y todos ${displaystyle x,yin X,}$ en cuyo caso la función ${displaystyle |x|:=D(x,0)}$ define una norma en $X$ y la métrica canónica inducida por $|cdot |$ es igual a $D.$

Supongamos que $(X, |cdot|)$ es un espacio normal y que $tau$ es la topología de la norma inducida $X.$ Supongamos que $D$ es cualquiera métricas $X$ tal que la topología que $D$ induce a $X$ es igual a $tau.$ Si $D$ es traducción invariable entonces $(X, |cdot|)$ es un espacio de Banach si y sólo si ${displaystyle (X,D)}$ es un espacio métrico completo. Si $D$ es no traducción invariable, entonces puede ser posible $(X, |cdot|)$ ser un espacio de Banach pero para ${displaystyle (X,D)}$ a no ser un espacio métrico completo (ver esta nota de pie de página por ejemplo). En cambio, un teorema de Klee, que también se aplica a todos los espacios topológicos metrizables vectoriales, implica que si existe cualquiera métrica completa $D$ on $X$ que induce la topología de la norma $tau$ on $X,$ entonces $(X, |cdot|)$ es un espacio de Banach.

Un espacio Fréchet es un espacio vectorial topológico localmente convexo cuya topología es inducida por alguna métrica completa de traducción-invariante. Cada espacio de Banach es un espacio Fréchet pero no transversalmente; de hecho, incluso existen espacios Fréchet en los que ninguna norma es una función continua (como el espacio de secuencias reales) ${textstyle mathbb {R} ^{mathbb {N} }=prod _{iin mathbb {N} }mathbb {R} }$ con la topología del producto). Sin embargo, la topología de cada espacio Fréchet es inducida por algunas familias contables de mapas reales (necesariamente continuos) llamados seminormas, que son generalizaciones de normas. Incluso es posible que un espacio Fréchet tenga una topología inducida por una familia contable normas (Estas normas serían necesariamente continuas) pero no ser un espacio banach/normable porque su topología no puede ser definida por ninguna single norma. Un ejemplo de tal espacio es el espacio Fréchet ${displaystyle C^{infty }(K),}$ cuya definición se puede encontrar en el artículo sobre espacios de funciones y distribuciones de prueba.

Normas completas frente a espacios vectoriales topológicos completos

Hay otra noción de integridad además de la integridad métrica y que es la noción de un espacio vectorial topológico completo (TVS) o la complete TVS, que utiliza la teoría de los espacios uniformes. Específicamente, la noción de la complete TVS utiliza una uniformidad única de traducción-invariante, llamada la uniformidad canónica, que depende sólo en la tracción vectorial y la topología $tau$ que el espacio vectorial está dotado, y por lo tanto en particular, esta noción de la integridad TVS es independiente de cualquier norma inducida la topología $tau$ (e incluso se aplica a los TVS que son no incluso metrizable). Cada espacio de Banach es un TVS completo. Además, un espacio normalizado es un espacio de Banach (es decir, su métrica inducida por la norma está completa) si y sólo si está completo como un espacio vectorial topológico. Si $(X, tau)$ es un espacio vectorial topológico metrizable (como cualquier topología inducida por norma, por ejemplo), entonces $(X, tau)$ es un TVS completo si y sólo si es un secuencial TVS completo, lo que significa que es suficiente para comprobar que Cauchy secuencia dentro $(X, tau)$ convergencias en $(X, tau)$ a algún punto $X$ (es decir, no hay necesidad de considerar la noción más general de redes Cauchy arbitrarias).

Si $(X, tau)$ es un espacio vectorial topológico cuya topología es inducida por algunos (posiblemente desconocido) norma (se llaman tales espacios) normable y se caracterizan por ser Hausdorff y tener un barrio convexo vinculado del origen), entonces $(X, tau)$ es un espacio vectorial topológico completo si y sólo si $X$ puede ser asignado una norma $|cdot |$ que induce $X$ la topología $tau$ y también hace $(X, |cdot|)$ en un espacio de Banach. Un espacio vectorial topológico de Hausdorff localmente $X$ es normable si y sólo si su espacio dual fuerte ${displaystyle X_{b}^{prime }}$ es normable, en cuyo caso ${displaystyle X_{b}^{prime }}$ es un espacio de Banach ( ${displaystyle X_{b}^{prime }}$ denota el espacio dual fuerte $X,$ cuya topología es una generalización de la topología inducida por la doble norma en el espacio dual continuo ${displaystyle X^{prime }}$ ; vea esta nota para más detalles). Si $X$ es un metroble localmente convex TVS, entonces $X$ es normable si y sólo si ${displaystyle X_{b}^{prime }}$ es un espacio Fréchet-Urysohn. Esto demuestra que en la categoría de TVSs locales convexos, los espacios de Banach son exactamente los espacios completos que son tanto metrizables y tienen espacios duales fuertes y metrizables.

Terminaciones

Todo espacio normado se puede incrustar isométricamente en un subespacio vectorial denso de algún espacio de Banach, donde este espacio de Banach se denomina complemento del espacio normado. Esta terminación de Hausdorff es única hasta el isomorfismo isométrico.

Más precisamente, por cada espacio normal $X,$ hay un espacio de Banach $Y$ y una cartografía ${displaystyle T:Xto Y}$ tales que $T$ es una cartografía isométrica y $T(X)$ es denso en $Y.$ Si $Z$ es otro espacio de Banach tal que hay un isométrico isomorfismo de $X$ sobre un subconjunto denso $Z,$ entonces $Z$ es isométricamente isomorfo a $Y.$ Este espacio de Banach $Y$ es la terminación Hausdorff del espacio normal $X.$ El espacio métrico subyacente $Y$ es el mismo que la terminación métrica $X,$ con las operaciones espaciales vectoriales $X$ a $Y.$ The completion of $X$ a veces se denota ${displaystyle {widehat {X}}.}$

Teoría general

Operadores lineales, isomorfismos

Si $X$ y $Y$ son espacios ordenados sobre el mismo terreno ${displaystyle mathbb {K}}$ el conjunto de todo continuo $mathbb {K}$ - mapas lineales ${displaystyle T:Xto Y}$ es denotado por ${displaystyle B(X,Y).}$ En espacios infinitos, no todos los mapas lineales son continuos. Una cartografía lineal de un espacio normal $X$ a otro espacio normal es continuo si y sólo si está atado en la bola de unidad cerrada $X.$ Así, el espacio vectorial ${displaystyle B(X,Y)}$ se puede dar la norma del operador

{displaystyle |T|=sup left{|Tx|_{Y}mid xin X, |x|_{X}leq 1right}.}

Para $Y$ un espacio de Banach, el espacio ${displaystyle B(X,Y)}$ es un espacio de Banach con respecto a esta norma. En contextos categóricos, a veces es conveniente restringir el espacio de función entre dos espacios de Banach a sólo los mapas cortos; en ese caso el espacio ${displaystyle B(X,Y)}$ reaparece como bifunctor natural.

Si $X$ es un espacio de Banach, el espacio ${displaystyle B(X)=B(X,X)}$ forma un álgebra de Banach unitaria; la operación de multiplicación es dada por la composición de mapas lineales.

Si $X$ y $Y$ son espacios ordenados, son espacios naturales si existe una bijeción lineal ${displaystyle T:Xto Y}$ tales que $T$ y su inverso $T^{-1}$ son continuos. Si uno de los dos espacios $X$ o $Y$ es completo (o reflexivo, separable, etc.) entonces también es el otro espacio. Dos espacios no autorizados $X$ y $Y$ son isométricamente isomorfo si además, $T$ es una isometría, es decir, ${displaystyle |T(x)|=|x|}$ para todos $x$ dentro $X.$ La distancia de Banach-Mazur $d(X, Y)$ entre dos espacios isomorfos pero no isométricos $X$ y $Y$ da una medida de cuánto los dos espacios $X$ y $Y$ difieren.

Funciones lineales continuas y acotadas y seminormas

Cada operador lineal continuo es un operador lineal atado y si trata sólo con espacios ordenados entonces el converso es también cierto. Es decir, un operador lineal entre dos espacios normalizados está atado si y sólo si es una función continua. Así en particular, porque el campo de escalar (que es $mathbb {R}$ o $mathbb{C}$ ) es un espacio normal, un funcional lineal en un espacio normal es un funcional lineal ligado si y sólo si es un funcional lineal continuo. Esto permite que los resultados relacionados con la continuidad (como los siguientes) se apliquen a los espacios de Banach. Aunque la contención es la misma que la continuidad de los mapas lineales entre espacios ordenados, el término "abundado" es más comúnmente utilizado cuando se trata principalmente de los espacios de Banach.

Si ${displaystyle f:Xto mathbb {R} }$ es una función subadditiva (como una norma, una función sublinear, o real funcional lineal), entonces $f$ es continuo en el origen si y sólo si $f$ es uniformemente continuo en todo $X$ ; y si además $f(0)=0$ entonces $f$ es continuo si y sólo si su valor absoluto ${displaystyle |f|:Xto [0,infty)}$ es continuo, que sucede si y sólo si $<math alttext="{displaystyle {xin X:|f(x)|{}x▪ ▪ X:Silenciof()x)Silencio.1}{displaystyle {xin X: preservef(x) <img alt="{displaystyle {xin X:|f(x)|$ es un subconjunto abierto de $X.$ Y muy importante para aplicar el teorema Hahn-Banach, un funcional lineal $f$ es continuo si y sólo si esto es verdad de su parte real ${displaystyle operatorname {Re} f}$ y, además, ${displaystyle |operatorname {Re} f|=|f|}$ y la parte real ${displaystyle operatorname {Re} f}$ determina completamente $f,$ por lo que el teorema Hahn-Banach se declara a menudo sólo para las funciones lineales reales. Además, un funcional lineal $f$ on $X$ es continuo si y sólo si el seminorm $|f|$ es continuo, que sucede si y sólo si existe un seminorm continuo ${displaystyle p:Xto mathbb {R} }$ tales que ${displaystyle |f|leq p}$ ; esta última declaración que implica el funcionamiento lineal $f$ y seminorm $p$ se encuentra en muchas versiones del teorema Hahn-Banach.

Nociones básicas

El producto cartesiano $Xtimes Y$ de dos espacios ordenados no está canónicamente equipado con una norma. Sin embargo, varias normas equivalentes se utilizan comúnmente, como

{displaystyle |(x,y)|_{1}=|x|+|y|,qquad |(x,y)|_{infty }=max(|x|,|y|)}

Xtimes Y

{displaystyle Xoplus Y}

Si $M$ es un subespacio lineal cerrado de un espacio normal $X,$ hay una norma natural en espacio de referencia ${displaystyle X/M,}$

{displaystyle |x+M|=inf limits _{min M}|x+m|.}

El cociente ${displaystyle X/M}$ es un espacio de Banach cuando $X$ está completo. El mapa de referencia desde $X$ sobre ${displaystyle X/M,}$ envío $xin X$ a su clase ${displaystyle x+M,}$ es lineal, y tiene norma $1,$ excepto cuando ${displaystyle M=X,}$ en cuyo caso el cociente es el espacio nulo.

El subespacio lineal cerrado $M$ de $X$ se dice que es un subespacial complementario de $X$ si $M$ es el rango de una proyección lineal ligada surjetiva ${displaystyle P:Xto M.}$ En este caso, el espacio $X$ es isomorfo a la suma directa $M$ y ${displaystyle ker P,}$ el núcleo de la proyección $P.$

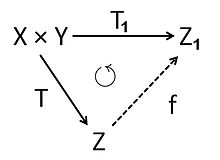
Supongamos que $X$ y $Y$ son espacios de Banach y que ${displaystyle Tin B(X,Y).}$ Existe una factorización canónica de $T$ como

{displaystyle T=T_{1}circ pi T:X {overset {pi }{longrightarrow }} X/ker(T) {overset {T_{1}}{longrightarrow }} Y}

pi

T_{1}

{displaystyle x+ker T}

T(x)

{displaystyle Y.,}

T_{1}

{displaystyle X/ker T}

{displaystyle T(X),}

Espacios clásicos

Ejemplos básicos de espacios de Banach incluyen: los espacios Lp $L^{p}$ y sus casos especiales, los espacios de secuencia $ell ^{p}$ que consiste en secuencias escalar indexadas por números naturales $mathbb {N}$ ; entre ellos, el espacio $ell ^{1}$ de secuencias absolutamente sumibles y el espacio $ell ^{2}$ de secuencias cuadradas sumergibles; el espacio $c_{0}$ de secuencias que tienden a cero y el espacio ${displaystyle ell ^{infty }}$ de secuencias atadas; el espacio $C(K)$ de funciones de escalar continuas en un espacio Hausdorff compacto $K,$ equipado con la norma máxima,

{displaystyle |f|_{C(K)}=max{|f(x)|:xin K},quad fin C(K).}

Según el teorema de Banach-Mazur, cada espacio de Banach es isométricamente isomorfo a un subespacio de algunos ${displaystyle C(K).}$ Para cada espacio separado de Banach $X,$ hay un subespacial cerrado $M$ de $ell ^{1}$ tales que ${displaystyle X:=ell ^{1}/M.}$

Cualquier espacio de Hilbert sirve como ejemplo de un espacio de Banach. Un espacio de Hilbert $H$ on ${displaystyle mathbb {K} =mathbb {R}mathbb {C} }$ es completo para una norma de la forma

{displaystyle |x|_{H}={sqrt {langle x,xrangle }},}

{displaystyle langle cdotcdot rangle:Htimes Hto mathbb {K} }

{displaystyle {begin{aligned}langle y,xrangle &={overline {langle x,yrangle }},quad {text{ for all }}x,yin H\langle x,xrangle &geq 0,quad {text{ for all }}xin H\langle x,xrangle =0{text{ if and only if }}x&=0.end{aligned}}}

Por ejemplo, el espacio $L^{2}$ es un espacio de Hilbert.

Los espacios Hardy, los espacios Sobolev son ejemplos de espacios de Banach que están relacionados con $L^{p}$ espacios y tienen estructura adicional. Son importantes en diferentes ramas de análisis, análisis armónico y ecuaciones diferenciales parciales entre otros.

Álgebras de Banach

A Banach álgebra es un espacio de Banach $A$ sobre ${displaystyle mathbb {K} =mathbb {R} }$ o ${displaystyle mathbb {C}}$ junto con una estructura de álgebra sobre $mathbb {K}$ , tal que el mapa del producto ${displaystyle Atimes Ani (a,b)mapsto abin A}$ es continuo. Una norma equivalente $A$ se puede encontrar para que ${displaystyle |ab|leq |a||b|}$ para todos ${displaystyle a,bin A.}$

Ejemplos

El espacio de Banach $C(K)$ con el producto de punta, es un álgebra de Banach.
El álgebra del disco ${displaystyle A(mathbf {D})}$ consiste en funciones holomorfas en el disco de unidad abierta ${displaystyle Dsubseteq mathbb {C} }$ y continua en su cierre: ${displaystyle {overline {mathbf {D} }}.}$ Equipado con la norma máxima en ${displaystyle {overline {mathbf {D} }},}$ el álgebra del disco ${displaystyle A(mathbf {D})}$ es un subalgebra cerrado ${displaystyle Cleft({overline {mathbf {D} }}right).}$
El álgebra de Wiener ${displaystyle A(mathbf {T})}$ es el álgebra de las funciones en el círculo de la unidad $mathbf {T}$ con la serie Fourier absolutamente convergente. Via the map associating a function on $mathbf {T}$ a la secuencia de sus coeficientes Fourier, este álgebra es isomorfo al álgebra de Banach ${displaystyle ell ^{1}(Z),}$ donde el producto es la evolución de las secuencias.
Por cada espacio de Banach $X,$ el espacio ${displaystyle B(X)}$ of bounded linear operators on $X,$ con la composición de mapas como producto, es un álgebra de Banach.
A C*-álgebra es un álgebra Banach complejo $A$ con una involución antilinear $amapsto a^{*}$ tales que ${displaystyle left|a^{*}aright|=|a|^{2}.}$ El espacio $B(H)$ de operadores lineales en un espacio Hilbert $H$ es un ejemplo fundamental de C*-álgebra. El teorema Gelfand–Naimark afirma que cada álgebra C* es isométricamente isomorfa a un subálgebra C* de algunos ${displaystyle B(H).}$ El espacio $C(K)$ de complejas funciones continuas en un espacio compacto Hausdorff $K$ es un ejemplo de C*-álgebra conmutativa, donde la involución asocia a cada función $f$ su complejo conjugado ${displaystyle {overline {f}}.}$

Doble espacio

Si $X$ es un espacio normal y $mathbb {K}$ el campo subyacente (ya sean los números reales o complejos), el espacio dual continuo es el espacio de mapas lineales continuos de $X$ en ${displaystyle mathbb {K}}$ o funcionales lineales continuos. La notación para el dual continuo es ${displaystyle X^{prime }=B(X,mathbb {K})}$ en este artículo. Desde $mathbb {K}$ es un espacio de Banach (utilizando el valor absoluto como norma), el dual ${displaystyle X^{prime }}$ es un espacio de Banach, para cada espacio normal $X.$

La principal herramienta para demostrar la existencia de funcionales lineales continuos es el teorema de Hahn-Banach.

Teorema de Hahn-Banach—Vamos $X$ ser un espacio vectorial sobre el terreno ${displaystyle mathbb {K} =mathbb {R}mathbb {C}.}$ Let further

$Y subseteq X$ ser un subespacio lineal,
${displaystyle p:Xto mathbb {R} }$ ser una función sublinear y
${displaystyle f:Yto mathbb {K} }$ ser un funcional lineal para que ${displaystyle operatorname {Re} (f(y))leq p(y)}$ para todos ${displaystyle yin Y.}$

Entonces, existe un funcional lineal ${displaystyle F:Xto mathbb {K} }$ así

{displaystyle F{big vert }_{Y}=f,quad {text{ and }}quad {text{ for all }}xin X, operatorname {Re} (F(x))leq p(x).}

En particular, todas las funciones lineales continuas en un subespacio de un espacio normal pueden extenderse continuamente a todo el espacio, sin aumentar la norma de lo funcional. Un caso especial importante es el siguiente: para cada vector $x$ en un espacio normal $X,$ existe un funcionamiento lineal continuo $f$ on $X$ tales que

{displaystyle f(x)=|x|_{X},quad |f|_{X^{prime }}leq 1.}

Cuando $x$ no es igual a la $mathbf {0}$ vector, el funcional $f$ debe tener una norma, y se llama funcional para $x.$

El teorema de separación de Hahn-Banach establece que dos conjuntos convexos no vacíos disjuntos en un espacio de Banach real, uno de ellos abierto, pueden estar separados por un hiperplano afín cerrado. El conjunto convexo abierto se encuentra estrictamente en un lado del hiperplano, el segundo conjunto convexo se encuentra en el otro lado pero puede tocar el hiperplano.

Un subconjunto $S$ en un espacio de Banach $X$ es total si el lazo lineal $S$ es denso en $X.$ El subconjunto $S$ total $X$ si y sólo si el único funcionamiento lineal continuo que desaparece $S$ es $mathbf {0}$ funcional: esta equivalencia se deriva del teorema Hahn-Banach.

Si $X$ es la suma directa de dos subespacios lineales cerrados $M$ y $N,$ entonces el dual ${displaystyle X^{prime }}$ de $X$ es isomorfo a la suma directa de los duales de $M$ y ${displaystyle N.}$ Si $M$ es un subespacio lineal cerrado en $X,$ uno puede asociar el ortogonal of $M$ en el doble,

{displaystyle M^{bot}=left{x^{prime }in X:x^{prime }(m)=0, {text{ for all }}min Mright}.}

La ortogonal ${displaystyle M^{bot }}$ es un subespacio lineal cerrado del dual. La dualidad de $M$ es isométricamente isomorfo a ${displaystyle X'/M^{bot }.}$ El doble de ${displaystyle X/M}$ es isométricamente isomorfo a ${displaystyle M^{bot }.}$

El dual de un espacio de Banach separable no necesita ser separable, pero:

Theorem—Vamos $X$ ser un espacio normal. Si $X'$ es separable, entonces $X$ es separable.

Cuando $X'$ es separable, el criterio anterior para la totalidad se puede utilizar para probar la existencia de un subconjunto total contable en $X.$

Topologías débiles

El débil topología sobre un espacio de Banach $X$ es la topología más gruesa en $X$ para los cuales todos los elementos ${displaystyle x^{prime }}$ en el espacio dual continuo ${displaystyle X^{prime }}$ son continuos. La topología de la norma es más fina que la topología débil. A continuación del teorema de separación Hahn-Banach que la topología débil es Hausdorff, y que un subconjunto convexo cerrado de norma de un espacio de Banach también está débilmente cerrado. Un mapa lineal de norma continua entre dos espacios de Banach $X$ y $Y$ también débilmente continuo, es decir, continuo de la débil topología de $X$ a la $Y.$

Si $X$ es infinita-dimensional, existen mapas lineales que no son continuos. El espacio $X^{*}$ de todos los mapas lineales de $X$ en la esfera subyacente $mathbb {K}$ (este espacio $X^{*}$ se llama el espacio dual algebraico, para distinguirlo de ${displaystyle X^{prime }}$ también induce una topología en $X$ que es más fino que la topología débil, y mucho menos utilizado en el análisis funcional.

En un espacio dual ${displaystyle X^{prime },}$ hay una topología más débil que la débil topología ${displaystyle X^{prime },}$ llamada débil* topología. Es la topología más gruesa. ${displaystyle X^{prime }}$ para los cuales todos los mapas de evaluación ${displaystyle x^{prime }in X^{prime }mapsto x^{prime }(x),}$ Donde $x$ rangos sobre $X,$ son continuos. Su importancia proviene del teorema Banach-Alaoglu.

Banach-Alaoglu theorem—Vamos $X$ ser un espacio vectorial normal. Luego la bola de unidad cerrada ${displaystyle B=left{xin X:|x|leq 1right}}$ del espacio dual es compacto en la topología débil*.

El teorema de Banach-Alaoglu puede probarse usando el teorema de Tychonoff sobre productos infinitos de espacios compactos de Hausdorff. Cuando $X$ es separable, la bola unidad $B^{{prime }}$ de la dual es un compacto metroble en la topología débil*.

Ejemplos de espacios duales

El doble de $c_{0}$ es isométricamente isomorfo a $ell ^{1}$ : para cada funcional lineal ligado $f$ on ${displaystyle c_{0},}$ hay un elemento único ${displaystyle y=left{y_{n}right}in ell ^{1}}$ tales que

{displaystyle f(x)=sum _{nin mathbb {N} }x_{n}y_{n},qquad x={x_{n}}in c_{0}, {text{and}} |f|_{(c_{0})'}=|y|_{ell _{1}}.}

El doble de $ell ^{1}$ es isométricamente isomorfo a ${displaystyle ell ^{infty }}$ . El doble espacio de Lebesgue ${displaystyle L^{p}([0,1])}$ es isométricamente isomorfo a ${displaystyle L^{q}([0,1])}$ cuando $<math alttext="{displaystyle 1leq p1\leq \leq p.JUEGO JUEGO {displaystyle 1leq p buscadoinfty} <img alt="1 leq p$ y ${displaystyle {frac {1}{p}}+{frac {1}{q}}=1.}$

Por cada vector $y$ en un espacio Hilbert $H,$ la asignación

{displaystyle xin Hto f_{y}(x)=langle x,yrangle }

define un funcionamiento lineal continuo $f_y$ on $H.$ El teorema de representación Riesz establece que cada funcional lineal continuo en $H$ es de la forma $f_y$ para un vector único $y$ dentro $H.$ La asignación ${displaystyle yin Hto f_{y}}$ es una bijeción isométrica antilinear $H$ sobre su doble ${displaystyle H'.}$ Cuando los escalares son reales, este mapa es un isométrico isomorfismo.

Cuando $K$ es un espacio topológico compacto Hausdorff, el doble ${displaystyle M(K)}$ de $C(K)$ es el espacio de las medidas de Radon en el sentido de Bourbaki. El subconjunto ${displaystyle P(K)}$ de ${displaystyle M(K)}$ consistente en medidas no negativas de masa 1 (medidas de probabilidad) es un subconvexo w* cerrado de la bola unitaria de la ${displaystyle M(K).}$ Los puntos extremos ${displaystyle P(K)}$ son las medidas Dirac sobre $K.$ El conjunto de medidas Dirac sobre $K,$ equipado con la w*-topología, es homeomorfa a $K.$

Banach-Stone Theorem—Si $K$ y $L$ son espacios compactos Hausdorff y si $C(K)$ y ${displaystyle C(L)}$ son isométricamente isomorfos, luego los espacios topológicos $K$ y $L$ son homeomorfos.

El resultado ha sido extendido por Amir y Cambern al caso cuando la distancia multiplicativa Banach-Mazur entre $C(K)$ y ${displaystyle C(L)}$ es $<math alttext="{displaystyle .2.{displaystyle. <img alt="{displaystyle$ El teorema ya no es cierto cuando la distancia es ${displaystyle =2.}$

En el álgebra de Banach Comutativo ${displaystyle C(K),}$ los ideales máximos son precisamente los núcleos de medidas Dirac en $K,$

{displaystyle I_{x}=ker delta _{x}={fin C(K):f(x)=0},quad xin K.}

Más generalmente, por el teorema de Gelfand-Mazur, los ideales máximos de un álgebra de Banach unitaria pueden identificarse con sus personajes, no sólo como conjuntos sino como espacios topológicos: el primero con la topología del casco y el último con la w*-topología. En esta identificación, el espacio ideal máximo se puede ver como un subconjunto w*-compacto de la bola unitaria en el doble ${displaystyle A'.}$

Theorem—Si $K$ es un espacio Hausdorff compacto, luego el espacio ideal maximal $Xi$ del álgebra de Banach $C(K)$ es homeomorfo a $K.$

No cada álgebra de Banach unitaria es de la forma $C(K)$ para un espacio compacto Hausdorff $K.$ Sin embargo, esta declaración sostiene si uno de los lugares $C(K)$ en la categoría más pequeña de álgebras C* conmutativa. Gelfand's representation theorem for commutative C*-algebras states that every commutative unital C*-algebra $A$ es isométricamente isomorfo a $C(K)$ espacio. El espacio compacto Hausdorff $K$ aquí es de nuevo el espacio ideal maximal, también llamado el espectro de $A$ en el contexto C*-álgebra.

Bidual

Si $X$ es un espacio normal, el doble (continua) $X''$ de la dualidad $X'$ se llama licitación, o segundo doble de $X.$ Por cada espacio normal $X,$ hay un mapa natural,

{displaystyle {begin{cases}F_{X}:Xto X''\F_{X}(x)(f)=f(x)&{text{ for all }}xin X,{text{ and for all }}fin X'end{cases}}}

Esto define $F_X(x)$ como un funcionamiento lineal continuo en ${displaystyle X^{prime },}$ es decir, un elemento ${displaystyle X^{prime prime }.}$ El mapa ${displaystyle F_{X}:xto F_{X}(x)}$ es un mapa lineal desde $X$ a ${displaystyle X^{prime prime }.}$ Como consecuencia de la existencia de una norma funcional $f$ para todos ${displaystyle xin X,}$ este mapa $F_{X}$ es isométrico, por lo tanto inyectable.

Por ejemplo, el doble ${displaystyle X=c_{0}}$ se identifica con ${displaystyle ell ^{1},}$ y el doble $ell ^{1}$ se identifica con ${displaystyle ell ^{infty },}$ el espacio de secuencias de escalar enlazadas. Bajo estas identificaciones, $F_{X}$ es el mapa de inclusión desde $c_{0}$ a ${displaystyle ell ^{infty }.}$ Es realmente isométrico, pero no sobre.

Si $F_{X}$ es subjetivo, entonces el espacio normal $X$ se llama reflexivo (véase infra). Ser el doble de un espacio normal, el bidual $X''$ es completo, por lo tanto, todo espacio reflexivo y nominado es un espacio de Banach.

Usando la incrustación isométrica ${displaystyle F_{X},}$ es habitual considerar un espacio normal $X$ como subconjunto de su bidual. Cuando $X$ es un espacio de Banach, se ve como un subespacio lineal cerrado ${displaystyle X^{prime prime }.}$ Si $X$ no es reflexivo, la bola de unidad de $X$ es un subconjunto adecuado de la bola de unidad de ${displaystyle X^{prime prime }.}$ El teorema de Goldstine establece que la bola unitaria de un espacio normal es débilmente*-denso en la bola unitaria del bidual. En otras palabras, para cada $x''$ en el bidual, existe una red ${displaystyle left(x_{i}right)_{iin I}}$ dentro $X$ así

{displaystyle sup _{iin I}left|x_{i}right|leq |x''|, x''(f)=lim _{i}fleft(x_{i}right),quad fin X'.}

La red puede ser reemplazada por una secuencia débil*-convergente cuando la doble $X'$ es separable. Por otra parte, elementos del bidual $ell ^{1}$ que no están $ell ^{1}$ no puede ser débil* secuencias dentro ${displaystyle ell ^{1},}$ desde entonces $ell ^{1}$ es débilmente secuencialmente completo.

Teoremas de Banach

Aquí están los principales resultados generales sobre los espacios de Banach que se remontan a la época del libro de Banach (Banach (1932)) y están relacionados con el teorema de la categoría de Baire. De acuerdo con este teorema, un espacio métrico completo (como un espacio de Banach, un espacio de Fréchet o un espacio F) no puede ser igual a una unión de muchos subconjuntos cerrados numerables con interiores vacíos. Por lo tanto, un espacio de Banach no puede ser la unión de muchos subespacios cerrados numerables, a menos que ya sea igual a uno de ellos; un espacio de Banach con una base de Hamel numerable es de dimensión finita.

Banach-Steinhaus Theorem—Vamos $X$ ser un espacio de Banach y $Y$ ser un espacio vectorial normal. Supongamos que $F$ es una colección de operadores lineales continuos de $X$ a $Y.$ El principio de uniformidad establece que si para todos $x$ dentro $X$ tenemos $<math alttext="{displaystyle sup _{Tin F}|T(x)|_{Y}SupT▪ ▪ F.. T()x).. Y.JUEGO JUEGO ,{displaystyle sup _{Tin F}fnciónT(x)fnción_{Y}]<img alt="{displaystyle sup _{Tin F}|T(x)|_{Y}$ entonces $<math alttext="{displaystyle sup _{Tin F}|T|_{Y}SupT▪ ▪ F.. T.. Y.JUEGO JUEGO .{displaystyle sup _{Tin F}fnciónTfnción_{Y}Seleccionadoinfty.}<img alt="{displaystyle sup _{Tin F}|T|_{Y}$

El teorema de Banach-Steinhaus no se limita a los espacios de Banach. Puede extenderse por ejemplo al caso en que $X$ es un espacio Fréchet, siempre que la conclusión se modifique como sigue: bajo la misma hipótesis, existe un barrio $U$ de $mathbf {0}$ dentro $X$ tal que todo $T$ dentro $F$ están unidos uniformemente ${displaystyle U,}$

<math alttext="{displaystyle sup _{Tin F}sup _{xin U};|T(x)|_{Y}SupT▪ ▪ FSupx▪ ▪ U.. T()x).. Y.JUEGO JUEGO .{displaystyle sup ¿Por qué?<img alt="{displaystyle sup _{Tin F}sup _{xin U};|T(x)|_{Y}

The Open Mapping Theorem—Vamos $X$ y $Y$ ser espacios y ${displaystyle T:Xto Y}$ ser un operador lineal continuo subjetivo, entonces $T$ es un mapa abierto.

Corollary—Cada operador lineal unido de un espacio de Banach en un espacio de Banach es un isomorfismo.

The First Isomorphism Theorem for Banach space—Supongamos que $X$ y $Y$ son espacios de Banach y que ${displaystyle Tin B(X,Y).}$ Supongamos además que la gama de $T$ está cerrado $Y.$ Entonces... ${displaystyle X/ker T}$ es isomorfo a ${displaystyle T(X).}$

Este resultado es una consecuencia directa del anterior teorema de isomorfismo de Banach y de la factorización canónica de mapas lineales acotados.

Corollary—Si un espacio de Banach $X$ es la suma interna directa de subespacios cerrados ${displaystyle M_{1},ldotsM_{n},}$ entonces $X$ es isomorfo a ${displaystyle M_{1}oplus cdots oplus M_{n}.}$

Esta es otra consecuencia del teorema de isomorfismo de Banach, aplicado a la bijección continua de ${displaystyle M_{1}oplus cdots oplus M_{n}}$ sobre $X$ envío ${displaystyle m_{1},cdotsm_{n}}$ a la suma ${displaystyle m_{1}+cdots +m_{n}.}$

El Teorema de Gráficos Cerrados—Vamos ${displaystyle T:Xto Y}$ ser un mapeo lineal entre los espacios de Banach. El gráfico de $T$ está cerrado $Xtimes Y$ si $T$ es continuo.

Reflexividad

El espacio normal $X$ se llama reflexivo cuando el mapa natural

{displaystyle {begin{cases}F_{X}:Xto X''\F_{X}(x)(f)=f(x)&{text{ for all }}xin X,{text{ and for all }}fin X'end{cases}}}

Theorem—Si $X$ es un espacio de Banach reflexivo, cada subespacio cerrado $X$ y cada espacio conveniente $X$ son reflexivos.

Esta es una consecuencia del teorema Hahn-Banach. Además, por el teorema de mapeo abierto, si hay un operador lineal vinculado del espacio de Banach $X$ sobre el espacio de Banach $Y,$ entonces $Y$ es reflexivo.

Theorem—Si $X$ es un espacio de Banach, entonces $X$ es reflexivo si y sólo si ${displaystyle X^{prime }}$ es reflexivo.

Corollary—Vamos $X$ ser un espacio de Banach reflexivo. Entonces... $X$ es separable si y sólo si ${displaystyle X^{prime }}$ es separable.

De hecho, si el dual ${displaystyle Y^{prime }}$ de un espacio de Banach $Y$ es separable, entonces $Y$ es separable. Si $X$ es reflexivo y separable, entonces el dual de ${displaystyle X^{prime }}$ es separable, así que ${displaystyle X^{prime }}$ es separable.

Theorem—Supongamos que $X_1, ldots, X_n$ son espacios ordenados y que ${displaystyle X=X_{1}oplus cdots oplus X_{n}.}$ Entonces... $X$ es reflexivo si y sólo si cada uno $X_{j}$ es reflexivo.

Los espacios de Hilbert son reflexivos. El $L^{p}$ los espacios son reflexivos cuando $<math alttext="{displaystyle 1<p1.p.JUEGO JUEGO .{displaystyle 1 seccionóinfty.} <img alt="{displaystyle 1<p$ Más generalmente, los espacios convexos uniformemente son reflexivos, por el teorema Milman-Pettis. Los espacios ${displaystyle c_{0},ell ^{1},L^{1}([0,1]),C([0,1])}$ no son reflexivos. En estos ejemplos de espacios no reflexivos $X,$ la licitación $X''$ es "mucho más grande" que $X.$ Es decir, bajo la incrustación isométrica natural $X$ en $X''$ dado por el teorema Hahn-Banach, el cociente ${displaystyle X^{prime prime }/X}$ es infinita-dimensional, e incluso no estable. Sin embargo, Robert C. James ha construido un ejemplo de un espacio no reflexivo, generalmente llamado "el espacio James"y denotado por ${displaystyle J,}$ tal que el cociente ${displaystyle J^{prime prime }/J}$ es una dimensión. Además, este espacio $J$ es isométricamente isomorfo a su bidual.

Theorem—A Banach space $X$ es reflexivo si y sólo si su bola de unidad es compacta en la topología débil.

Cuando $X$ es reflexivo, sigue que todos los subconjuntos convexos cerrados y atados de $X$ son débilmente compactos. En un espacio Hilbert $H,$ la compactidad débil de la bola de unidad se utiliza muy a menudo de la siguiente manera: cada secuencia atada en $H$ tiene subsecuencias débilmente convergentes.

La compactidad débil de la bola unitaria proporciona una herramienta para encontrar soluciones en espacios reflexivos a ciertos problemas de optimización. Por ejemplo, cada función continua convexa en la bola unidad $B$ de un espacio reflexivo alcanza su mínimo en algún momento $B.$

Como caso especial del resultado anterior, cuando $X$ es un espacio reflexivo sobre ${displaystyle mathbb {R}}$ cada funcional lineal continuo $f$ dentro ${displaystyle X^{prime }}$ alcanza su máximo ${displaystyle |f|}$ en la bola de unidad $X.$ El siguiente teorema de Robert C. James proporciona una declaración inversa.

Teorema de James—Para un espacio de Banach las dos propiedades siguientes son equivalentes:

$X$ es reflexivo.
para todos $f$ dentro ${displaystyle X^{prime }}$ existe $xin X$ con ${displaystyle |x|leq 1,}$ así ${displaystyle f(x)=|f|.}$

El teorema se puede extender para dar una caracterización de conjuntos convexos débilmente compactos.

En cada espacio de Banach no reflexivo $X,$ existen funciones lineales continuas que no son que contiene normas. Sin embargo, el teorema del Obispo-Phelps afirma que las funciones que contienen la norma son densas en la doble ${displaystyle X^{prime }}$ de $X.$

Débil convergencia de secuencias

Una secuencia ${displaystyle left{x_{n}right}}$ en un espacio de Banach $X$ es débilmente convergente a un vector $xin X$ si ${displaystyle left{fleft(x_{n}right)right}}$ convergencias a $f(x)$ para cada funcional lineal continuo $f$ en el doble ${displaystyle X^{prime }.}$ La secuencia ${displaystyle left{x_{n}right}}$ es un débilmente Cauchy secuencia si ${displaystyle left{fleft(x_{n}right)right}}$ converge a un límite escalar ${displaystyle L(f),,}$ para todos $f$ dentro ${displaystyle X^{prime }.}$ Una secuencia ${displaystyle left{f_{n}right}}$ en el doble ${displaystyle X^{prime }}$ es débil* convergente a un funcional ${displaystyle fin X^{prime }}$ si $f_{n}(x)$ convergencias a $f(x)$ para todos $x$ dentro $X.$ Las secuencias débiles de Cauchy, débilmente convergentes y débilmente* convergentes secuencias están limitadas, como consecuencia del teorema Banach-Steinhaus.

Cuando la secuencia ${displaystyle left{x_{n}right}}$ dentro $X$ es una secuencia débilmente Cauchy, el límite $L$ arriba define un funcional lineal ligado en el dual ${displaystyle X^{prime },}$ es decir, un elemento $L$ of the bidual of $X,$ y $L$ es el límite ${displaystyle left{x_{n}right}}$ en la débil*-topología del bidual. El espacio de Banach $X$ es débilmente secuencialmente completo si cada secuencia débilmente Cauchy es débilmente convergente $X.$ De la discusión anterior se desprende que los espacios reflexivos están débilmente completos secuencialmente.

Theorem —Por cada medida $mu$ el espacio $L^1(mu)$ es débilmente secuencialmente completo.

Una secuencia ortonormal en un espacio de Hilbert es un simple ejemplo de una secuencia débilmente convergente, con límite igual a la $mathbf {0}$ vector. La base vectorial de la unidad $ell ^{p}$ para $<math alttext="{displaystyle 1<p1.p.JUEGO JUEGO ,{displaystyle 1 seccionó] <img alt="{displaystyle 1<p$ o de ${displaystyle c_{0},}$ es otro ejemplo de un secuencia débilmente nula, es decir, una secuencia que converge débilmente ${displaystyle mathbf {0}.}$ Para cada secuencia débilmente nula en un espacio de Banach, existe una secuencia de combinaciones convexas de vectores de la secuencia dada que es normal convergente a ${displaystyle mathbf {0}.}$

La base vectorial de la unidad $ell ^{1}$ no es débilmente Cauchy. Secuencias débilmente Cauchy en $ell ^{1}$ son débilmente convergentes, ya que $L^{1}$ - Los espacios están débiles secuencialmente completos. En realidad, secuencias débilmente convergentes en $ell ^{1}$ son la norma convergente. Esto significa que $ell ^{1}$ Satisface la propiedad de Schur.

Resultados relacionados con la ℓ 1 { estilo de visualización ell ^ {1}} base

Secuencias débilmente Cauchy y las $ell ^{1}$ la base son los casos opuestos de la dicotomía establecida en el siguiente resultado profundo de H. P. Rosenthal.

Theorem—Vamos ${displaystyle left{x_{n}right}_{nin mathbb {N} }}$ ser una secuencia atada en un espacio de Banach. Cualquiera ${displaystyle left{x_{n}right}_{nin mathbb {N} }}$ tiene una subsequencia débil Cauchy, o admite una subsequencia equivalente a la base vectorial de unidad estándar ${displaystyle ell ^{1}.}$

Un complemento a este resultado se debe a Odell y Rosenthal (1975).

Theorem—Vamos $X$ ser un espacio separado de Banach. Los siguientes son equivalentes:

El espacio $X$ no contiene un isomorfo subespacial cerrado ${displaystyle ell ^{1}.}$
Cada elemento del bidual $X''$ es el límite débil* de una secuencia ${displaystyle left{x_{n}right}}$ dentro $X.$

Por el teorema de oro, cada elemento de la bola unidad $B^{{prime prime }}$ de ${displaystyle X^{prime prime }}$ es débil*-limit de una red en la bola unitaria de $X.$ Cuando $X$ no contiene ${displaystyle ell ^{1},}$ cada elemento de $B^{{prime prime }}$ es débil*-limito de un secuencia en la bola de unidad $X.$

Cuando el espacio de Banach $X$ es separable, la bola unitaria del dual ${displaystyle X^{prime },}$ equipado con la débil*-topología, es un espacio compacto $K,$ y todos los elementos ${displaystyle x^{prime prime }}$ en la licitación ${displaystyle X^{prime prime }}$ define una función atada en $K$ :

{displaystyle x'in Kmapsto x''(x'),quad left|x''(x')right|leq left|x''right|.}

Esta función es continua para la topología compacta $K$ si ${displaystyle x^{prime prime }}$ en realidad $X,$ considerado como subconjunto ${displaystyle X^{prime prime }.}$ Asumir además el resto del párrafo que $X$ no contiene ${displaystyle ell ^{1}.}$ Por el resultado anterior de Odell y Rosenthal, la función ${displaystyle x^{prime prime }}$ es el límite de punto en $K$ de una secuencia ${displaystyle left{x_{n}right}subseteq X}$ de funciones continuas $K,$ es por lo tanto una primera función de clase de Baire en $K.$ La bola de unidad del bidual es un subconjunto compacto de punta de la primera clase de Baire en $K.$

Secuencias, compacidad débil y débil*

Cuando $X$ es separable, la bola unitaria de la dual es débil*-compacto por el teorema Banach-Alaoglu y metrizable para la topología débil*, por lo tanto cada secuencia atada en la dual tiene subsecuencias convergentes débilmente*. Esto se aplica a espacios reflexivos separables, pero más es cierto en este caso, como se indica a continuación.

La débil topología de un espacio de Banach $X$ se puede medir si $X$ es finito-dimensional. Si el dual $X'$ es separable, la topología débil de la bola unitaria de $X$ es metro. Esto se aplica en particular a espacios separables de Banach reflexivo. Aunque la topología débil de la bola unitaria no es metrizable en general, se puede caracterizar la compactación débil mediante secuencias.

Eberlein–Teorema Šmuliano—Un juego $A$ en un espacio de Banach es relativamente débilmente compacto si y sólo si cada secuencia ${displaystyle left{a_{n}right}}$ dentro $A$ tiene una subsequencia débilmente convergente.

A Banach space $X$ es reflexivo si y sólo si cada secuencia atada en $X$ tiene una subsequencia débilmente convergente.

Un subconjunto débilmente compacto $A$ dentro $ell ^{1}$ es una norma. De hecho, cada secuencia en $A$ tiene subsecuencias débilmente convergentes por Eberlein-Šmulian, que son norma convergente por la propiedad de Schur ${displaystyle ell ^{1}.}$

Bases Schauder

A Base de Schauder en un espacio de Banach $X$ es una secuencia ${displaystyle left{e_{n}right}_{ngeq 0}}$ de vectores en $X$ con la propiedad que por cada vector ${displaystyle xin X,}$ existe única escalares definidos ${displaystyle left{x_{n}right}_{ngeq 0}}$ dependiendo de $x,$ tales que

{displaystyle x=sum _{n=0}^{infty }x_{n}e_{n},quad {textit {i.e.,}}quad x=lim _{n}P_{n}(x), P_{n}(x):=sum _{k=0}^{n}x_{k}e_{k}.}

Los espacios de Banach con una base de Schauder son necesariamente separables, porque el conjunto contable de combinaciones lineales finitas con coeficientes racionales (digamos) es denso.

De la teorema Banach-Steinhaus se desprende que los mapas lineales ${displaystyle left{P_{n}right}}$ están unidos uniformemente por alguna constante ${displaystyle C.}$ Vamos ${displaystyle left{e_{n}^{*}right}}$ denota las coordenadas funcionales que asignan a cada $x$ dentro $X$ la coordenadas $x_{n}$ de $x$ en la expansión anterior. Se llaman biorthogonales funcionales. Cuando los vectores base tienen norma $1,$ las coordenadas funcionales ${displaystyle left{e_{n}^{*}right}}$ la norma ${displaystyle ,leq 2C}$ en el doble $X.$

La mayoría de los espacios separables clásicos tienen bases explícitas. El sistema Haar ${displaystyle left{h_{n}right}}$ es una base para $<math alttext="{displaystyle L^{p}([0,1]),1leq pLp()[0,1]),1≤ ≤ p.JUEGO JUEGO .{displaystyle L^{p}(0,1]),1leq p buscadoinfty.}<img alt="{displaystyle L^{p}([0,1]),1leq p$ El sistema trigonométrico es una base en ${displaystyle L^{p}(mathbf {T})}$ cuando $<math alttext="{displaystyle 1<p1.p.JUEGO JUEGO .{displaystyle 1 seccionóinfty.} <img alt="{displaystyle 1<p$ El sistema Schauder es una base en el espacio ${displaystyle C([0,1]).}$ La pregunta de si el álgebra del disco ${displaystyle A(mathbf {D})}$ ha permanecido abierta durante más de cuarenta años, hasta que Bočkarev mostró en 1974 que ${displaystyle A(mathbf {D})}$ Admite una base construida del sistema Franklin.

Desde todos los vectores $x$ en un espacio de Banach $X$ con base es el límite ${displaystyle P_{n}(x),}$ con $P_{n}$ de rango finito y unido uniformemente, el espacio $X$ satisface la propiedad de aproximación atada. El primer ejemplo de Enflo de un espacio que falló la propiedad de aproximación fue al mismo tiempo el primer ejemplo de un espacio separado de Banach sin una base Schauder.

Robert C. James caracterizó la reflexividad en los espacios de Banach con una base: el espacio $X$ con una base Schauder es reflexivo si y sólo si la base es encogedora y terminada. En este caso, las funciones biorthogonales forman una base de la dualidad de $X.$

Producto tensor

Vamos $X$ y $Y$ dos $mathbb {K}$ - Espacios vencedores. El producto tensor $Xotimes Y$ de $X$ y $Y$ es un $mathbb {K}$ - Espacio de vehículos $Z$ con una asignación bilineal ${displaystyle T:Xtimes Yto Z}$ que tiene la siguiente propiedad universal:

{displaystyle T_{1}:Xtimes Yto Z_{1}}

es cualquier cartografía bilineal en un

mathbb {K}

- Espacio de vehículos

{displaystyle Z_{1},}

entonces existe una asignación lineal única

{displaystyle f:Zto Z_{1}}

tales que

{displaystyle T_{1}=fcirc T.}

La imagen bajo $T$ de un par $(x,y)$ dentro $Xtimes Y$ es denotado por ${displaystyle xotimes y,}$ y llamó a simple tensor. Cada elemento $z$ dentro $Xotimes Y$ es una suma finita de tan simple tensores.

Hay varias normas que se pueden colocar en el producto tensorial de los espacios vectoriales subyacentes, entre otras, la norma cruzada proyectiva y la norma cruzada inyectiva introducidas por A. Grothendieck en 1955.

En general, el producto tensor de los espacios completos no se completa de nuevo. Al trabajar con los espacios de Banach, es habitual decir que producto de tensor proyector de dos espacios de Banach $X$ y $Y$ es finalización $X{widehat {otimes }}_{pi }Y$ del producto algebraico tensor $Xotimes Y$ equipado con la norma de tensor proyectiva, y similarmente para la producto de tensor inyectable ${displaystyle X{widehat {otimes }}_{varepsilon }Y.}$ Grothendieck demostró en particular que

{displaystyle {begin{aligned}C(K){widehat {otimes }}_{varepsilon }Y&simeq C(K,Y),\L^{1}([0,1]){widehat {otimes }}_{pi }Y&simeq L^{1}([0,1],Y),end{aligned}}}

K

{displaystyle C(K,Y)}

K

Y

{displaystyle L^{1}([0,1],Y)}

[0,1]

Y,

{displaystyle fotimes y}

{displaystyle sin Kto f(s)yin Y.}

Productos tensoriales y propiedad de aproximación

Vamos $X$ ser un espacio de Banach. El producto tensor $X'{widehat {otimes }}_{varepsilon }X$ se identifica isométricamente con el cierre en ${displaystyle B(X)}$ del conjunto de operadores de rango finito. Cuando $X$ tiene la propiedad de aproximación, este cierre coincide con el espacio de operadores compactos en $X.$

Por cada espacio de Banach $Y,$ hay una norma natural $1$ mapa lineal

{displaystyle Y{widehat {otimes }}_{pi }Xto Y{widehat {otimes }}_{varepsilon }X}

Y

X.

X,

{displaystyle X'{widehat {otimes }}_{pi }X longrightarrow X'{widehat {otimes }}_{varepsilon }X}

X

Grothendieck conjetura que $X{widehat {otimes }}_{pi }Y$ y $X{widehat {otimes }}_{varepsilon }Y$ debe ser diferente $X$ y $Y$ son espacios de Banach infinitamente dimensionados. Esto fue refutado por Gilles Pisier en 1983. Pisier construyó un espacio de Banach infinita $X$ tales que $X{widehat {otimes }}_{pi }X$ y $X{widehat {otimes }}_{varepsilon }X$ son iguales. Además, como ejemplo de Enflo, este espacio $X$ es un espacio hecho a mano que no tiene la propiedad de aproximación. Por otro lado, Szankowski demostró que el espacio clásico ${displaystyle Bleft(ell ^{2}right)}$ no tiene la propiedad de aproximación.

Algunos resultados de clasificación

Caracterizaciones del espacio de Hilbert entre los espacios de Banach

Una condición necesaria y suficiente para la norma de un espacio de Banach $X$ estar asociado a un producto interno es la identidad paralelograma:

Identidad parallelograma—para todos ${displaystyle x,yin X:qquad |x+y|^{2}+|x-y|^{2}=2left(|x|^{2}+|y|^{2}right).}$

Por ejemplo, sigue que el espacio Lebesgue ${displaystyle L^{p}([0,1])}$ es un espacio de Hilbert sólo cuando ${displaystyle p=2.}$ Si esta identidad está satisfecha, el producto interno asociado es dado por la identidad de polarización. En el caso de los cuero cabelludos reales, esto da:

{displaystyle langle x,yrangle ={tfrac {1}{4}}left(|x+y|^{2}-|x-y|^{2}right).}

Para los escalares complejos, definiendo el producto interior para ser $mathbb{C}$ -linear en $x,$ antilinear en $y,$ la identidad de polarización da:

{displaystyle langle x,yrangle ={tfrac {1}{4}}left(|x+y|^{2}-|x-y|^{2}+ileft(|x+iy|^{2}-|x-iy|^{2}right)right).}

Para ver que la ley paralela es suficiente, se observa en el caso real que $langle x, y rangle$ es simétrico, y en el caso complejo, que satisface la propiedad de la simetría hermitiana y ${displaystyle langle ix,yrangle =ilangle x,yrangle.}$ La ley paralela implica que $langle x, y rangle$ es aditivo en $x.$ Se deduce que es lineal sobre los racionales, por lo tanto lineal por la continuidad.

Existen varias caracterizaciones de espacios isomorfos (en vez de isométricos) a Hilbert espacios disponibles. La ley paralela puede extenderse a más de dos vectores y debilitarse por la introducción de una desigualdad de dos lados con una constante ${displaystyle cgeq 1}$ Kwapień demostró que si

{displaystyle c^{-2}sum _{k=1}^{n}left|x_{k}right|^{2}leq operatorname {Ave} _{pm }left|sum _{k=1}^{n}pm x_{k}right|^{2}leq c^{2}sum _{k=1}^{n}left|x_{k}right|^{2}}

n

{displaystyle left{x_{1},ldotsx_{n}right}subseteq X,}

X

{displaystyle operatorname {Ave} _{pm }}

2^{n}

{displaystyle pm 1.}

Lindenstrauss y Tzafriri demostraron que un espacio de Banach en el que se complementa cada subespacio lineal cerrado (es decir, es la gama de una proyección lineal atada) es isomorfo a un espacio de Hilbert. La prueba se basa en el teorema de Dvoretzky sobre secciones euclidianas de cuerpos convexos centralmente simétricos de alta dimensión. En otras palabras, el teorema de Dvoretzky afirma que por cada entero ${displaystyle n,}$ cualquier espacio fijo-dimensional, con dimensión suficientemente grande ${displaystyle n,}$ contiene subespacios casi isométricos al $n$ -dimensional Espacio euclidiano.

El siguiente resultado da la solución del llamado problema espacial homogéneo. Un espacio de Banach infinita $X$ se dice que homogénea si es isomorfo a todos sus subespacios cerrados de dimensiones infinitas. Un espacio de Banach isomorfo a $ell ^{2}$ es homogénea, y Banach pidió el contrario.

Theorem—Un espacio de Banach isomorfo a todos sus subespacios cerrados de dimensiones infinitas es isomorfo a un espacio separable de Hilbert.

Un espacio de banca infinita es hereditariamente indecomposible cuando ningún subespacio puede ser isomorfo a la suma directa de dos espacios de Banach infinitamente dimensionados. El teorema de dicotomía Gowers afirma que cada espacio de Banach infinito $X$ contiene, ya sea un subespacio $Y$ con base incondicional, o un subespacial hereditariamente indecompuesto $Z,$ y en particular, $Z$ no es isomorfo a sus hiperplanos cerrados. Si $X$ es homogénea, por lo tanto debe tener una base incondicional. A continuación, de la solución parcial obtenida por Komorowski y Tomczak-Jaegermann, para espacios con una base incondicional, que $X$ es isomorfo a ${displaystyle ell ^{2}.}$

Clasificación métrica

Si ${displaystyle T:Xto Y}$ es una isometría del espacio de Banach $X$ sobre el espacio de Banach $Y$ (donde ambos $X$ y $Y$ son espacios vectoriales sobre $mathbb {R}$ ), entonces el teorema de Mazur-Ulam declara que $T$ debe ser una transformación afinada. En particular, si ${displaystyle T(0_{X})=0_{Y},}$ esto es $T$ mapas el cero de $X$ al cero de $Y,$ entonces $T$ Debe ser lineal. Este resultado implica que la métrica en los espacios de Banach, y más generalmente en espacios ordenados, captura completamente su estructura lineal.

Clasificación topológica

Los espacios de Banach de dimensión finita son homeomorfos como espacios topológicos, si y solo si tienen la misma dimensión que los espacios vectoriales reales.

El teorema de Anderson-Kadec (1965-1966) demuestra que cualquier espacio de Banach separable de dos dimensiones infinitas es homeomorfo como espacio topológico. El teorema de Kadec fue ampliado por Torunczyk, quien demostró que dos espacios de Banach cualesquiera son homeomorfos si y solo si tienen el mismo carácter de densidad, la cardinalidad mínima de un subconjunto denso.

Espacios de funciones continuas

Cuando dos espacios compactos Hausdorff $K_{1}$ y $K_{2}$ son homeomorfos, los espacios de Banach ${displaystyle Cleft(K_{1}right)}$ y ${displaystyle Cleft(K_{2}right)}$ son isométricos. Por el contrario, cuando $K_{1}$ no es homeomorfo a ${displaystyle K_{2},}$ la distancia (multiplicativa) Banach–Mazur entre ${displaystyle Cleft(K_{1}right)}$ y ${displaystyle Cleft(K_{2}right)}$ debe ser mayor o igual a ${displaystyle 2,}$ ver por encima de los resultados de Amir y Cambern. Aunque espacios métricos compactos incontables pueden tener diferentes tipos de homeomorfia, uno tiene el siguiente resultado debido a Milutin:

Theorem—Vamos $K$ ser un espacio métrico compacto incontable. Entonces... $C(K)$ es isomorfo a ${displaystyle C([0,1]).}$

La situación es diferente para espacios compactos Hausdorff contablemente infinitos. Cada compacto contablemente infinito $K$ es homeomorfo a algún intervalo cerrado de números ordinal

{displaystyle langle 1,alpha rangle ={gamma : 1leq gamma leq alpha }}

alpha

C(K)

C . α .

alphabeta

{displaystyle alpha leq beta}

C . α .

C . β .

β . α \cdot

{displaystyle C(langle 1,omega rangle), C(langle 1,omega ^{omega }rangle), C(langle 1,omega ^{omega ^{2}}rangle), C(langle 1,omega ^{omega ^{3}}rangle),cdotsC(langle 1,omega ^{omega ^{omega }}rangle),cdots }

Ejemplos

Glosario de símbolos para la siguiente tabla:

$mathbb {F}$ denota el campo de números reales $mathbb {R}$ o números complejos ${displaystyle mathbb {C}.}$
$K$ es un espacio compacto Hausdorff.
${displaystyle p,qin mathbb {R} }$ son números reales con $<math alttext="{displaystyle 1<p,q1.p,q.JUEGO JUEGO {displaystyle 1 sep,q segÃ3n] <img alt="{displaystyle 1<p,q$ que son conjugados Hölder, que significa que satisfacen ${displaystyle {frac {1}{q}}+{frac {1}{p}}=1}$ y así también ${displaystyle q={frac {p}{p-1}}.}$
$Sigma$ es un $sigma$ - álgebra de conjuntos.
$Xi$ es un álgebra de conjuntos (para espacios que sólo requieren aditividad finita, como el espacio ba).
$mu$ es una medida con variación ${displaystyle |mu |.}$ Una medida positiva es una función de conjunto positiva de valor real definida en una $sigma$ - álgebra que es contablemente aditivo.

	Espacio dual	Reflexivo	débilmente secuencialmente completo	Norm		Notas
Espacios de Banach Clásicos
${mathbb {F}}^{n}$	${mathbb {F}}^{n}$	Sí.	Sí.	$\|x\|_{2}$	${displaystyle =left(sum _{i=1}^{n}\|x_{i}\|^{2}right)^{1/2}}$	Espacio euclidiano
${displaystyle ell _{p}^{n}}$	${displaystyle ell _{q}^{n}}$	Sí.	Sí.	${displaystyle \|x\|_{p}}$	${displaystyle =left(sum _{i=1}^{n}\|x_{i}\|^{p}right)^{frac {1}{p}}}$
${displaystyle ell _{infty }^{n}}$	${displaystyle ell _{1}^{n}}$	Sí.	Sí.	${displaystyle \|x\|_{infty }}$	${displaystyle =max nolimits _{1leq ileq n}\|x_{i}\|}$
$ell ^{p}$	$ell ^{q}$	Sí.	Sí.	${displaystyle \|x\|_{p}}$	${displaystyle =left(sum _{i=1}^{infty }\|x_{i}\|^{p}right)^{frac {1}{p}}}$
$ell ^{1}$	${displaystyle ell ^{infty }}$	No	Sí.	${displaystyle \|x\|_{1}}$	${displaystyle =sum _{i=1}^{infty }left\|x_{i}right\|}$
${displaystyle ell ^{infty }}$	${displaystyle operatorname {ba} }$	No	No	${displaystyle \|x\|_{infty }}$	${displaystyle =sup nolimits _{i}left\|x_{i}right\|}$
${displaystyle operatorname {c} }$	$ell ^{1}$	No	No	${displaystyle \|x\|_{infty }}$	${displaystyle =sup nolimits _{i}left\|x_{i}right\|}$
$c_{0}$	$ell ^{1}$	No	No	${displaystyle \|x\|_{infty }}$	${displaystyle =sup nolimits _{i}left\|x_{i}right\|}$	Isomorfo pero no isométrico $c.$
${displaystyle operatorname {bv} }$	${displaystyle ell ^{infty }}$	No	Sí.	${displaystyle \|x\|_{bv}}$	${displaystyle =left\|x_{1}right\|+sum _{i=1}^{infty }left\|x_{i+1}-x_{i}right\|}$	Isometrically isomorfo a ${displaystyle ell ^{1}.}$
${displaystyle operatorname {bv} _{0}}$	${displaystyle ell ^{infty }}$	No	Sí.	${displaystyle \|x\|_{bv_{0}}}$	${displaystyle =sum _{i=1}^{infty }left\|x_{i+1}-x_{i}right\|}$	Isometrically isomorfo a ${displaystyle ell ^{1}.}$
${displaystyle operatorname {bs} }$	${displaystyle operatorname {ba} }$	No	No	${displaystyle \|x\|_{bs}}$	${displaystyle =sup nolimits _{n}left\|sum _{i=1}^{n}x_{i}right\|}$	Isometrically isomorfo a ${displaystyle ell ^{infty }.}$
${displaystyle operatorname {cs} }$	$ell ^{1}$	No	No	${displaystyle \|x\|_{bs}}$	${displaystyle =sup nolimits _{n}left\|sum _{i=1}^{n}x_{i}right\|}$	Isometrically isomorfo a $c.$
${displaystyle B(K,Xi)}$	${displaystyle operatorname {ba} (Xi)}$	No	No	${displaystyle \|f\|_{B}}$	${displaystyle =sup nolimits _{kin K}\|f(k)\|}$
$C(K)$	${displaystyle operatorname {rca} (K)}$	No	No	${displaystyle \|x\|_{C(K)}}$	${displaystyle =max nolimits _{kin K}\|f(k)\|}$
${displaystyle operatorname {ba} (Xi)}$	?	No	Sí.	${displaystyle \|mu \|_{ba}}$	${displaystyle =sup nolimits _{Sin Sigma }\|mu \|(S)}$
${displaystyle operatorname {ca} (Sigma)}$	?	No	Sí.	${displaystyle \|mu \|_{ba}}$	${displaystyle =sup nolimits _{Sin Sigma }\|mu \|(S)}$	Un subespacio cerrado ${displaystyle operatorname {ba} (Sigma).}$
${displaystyle operatorname {rca} (Sigma)}$	?	No	Sí.	${displaystyle \|mu \|_{ba}}$	${displaystyle =sup nolimits _{Sin Sigma }\|mu \|(S)}$	Un subespacio cerrado ${displaystyle operatorname {ca} (Sigma).}$
${displaystyle L^{p}(mu)}$	${displaystyle L^{q}(mu)}$	Sí.	Sí.	${displaystyle \|f\|_{p}}$	${displaystyle =left(int \|f\|^{p},dmu right)^{frac {1}{p}}}$
$L^1(mu)$	${displaystyle L^{infty }(mu)}$	No	Sí.	${displaystyle \|f\|_{1}}$	${displaystyle =int \|f\|,dmu }$	El dual es ${displaystyle L^{infty }(mu)}$ si $mu$ es $sigma$ - Claro..
${displaystyle operatorname {BV} ([a,b])}$	?	No	Sí.	${displaystyle \|f\|_{BV}}$	${displaystyle =V_{f}([a,b])+lim nolimits _{xto a^{+}}f(x)}$	${displaystyle V_{f}([a,b]).}$ es la variación total de $f$
${displaystyle operatorname {NBV} ([a,b])}$	?	No	Sí.	${displaystyle \|f\|_{BV}}$	${displaystyle =V_{f}([a,b])}$	${displaystyle operatorname {NBV} ([a,b])}$ consta de ${displaystyle operatorname {BV} ([a,b])}$ funciones tales como ${displaystyle lim nolimits _{xto a^{+}}f(x)=0}$
${displaystyle operatorname {AC} ([a,b])}$	${displaystyle mathbb {F} +L^{infty }([a,b])}$	No	Sí.	${displaystyle \|f\|_{BV}}$	${displaystyle =V_{f}([a,b])+lim nolimits _{xto a^{+}}f(x)}$	Isomorfa al espacio Sobolev ${displaystyle W^{1,1}([a,b]).}$
${displaystyle C^{n}([a,b])}$	${displaystyle operatorname {rca} ([a,b])}$	No	No	${displaystyle \|f\|}$	${displaystyle =sum _{i=0}^{n}sup nolimits _{xin [a,b]}left\|f^{(i)}(x)right\|}$	Isomorfo a ${displaystyle mathbb {R} ^{n}oplus C([a,b]),}$ esencialmente por el teorema de Taylor.

Derivados

Se pueden definir varios conceptos de una derivada en un espacio de Banach. Ver los artículos sobre el derivado Fréchet y el derivado Gateaux para más detalles. La derivada de Fréchet permite extender el concepto de derivada total a los espacios de Banach. La derivada de Gateaux permite una extensión de una derivada direccional a espacios vectoriales topológicos localmente convexos. La diferenciabilidad de Fréchet es una condición más fuerte que la diferenciabilidad de Gateaux. La cuasi-derivada es otra generalización de la derivada direccional que implica una condición más fuerte que la diferenciabilidad de Gateaux, pero una condición más débil que la diferenciabilidad de Fréchet.

Generalizaciones

Varios espacios importantes en el análisis funcional, por ejemplo el espacio de todas las funciones infinitamente a menudo diferenciables ${displaystyle mathbb {R} to mathbb {R}}$ o el espacio de todas las distribuciones en ${displaystyle mathbb {R}}$ son completos pero no son espacios vectoriales ordenados y por lo tanto no espacios de Banach. En los espacios Fréchet uno todavía tiene una métrica completa, mientras que los espacios LF son espacios vectoriales completos que surgen como límites de los espacios Fréchet.

Te puede interesar
Teoría del nudo
En el campo matemático de la topología, teoría del nudo es el estudio de nudos matemáticos. Mientras se inspira en nudos que aparecen en la vida diaria... (leer más)
Te puede interesar
Fórmula de De Moivre
(leer más)
Te puede interesar
Imre lakatos
(leer más)
Más resultados...

Espacio de banach

Definición

Topología

Integridad

Terminaciones

Teoría general

Operadores lineales, isomorfismos

Funciones lineales continuas y acotadas y seminormas

Nociones básicas

Espacios clásicos

Álgebras de Banach

Ejemplos

Doble espacio

Topologías débiles

Ejemplos de espacios duales

Bidual

Teoremas de Banach

Reflexividad

Débil convergencia de secuencias

Resultados relacionados con la ℓ 1 { estilo de visualización ell ^ {1}} base

Secuencias, compacidad débil y débil*

Bases Schauder

Producto tensor

Productos tensoriales y propiedad de aproximación

Algunos resultados de clasificación

Caracterizaciones del espacio de Hilbert entre los espacios de Banach

Clasificación métrica

Clasificación topológica

Espacios de funciones continuas

Ejemplos

Derivados

Generalizaciones

Teoría del nudo

Fórmula de De Moivre

Imre lakatos