Esfuerzo de torsión

format_list_bulleted Contenido keyboard_arrow_down

ImprimirCitar

Concepto físico

En física y mecánica, torque es el equivalente rotativo de la fuerza lineal. It is also referred to as the momento de la fuerza (también abreviado a momento). Representa la capacidad de una fuerza para producir cambio en el movimiento rotacional del cuerpo. El concepto se originó con los estudios de Arquímedes del uso de palancas, que se refleja en su famosa cita: "Dame una palanca y un lugar para estar y moveré la Tierra". Al igual que una fuerza lineal es un empujón o un tirón, un par puede ser pensado como un giro a un objeto alrededor de un eje específico. Torque se define como el producto de la magnitud del componente perpendicular de la fuerza y la distancia de la línea de acción de una fuerza desde el punto alrededor del cual se está determinando. La ley de conservación de la energía también se puede utilizar para entender el par. El símbolo del par es típicamente ${boldsymbol {tau }}$ , la carta griega inferior tau. Al ser referido como momento de fuerza, es comúnmente denotado por $M$ .

En tres dimensiones, el par es un pseudovector; para partículas puntuales, viene dado por el producto cruzado del vector de posición (vector de distancia) y el vector de fuerza. La magnitud del par de torsión de un cuerpo rígido depende de tres cantidades: la fuerza aplicada, el vector de brazo de palanca que conecta el punto alrededor del cual se mide el par de torsión con el punto de aplicación de la fuerza, y el ángulo entre el vectores de fuerza y brazo de palanca. En símbolos:

{boldsymbol {tau }}=mathbf {r} times mathbf {F} ,!

tau =|mathbf {r} |,|mathbf {F} |sin theta ,!

dónde

${boldsymbol {tau }}$ es el vector de par y $tau$ es la magnitud del par,
$mathbf {r}$ es el vector de posición (un vector desde el punto en que se mide el par hasta el punto en que se aplica la fuerza),
$mathbf {F}$ es el vector de fuerza,
$times$ denota el producto cruzado, que produce un vector perpendicular a ambos $r$ y $F$ siguiendo la regla de la mano derecha,
$theta$ es el ángulo entre el vector de fuerza y el vector del brazo de palanca.

La unidad SI para el torque es el newton-metro (N⋅m). Para obtener más información sobre las unidades de par, consulte § Unidades.

Historia

Se dice que el término torque (del latín torquēre "torcer") fue sugerido por James Thomson y apareció impreso en abril, 1884. El uso es atestiguado el mismo año por Silvanus P. Thompson en la primera edición de Dynamo-Electric Machinery. Thompson motiva el término de la siguiente manera:

Como la definición de Newtonian fuerza es lo que produce o tiende a producir movimiento (a lo largo de una línea), así torque puede definirse como lo que produce o tiende a producir torsión (en torno a un eje). Es mejor utilizar un término que trata esta acción como una sola entidad definida que usar términos como "couple" y "moment", que sugieren ideas más complejas. La idea única de un giro aplicado para girar un eje es mejor que la noción más compleja de aplicar una fuerza lineal (o un par de fuerzas) con cierto apalancamiento.

Hoy en día, se hace referencia a la torsión utilizando un vocabulario diferente según la ubicación geográfica y el campo de estudio. Este artículo sigue la definición utilizada en la física de EE. UU. en el uso de la palabra torque.

En la ingeniería mecánica del Reino Unido y los EE. UU., el par se denomina momento de fuerza, generalmente abreviado como momento. Esta terminología se remonta al menos a 1811 en el Traité de mécanique de Siméon Denis Poisson. Una traducción al inglés del trabajo de Poisson aparece en 1842.

Definición y relación con el momento angular

Una partícula se encuentra en posición r relativo a su eje de rotación. Cuando una fuerza F se aplica a la partícula, sólo el componente perpendicular F_⊥ produce un par. Esta torsión

τ = r \times F

de magnitud

τ = Silencio r Silencio F ⊥ Silencio r Silencio F pecado Silencio

y se dirige hacia fuera desde la página.

Una fuerza aplicada perpendicularmente a una palanca multiplicada por su distancia desde el punto de apoyo de la palanca (la longitud del brazo de la palanca) es su par. Una fuerza de tres newtons aplicada a dos metros del punto de apoyo, por ejemplo, ejerce el mismo par que una fuerza de un newton aplicada a seis metros del punto de apoyo. La dirección del par se puede determinar utilizando la regla de agarre de la mano derecha: si los dedos de la mano derecha están doblados desde la dirección del brazo de palanca hacia la dirección de la fuerza, entonces el pulgar apunta en la dirección del par.

De manera más general, el momento de torsión en una partícula puntual (que tiene la posición r en algún marco de referencia) se puede definir como el producto vectorial:

{boldsymbol {tau }}=mathbf {r} times mathbf {F}

donde F es la fuerza que actúa sobre la partícula. La magnitud τ del par viene dada por

{displaystyle tau =rFsin theta}

donde F es la magnitud de la fuerza aplicada, y θ es el ángulo entre los vectores de posición y fuerza. Alternativamente,

tau =rF_{perp },

donde F_⊥ es la cantidad de fuerza dirigida perpendicularmente a la posición de la partícula. Cualquier fuerza dirigida paralelamente al vector de posición de la partícula no produce un par.

Se deduce de las propiedades del producto vectorial que el vector de torsión es perpendicular a los vectores de posición y fuerza. Por el contrario, el vector par define el plano en el que se encuentran los vectores posición y fuerza. La dirección del vector de torsión resultante está determinada por la regla de la mano derecha.

El par neto sobre un cuerpo determina la tasa de cambio del momento angular del cuerpo,

{boldsymbol {tau }}={frac {mathrm {d} mathbf {L} }{mathrm {d} t}}

donde L es el vector de momento angular y t es el tiempo.

Para el movimiento de una partícula puntual,

mathbf {L} =I{boldsymbol {omega }},

donde $I$ es el momento de inercia y ω es el pseudovector de velocidad angular orbital. Resulta que

{displaystyle {boldsymbol {tau }}_{mathrm {net} }={frac {mathrm {d} mathbf {L} }{mathrm {d} t}}={frac {mathrm {d} (I{boldsymbol {omega }})}{mathrm {d} t}}=I{frac {mathrm {d} {boldsymbol {omega }}}{mathrm {d} t}}+{frac {mathrm {d} I}{mathrm {d} t}}{boldsymbol {omega }}=I{boldsymbol {alpha }}+{frac {mathrm {d} (mr^{2})}{mathrm {d} t}}{boldsymbol {omega }}=I{boldsymbol {alpha }}+2rp_{||}{boldsymbol {omega }},}

donde α es la aceleración angular de la partícula, y p_|| es la componente radial de su momento lineal. Esta ecuación es el análogo rotacional de la segunda ley de Newton para partículas puntuales y es válida para cualquier tipo de trayectoria. Tenga en cuenta que aunque la fuerza y la aceleración son siempre paralelas y directamente proporcionales, el par τ no necesita ser paralelo o directamente proporcional a la aceleración angular α. Esto surge del hecho de que aunque la masa siempre se conserva, el momento de inercia en general no lo es.

En algunos casos simples, como un disco giratorio, el momento de inercia es una constante, la segunda ley de Newton rotacional puede ser

{displaystyle {boldsymbol {tau }}=I{boldsymbol {alpha }}}

{textstyle I=mr^{2}}

{displaystyle {boldsymbol {alpha }}={d{boldsymbol {omega }} over dt}}

Prueba de la equivalencia de definiciones

La definición de momento angular para una partícula de un solo punto es:

{displaystyle mathbf {L} =mathbf {r} times mathbf {p} }

{displaystyle {frac {mathrm {d} mathbf {L} }{mathrm {d} t}}=mathbf {r} times {frac {mathrm {d} mathbf {p} }{mathrm {d} t}}+{frac {mathrm {d} mathbf {r} }{mathrm {d} t}}times mathbf {p}.}

Este resultado se puede probar fácilmente dividiendo los vectores en componentes y aplicando la regla del producto. Ahora utilizando la definición de fuerza ${textstyle mathbf {F} ={frac {mathrm {d} mathbf {p} }{mathrm {d} t}}}$ (ya sea o no la masa es constante) y la definición de velocidad ${textstyle {frac {mathrm {d} mathbf {r} }{mathrm {d} t}}=mathbf {v} }$

{displaystyle {frac {mathrm {d} mathbf {L} }{mathrm {d} t}}=mathbf {r} times mathbf {F} +mathbf {v} times mathbf {p}.}

El producto cruzado del impulso $mathbf {p}$ con su velocidad asociada $mathbf {v}$ es cero porque la velocidad y el impulso son paralelos, por lo que el segundo término desaparece.

Por definición, par τ = r × F. Por lo tanto, el torque en una partícula es igual al primera derivada de su momento angular con respecto al tiempo.

Si se aplican múltiples fuerzas, la segunda ley de Newton dice F_net = ma, y se sigue que

{displaystyle {frac {mathrm {d} mathbf {L} }{mathrm {d} t}}=mathbf {r} times mathbf {F} _{mathrm {net} }={boldsymbol {tau }}_{mathrm {net} }.}

Esta es una prueba general para partículas puntuales.

La prueba se puede generalizar a un sistema de partículas puntuales aplicando la prueba anterior a cada una de las partículas puntuales y luego sumando todas las partículas puntuales. De manera similar, la prueba se puede generalizar a una masa continua aplicando la prueba anterior a cada punto dentro de la masa y luego integrando sobre toda la masa.

Unidades

El par tiene la dimensión de la fuerza por la distancia, simbólicamente T⁻²L²M. Aunque esas dimensiones fundamentales son las mismas que para la energía o el trabajo, la literatura oficial del SI sugiere usar la unidad newton-metro (N⋅m) y nunca el julio. La unidad newton-metro se denota correctamente como N⋅m.

Las unidades tradicionales imperiales y estadounidenses para el torque son la libra pie (lbf-ft) o, para valores pequeños, la libra pulgada (lbf-in). En los EE. UU., el par se denomina más comúnmente como pie-libra (indicado como lb-ft o ft-lb) y pulgada-libra (indicado como en -lb). Los practicantes dependen del contexto y el guión en la abreviatura para saber que estos se refieren a torque y no a energía o momento de masa (como implicaría correctamente el simbolismo ft-lb).

Casos especiales y otros hechos

Fórmula de brazo de momento

Diagrama del brazo del movimiento

Un caso especial muy útil, a menudo dado como la definición de torque en campos distintos a la física, es el siguiente:

tau =({text{moment arm}})({text{force}}).

La construcción del "brazo de momento" se muestra en la figura de la derecha, junto con los vectores r y F mencionados anteriormente. El problema con esta definición es que no da la dirección del par sino solo la magnitud y, por lo tanto, es difícil de usar en casos tridimensionales. Si la fuerza es perpendicular al vector de desplazamiento r, el brazo de momento será igual a la distancia al centro y el par será el máximo para la fuerza dada. La ecuación para la magnitud de un momento de torsión, que surge de una fuerza perpendicular:

tau =({text{distance to centre}})({text{force}}).

Por ejemplo, si una persona aplica una fuerza de 10 N en el extremo terminal de una llave de 0,5 m de largo (o una fuerza de 10 N que actúa a 0,5 m del punto de torsión de una llave de cualquier longitud), el el par será de 5 N⋅m, suponiendo que la persona mueva la llave aplicando fuerza en el plano de movimiento y perpendicular a la llave.

El par causado por las dos fuerzas opuestas F_g and −F_g provoca un cambio en el impulso angular L en la dirección de ese par. Esto hace que la parte superior preceda.

Equilibrio estático

Para que un objeto esté en equilibrio estático, no solo la suma de las fuerzas debe ser cero, sino también la suma de los pares (momentos) en cualquier punto. Para una situación bidimensional con fuerzas horizontales y verticales, la suma de los requisitos de fuerzas es dos ecuaciones: $Σ H = 0$ y $Σ V = 0$ , y el torque una tercera ecuación: $Σ τ = 0$ . Es decir, para resolver problemas de equilibrio estáticamente determinados en dos dimensiones se utilizan tres ecuaciones.

Fuerza neta frente a par

Cuando la fuerza neta en el sistema es cero, el par medido desde cualquier punto en el espacio es el mismo. Por ejemplo, el par en un bucle de carga actual en un campo magnético uniforme es el mismo independientemente del punto de referencia. Si la fuerza neta $mathbf {F}$ no es cero, y ${boldsymbol {tau }}_{1}$ es el par medido desde $mathbf {r} _{1}$ , entonces el par medida desde $mathbf {r} _{2}$ es

{displaystyle {boldsymbol {tau }}_{2}={boldsymbol {tau }}_{1}+(mathbf {r} _{1}-mathbf {r} _{2})times mathbf {F} }

Par de la máquina

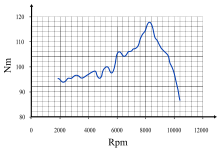
Curva Torque de una moto ("BMW K 1200 R 2005"). El eje horizontal muestra la velocidad (en rpm) que el crankshaft está girando, y el eje vertical es el par (en newton-metres) que el motor es capaz de proporcionar a esa velocidad.

El par forma parte de la especificación básica de un motor: la potencia de salida de un motor se expresa como su par multiplicado por la velocidad angular del eje de transmisión. Los motores de combustión interna producen un par útil solo en un rango limitado de velocidades de rotación (normalmente, entre 1000 y 6000 rpm para un coche pequeño). Se puede medir la salida de torsión variable en ese rango con un dinamómetro y mostrarla como una curva de torsión.

Los motores de vapor y los motores eléctricos tienden a producir un par máximo cercano a cero rpm, y el par disminuye a medida que aumenta la velocidad de rotación (debido al aumento de la fricción y otras limitaciones). Los motores de vapor alternativos y los motores eléctricos pueden arrancar cargas pesadas desde cero rpm sin embrague.

Relación entre par, potencia y energía

Si se permite que una fuerza actúe a lo largo de una distancia, está realizando un trabajo mecánico. De manera similar, si se permite que el par actúe a través de un desplazamiento angular, está realizando trabajo. Matemáticamente, para la rotación alrededor de un eje fijo que pasa por el centro de masa, el trabajo W se puede expresar como

W=int _{theta _{1}}^{theta _{2}}tau mathrm {d} theta

donde τ es par, y θ₁ y θ₂ representan (respectivamente) las posiciones angulares inicial y final del cuerpo.

Prueba

El trabajo realizado por una fuerza variable que actúa sobre un desplazamiento lineal finito $s$ se da mediante la integración de la fuerza con respecto a un desplazamiento lineal elemental ${displaystyle mathrm {d} mathbf {s} }$

{displaystyle W=int _{s_{1}}^{s_{2}}mathbf {F} cdot mathrm {d} mathbf {s} }

Sin embargo, el desplazamiento lineal infinitesimal ${displaystyle mathrm {d} mathbf {s} }$ está relacionado con un desplazamiento angular correspondiente ${displaystyle mathrm {d} {boldsymbol {theta }}}$ y el vector del radio $mathbf {r}$ como

{displaystyle mathrm {d} mathbf {s} =mathrm {d} {boldsymbol {theta }}times mathbf {r} }

La sustitución en la expresión anterior por trabajo da

{displaystyle W=int _{s_{1}}^{s_{2}}mathbf {F} cdot mathrm {d} {boldsymbol {theta }}times mathbf {r} }

La expresión ${displaystyle mathbf {F} cdot mathrm {d} {boldsymbol {theta }}times mathbf {r} }$ es un producto triple escalar dado por ${displaystyle left[mathbf {F} ,mathrm {d} {boldsymbol {theta }},mathbf {r} right]}$ . Una expresión alternativa para el mismo producto triple escalar

{displaystyle left[mathbf {F} ,mathrm {d} {boldsymbol {theta }},mathbf {r} right]=mathbf {r} times mathbf {F} cdot mathrm {d} {boldsymbol {theta }}}

Pero según la definición de torque,

{displaystyle {boldsymbol {tau }}=mathbf {r} times mathbf {F} }

La sustitución correspondiente en la expresión de trabajo da,

{displaystyle W=int _{s_{1}}^{s_{2}}{boldsymbol {tau }}cdot mathrm {d} {boldsymbol {theta }}}

Dado que el parámetro de integración ha cambiado de desplazamiento lineal a desplazamiento angular, los límites de la integración también cambian correspondientemente, dando

{displaystyle W=int _{theta _{1}}^{theta _{2}}{boldsymbol {tau }}cdot mathrm {d} {boldsymbol {theta }}}

Si el par y el desplazamiento angular están en la misma dirección, el producto del cuero cabelludo reduce a un producto de magnitudes; es decir, ${displaystyle {boldsymbol {tau }}cdot mathrm {d} {boldsymbol {theta }}=left|{boldsymbol {tau }}right|left|mathrm {d} {boldsymbol {theta }}right|cos 0=tau ,mathrm {d} theta }$ dar

{displaystyle W=int _{theta _{1}}^{theta _{2}}tau ,mathrm {d} theta }

Se sigue del principio de trabajo-energía que W también representa el cambio en la energía cinética rotacional E_r del cuerpo, dada por

E_{mathrm {r} }={tfrac {1}{2}}Iomega ^{2},

donde I es el momento de inercia del cuerpo y ω es su velocidad angular.

La potencia es el trabajo por unidad de tiempo, dado por

{displaystyle P={boldsymbol {tau }}cdot {boldsymbol {omega }},}

Donde P es poder, τ es torque, ⋅ es la velocidad angular, y $cdot$ representa el producto del cuero cabelludo.

Algebraicamente, la ecuación se puede reorganizar para calcular el par para una velocidad angular y potencia de salida dadas. Tenga en cuenta que la potencia inyectada por el par depende solo de la velocidad angular instantánea, no de si la velocidad angular aumenta, disminuye o permanece constante mientras se aplica el par (esto es equivalente al caso lineal donde la potencia inyectada por una fuerza depende solo de la velocidad instantánea, no de la aceleración resultante, si la hay).

En la práctica, esta relación se puede observar en las bicicletas: las bicicletas generalmente se componen de dos ruedas de carretera, engranajes delanteros y traseros (denominados ruedas dentadas) que se engranan con una cadena y un mecanismo de desviador si la transmisión de la bicicleta El sistema permite el uso de múltiples relaciones de transmisión (es decir, bicicleta de varias velocidades), todas las cuales están unidas al cuadro. Un ciclista, la persona que monta la bicicleta, proporciona la potencia de entrada girando los pedales, haciendo girar así la rueda dentada delantera (comúnmente conocida como plato). La potencia de entrada proporcionada por el ciclista es igual al producto de la velocidad angular (es decir, el número de revoluciones del pedal por minuto por 2π) y el par en el eje del juego de bielas de la bicicleta. La transmisión de la bicicleta transmite la potencia de entrada a la rueda de la carretera, que a su vez transmite la potencia recibida a la carretera como potencia de salida de la bicicleta. Dependiendo de la relación de transmisión de la bicicleta, un par _{de entrada} (par, velocidad angular) se convierte en un par de _salida (par, velocidad angular). Al usar una marcha trasera más grande o al cambiar a una marcha más baja en bicicletas de varias velocidades, la velocidad angular de las ruedas de carretera disminuye mientras que el par aumenta, producto del cual (es decir, la potencia) no cambia.

Para las unidades SI, la unidad de potencia es el vatio, la unidad de torsión es el newton-metro y la unidad de velocidad angular es el radián por segundo (no rpm ni revoluciones por segundo).

La unidad newton-metro es dimensionalmente equivalente al joule, que es la unidad de energía. En el caso del par, la unidad se asigna a un vector, mientras que para la energía, se asigna a un escalar. Esto significa que la equivalencia dimensional del newton-metro y el joule se puede aplicar en el primer caso, pero no en el segundo. Este problema se aborda en el análisis orientacional, que trata al radián como una unidad base en lugar de una unidad adimensional.

Conversión a otras unidades

Puede ser necesario un factor de conversión cuando se utilizan diferentes unidades de potencia o par. Por ejemplo, si se utiliza la velocidad de rotación (revoluciones por tiempo) en lugar de la velocidad angular (radianes por tiempo), multiplicamos por un factor de 2 $π$ radianes por revolución. En las siguientes fórmulas, P es potencia, τ es par y ν (letra griega nu) es velocidad de rotación.

{displaystyle P=tau cdot 2pi cdot nu }

Mostrando unidades:

{displaystyle P_{rm {W}}=tau _{rm {N{cdot }m}}cdot 2pi _{rm {rad/rev}}cdot nu _{rm {rev/sec}}}

Dividir por 60 segundos por minuto nos da lo siguiente.

{displaystyle P_{rm {W}}={frac {tau _{rm {N{cdot }m}}cdot 2pi _{rm {rad/rev}}cdot nu _{rm {rpm}}}{60}}}

donde la velocidad de rotación está en revoluciones por minuto (rpm).

Algunas personas (por ejemplo, los ingenieros automotrices estadounidenses) usan caballos de fuerza (mecánicos) para potencia, libras-pie (lbf⋅ft) para torque y rpm para velocidad de rotación. Esto da como resultado que la fórmula cambie a:

{displaystyle P_{rm {hp}}={frac {tau _{rm {lbf{cdot }ft}}cdot 2pi _{rm {rad/rev}}cdot nu _{rm {rpm}}}{33,000}}.}

La siguiente constante (en libras-pie por minuto) cambia con la definición de caballos de fuerza; por ejemplo, utilizando caballos de fuerza métricos, se convierte en aproximadamente 32.550.

El uso de otras unidades (por ejemplo, BTU por hora para energía) requeriría un factor de conversión personalizado diferente.

Derivación

Para un objeto giratorio, la distancia lineal cubierta en la circunferencia de rotación es el producto del radio con el ángulo cubierto. Es decir: distancia lineal = radio × distancia angular. Y por definición, distancia lineal = velocidad lineal × tiempo = radio × velocidad angular × tiempo.

Según la definición de par: par = radio × fuerza. Podemos reorganizar esto para determinar fuerza = torque ÷ radio. Estos dos valores se pueden sustituir en la definición de poder:

{displaystyle {begin{aligned}{text{power}}&={frac {{text{force}}cdot {text{linear distance}}}{text{time}}}\[6pt]&={frac {left({dfrac {text{torque}}{r}}right)cdot (rcdot {text{angular speed}}cdot t)}{t}}\[6pt]&={text{torque}}cdot {text{angular speed}}.end{aligned}}}

El radio r y el tiempo t han desaparecido de la ecuación. Sin embargo, la velocidad angular debe estar en radianes por unidad de tiempo, por la supuesta relación directa entre la velocidad lineal y la velocidad angular al comienzo de la derivación. Si la velocidad de rotación se mide en revoluciones por unidad de tiempo, la velocidad lineal y la distancia aumentan proporcionalmente en 2 $π$ en lo anterior derivación para dar:

{displaystyle {text{power}}={text{torque}}cdot 2pi cdot {text{rotational speed}}.,}

Si el par está en newton-metros y la velocidad de rotación en revoluciones por segundo, la ecuación anterior da la potencia en newtons-metros por segundo o vatios. Si se utilizan unidades imperiales, y si el par está en libras-fuerza-pie y la velocidad de rotación en revoluciones por minuto, la ecuación anterior da la potencia en pie-libras-fuerza por minuto. Luego, la forma de caballos de fuerza de la ecuación se deriva aplicando el factor de conversión 33,000 ft⋅lbf/min por caballo de fuerza:

{displaystyle {begin{aligned}{text{power}}&={text{torque}}cdot 2pi cdot {text{rotational speed}}cdot {frac {{text{ft}}{cdot }{text{lbf}}}{text{min}}}cdot {frac {text{horsepower}}{33,000cdot {frac {{text{ft}}cdot {text{lbf}}}{text{min}}}}}\[6pt]&approx {frac {{text{torque}}cdot {text{RPM}}}{5,252}}end{aligned}}}

porque $5252.113122approx {frac {33,000}{2pi }}.,$

Principio de los momentos

El principio de los momentos, también conocido como teorema de Varignon (que no debe confundirse con el teorema geométrico del mismo nombre) establece que los pares resultantes debido a varias fuerzas aplicadas a un punto es igual a la suma de los pares contribuyentes:

{displaystyle tau =mathbf {r} _{1}times mathbf {F} _{1}+mathbf {r} _{2}times mathbf {F} _{2}+ldots +mathbf {r} _{N}times mathbf {F} _{N}.}

De esto se deduce que los momentos de torsión resultantes de dos fuerzas que actúan alrededor de un pivote sobre un objeto están equilibrados cuando

{displaystyle mathbf {r} _{1}times mathbf {F} _{1}+mathbf {r} _{2}times mathbf {F} _{2}=mathbf {0}.}

Multiplicador de par

El par se puede multiplicar a través de tres métodos: ubicando el fulcro de manera que aumente la longitud de una palanca; usando una palanca más larga; o mediante el uso de un juego de engranajes o caja de engranajes reductores de velocidad. Dicho mecanismo multiplica el par, ya que se reduce la velocidad de rotación.

Contenido relacionado

Más resultados...