Esfuerzo cortante

format_list_bulleted Contenido keyboard_arrow_down

ImprimirCitar

Componente de coplanar de estrés con una sección transversal material

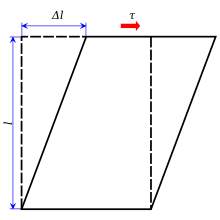
Esfuerzo cortante (a menudo indicado por $τ$ (griego: tau)) es el componente de la tensión coplanar con una sección transversal del material. Surge de la fuerza cortante, la componente del vector de fuerza paralela a la sección transversal del material. La tensión normal, por otro lado, surge de la componente del vector de fuerza perpendicular a la sección transversal del material sobre el que actúa.

Esfuerzo cortante general

La fórmula para calcular el esfuerzo cortante promedio es fuerza por unidad de área:

{displaystyle tau ={F over A},}

donde:

$τ$ = el estrés de la cizaña;
$F$ = la fuerza aplicada;
$A$ = área transversal de material con área paralela al vector de fuerza aplicado.

Otras formas

Esfuerzo cortante de la pared

Esfuerzo cortante de la pared expresa la fuerza retardadora (por unidad de área) de una pared en las capas de un fluido que fluye junto a la pared. Se define como:

{displaystyle tau _{w}:=mu left.{frac {partial u}{partial y}}right|_{y=0}}

mu

u

y

Se utiliza, por ejemplo, en la descripción del flujo sanguíneo arterial, en cuyo caso hay evidencia de que afecta el proceso aterogénico.

Pura

(feminine)Did you mean:

Pure shear stress is related to pure shear strain, denoted γ, by the following equation:

{displaystyle tau =gamma G,}

G

{displaystyle G={frac {E}{2(1+nu)}}.}

E

.

Corte de viga

El corte de una viga se define como el esfuerzo cortante interno de una viga causado por la fuerza cortante aplicada a la viga.

{displaystyle tau:={frac {fQ}{Ib}},}

donde

$f$ = total shear force at the location in question;
$Q$ = momento estadístico de la zona;
$b$ = espesor (anchura) en el material perpendicular al revestimiento;
$I$ = momento de inercia de toda la zona transversal.

La fórmula de corte de viga también se conoce como fórmula de tensión de corte de Zhuravskii en honor a Dmitrii Ivanovich Zhuravskii, quien la derivó en 1855.

Cizalla semimonocasco

Las tensiones cortantes dentro de una estructura semimonocasco se pueden calcular idealizando la sección transversal de la estructura en un conjunto de largueros (que solo soportan cargas axiales) y almas (que solo soportan flujos cortantes). Al dividir el flujo cortante por el espesor de una porción dada de la estructura semimonocasco se obtiene el esfuerzo cortante. Por lo tanto, el esfuerzo cortante máximo se producirá en la red de flujo de corte máximo o de espesor mínimo.

Las construcciones en el suelo también pueden fallar debido al corte; por ejemplo, el peso de una presa o dique lleno de tierra puede provocar el colapso del subsuelo, como un pequeño deslizamiento de tierra.

Cizallamiento por impacto

El esfuerzo cortante máximo creado en una barra redonda sólida sujeta a impacto viene dado por la ecuación:

{displaystyle tau ={sqrt {frac {2UG}{V}}},}

donde

$U$ = cambio en la energía cinética;
$G$ = módulo de esquila;
$V$ = volumen de varilla;

$U = U rotación + U aplicada$ ;
$U rotación = 1 / 2 Iω 2$ ;
$U aplicada = Tθ desplazados$ ;
$I$ = momento de masa de inercia;
$\cdot$ = velocidad angular.

Esfuerzo cortante en fluidos

Cualquier fluido real (incluidos líquidos y gases) que se mueva a lo largo de un límite sólido incurrirá en un esfuerzo cortante en ese límite. La condición de no deslizamiento dicta que la velocidad del fluido en el límite (en relación con el límite) es cero; aunque a cierta altura del límite, la velocidad del flujo debe ser igual a la del fluido. La región entre estos dos puntos se denomina capa límite. Para todos los fluidos newtonianos en flujo laminar, el esfuerzo cortante es proporcional a la tasa de deformación en el fluido, donde la viscosidad es la constante de proporcionalidad. Para los fluidos no newtonianos, la viscosidad no es constante. El esfuerzo cortante se imparte al límite como resultado de esta pérdida de velocidad.

Did you mean:

For a Newtonian fluid, the shear stress at a surface element parallel to a flat plate at the point y is given by:

{displaystyle tau (y)=mu {frac {partial u}{partial y}}}

donde

$μ$ es la viscosidad dinámica del flujo;
$u$ es la velocidad de flujo a lo largo del límite;
$Sí.$ es la altura sobre el límite.

Específicamente, el esfuerzo cortante de la pared se define como:

{displaystyle tau _{mathrm {w} }:=tau (y=0)=mu left.{frac {partial u}{partial y}}right|_{y=0}~.}

La ley constitutiva de Newton, para cualquier geometría general (incluida la placa plana mencionada anteriormente), establece que el tensor de corte (un tensor de segundo orden) es proporcional al gradiente de velocidad del flujo (la velocidad es un vector, por lo que su gradiente es un tensor de segundo orden):

{displaystyle {boldsymbol {tau }}(mathbf {u})=mu {boldsymbol {nabla }}mathbf {u} }

y la constante de proporcionalidad se denomina viscosidad dinámica. Para un flujo newtoniano isotrópico es un escalar, mientras que para flujos newtonianos anisotrópicos también puede ser un tensor de segundo orden. El aspecto fundamental es que para un fluido newtoniano la viscosidad dinámica es independiente de la velocidad del flujo (es decir, la ley constitutiva del esfuerzo cortante es lineal), mientras que para flujos no newtonianos esto no es cierto, y se debe permitir para la modificación:

{displaystyle {boldsymbol {tau }}(mathbf {u})=mu (mathbf {u}){boldsymbol {nabla }}mathbf {u} }

Esta ya no es la ley de Newton sino una identidad tensorial genérica: siempre se puede encontrar una expresión de la viscosidad en función de la velocidad del flujo dada cualquier expresión de la tensión cortante en función de la velocidad del flujo. Por otro lado, dado un esfuerzo cortante en función de la velocidad del flujo, representa un flujo newtoniano sólo si puede expresarse como una constante para el gradiente de la velocidad del flujo. La constante que se encuentra en este caso es la viscosidad dinámica del flujo.

Ejemplo

Considerando un espacio 2D en coordenadas cartesianas (x,y) (las componentes de la velocidad del flujo son respectivamente (u,v )), entonces la matriz de esfuerzos cortantes dada por:

{displaystyle {begin{pmatrix}tau _{xx}&tau _{xy}\tau _{yx}&tau _{yy}end{pmatrix}}={begin{pmatrix}x{frac {partial u}{partial x}}&0\0&-t{frac {partial v}{partial y}}end{pmatrix}}}

{displaystyle {begin{pmatrix}tau _{xx}&tau _{xy}\tau _{yx}&tau _{yy}end{pmatrix}}={begin{pmatrix}x&0\0&-tend{pmatrix}}cdot {begin{pmatrix}{frac {partial u}{partial x}}&{frac {partial u}{partial y}}\{frac {partial v}{partial x}}&{frac {partial v}{partial y}}end{pmatrix}},}

{displaystyle {begin{pmatrix}mu _{xx}&mu _{xy}\mu _{yx}&mu _{yy}end{pmatrix}}={begin{pmatrix}x&0\0&-tend{pmatrix}}}

{displaystyle {boldsymbol {mu }}(x,t)={begin{pmatrix}x&0\0&-tend{pmatrix}}}

Este flujo es, por tanto, newtoniano. Por otro lado, un flujo en el que las viscosidades fueran:

{displaystyle {begin{pmatrix}mu _{xx}&mu _{xy}\mu _{yx}&mu _{yy}end{pmatrix}}={begin{pmatrix}{frac {1}{u}}&0\0&{frac {1}{u}}end{pmatrix}}}

{displaystyle mu (u)={frac {1}{u}}}

Medición con sensores

Sensor de tensión de corte de franja divergente

Esta relación se puede aprovechar para medir el esfuerzo cortante de la pared. Si un sensor pudiera medir directamente el gradiente del perfil de velocidad en la pared, entonces multiplicarlo por la viscosidad dinámica daría como resultado el esfuerzo cortante. A. A. Naqwi y W. C. Reynolds demostraron un sensor de este tipo. El patrón de interferencia generado al enviar un haz de luz a través de dos rendijas paralelas forma una red de franjas linealmente divergentes que parecen originarse en el plano de las dos rendijas (ver experimento de la doble rendija). Cuando una partícula en un fluido pasa a través de las franjas, un receptor detecta el reflejo del patrón de franjas. La señal se puede procesar y, conociendo el ángulo marginal, se puede extrapolar la altura y la velocidad de la partícula. El valor medido del gradiente de velocidad de la pared es independiente de las propiedades del fluido y, como resultado, no requiere calibración. Los avances recientes en las tecnologías de fabricación microóptica han hecho posible el uso de elementos ópticos difractivos integrados para fabricar sensores de tensión de corte de franjas divergentes utilizables tanto en aire como en líquido.

Sensor de tensión cortante de micropilar

Otra técnica de medición es la de los delgados micropilares montados en la pared hechos del polímero flexible PDMS, que se doblan en reacción a las fuerzas de arrastre aplicadas en las proximidades de la pared. Por lo tanto, el sensor pertenece al principio de medición indirecta, que se basa en la relación entre los gradientes de velocidad cerca de la pared y la tensión de corte local en la pared.

Did you mean:

Electron-Diffusion method

El método de electrodifusión mide la velocidad de corte de la pared en la fase líquida del microelectrodo en condiciones de corriente de difusión limitante. Una diferencia de potencial entre un ánodo de superficie amplia (normalmente situado lejos del área de medición) y el pequeño electrodo de trabajo que actúa como cátodo conduce a una rápida reacción redox. La desaparición de iones se produce sólo en la superficie activa de la microsonda, provocando el desarrollo de la capa límite de difusión, en la que la rápida velocidad de reacción de electrodifusión está controlada únicamente por la difusión. La resolución de la ecuación convectiva-difusiva en la región cercana a la pared del microelectrodo conduce a soluciones analíticas que dependen de las características de longitud de las microsondas, las propiedades de difusión de la solución electroquímica y la velocidad de corte de la pared.

Contenido relacionado

Más resultados...