Esfera integradora

Una esfera integradora (también conocida como esfera de Ulbricht) es un componente óptico que consiste en una cavidad esférica hueca cuyo interior está cubierto con un revestimiento reflectante blanco difuso, con pequeños orificios para los puertos de entrada y salida. Su propiedad relevante es un efecto de dispersión o difusión uniforme. Los rayos de luz que inciden en cualquier punto de la superficie interior se distribuyen de manera uniforme a todos los demás puntos mediante múltiples reflexiones de dispersión. Los efectos de la dirección original de la luz se minimizan. Una esfera integradora puede considerarse como un difusor que conserva la potencia pero destruye la información espacial. Se utiliza normalmente con alguna fuente de luz y un detector para la medición de la potencia óptica. Un dispositivo similar es la esfera de enfoque o de Coblentz, que se diferencia en que tiene una superficie interior similar a un espejo (especular) en lugar de una superficie interior difusa.

En 1892, W. E. Sumpner publicó una expresión para el caudal de un recinto esférico con paredes que reflejan de forma difusa. Ř. Ulbricht desarrolló una realización práctica de la esfera integradora, tema de una publicación en 1900. Se ha convertido en un instrumento estándar en fotometría y radiometría y tiene la ventaja sobre un goniofotómetro de que la potencia total producida por una fuente se puede obtener en una sola medición. También se han analizado teóricamente otras formas, como una caja cúbica.

Incluso las esferas integradoras comerciales pequeñas cuestan miles de dólares, por lo que su uso suele estar limitado a la industria y a las grandes instituciones académicas. Sin embargo, la impresión 3D y los recubrimientos caseros han permitido producir esferas DIY precisas experimentalmente a un coste muy bajo.

La teoría de las esferas integradoras se basa en estos supuestos:

• La luz golpeando los lados de la esfera está dispersa de una manera difusa, es decir, la reflectancia lambertiana
• Sólo la luz que se ha difundido en la esfera golpea los puertos o detectores utilizados para probing la luz

Con estas suposiciones se puede calcular el multiplicador de esfera. Este número es el número promedio de veces que un fotón se dispersa en la esfera, antes de que sea absorbido por el revestimiento o escape a través de un puerto. Este número aumenta con la reflectividad del revestimiento de la esfera y disminuye con la relación entre el área total de los puertos y otros objetos absorbentes y el área interna de la esfera. Para obtener una alta homogeneidad, un multiplicador de esfera recomendado es 10-25.

La teoría establece además que si se cumplen los criterios anteriores, la irradiancia sobre cualquier elemento de área de la esfera será proporcional al flujo radiante total que ingresa a la esfera. Las mediciones absolutas del flujo luminoso de instancia se pueden realizar midiendo una fuente de luz conocida y determinando la función de transferencia o curva de calibración.

Para una esfera con radio r, coeficiente de reflexión ρ y flujo de fuente Φ, la irradiancia reflejada inicial es igual a:

${\displaystyle E=\rho {\frac {\fnMicrosoft Sans}\fnMicrosoft Sans Serif}$

Cada vez que se refleja la radiación, el coeficiente de reflexión crece exponencialmente. La ecuación resultante es

${\displaystyle E={\frac {}{4\pi r^{2}}\,\rho (1+\rho +\rho ^{2}+) }$

Como ρ ≤ 1, la serie geométrica converge y la irradiancia de salida total es:

${\displaystyle E={\frac}{4\pi r^{2}\,{\frac {\rho }{1-\rho }\,}$

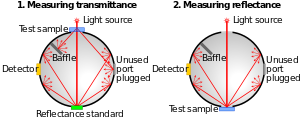
Las esferas integradoras se utilizan para diversas mediciones ópticas, fotométricas o radiométricas. Se utilizan para medir la luz total irradiada en todas las direcciones desde una lámpara. Una esfera integradora se puede utilizar para crear una fuente de luz con una intensidad aparente uniforme en todas las posiciones dentro de su apertura circular e independiente de la dirección, excepto por la función coseno inherente a las superficies radiantes idealmente difusas (superficies lambertianas). Una esfera integradora se puede utilizar para medir la reflectancia difusa de las superficies, proporcionando un promedio en todos los ángulos de iluminación y observación.

Existen varios métodos para medir la reflectancia absoluta de un objeto de prueba montado sobre una esfera integradora. En 1916, E. B. Rosa y A. H. Taylor publicaron el primer método de este tipo. Trabajos posteriores de A. H. Taylor, Frank A. Benford, C. H. Sharpe y W. F. Little, Enoch Karrer y Leonard Hanssen y Simon Kaplan ampliaron el número de métodos únicos que miden objetos de prueba montados en el puerto. Edwards et al., Korte y Schmidt y Van den Akker et al. desarrollaron métodos que miden objetos de prueba montados en el centro.

La luz dispersada por el interior de la esfera integradora se distribuye uniformemente en todos los ángulos. La esfera integradora se utiliza en mediciones ópticas. La potencia total (flujo) de una fuente de luz se puede medir sin imprecisiones causadas por las características direccionales de la fuente o del dispositivo de medición. Se puede estudiar la reflexión y la absorción de las muestras. La esfera crea una fuente de radiación de referencia que se puede utilizar para proporcionar un estándar fotométrico.

Dado que se recoge toda la luz que incide en el puerto de entrada, un detector conectado a una esfera integradora puede medir con precisión la suma de toda la luz ambiental que incide en una pequeña abertura circular. Se puede medir la potencia total de un rayo láser, sin tener en cuenta los efectos de la forma del rayo, la dirección y la posición de incidencia, así como la polarización.

Las propiedades ópticas del revestimiento de la esfera afectan en gran medida a su precisión. Se deben utilizar diferentes revestimientos en longitudes de onda visibles, infrarrojas y ultravioleta. Las fuentes de iluminación de alta potencia pueden calentar o dañar el revestimiento, por lo que una esfera integradora se evaluará para un nivel máximo de potencia incidente. Se utilizan varios materiales de revestimiento. Para la luz del espectro visible, los primeros experimentadores utilizaron un depósito de óxido de magnesio, y el sulfato de bario también tiene una reflectancia plana útil en el espectro visible. También se utilizan varios compuestos de PTFE patentados para mediciones de luz visible. Se utiliza oro finamente depositado para mediciones infrarrojas.

Un requisito importante para el material de recubrimiento es la ausencia de fluorescencia. Los materiales fluorescentes absorben luz de longitud de onda corta y reemiten luz en longitudes de onda más largas. Debido a las numerosas dispersiones, este efecto es mucho más pronunciado en una esfera integradora que en los materiales irradiados de forma normal.

La teoría de la esfera integradora supone una superficie interior uniforme con una reflectividad difusa cercana al 100%. Las aberturas por donde puede entrar o salir la luz, utilizadas para detectores y fuentes, normalmente se denominan puertos. El área total de todos los puertos debe ser pequeña, inferior al 5% de la superficie de la esfera, para que las suposiciones teóricas sean válidas. Por lo tanto, los puertos no utilizados deben tener tapones correspondientes, con la superficie interior del tapón recubierta con el mismo material que el resto de la esfera.

Las esferas integradoras varían en tamaño desde unos pocos centímetros de diámetro hasta unos pocos metros de diámetro. Las esferas más pequeñas se utilizan normalmente para difundir la radiación entrante, mientras que las esferas más grandes se utilizan para medir propiedades integradoras como el flujo luminoso de una lámpara o luminarias que luego se colocan dentro de la esfera.

Si la luz que entra es incoherente (en lugar de un rayo láser), entonces normalmente llena el puerto de origen y la relación entre el área del puerto de origen y el área del puerto del detector es relevante.

Normalmente se insertan deflectores en la esfera para bloquear el paso directo de la luz desde un puerto de fuente a un puerto de detector, ya que esta luz tendrá una distribución no uniforme.

• Lambert's cosine law

• RP Photonics, Enciclopedia de Física y Tecnología láser, Integración de esferas
• Pike Technologies, Integración de Esferas – Introducción y Teoría, Nota de Aplicación de Tecnologías de Pike
• Newport, Flange Mount Integrating Spheres
• Whitehead, Lorne A.; Mossman, Michele A. (2006). "Jack O'Lanterns e integrar esferas: Física de Halloween". Diario Americano de Física. 74 (6): 537-541. Código:2006AmJPh..74..537W. doi:10.1119/1.2190687.
• Ducharme, Alfred; Daniels, Arnold; Grann, Eric; Boreman, Glenn (1997). "Design of an Integrating Sphere as a Uniform Illumination Source". Transacciones IEEE en Educación. 40 (2): 131–134. Bibcode:1997ITEdu..40..131D. doi:10.1109/13.572326. S2CID 61946451.
• Peter Hiscocks, la integración de la esfera para la calibración de la luminosidad Archived 2012-01-06 en la máquina Wayback, Rev 6, mayo 2016
• Ci Systems, integración de la introducción de la esfera, estructura mecánica, calibración y fuentes
• Electro-Optical Industries, Integrating Spheres
• Situación de la integración de la esfera en China