Esfera de fotones

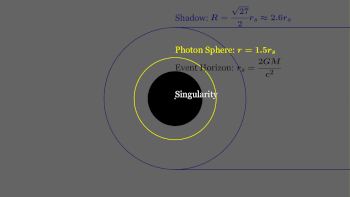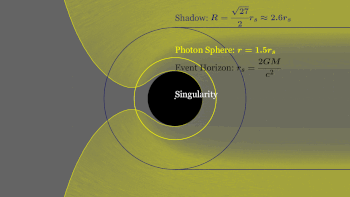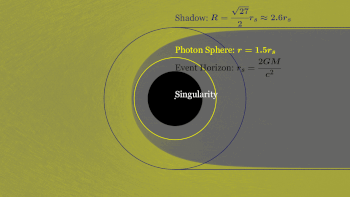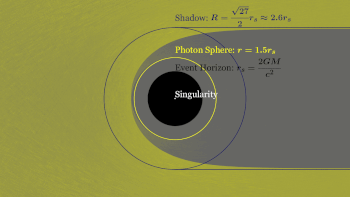
Una esfera de fotones o un círculo de fotones es un área o región del espacio donde la gravedad es tan fuerte que los fotones se ven obligados a viajar en órbitas, lo que a veces también se llama última órbita del fotón. El radio de la esfera de fotones, que también es el límite inferior de cualquier órbita estable, es, para un agujero negro de Schwarzschild,

r=3GMc2=3rs2,{displaystyle r={frac {3GM}{c^{2}={frac} {3r_{text{s}} {2}}}}} {3r_{f}} {f}} {f}}}}} {c}}}}}} {f}}} {f}}}}} {f}}} {f}}}}}}}}}}} {f}}}}

donde G es la constante gravitacional, M es la masa del agujero negro, c es la velocidad de la luz en el vacío y r_s es el radio de Schwarzschild (el radio del horizonte de sucesos); consulte a continuación una derivación de este resultado.

Esta ecuación implica que las esferas de fotones sólo pueden existir en el espacio que rodea a un objeto extremadamente compacto (un agujero negro o posiblemente una estrella de neutrones "ultracompacta").

La esfera de fotones se encuentra más lejos del centro de un agujero negro que el horizonte de sucesos. Dentro de una esfera de fotones, es posible imaginar un fotón que se emite (o refleja) desde la parte posterior de la cabeza y, siguiendo una órbita del agujero negro, luego es interceptado por el ojo de la persona. , permitiendo ver la parte posterior de la cabeza. Para los agujeros negros no giratorios, la esfera de fotones es una esfera de radio 3/2 r_s. No existen órbitas estables de caída libre que existan dentro o que crucen la esfera de fotones. Cualquier órbita en caída libre que la cruce desde el exterior gira en espiral hacia el agujero negro. Cualquier órbita que lo atraviese desde el interior escapa al infinito o vuelve a caer y gira en espiral hacia el agujero negro. No es posible una órbita no acelerada con un semieje mayor menor que esta distancia, pero dentro de la esfera de fotones, una aceleración constante permitirá que una nave espacial o una sonda flote sobre el horizonte de sucesos.

Otra propiedad de la esfera de fotones es la inversión de la fuerza centrífuga (nota: no centrípeta). Fuera de la esfera de fotones, cuanto más rápido se orbita, mayor es la fuerza hacia afuera que se siente. La fuerza centrífuga cae a cero en la esfera de fotones, incluidas las órbitas sin caída libre a cualquier velocidad, es decir, un objeto pesa lo mismo sin importar qué tan rápido orbite y se vuelve negativo dentro de él. Dentro de la esfera de fotones, una órbita más rápida conduce a un mayor peso o fuerza hacia adentro. Esto tiene serias ramificaciones para la dinámica de fluidos del flujo de fluido entrante.

Un agujero negro en rotación tiene dos esferas de fotones. Cuando un agujero negro gira, arrastra el espacio consigo. La esfera de fotones que está más cerca del agujero negro se mueve en la misma dirección que la rotación, mientras que la esfera de fotones más alejada se mueve en contra de él. Cuanto mayor es la velocidad angular de rotación de un agujero negro, mayor es la distancia entre las dos esferas de fotones. Dado que el agujero negro tiene un eje de rotación, esto sólo es cierto si nos acercamos al agujero negro en la dirección del ecuador. En una órbita polar sólo hay una esfera de fotones. Esto se debe a que al acercarse en este ángulo no existe la posibilidad de viajar a favor o en contra de la rotación. En cambio, la rotación hará que la órbita precese.

Derivación de un agujero negro de Schwarzschild

Dado que un agujero negro de Schwarzschild tiene simetría esférica, todos los ejes posibles para una órbita circular de un fotón son equivalentes y todas las órbitas circulares tienen el mismo radio.

Esta derivación implica el uso de la métrica de Schwarzschild, dada por

ds2=()1− − rsr)c2dt2− − ()1− − rsr)− − 1dr2− − r2()pecado2⁡ ⁡ Silencio Silencio dφ φ 2+dSilencio Silencio 2).{displaystyle ¿Por qué? {r_{text{2} {r}}}right)}{-1},dr^{2}-r^{2}(sin ^{2}theta ,dphi ^{2}+dtheta ^{2}). }

Para un fotón viajando a un radio constante r (es decir, en el φ- dirección coordinada), dr=0{displaystyle dr=0}. Ya que es un fotón, ds=0{displaystyle ds=0} (un "intervalo similar a la luz"). Siempre podemos girar el sistema de coordenadas de tal manera que Silencio Silencio {displaystyle theta } es constante, dSilencio Silencio =0{displaystyle dtheta =0} (por ejemplo, Silencio Silencio =π π /2{displaystyle theta =pi}).

Estableciendo ds, dr y dθ en cero, tenemos

()1− − rsr)c2dt2=r2pecado2⁡ ⁡ Silencio Silencio dφ φ 2.{displaystyle left(1-{frac {text{s}}{r}right)c^{2},dt^{2}=r^{2}sin ^{2}theta ,dphi ^{2}}

Reorganizar las donaciones

dφ φ dt=crpecado⁡ ⁡ Silencio Silencio 1− − rsr.{displaystyle {frac {fnMicroc}dphi } {dt}={frac {c}{rsin theta }{sqrt {1-{frac {}}}}}

Para proceder, necesitamos la relación dφ φ dt{displaystyle {frac {fnMicroc}dphi } {dt}}. Para encontrarlo, utilizamos la ecuación geodésica radial

d2rdτ τ 2+. . μ μ . . ruμ μ u. . =0.{fnMicroc {fnMicrosoft} {fnMicrosoft} {fnMicrosoft} {f}} {f}}}} {fn}} {fnK}}} {fnMicrosoft}}} {f}}}}}}}}}} {fnK}}}}} {f} . Gamma... - Sí.

No desaparecer . . {displaystyle "Gamma"- Los coeficientes de conexión son

. . ttr=c2BB.2,. . rrr=− − B− − 1B.2,. . Silencio Silencio Silencio Silencio r=− − rB,. . φ φ φ φ r=− − Brpecado2⁡ ⁡ Silencio Silencio ,{displaystyle #Gamma _{ttt}={frac {c^{2}{2}}quad Gamma _{rr}{r}=-{frac} {B^{-1}B}{2}}}quad Gamma _{theta theta } {r}=-rB,quad Gamma _{2}theta}

Donde B.=dBdr, B=1− − rsr{displaystyle B'={frac {dB}} B=1-{frac} {fnK}} {fnK}}} {fn}}}}} {f}}}}}} {f}}}}} {f}}}} {f}}}}}} {f}}}} {f}}}}}} {}}}}}}}}}} {}}}}}}}} {}}}}}}} {}}}}}}}}}}}}}}} {}}}}}}}}}}}}}}}}}}}}}} {}}}}}}}}}}}}}}}}}}}}} {}}}}}}}}}}}}}}}}}} {}}}}}}}}}}}}}}}}}}}} {}}}}}}}}}}}}}}}}}}}}}}}} {}}}}}}}}}}}}}}}}}}}}}}}}}}}}.

Tratamos la geodesia radial fotones con constante r y Silencio Silencio {displaystyle theta }, por consiguiente

drdτ τ =d2rdτ τ 2=dSilencio Silencio dτ τ =0.{displaystyle {frac {}{dtau {fnK}} {fnMicroc {fnK}} {f}} {fnK}}} {fn}} {fn}}} {fn}}}}} {fn}}}} {fn} {f}}}}} {f} {fnfnf} {fnf}f}f}f}f}f}f}f}f}f}f}f}f}f}f}f}f}f}f}fn}f}fnf}f}f}f}f}f}f}fnf}fnfn}f}f}f}fnfnf}f}fnfnfn}fnfnf}fnf}f}fn}f}fn} ¿Qué? - Sí.

Sustituyendo todo esto en la ecuación geodésica radial (la ecuación geodésica con la coordenada radial como variable dependiente), obtenemos

()dφ φ dt)2=c2rs2r3pecado2⁡ ⁡ Silencio Silencio .{displaystyle left({frac {dphi }{dt}right)^{2}={frac} {c^{2}r_{text{s}}{2r^{3}sin ^{2}theta }}

Comparándolo con lo obtenido anteriormente, tenemos

crs2r=c1− − rsr,{fnMicroc} {fnMicrosoft}} {fnK}} {fnMicrosoft}} {f}}} {f}}} {f}}} {fn}}}} {f}}} {f}}}} {f}}}}}} {c{f}}}}} {f}}}}}}} {c{f}}}}}}}}}}}}}}} {c{c{f}}}}}}}}}}}}}}}}}}} {c{c{f}}}}}}}}}}}}}}}}}}}}}}}}}}} {c{c{c{f}}}}}}}}}}}}}}}}}}}}}}}}}}}}}} {c{c{c{c{c{c{c{c{c{f}}}}} {1-{frac {}}}}

donde hemos insertado Silencio Silencio =π π /2{displaystyle theta =pi} radians (imagina que la masa central, sobre la que está orbitando el fotón, se encuentra en el centro de los ejes de coordenadas. Entonces, como el foton viaja a lo largo del φ φ {displaystyle phi }- línea coordinada, para que la masa se encuentre directamente en el centro de la órbita del fotono, debemos tener Silencio Silencio =π π /2{displaystyle theta =pi} radians).

Por lo tanto, reorganizar esta expresión final da

r=32rs,{displaystyle r={frac {3} {2}r_{text{s}}}

cuál es el resultado que nos propusimos demostrar.

El fotón orbita alrededor de un agujero negro de Kerr

A diferencia de un agujero negro de Schwarzschild, un agujero negro de Kerr (giratorio) no tiene simetría esférica, sino sólo un eje de simetría, lo que tiene profundas consecuencias para las órbitas de los fotones, ver p.e. Cramer para obtener detalles y simulaciones de órbitas y círculos de fotones. Hay dos órbitas circulares de fotones en el plano ecuatorial (prograda y retrógrada), con diferentes radios de Boyer-Lindquist:

r± ± ∘ ∘ =rs[1+#⁡ ⁡ ()23Arccos⁡ ⁡ ± ± SilencioaSilencioM)],{displaystyle . ¿Qué?

Donde a=J/M{displaystyle a=J/M} es el impulso angular por unidad de masa del agujero negro. Existen otras órbitas constantes-radius, pero tienen caminos más complicados que oscilan en la latitud sobre el Ecuador.