Escala logarítmica
a escala logarítmica (o escala de registro ) es una forma de mostrar datos numéricos en un rango muy amplio de valores de manera compacta. A diferencia de una línea numérica lineal en la que cada unidad de distancia corresponde a agregar en la misma cantidad, en una escala logarítmica, cada unidad de longitud corresponde a multiplicar el valor anterior en la misma cantidad. Por lo tanto, dicha escala no es lineal: los números 1, 2, 3, 4, 5, y así sucesivamente, no están igualmente espaciados. Más bien, los números 10, 100, 1000, 10000 y 100000 estarían igualmente espaciados. Del mismo modo, los números 2, 4, 8, 16, 32, y así sucesivamente, estarían igualmente espaciados. A menudo, las curvas de crecimiento exponencial se muestran en una escala de registro, de lo contrario, aumentarían demasiado rápido para encajar dentro de un pequeño gráfico.
usos comunes
Las marcas en las reglas de diapositivas se organizan en una escala de registro para multiplicar o dividir números sumando o restando longitudes en las escalas.
Los siguientes son ejemplos de escalas logarítmicas de uso común, donde una cantidad mayor da como resultado un valor más alto:
- Escala de magnitud y escala de magnitud de momento (MMS) para la fuerza de terremotos y movimientos en la Tierra
- Nivel de sonido, con unidades decibel
- Neper para amplitud, campo y cantidades de potencia
- Nivel de frecuencia, con unidades cent, menor segundo, mayor segundo, y octava para el lanzamiento relativo de notas en la música
- Logit for odds in statistics
- Escala de peligros de impacto técnico de Palermo
- Línea de tiempo logarítmica
- Contando f-stops para ratios de exposición fotográfica
- La regla de los nueve utilizados para la calificación de baja probabilidad
- Entropía en termodinámica
- Información en teoría de la información
- Curvas de distribución del tamaño de las partículas del suelo
Los siguientes son ejemplos de escalas logarítmicas de uso común, donde una cantidad mayor da como resultado un valor más bajo (o negativo):
- p H para la acidez
- Escala de magnitud estelar para el brillo de las estrellas
- Escala de Krumbein para el tamaño de partículas en geología
- Absorbancia de luz por muestras transparentes
Algunos de nuestros sentidos funcionan de manera logarítmica (ley de Weber-Fechner), lo que hace que las escalas logarítmicas para estas cantidades de entrada sean especialmente apropiadas. En particular, nuestro sentido del oído percibe proporciones iguales de frecuencias como diferencias iguales en el tono. Además, los estudios de niños pequeños en una tribu aislada han demostrado que las escalas logarítmicas son la representación numérica más natural en algunas culturas.
Representación gráfica
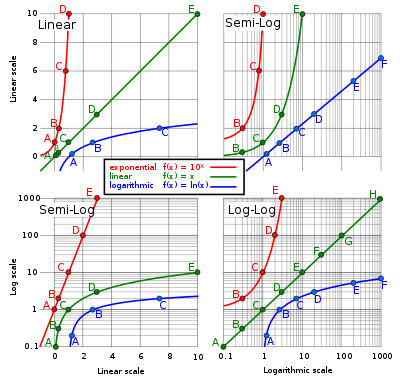
El gráfico superior izquierdo es lineal en los ejes X e Y, y el eje Y varía de 0 a 10. Se usa una escala logarítmica de base 10 para el eje Y del gráfico inferior izquierdo, y el eje Y varía de 0,1 a 1.000.
El gráfico superior derecho usa una escala log-10 solo para el eje X, y el gráfico inferior derecho usa una escala log-10 tanto para el eje X como para el eje Y.
La presentación de datos en una escala logarítmica puede ser útil cuando los datos:
- cubre una amplia gama de valores, ya que el uso de los logaritmos de los valores en lugar de los valores reales reduce una amplia gama a un tamaño más manejable;
- puede contener leyes exponenciales o leyes de poder, ya que éstas aparecerán como líneas rectas.
Una regla de cálculo tiene escalas logarítmicas y los nomogramas suelen emplear escalas logarítmicas. La media geométrica de dos números está a medio camino entre los números. Antes de la llegada de los gráficos por computadora, el papel cuadriculado logarítmico era una herramienta científica de uso común.
Gráficas logarítmicas
Si tanto el eje vertical como el horizontal de una gráfica se escalan logarítmicamente, la gráfica se denomina gráfica logarítmica.
Gráficas semilogarítmicas
Si solo la ordenada o la abscisa se escalan logarítmicamente, el gráfico se denomina gráfico semilogarítmico.
Extensiones
Se puede definir una transformación logarítmica modificada para entrada negativa (y<0) y para evitar la singularidad para entrada cero (y=0) para producir parcelas logarítmicas simétricas:
- Y=Sgn ()Sí.)⋅ ⋅ log10 ()1+SilencioSí./CSilencio){displaystyle Y=operatorname {sgn}(y)cdot log _{10}(1+ torturay/C sometida)}
para una constante C=1/ln(10).
Unidades logarítmicas
Una unidad logarítmica es una unidad que se puede utilizar para expresar una cantidad (física o matemática) en una escala logarítmica, es decir, como proporcional al valor de una función logarítmica aplicada a la relación entre la cantidad y una cantidad de referencia del mismo tipo. La elección de la unidad generalmente indica el tipo de cantidad y la base del logaritmo.
Ejemplos
Ejemplos de unidades logarítmicas incluyen unidades de capacidad de almacenamiento de datos (bit, byte), de información y entropía de información (nat, shannon, ban) y de nivel de señal (decibel, bel, neper). Las cantidades de frecuencia logarítmica se utilizan en electrónica (década, octava) y para intervalos de tono de música (octava, semitono, centésima, etc.). Otras unidades de escala logarítmica incluyen el punto de escala de magnitud de Richter.
Además, varias medidas industriales son logarítmicas, como los valores estándar de las resistencias, el calibre de alambre estadounidense, el calibre de Birmingham utilizado para alambre y agujas, etc.
Unidades de información
- Bit, byte
- Hartley
- Nat
- Shannon
Unidades de nivel o diferencia de nivel
- bel, decibel
- neper
Unidades de intervalo de frecuencia
- decadencia, decisióncade, savart
- octave, tono, semitona, cent
Tabla de ejemplos
| Dependencia | Base de logaritmo | Cantidad subyacente | Interpretación |
|---|---|---|---|
| bit | 2 | número de mensajes posibles | cantidad de información |
| byte | 28 = 256 | número de mensajes posibles | cantidad de información |
| decibel | 10(1/10) Entendido 1.259 | cualquier cantidad de potencia (poder de sonido, por ejemplo) | nivel de potencia de sonido (por ejemplo) |
| decibel | 10(1/20) Entendido 1.122 | cualquier cantidad de poder raíz (presión de sonido, por ejemplo) | nivel de presión de sonido (por ejemplo) |
| semitone | 2(1/12) Entendido 1.059 | frecuencia de sonido | intervalo de lanzamiento |
Las dos definiciones de decibelio son equivalentes, porque una relación de cantidades de potencia es igual al cuadrado de la relación correspondiente de cantidades de potencia raíz.
Contenido relacionado
Gomoku
Complejidad de Kolmogorov
Función multiplicativa