Entrelazamiento cuántico

El proceso de conversión paramétrica espontánea puede dividir fotones en pares fotones tipo II con polarización mutuamente perpendicular.

Entrelazamiento cuántico es el fenómeno que ocurre cuando un grupo de partículas se genera, interactúa o comparte proximidad espacial de tal manera que el estado cuántico de cada partícula del grupo no puede describirse independientemente de el estado de los demás, incluso cuando las partículas están separadas por una gran distancia. El tema del entrelazamiento cuántico está en el centro de la disparidad entre la física clásica y la cuántica: el entrelazamiento es una característica principal de la mecánica cuántica que no está presente en la mecánica clásica.

Las mediciones de propiedades físicas como la posición, el momento, el espín y la polarización realizadas en partículas entrelazadas pueden, en algunos casos, estar perfectamente correlacionadas. Por ejemplo, si se genera un par de partículas entrelazadas de manera que se sabe que su espín total es cero, y se encuentra que una partícula tiene un espín en el sentido de las agujas del reloj en un primer eje, entonces el espín de la otra partícula, medido en el mismo eje, se encuentra en sentido antihorario. Sin embargo, este comportamiento da lugar a efectos aparentemente paradójicos: cualquier medición de las propiedades de una partícula da como resultado un colapso irreversible de la función de onda de esa partícula y cambia el estado cuántico original. Con partículas entrelazadas, tales mediciones afectan al sistema entrelazado como un todo.

Tales fenómenos fueron el tema de un artículo de 1935 de Albert Einstein, Boris Podolsky y Nathan Rosen, y varios artículos de Erwin Schrödinger poco después, que describían lo que se conoció como la paradoja EPR. Einstein y otros consideraron imposible tal comportamiento, ya que violaba la visión del realismo local de la causalidad (Einstein se refirió a él como "acción espeluznante a distancia") y argumentó que, por lo tanto, la formulación aceptada de la mecánica cuántica debe ser incompleta.

Más tarde, sin embargo, las predicciones contrarias a la intuición de la mecánica cuántica se verificaron en pruebas en las que se midió la polarización o el espín de partículas entrelazadas en ubicaciones separadas, violando estadísticamente la desigualdad de Bell. En pruebas anteriores, no se podía descartar que el resultado en un punto pudiera haberse transmitido sutilmente al punto remoto, afectando el resultado en la segunda ubicación. Sin embargo, el llamado "libre de lagunas legales" Se realizaron pruebas de campana donde las ubicaciones estaban lo suficientemente separadas como para que las comunicaciones a la velocidad de la luz hubieran tomado más tiempo (en un caso, 10 000 veces más) que el intervalo entre las mediciones.

Según algunas interpretaciones de la mecánica cuántica, el efecto de una medición ocurre instantáneamente. Otras interpretaciones que no reconocen el colapso de la función de onda disputan que haya algún "efecto" en absoluto. Sin embargo, todas las interpretaciones coinciden en que el entrelazamiento produce una correlación entre las medidas y que la información mutua entre las partículas entrelazadas puede explotarse, pero que cualquier transmisión de información a velocidades superiores a la de la luz es imposible.

El entrelazamiento cuántico se ha demostrado experimentalmente con fotones, neutrinos, electrones, moléculas del tamaño de bolas de Bucky e incluso pequeños diamantes. La utilización del entrelazamiento en comunicación, computación y radar cuántico es un área muy activa de investigación y desarrollo.

A pesar de la creencia popular de lo contrario, el entrelazamiento cuántico no se puede utilizar para comunicaciones más rápidas que la luz.

Historia

Título del artículo sobre el papel paradoja de Einstein-Podolsky-Rosen (EPR), en el número 4 de mayo de 1935 El New York Times.

En 1935, Albert Einstein, Boris Podolsky y Nathan Rosen publicaron un artículo sobre las predicciones contrarias a la intuición que hace la mecánica cuántica para pares de objetos preparados juntos de una manera particular. En este estudio, los tres formularon la paradoja de Einstein-Podolsky-Rosen (paradoja EPR), un experimento mental que intentaba demostrar que "la descripción mecánica cuántica de la realidad física dada por las funciones de onda no es completa".; Sin embargo, los tres científicos no acuñaron la palabra entrelazamiento, ni generalizaron las propiedades especiales del estado cuántico que consideraban. Después del artículo de EPR, Erwin Schrödinger escribió una carta a Einstein en alemán en la que usó la palabra Verschränkung (traducida por él mismo como entrelazamiento) "para describir las correlaciones entre dos partículas que interactúan y luego se separan, como en el experimento EPR."

Poco después, Schrödinger publicó un artículo seminal que definía y discutía la noción de "enredo". En el artículo, reconoció la importancia del concepto y afirmó: "Yo no llamaría [al entrelazamiento] uno sino el rasgo característico de la mecánica cuántica, el que impone su total alejamiento de las líneas clásicas de pensamiento." Al igual que Einstein, Schrödinger no estaba satisfecho con el concepto de entrelazamiento, porque parecía violar el límite de velocidad en la transmisión de información implícito en la teoría de la relatividad. Más tarde, Einstein ridiculizó el entrelazamiento como "spukhafte Fernwirkung" o "acción espeluznante a distancia".

El artículo de EPR generó un gran interés entre los físicos, lo que inspiró mucho debate sobre los fundamentos de la mecánica cuántica (quizás la interpretación más famosa de la mecánica cuántica de Bohm), pero produjo relativamente pocos otros trabajos publicados. A pesar del interés, el punto débil del argumento de EPR no se descubrió hasta 1964, cuando John Stewart Bell demostró que uno de sus supuestos clave, el principio de localidad, aplicado al tipo de interpretación de variables ocultas que esperaba EPR, era matemáticamente inconsistente con las predicciones de la teoría cuántica.

Específicamente, Bell demostró un límite superior, visto en la desigualdad de Bell, con respecto a la fuerza de las correlaciones que se pueden producir en cualquier teoría que obedezca al realismo local, y mostró que la teoría cuántica predice violaciones de este límite para ciertos sistemas entrelazados.. Su desigualdad es comprobable experimentalmente, y ha habido numerosos experimentos relevantes, comenzando con el trabajo pionero de Stuart Freedman y John Clauser en 1972 y los experimentos de Alain Aspect en 1982. Carl Kocher, quien ya en 1967 presentó un aparato en el que se mostraba que dos fotones emitidos sucesivamente por un átomo de calcio estaban entrelazados, el primer caso de luz visible entrelazada. Los dos fotones pasaron polarizadores paralelos colocados diametralmente con mayor probabilidad de lo previsto clásicamente, pero con correlaciones en concordancia cuantitativa con los cálculos de la mecánica cuántica. También mostró que la correlación variaba como el coseno cuadrado del ángulo entre los ajustes del polarizador y disminuía exponencialmente con el tiempo de retraso entre los fotones emitidos. El aparato de Kocher, equipado con mejores polarizadores, fue utilizado por Freedman y Clauser, quienes pudieron confirmar la dependencia del coseno cuadrado y usarla para demostrar una violación de la desigualdad de Bell para un conjunto de ángulos fijos. Todos estos experimentos han mostrado concordancia con la mecánica cuántica más que con el principio del realismo local.

Durante décadas, cada uno había dejado abierta al menos una escapatoria por la cual era posible cuestionar la validez de los resultados. Sin embargo, en 2015 se realizó un experimento que cerró simultáneamente las lagunas de detección y localidad, y fue anunciado como "libre de lagunas"; este experimento descartó con certeza una gran clase de teorías del realismo local. Aspect escribe que "... no se puede decir que ningún experimento... esté totalmente libre de lagunas jurídicas" pero dice que los experimentos "eliminan las últimas dudas a las que debemos renunciar" variables ocultas locales, y se refiere a ejemplos de lagunas que quedan como "descabellados" y "ajena a la forma habitual de razonar en física."

El trabajo de Bell planteó la posibilidad de utilizar estas correlaciones superfuertes como recurso para la comunicación. Condujo al descubrimiento en 1984 de los protocolos de distribución de claves cuánticas, el más famoso BB84 de Charles H. Bennett y Gilles Brassard y E91 de Artur Ekert. Aunque BB84 no usa entrelazamiento, el protocolo de Ekert usa la violación de la desigualdad de Bell como prueba de seguridad.

En 2022, el Premio Nobel de Física fue otorgado a Aspect, Clauser y Anton Zeilinger "por experimentos con fotones entrelazados, estableciendo la violación de las desigualdades de Bell y siendo pioneros en la ciencia de la información cuántica".

Concepto

Significado de enredo

Un sistema entrelazado se define como aquel cuyo estado cuántico no se puede factorizar como producto de los estados de sus constituyentes locales; es decir, no son partículas individuales sino un todo inseparable. En el entrelazamiento, un constituyente no puede describirse completamente sin considerar los otros. El estado de un sistema compuesto siempre es expresable como una suma, o superposición, de productos de estados de constituyentes locales; está enredado si esta suma no se puede escribir como un solo término de producto.

Los sistemas cuánticos pueden enredarse a través de varios tipos de interacciones. Para conocer algunas formas en que se puede lograr el entrelazamiento con fines experimentales, consulte la sección a continuación sobre métodos. El enredo se rompe cuando las partículas entrelazadas se separan a través de la interacción con el medio ambiente; por ejemplo, cuando se realiza una medición.

Como ejemplo de entrelazamiento: una partícula subatómica se descompone en un par entrelazado de otras partículas. Los eventos de decaimiento obedecen a las diversas leyes de conservación y, como resultado, los resultados de la medición de una partícula hija deben estar altamente correlacionados con los resultados de la medición de la otra partícula hija (para que los momentos totales, los momentos angulares, la energía, etc. permanezcan aproximadamente lo mismo antes y después de este proceso). Por ejemplo, una partícula de espín cero podría decaer en un par de partículas de espín 1/2. Dado que el giro total antes y después de este decaimiento debe ser cero (conservación del momento angular), cada vez que se mide que la primera partícula gira hacia arriba en algún eje, la otra, cuando se mide en el mismo eje, siempre se encuentra girando hacia abajo.. (Esto se llama el caso anticorrelacionado de espín; y si las probabilidades previas para medir cada espín son iguales, se dice que el par está en el estado singulete).

El resultado anterior puede o no ser percibido como sorprendente. Un sistema clásico mostraría la misma propiedad, y ciertamente se requeriría una teoría de variables ocultas para hacerlo, basada en la conservación del momento angular tanto en la mecánica clásica como en la cuántica. La diferencia es que un sistema clásico tiene valores definidos para todos los observables todo el tiempo, mientras que el sistema cuántico no los tiene. En un sentido que se discutirá más adelante, el sistema cuántico considerado aquí parece adquirir una distribución de probabilidad para el resultado de una medición del espín a lo largo de cualquier eje de la otra partícula al medir la primera partícula. Esta distribución de probabilidad es en general diferente de lo que sería sin la medición de la primera partícula. Esto ciertamente puede percibirse como sorprendente en el caso de partículas entrelazadas separadas espacialmente.

Paradoja

La paradoja es que una medición realizada en cualquiera de las partículas aparentemente colapsa el estado de todo el sistema entrelazado, y lo hace instantáneamente, antes de que cualquier información sobre el resultado de la medición pudiera haberse comunicado a la otra partícula (suponiendo que la información no pueda viajar más rápido que la luz) y por lo tanto aseguró el "adecuado" resultado de la medición de la otra parte del par entrelazado. En la interpretación de Copenhague, el resultado de una medición de espín en una de las partículas es un colapso en un estado en el que cada partícula tiene un espín definido (ya sea hacia arriba o hacia abajo) a lo largo del eje de medición. El resultado se considera aleatorio, con cada posibilidad con una probabilidad del 50%. Sin embargo, si ambos giros se miden a lo largo del mismo eje, se encuentra que están anticorrelacionados. Esto significa que el resultado aleatorio de la medición realizada en una partícula parece haberse transmitido a la otra, para que pueda tomar la 'elección correcta'. cuando también se mide.

La distancia y el momento de las mediciones se pueden elegir para que el intervalo entre las dos mediciones sea similar al espacio, por lo tanto, cualquier efecto causal que conecte los eventos tendría que viajar más rápido que la luz. De acuerdo con los principios de la relatividad especial, no es posible que ninguna información viaje entre dos eventos de medición de este tipo. Ni siquiera es posible decir cuál de las medidas vino primero. Para dos eventos separados en forma de espacio x₁ y x ₂ hay marcos inerciales en los que x₁ es primero y otros en el que x₂ es el primero. Por lo tanto, la correlación entre las dos medidas no puede explicarse como si una medida determinara a la otra: diferentes observadores estarían en desacuerdo sobre el papel de la causa y el efecto.

(De hecho, pueden surgir paradojas similares incluso sin entrelazamiento: la posición de una sola partícula se extiende por el espacio, y dos detectores muy separados que intentan detectar la partícula en dos lugares diferentes deben alcanzar instantáneamente la correlación adecuada, de modo que no lo hagan. ambos no detectan la partícula.)

Teoría de las variables ocultas

Una posible solución a la paradoja es suponer que la teoría cuántica es incompleta y que el resultado de las mediciones depende de "variables ocultas" predeterminadas. El estado de las partículas que se están midiendo contiene algunas variables ocultas, cuyos valores determinan efectivamente, desde el momento de la separación, cuáles serán los resultados de las mediciones de espín. Esto significaría que cada partícula lleva consigo toda la información requerida, y no es necesario transmitir nada de una partícula a la otra en el momento de la medición. Einstein y otros (ver la sección anterior) originalmente creían que esta era la única forma de salir de la paradoja, y la descripción mecánica cuántica aceptada (con un resultado de medición aleatorio) debe ser incompleta.

Violaciones de la desigualdad de Bell

Las teorías de variables ocultas locales fallan, sin embargo, cuando se consideran las mediciones del giro de partículas entrelazadas a lo largo de diferentes ejes. Si se realiza una gran cantidad de pares de tales mediciones (en una gran cantidad de pares de partículas entrelazadas), entonces, estadísticamente, si la vista de variables ocultas o realista local fuera correcta, los resultados siempre satisfarían la desigualdad de Bell. Varios experimentos han demostrado en la práctica que la desigualdad de Bell no se cumple. Sin embargo, antes de 2015, todos estos tenían problemas de lagunas que la comunidad de físicos consideraba los más importantes. Cuando las mediciones de las partículas entrelazadas se realizan en marcos de referencia relativistas en movimiento, en los que cada medición (en su propio marco de tiempo relativista) ocurre antes que la otra, los resultados de la medición permanecen correlacionados.

El problema fundamental de medir el giro a lo largo de diferentes ejes es que estas medidas no pueden tener valores definidos al mismo tiempo, son incompatibles en el sentido de que estas medidas' la máxima precisión simultánea está limitada por el principio de incertidumbre. Esto es contrario a lo que se encuentra en la física clásica, donde cualquier número de propiedades puede medirse simultáneamente con una precisión arbitraria. Se ha demostrado matemáticamente que las medidas compatibles no pueden mostrar correlaciones que violen la desigualdad de Bell y, por lo tanto, el entrelazamiento es un fenómeno fundamentalmente no clásico.

Resultados experimentales notables que prueban el entrelazamiento cuántico

El primer experimento que verificó la acción espeluznante a distancia de Einstein o el enredo fue corroborado con éxito en un laboratorio por Chien-Shiung Wu y un colega llamado I. Shaknov en 1949, y fue publicado el día de año nuevo de 1950. El resultado probó específicamente las correlaciones cuánticas de un par de fotones. En experimentos de 2012 y 2013, se creó una correlación de polarización entre fotones que nunca coexistieron en el tiempo. Los autores afirmaron que este resultado se logró mediante el intercambio de entrelazamiento entre dos pares de fotones entrelazados después de medir la polarización de un fotón del par temprano, y que demuestra que la no localidad cuántica se aplica no solo al espacio sino también al tiempo.

En tres experimentos independientes en 2013, se demostró que los estados cuánticos separables comunicados de forma clásica se pueden usar para transmitir estados entrelazados. Ronald Hanson, de la Universidad Tecnológica de Delft, llevó a cabo la primera prueba de Bell sin lagunas en 2015, lo que confirmó la violación de la desigualdad de Bell.

En agosto de 2014, la investigadora brasileña Gabriela Barreto Lemos y su equipo pudieron "tomar fotografías" de objetos que utilizan fotones que no habían interactuado con los sujetos, pero que estaban entrelazados con fotones que sí interactuaban con dichos objetos. Lemos, de la Universidad de Viena, confía en que esta nueva técnica de imagen cuántica podría encontrar aplicación donde la imagen con poca luz es imprescindible, en campos como la imagen biológica o médica.

Desde 2016, varias empresas, como IBM y Microsoft, han creado con éxito computadoras cuánticas que permitieron a los desarrolladores y entusiastas de la tecnología experimentar libremente con conceptos de mecánica cuántica, incluido el entrelazamiento cuántico.

Misterio del tiempo

Ha habido sugerencias para ver el concepto de tiempo como un fenómeno emergente que es un efecto secundario del entrelazamiento cuántico. En otras palabras, el tiempo es un fenómeno de enredo, que coloca todas las lecturas de reloj iguales (de relojes correctamente preparados o de cualquier objeto utilizable como reloj) en la misma historia. Esto fue completamente teorizado por primera vez por Don Page y William Wootters en 1983. La ecuación de Wheeler-DeWitt que combina la relatividad general y la mecánica cuántica, dejando de lado el tiempo por completo, se introdujo en la década de 1960 y se retomó en 1983, cuando Page y Wootters encontraron una solución basada en el entrelazamiento cuántico. Page y Wootters argumentaron que el entrelazamiento se puede usar para medir el tiempo.

Gravedad emergente

Basándose en la correspondencia de AdS/CFT, Mark Van Raamsdonk sugirió que el espacio-tiempo surge como un fenómeno emergente de los grados cuánticos de libertad que están entrelazados y viven en los límites del espacio-tiempo. La gravedad inducida puede surgir de la primera ley de entrelazamiento.

No localidad y entrelazamiento

En los medios de comunicación y la ciencia popular, la no-localidad cuántica es a menudo retratada como equivalente a la enretracción. Si bien esto es cierto para los estados cuánticos bipartitos puros, en general el enredamiento es sólo necesario para las correlaciones no locales, pero existen estados enredados mixtos que no producen tales correlaciones. Un ejemplo conocido es los estados Werner que están enredados para ciertos valores de psSí.m{displaystyle p_{sym}, pero siempre se puede describir utilizando variables ocultas locales. Además, se demostró que, para el número arbitrario de partículas, existen estados que están realmente enredados pero admiten un modelo local. Las pruebas mencionadas sobre la existencia de modelos locales suponen que sólo hay una copia del estado cuántico disponible en un momento. Si las partículas se permiten realizar mediciones locales en muchas copias de tales estados, entonces muchos estados aparentemente locales (por ejemplo, los estados qubit Werner) ya no pueden ser descritos por un modelo local. Esto es, en particular, cierto para todos los estados destilables. Sin embargo, sigue siendo una pregunta abierta si todos los estados enredados se convierten en no locales dados suficientemente muchas copias.

En resumen, el entrelazamiento de un estado compartido por dos partículas es necesario pero no suficiente para que ese estado no sea local. Es importante reconocer que el entrelazamiento se ve más comúnmente como un concepto algebraico, conocido por ser un requisito previo para la no localidad, así como para la teletransportación cuántica y la codificación superdensa, mientras que la no localidad se define de acuerdo con estadísticas experimentales y es mucho más involucrado con los fundamentos e interpretaciones de la mecánica cuántica.

Marco mecánico cuántico

Las siguientes subsecciones son para aquellos con un buen conocimiento práctico de la descripción matemática formal de la mecánica cuántica, incluida la familiaridad con el formalismo y el marco teórico desarrollado en los artículos: notación bra-ket y formulación matemática de la mecánica cuántica.

Estados puros

Considere dos sistemas cuánticos arbitrarios A y B, con sus respectivos espacios de Hilbert H_A y H_B. El espacio de Hilbert del sistema compuesto es el producto tensorial

HA⊗ ⊗ HB.{displaystyle H_{A}otimes H_{B}.

Si el primer sistema está en estado Silencio↑ ↑ .. A{displaystyle Нpsi rangle _{A} y el segundo en estado Silencioφ φ .. B{displaystyle Нphi rangle _{B}, el estado del sistema compuesto es

Silencio↑ ↑ .. A⊗ ⊗ Silencioφ φ .. B.{displaystyle TENpsi rangle _{A}otimes TENphi rangle _{B}

Los estados del sistema compuesto que se pueden representar de esta forma se denominan estados separables o estados producto.

No todos los estados son estados separables (y así los estados del producto). Fijar una base {}Silencioi.. A}{displaystyle ################################################################################################################################################################################################################################################################ ¿Qué? para H_A y una base {}Silencioj.. B}{displaystyle {fnJrangle _{B}}} para H_B. El estado más general en H_A ⊗ H_B es de la forma

Silencio↑ ↑ .. AB=.. i,jcijSilencioi.. A⊗ ⊗ Silencioj.. B{displaystyle TENpsi rangle _{AB}=sum _{i,j}c_{ij} ################################################################################################################################################################################################################################################################.

Este estado es separable si existen vectores [ciA],[cjB]{displaystyle [c_{i}{A}],[c_{j} {B}} así cij=ciAcjB,{displaystyle ¿Qué? rendimiento Silencio↑ ↑ .. A=.. iciASilencioi.. A{textstyle Новpspspncipos _{A}=sum ¿Qué? ¿Qué? y Silencioφ φ .. B=.. jcjBSilencioj.. B.{textstyle ← _{B}=sum _{j}c_{j}{B} _{B} Es inseparable si para cualquier vector [ciA],[cjB]{displaystyle [c_{i}{A}],[c_{j} {B}} al menos por un par de coordenadas ciA,cjB{displaystyle ¿Qué? tenemos cijل ل ciAcjB.{displaystyle C_{ij}neq ¿Qué? Si un estado es inseparable, se llama "estado unido".

Por ejemplo, dadas dos vectores de base {}Silencio0.. A,Silencio1.. A}{displaystyle ################################################################################################################################################################################################################################################################ ¿Qué? de H_A y dos vectores de base {}Silencio0.. B,Silencio1.. B}{displaystyle ################################################################################################################################################################################################################################################################ ¿Qué? de H_B, lo siguiente es un estado enredado:

12()Silencio0.. A⊗ ⊗ Silencio1.. B− − Silencio1.. A⊗ ⊗ Silencio0.. B).{displaystyle {tfrac {1}{sqrt {2}}left(Sobrevivir0rangle _{A}otimes latitud1rangle _{B}-Sobrevivir1rangle ¿Por qué? }

Si el sistema compuesto está en este estado, es imposible atribuirlo al sistema A o al sistema B un estado puro definido. Otra forma de decir esto es que mientras la entropía de von Neumann del estado completo es cero (como lo es para cualquier estado puro), la entropía de los subsistemas es mayor que cero. En este sentido, los sistemas están "enredados". Esto tiene ramificaciones empíricas específicas para la interferometría. El ejemplo anterior es uno de los cuatro estados de Bell, que son (máximamente) estados puros entrelazados (estados puros de H_A ⊗ H_B espacio, pero que no se puede separar en estados puros de cada H _A y H_B).

Ahora supongamos que Alice es observadora del sistema A, y Bob es un observador de sistema B. Si en el estado enredado dado arriba Alice hace una medida en el {}Silencio0.. ,Silencio1.. }{displaystyle ################################################################################################################################################################################################################################################################ {}} eigenbasis of A, hay dos posibles resultados, que se producen con igual probabilidad:

1. Alice mide 0, y el estado del sistema colapsa a Silencio0.. ASilencio1.. B{displaystyle ← _{A} ¿Qué?.
2. Alice mide 1, y el estado del sistema colapsa a Silencio1.. ASilencio0.. B{displaystyle ← _{A} ¿Qué?.

Si ocurre lo primero, entonces cualquier medición subsiguiente realizada por Bob, en la misma base, siempre devolverá 1. Si ocurre lo último (Alice mide 1), entonces la medición de Bob devolverá 0 con certeza. Por lo tanto, el sistema B ha sido alterado por Alice realizando una medición local en el sistema A. Esto sigue siendo cierto incluso si los sistemas A y B están separados espacialmente. Esta es la base de la paradoja EPR.

El resultado de la medición de Alice es aleatorio. Alice no puede decidir en qué estado colapsar el sistema compuesto y, por lo tanto, no puede transmitir información a Bob actuando sobre su sistema. La causalidad se conserva así, en este esquema particular. Para el argumento general, consulte el teorema de no comunicación.

Conjuntos

Como se mencionó anteriormente, el estado de un sistema cuántico viene dado por un vector unitario en un espacio de Hilbert. Más generalmente, si uno tiene menos información sobre el sistema, entonces lo llama un 'conjunto'. y la describe mediante una matriz de densidad, que es una matriz semidefinida positiva, o una clase de traza cuando el espacio de estado es de dimensión infinita y tiene traza 1. Nuevamente, por el teorema espectral, dicha matriz toma la forma general:

*** *** =.. iwiSilencioα α i.. .. α α iSilencio,{displaystyle rho =sum - Hola. # {i}rangle langle alpha _{i}

Donde w_i son probabilidades de valor positivo (suman hasta 1), los vectores α_i son vectores unitarios, y en el caso infinito, tomaríamos el cierre de tales estados en la norma traza. Podemos interpretar *** como representación de un conjunto donde w_i es la proporción del conjunto cuyos estados son Silencioα α i.. {displaystyle Silencioalpha _{i}rangle }. Cuando un estado mixto tiene el rango 1, por lo tanto describe un 'pure ensemble'. Cuando hay menos que información total sobre el estado de un sistema cuántico necesitamos matrices de densidad para representar el estado.

Experimentalmente, un conjunto mixto podría ser realizado como sigue. Considere un aparato "caja negra" que escupe electrones hacia un observador. Los espacios de Hilbert de los electrones son idénticos. El aparato podría producir electrones que están todos en el mismo estado; en este caso, los electrones recibidos por el observador son entonces un conjunto puro. Sin embargo, el aparato podría producir electrones en diferentes estados. Por ejemplo, podría producir dos poblaciones de electrones: una con estado Silencioz+.. {fnMicrosoft Sans Serif} +rangle } con giros alineados en el positivo z dirección, y el otro con estado SilencioSí.− − .. {fnMicrosoft Sans Serif} - ¿Qué? con giros alineados en el negativo Sí. dirección. Generalmente, este es un conjunto mixto, ya que puede haber cualquier número de poblaciones, cada una correspondiente a un estado diferente.

Siguiendo la definición anterior, para un sistema compuesto bipartito, los estados mixtos son simplemente matrices de densidad en H_A ⊗ H _B. Es decir, tiene la forma general

*** *** =.. iwi[.. jc̄ ̄ ij()Silencioα α ij.. ⊗ ⊗ Silencioβ β ij.. )][.. kcik().. α α ikSilencio⊗ ⊗ .. β β ikSilencio)]{displaystyle rho =sum _{i}w_{i}left[sum _{j}{j}bar {c}_{ij}(Sobreviviralpha _{ij}rangle otimes ⋅beta _{ij}rangle)right]left[sum _{k}c_{ik}(langle alpha _{ik} soportaotimes langle beta _{ik} WordPress)right]}

Donde w_i son probabilidades de valor positivo, .. jSilenciocijSilencio2=1{textstyle sum _{j} torturac_{ij}, y los vectores son vectores de unidad. Esto es autoadjunto y positivo y tiene traza 1.

Extendiendo la definición de separabilidad del caso puro, decimos que un estado mixto es separable si se puede escribir como

*** *** =.. iwi*** *** iA⊗ ⊗ *** *** iB,{displaystyle rho =sum ¿Qué? ¿Qué?

Donde w_i son probabilidades de valor positivo y *** *** iA{displaystyle rho _{i}{A}}'s y *** *** iB{displaystyle rho _{i} {B}}'s son en sí mismos estados mixtos (operadores de densidad) en los subsistemas A y B respectivamente. En otras palabras, un estado es separable si es una distribución de probabilidad sobre estados no relacionados o estados de producto. Al escribir las matrices de densidad como sumas de conjuntos puros y en expansión, podemos asumir sin pérdida de generalidad que *** *** iA{displaystyle rho _{i}{A}} y *** *** iB{displaystyle rho _{i} {B}} son ellos mismos conjuntos puros. Entonces se dice que un estado está enredado si no es separable.

En general, se considera difícil averiguar si un estado mixto está entrelazado o no. Se ha demostrado que el caso bipartito general es NP-duro. Para los casos 2 × 2 y 2 × 3, un criterio necesario y suficiente para la separabilidad viene dado por la famosa transposición parcial positiva (PPT) condición.

Matrices de densidad reducida

La idea de una matriz de densidad reducida fue presentada por Paul Dirac en 1930. Considere los sistemas anteriores A y B cada uno con un espacio de Hilbert H_A , H_B. Sea el estado del sistema compuesto

SilencioΨ Ψ .. ▪ ▪ HA⊗ ⊗ HB.{displaystyle 'Psi rangle in H_{A}otimes H_{B}.

Como se indicó anteriormente, en general no hay forma de asociar un estado puro al sistema de componentes A. Sin embargo, todavía es posible asociar una matriz de densidad. Dejar

*** *** T=SilencioΨ Ψ .. .. Ψ Ψ Silencio{displaystyle rho _{T}= durablePsi rangle ;langle Psi tención}.

que es el operador de proyección sobre este estado. El estado de A es la traza parcial de ρ_T sobre la base del sistema B:

*** *** A=def.. jNB()IA⊗ ⊗ .. jSilencioB)()SilencioΨ Ψ .. .. Ψ Ψ Silencio)()IA⊗ ⊗ Silencioj.. B)=TrB*** *** T.{displaystyle rho _{fn} {mhm {fnhm} } {=} sum _{j} {N_{B}left(I_{A}otimes langle j WordPress_{B}derecha)left(sobrevivirPsi rangle langle Psi Silencioderecha)left(I_{A}otimes ⋅jrangle _{B}right)={hbox{Tr}_{B};rho _{T}

La suma se produce sobre NB:=dim⁡ ⁡ ()HB){displaystyle N_{B}:=dim(H_{B} y IA{displaystyle I_{A} el operador de identidad en HA{displaystyle H_{A}. ***_A a veces se llama la matriz de densidad reducida *** on subsystem A. Coloquialmente, "tracemos fuera" sistema B para obtener la matriz de densidad reducida A.

Por ejemplo, la matriz de densidad reducida de A para el estado entrelazado

12()Silencio0.. A⊗ ⊗ Silencio1.. B− − Silencio1.. A⊗ ⊗ Silencio0.. B),{displaystyle {tfrac {1}{sqrt {2}}left(Sobrevivir0rangle _{A}otimes latitud1rangle _{B}-Sobrevivir1rangle ¿Por qué?

discutido anteriormente es

*** *** A=12()Silencio0.. A.. 0SilencioA+Silencio1.. A.. 1SilencioA){displaystyle rho ¿Por qué? ################################################################################################################################################################################################################################################################ ¿Qué? 1 "Primero"

Esto demuestra que, como se esperaba, la matriz de densidad reducida para un conjunto puro enredado es un conjunto mixto. Tampoco sorprendentemente, la matriz de densidad A para el estado del producto puro Silencio↑ ↑ .. A⊗ ⊗ Silencioφ φ .. B{displaystyle Нpsi rangle _{A}otimes Нphi rangle _{B} discutido anteriormente

*** *** A=Silencio↑ ↑ .. A.. ↑ ↑ SilencioA{displaystyle rho _{A}= Toddpsi rangle ################################################################################################################################################################################################################################################################ Silencio..

En general, un estado puro bipartito ρ está entrelazado si y solo si sus estados reducidos son mixtos en lugar de puros.

Dos aplicaciones que las usan

Las matrices de densidad reducida se calcularon explícitamente en diferentes cadenas de espín con un estado fundamental único. Un ejemplo es la cadena de espín AKLT unidimensional: el estado fundamental se puede dividir en un bloque y un entorno. La matriz de densidad reducida del bloque es proporcional a un proyector a un estado fundamental degenerado de otro hamiltoniano.

La matriz de densidad reducida también se evaluó para cadenas de espín XY, donde tiene rango completo. Se demostró que en el límite termodinámico, el espectro de la matriz de densidad reducida de un gran bloque de espines es una secuencia geométrica exacta en este caso.

El enredo como recurso

En la teoría de la información cuántica, los estados entrelazados se consideran un 'recurso', es decir, algo costoso de producir y que permite implementar transformaciones valiosas. El entorno en el que esta perspectiva es más evidente es el de los "laboratorios distantes", es decir, dos sistemas cuánticos etiquetados como "A" y "B" en cada uno de los cuales se pueden realizar operaciones cuánticas arbitrarias, pero que no interactúan entre sí mecánicamente cuánticamente. La única interacción permitida es el intercambio de información clásica, que combinada con las operaciones cuánticas locales más generales da lugar a la clase de operaciones denominadas LOCC (operaciones locales y comunicación clásica). Estas operaciones no permiten la producción de estados entrelazados entre los sistemas A y B. Pero si A y B cuentan con un suministro de estados entrelazados, estos, junto con las operaciones LOCC, pueden permitir una clase más grande de transformaciones. Por ejemplo, se puede realizar una interacción entre un qubit de A y un qubit de B teletransportando primero el qubit de A a B y luego permitiéndole interactuar con el qubit de B (que ahora es una operación LOCC, ya que ambos qubits están en el laboratorio de B) y luego teletransportar el qubit de regreso a A. En este proceso se utilizan dos estados de enredo máximo de dos qubits. Por lo tanto, los estados entrelazados son un recurso que permite la realización de interacciones cuánticas (o de canales cuánticos) en un entorno donde solo están disponibles los LOCC, pero se consumen en el proceso. Hay otras aplicaciones en las que el entrelazamiento puede verse como un recurso, por ejemplo, la comunicación privada o la distinción de estados cuánticos.

Clasificación del enredo

No todos los estados cuánticos son igualmente valiosos como recurso. Para cuantificar este valor, se pueden usar diferentes medidas de entrelazamiento (ver más abajo), que asignan un valor numérico a cada estado cuántico. Sin embargo, a menudo es interesante conformarse con una forma más tosca de comparar estados cuánticos. Esto da lugar a diferentes esquemas de clasificación. La mayoría de las clases de entrelazamiento se definen en función de si los estados se pueden convertir a otros estados utilizando LOCC o una subclase de estas operaciones. Cuanto menor sea el conjunto de operaciones permitidas, mejor será la clasificación. Ejemplos importantes son:

• Si dos estados pueden ser transformados entre sí por una operación unitaria local, se dice que están en el mismo Clase LU. Esta es la mejor de las clases generalmente consideradas. Dos estados de la misma clase LU tienen el mismo valor para las medidas de enredo y el mismo valor que un recurso en el entorno de los lados distantes. Hay un número infinito de diferentes clases de LU (incluso en el caso más simple de dos codos en un estado puro).
• Si dos estados pueden ser transformados entre sí por operaciones locales incluyendo mediciones con probabilidad mayor de 0, se dice que están en la misma 'clase SLOCC' ("LoCC tocástico"). Cualitativamente, dos estados *** *** 1{displaystyle rho ¿Qué? y *** *** 2{displaystyle rho _{2} en la misma clase SLOCC son igualmente poderosos (ya que puedo transformar uno en el otro y luego hacer lo que me permita hacer), pero desde las transformaciones *** *** 1→ → *** *** 2{displaystyle rho _{1}to rho _{2} y *** *** 2→ → *** *** 1{displaystyle rho _{2}to rho ¿Qué? puede tener éxito con diferentes probabilidades, ya no son igualmente valiosos. Por ejemplo, para dos codos puros hay sólo dos clases de SLOCC: los estados enredados (que contiene tanto el (enredado casi) Bell estados y estados débilmente enredados como Silencio00.. +0,01Silencio11.. {displaystyle tención00rangle +0.01 vidas11rangle }) y los separadores (es decir, estados de producto como Silencio00.. {displaystyle Silencioso).
• En lugar de considerar transformaciones de copias individuales de un estado (como *** *** 1→ → *** *** 2{displaystyle rho _{1}to rho _{2}) se puede definir clases basadas en la posibilidad de transformaciones multicopia. Por ejemplo, hay ejemplos cuando *** *** 1→ → *** *** 2{displaystyle rho _{1}to rho _{2} es imposible por LOCC, pero *** *** 1⊗ ⊗ *** *** 1→ → *** *** 2{displaystyle rho _{1}otimes rho _{1}to rho _{2}} es posible. Una clasificación muy importante (y muy gruesa) se basa en la propiedad si es posible transformar un número arbitrario de copias de un estado *** *** {displaystyle rho } al menos un estado puro enredado. Los Estados que tienen esta propiedad se llaman destilables. Estos estados son los estados cuánticos más útiles ya que, dados lo suficiente, pueden ser transformados (con operaciones locales) en cualquier estado enredado y por lo tanto permiten todos los usos posibles. Vino inicialmente como una sorpresa que no todos los estados enredados son destilables, aquellos que no se llaman 'enredados enredados'.

Una clasificación de entrelazamiento diferente se basa en lo que las correlaciones cuánticas presentes en un estado permiten hacer a A y B: se distinguen tres subconjuntos de estados entrelazados: (1) los estados no locales, que producen correlaciones que no pueden explicarse mediante un modelo de variable oculta local y, por lo tanto, violan una desigualdad de Bell, (2) los estados dirigibles que contienen suficientes correlaciones para que A las modifique ("dirigir") mediante mediciones locales, el estado reducido condicional de B de tal manera que A puede demostrarle a B que el estado que posee está enredado, y finalmente (3) esos estados enredados que no son ni no locales ni dirigibles. Los tres conjuntos no están vacíos.

Entropía

En esta sección, se analiza la entropía de un estado mixto y cómo puede verse como una medida del entrelazamiento cuántico.

Definición

La parcela de von Neumann entropy Vs Eigenvalue para un estado puro bipartito de 2 niveles. Cuando el eigenvalue tiene valor.5, la entropía de von Neumann se encuentra en un máximo, correspondiente al máximo enredamiento.

En la teoría de la información clásica H, la entropía Shannon, está asociada a una distribución de probabilidad, p1,⋯ ⋯ ,pn{displaystyle p_{1},cdotsp_{n}, de la siguiente manera:

H()p1,⋯ ⋯ ,pn)=− − .. ipilog2⁡ ⁡ pi.{displaystyle H(p_{1},cdotsp_{n}=-sum ¿Por qué? _{2}p_{i}

Dado que un estado mixto ρ es una distribución de probabilidad sobre un conjunto, esto lleva naturalmente a la definición de la entropía de von Neumann:

S()*** *** )=− − Tr()*** *** log2⁡ ⁡ *** *** ).{displaystyle S(rho)=-{hbox{Tr}left(rho log _{2}{rho }right). }

En general, se utiliza el cálculo funcional Borel para calcular una función no polinomio como log₂()***). Si el operador no negativo *** actúa en un espacio Hilbert de dimensiones finitas y tiene eigenvalues λ λ 1,⋯ ⋯ ,λ λ n{displaystyle lambda _{1},cdotslambda ¿Qué?, log₂()***) resulta ser nada más que el operador con los mismos eigenvectores, pero los eigenvalues log2⁡ ⁡ ()λ λ 1),⋯ ⋯ ,log2⁡ ⁡ ()λ λ n){displaystyle log _{2}(lambda _{1}),cdotslog _{2}(lambda _{n})}. La entropía de Shannon es entonces:

S()*** *** )=− − Tr()*** *** log2⁡ ⁡ *** *** )=− − .. iλ λ ilog2⁡ ⁡ λ λ i{displaystyle S(rho)=-{hbox{Tr}left(rho log _{2}{rho }right)=-sum _{i}lambda ¿Qué? "Lambda" ¿Qué?.

Dado que un evento de probabilidad 0 no debería contribuir a la entropía, y dado que

limp→ → 0plog⁡ ⁡ p=0,{displaystyle lim _{pto 0}plog p=0,}

se adopta la convención 0 log(0) = 0. Esto también se extiende al caso de dimensión infinita: si ρ tiene resolución espectral

*** *** =∫ ∫ λ λ dPλ λ ,{displaystyle rho =int lambda DP_{lambda },}

asumir la misma convención al calcular

*** *** log2⁡ ⁡ *** *** =∫ ∫ λ λ log2⁡ ⁡ λ λ dPλ λ .{displaystyle rho log _{2}rho =int lambda log _{2}lambda dP_{lambda }

Al igual que en la mecánica estadística, cuanto mayor sea la incertidumbre (número de microestados) que debe poseer el sistema, mayor será la entropía. Por ejemplo, la entropía de cualquier estado puro es cero, lo que no sorprende ya que no hay incertidumbre sobre un sistema en estado puro. La entropía de cualquiera de los dos subsistemas del estado entrelazado discutidos anteriormente es log(2) (que se puede demostrar que es la entropía máxima para 2×2estados mixtos).

Como medida de enredo

La entropía proporciona una herramienta que se puede utilizar para cuantificar el entrelazamiento, aunque existen otras medidas de entrelazamiento. Si el sistema general es puro, la entropía de un subsistema se puede usar para medir su grado de entrelazamiento con los otros subsistemas. Para estados puros bipartitos, la entropía de von Neumann de estados reducidos es la única medida de entrelazamiento en el sentido de que es la única función en la familia de estados que satisface ciertos axiomas requeridos de una medida de entrelazamiento.

Es un resultado clásico que la entropía de Shannon alcanza su máximo en, y solo en, la distribución de probabilidad uniforme {1/n,...,1/n}. Por lo tanto, un estado puro bipartito ρ ∈ H_A ⊗ H_B se dice que es un estado máximamente entrelazado si el estado reducido de cada subsistema de ρ es la matriz diagonal

[1n⋱ ⋱ 1n].{displaystyle {begin{bmatrix}{n} {fn} limitándose\\\ddots <\\\\fnMicroc {1}end{bmatrix}}}

Para estados mixtos, la entropía reducida de von Neumann no es la única medida de entrelazamiento razonable.

Aparte, la definición de la teoría de la información está estrechamente relacionada con la entropía en el sentido de la mecánica estadística (comparando las dos definiciones en el presente contexto, se acostumbra establecer la constante de Boltzmann k = 1). Por ejemplo, por propiedades del cálculo funcional de Borel, vemos que para cualquier operador unitario U,

S()*** *** )=S()U*** *** UAlternativa Alternativa ).{displaystyle S(rho)=Sleft(Urho U^{*}right). }

De hecho, sin esta propiedad, la entropía de von Neumann no estaría bien definida.

En particular, U podría ser el operador de evolución temporal del sistema, es decir,

U()t)=exp⁡ ⁡ ()− − iHt▪ ▪ ),{displaystyle U(t)=exp left({frac {-iHt} {hbar}}derecho),}

donde H es el hamiltoniano del sistema. Aquí la entropía no cambia.

La reversibilidad de un proceso está asociada con el cambio de entropía resultante, es decir, un proceso es reversible si, y solo si, deja invariable la entropía del sistema. Por lo tanto, la marcha de la flecha del tiempo hacia el equilibrio termodinámico es simplemente la creciente expansión del entrelazamiento cuántico. Esto proporciona una conexión entre la teoría de la información cuántica y la termodinámica.

La entropía de Rényi también se puede usar como una medida de entrelazamiento.

Medidas de enredo

Las medidas de entrelazamiento cuantifican la cantidad de entrelazamiento en un estado cuántico (a menudo visto como bipartito). Como se mencionó anteriormente, la entropía de entrelazamiento es la medida estándar de entrelazamiento para estados puros (pero ya no es una medida de entrelazamiento para estados mixtos). Para estados mixtos, existen algunas medidas de enredo en la literatura y ninguna es estándar.

• Costo de participación
• Enredamiento destilable
• Enredamiento de la formación
• Concurrencia
• Entropía relativa de enredamiento
• Enredamiento escalonado
• negatividad logarítmica

La mayoría (pero no todas) de estas medidas de entrelazamiento se reducen para los estados puros a la entropía de entrelazamiento y son difíciles (NP-difíciles) de calcular.

Teoría cuántica de campos

El teorema de Reeh-Schlieder de la teoría cuántica de campos a veces se considera un análogo del entrelazamiento cuántico.

Aplicaciones

El entrelazamiento tiene muchas aplicaciones en la teoría de la información cuántica. Con la ayuda del enredo, se pueden lograr tareas que de otro modo serían imposibles.

Entre las aplicaciones más conocidas del entrelazamiento se encuentran la codificación superdensa y la teletransportación cuántica.

La mayoría de los investigadores creen que el entrelazamiento es necesario para realizar la computación cuántica (aunque algunos lo cuestionan).

El entrelazamiento se usa en algunos protocolos de criptografía cuántica, pero para probar la seguridad de QKD bajo supuestos estándar no se requiere entrelazamiento. Sin embargo, la seguridad independiente del dispositivo de QKD se muestra explotando el enredo entre los socios de comunicación.

Estados entrelazados

Hay varios estados entrelazados canónicos que aparecen a menudo en la teoría y los experimentos.

Para dos qubits, los estados de Bell son

SilencioCCPR CCPR ± ± .. =12()Silencio0.. A⊗ ⊗ Silencio0.. B± ± Silencio1.. A⊗ ⊗ Silencio1.. B){displaystyle Silencio. ################################################################################################################################################################################################################################################################

SilencioΨ Ψ ± ± .. =12()Silencio0.. A⊗ ⊗ Silencio1.. B± ± Silencio1.. A⊗ ⊗ Silencio0.. B).{displaystyle Silencioso. _{A}otimes tención1rangle _{B}pm TEN1rangle _{A}otimes TEN0rangle _{B}).

Estos cuatro estados puros están entrelazados al máximo (según la entropía del entrelazamiento) y forman una base ortonormal (álgebra lineal) del espacio de Hilbert de los dos qubits. Juegan un papel fundamental en el teorema de Bell.

Para M>2 qubits, el estado GHZ es

SilencioGHZ.. =Silencio0.. ⊗ ⊗ M+Silencio1.. ⊗ ⊗ M2,{displaystyle Нmathrm {GHZ} rangle ={frac {Sobrevivir0rangle ^{otimes M}+ sobrevivir1rangle ^{otimes M}{sqrt {2}}}}}}}

que reduce al estado de Bell SilencioCCPR CCPR +.. {displaystyle Silencio. para M=2{displaystyle M=2}. El estado tradicional de GHZ fue definido para M=3{displaystyle M=3}. Los estados de GHZ se extienden ocasionalmente a los cuartos, es decir, los sistemas de d en lugar de 2 dimensiones.

También para M>2 qubits, existen estados de espín apretado, una clase de estados coherentes apretados que satisfacen ciertas restricciones sobre la incertidumbre de las mediciones de espín, que necesariamente están entrelazados. Los estados de espín comprimido son buenos candidatos para mejorar las mediciones de precisión mediante el entrelazamiento cuántico.

Para dos modos bosónicos, un estado MEDIODÍA es

Silencio↑ ↑ NO.. =SilencioN.. aSilencio0.. b+Silencio0.. aSilencioN.. b2,{displaystyle ← _{text{NOON}rangle ={frac ################################################################################################################################################################################################################################################################ ¿Por qué? _{a}Sobrevivir ¿Qué? {2}}},,}

Esto es como el estado de Bell SilencioΨ Ψ +.. {displaystyle Silencio. excepto los kets base 0 y 1 han sido reemplazados por "el N los fotones están en un modo y "los N los fotones están en el otro modo".

Por último, también existen estados de Fock gemelos para los modos bosónicos, que se pueden crear alimentando un estado de Fock en dos brazos que conducen a un divisor de haz. Son la suma de múltiplos de los estados del MEDIODÍA y se pueden utilizar para alcanzar el límite de Heisenberg.

Para las medidas de entrelazamiento elegidas apropiadamente, los estados de Bell, GHZ y MEDIODÍA se entrelazan al máximo, mientras que los estados de espín apretado y Fock gemelo solo se entrelazan parcialmente. Los estados parcialmente entrelazados son generalmente más fáciles de preparar experimentalmente.

Métodos para crear enredos

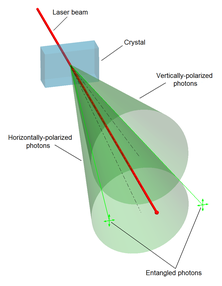
El entrelazamiento generalmente se crea por interacciones directas entre partículas subatómicas. Estas interacciones pueden adoptar numerosas formas. Uno de los métodos más utilizados es la conversión descendente paramétrica espontánea para generar un par de fotones entrelazados en polarización. Otros métodos incluyen el uso de un acoplador de fibra para confinar y mezclar fotones, fotones emitidos por la cascada de decaimiento del bi-excitón en un punto cuántico, el uso del efecto Hong-Ou-Mandel, etc. Entrelazamiento cuántico de una partícula y su Las antipartículas, como un electrón y un positrón, se pueden crear mediante la superposición parcial de las funciones de onda cuánticas correspondientes en el interferómetro de Hardy. En las primeras pruebas del teorema de Bell, las partículas entrelazadas se generaban mediante cascadas atómicas.

También es posible crear entrelazamientos entre sistemas cuánticos que nunca interactuaron directamente, mediante el uso del intercambio de entrelazamientos. Dos partículas idénticas preparadas independientemente también pueden estar entrelazadas si sus funciones de onda simplemente se superponen espacialmente, al menos parcialmente.

Prueba de enredos en un sistema

Una matriz de densidad ρ se llama separable si se puede escribir como una suma convexa de estados del producto, a saber

*** *** =.. jpj*** *** j()A)⊗ ⊗ *** *** j()B){displaystyle {rho =cH003} ¿Por qué?

1≥ ≥ pj≥ ≥ 0{displaystyle 1geq p_{j}geq 0}

Para los sistemas 2-Qubit y Qubit-Qutrit (2 × 2 y 2 × 3 respectivamente), el criterio simple de Peres-Horodecki proporciona un criterio tanto necesario como suficiente para la separabilidad y, por lo tanto, inadvertidamente, para detectar entrelazamientos. Sin embargo, para el caso general, el criterio es simplemente necesario para la separabilidad, ya que el problema se vuelve NP-difícil cuando se generaliza. Otros criterios de separabilidad incluyen (pero no se limitan a) el criterio de rango, el criterio de reducción y aquellos basados en relaciones de incertidumbre. Ver ref. para una revisión de los criterios de separabilidad en sistemas de variables discretas y Ref. para una revisión de técnicas y desafíos en la certificación de entrelazamiento experimental en sistemas de variables discretas.

Jon Magne Leinaas, Jan Myrheim y Eirik Ovrum sugieren un enfoque numérico del problema en su artículo "Aspectos geométricos del enredo". Leonas et al. ofrecen un enfoque numérico, refinando iterativamente un estado separable estimado hacia el estado objetivo que se va a probar y verificando si el estado objetivo se puede alcanzar. Una implementación del algoritmo (que incluye una prueba de criterio de Peres-Horodecki integrada) es "StateSeparator" Aplicación Web.

En sistemas variables continuos, también se aplica el criterio Peres-Horodecki. Específicamente, Simon formuló una versión particular del criterio Peres-Horodecki en términos de los momentos de segundo orden de los operadores canónicos y demostró que es necesario y suficiente para 1⊕ ⊕ 1{displaystyle 1oplus 1}-mode Gaussian states (ver Ref. para un enfoque aparentemente diferente pero esencialmente equivalente). Más tarde se encontró que la condición de Simon también es necesaria y suficiente para 1⊕ ⊕ n{displaystyle 1oplus n}-Mode Gaussian states, but no longer sufficient for 2⊕ ⊕ 2{displaystyle 2oplus 2}-Mode Gaussian states. La condición de Simon puede generalizarse teniendo en cuenta los momentos de orden superior de los operadores canónicos o utilizando medidas entropicas.

En 2016, China lanzó el primer satélite de comunicaciones cuánticas del mundo. La misión Experimentos Cuánticos a Escala Espacial (QUESS) de 100 millones de dólares se lanzó el 16 de agosto de 2016 desde el Centro de Lanzamiento de Satélites de Jiuquan en el norte de China a la 01:40 hora local.

Durante los próximos dos años, la nave, apodada "Micius" después del antiguo filósofo chino, demostrará la viabilidad de la cuántica comunicación entre la Tierra y el espacio, y probar el entrelazamiento cuántico en distancias sin precedentes.

En la edición del 16 de junio de 2017 de Science, Yin et al. informe que establece un nuevo récord de distancia de entrelazamiento cuántico de 1.203 km, lo que demuestra la supervivencia de un par de dos fotones y una violación de una desigualdad de Bell, alcanzando una valoración CHSH de 2,37 ± 0,09, en condiciones estrictas de la localidad de Einstein, desde el satélite Micius hasta las bases en Lijian, Yunnan y Delingha, Quinhai, aumentando en un orden de magnitud la eficiencia de la transmisión con respecto a los experimentos de fibra óptica anteriores.

Sistemas naturalmente entrelazados

Las capas de electrones de los átomos multielectrónicos siempre consisten en electrones entrelazados. La energía de ionización correcta solo se puede calcular considerando el entrelazamiento de electrones.

Fotosíntesis

Se ha sugerido que en el proceso de la fotosíntesis, el entrelazamiento está involucrado en la transferencia de energía entre los complejos captadores de luz y los centros de reacción fotosintéticos donde la energía de cada fotón absorbido se recolecta en forma de energía química. Sin tal proceso, no se puede explicar la conversión eficiente de la luz en energía química. Usando espectroscopía de femtosegundos, la coherencia del entrelazamiento en el complejo Fenna-Matthews-Olson se midió durante cientos de femtosegundos (un tiempo relativamente largo en este sentido), lo que respalda esta teoría. Sin embargo, estudios críticos de seguimiento cuestionan la interpretación de estos resultados y asignan las firmas reportadas de coherencia cuántica electrónica a la dinámica nuclear en los cromóforos oa los experimentos que se realizan a temperaturas criogénicas en lugar de fisiológicas.

Enredo de objetos macroscópicos

En 2020, los investigadores informaron sobre el entrelazamiento cuántico entre el movimiento de un oscilador mecánico de tamaño milimétrico y un sistema de espín distante dispar de una nube de átomos. El trabajo posterior complementó este trabajo entrelazando cuánticamente dos osciladores mecánicos.

Entrelazamiento de elementos de sistemas vivos

En octubre de 2018, los físicos informaron que se producía un entrelazamiento cuántico utilizando organismos vivos, en particular entre moléculas fotosintéticas dentro de bacterias vivas y luz cuantificada.

Se han estudiado organismos vivos (bacterias verdes del azufre) como mediadores para crear un entrelazamiento cuántico entre modos de luz que de otro modo no interactuarían, lo que muestra un alto entrelazamiento entre los modos de luz y bacterias y, hasta cierto punto, incluso entrelazamiento dentro de las bacterias.