Energía libre de gibbs

format_list_bulleted Contenido keyboard_arrow_down

ImprimirCitar

Tipo de potencial termodinámico; útil para calcular el trabajo reversible en ciertos sistemas

En la termodinámica, Gibbs energía libre (o Energía de Gibbs como nombre recomendado; símbolo $G$ ) es un potencial termodinámico que se puede utilizar para calcular la cantidad máxima de trabajo, aparte del trabajo de volumen de presión, que puede ser realizado por un sistema termodinámico cerrado a temperatura y presión constantes. También proporciona una condición necesaria para procesos tales como reacciones químicas que pueden ocurrir en estas condiciones. La energía libre de Gibbs se expresa como

{displaystyle G(p,T)=U+pV-TS=H-TS}

donde p es la presión, T es la temperatura, U es la energía interna, V es el volumen, H es la entalpía y S es la entropía.

El cambio de energía libre de Gibbs () ${displaystyle Delta G=Delta H-TDelta S}$ , medido en joules en SI) es el máximo cantidad de trabajo de expansión no volumen que se puede extraer de un sistema cerrado (uno que puede intercambiar calor y trabajar con su entorno, pero no importa) a temperatura y presión fijas. Este máximo se puede alcanzar sólo en un proceso completamente reversible. Cuando un sistema se transforma reversiblemente de un estado inicial a un estado final bajo estas condiciones, la disminución de la energía libre de Gibbs equivale al trabajo realizado por el sistema a su entorno, menos el trabajo de las fuerzas de presión.

La energía de Gibbs es el potencial termodinámico que se minimiza cuando un sistema alcanza el equilibrio químico a presión y temperatura constantes cuando no es impulsado por un voltaje electrolítico aplicado. Su derivado con respecto a la coordinación de reacción del sistema entonces desaparece en el punto de equilibrio. Como tal, una reducción $G$ es necesario para que una reacción sea espontánea bajo estas condiciones.

El concepto de energía libre de Gibbs, originalmente llamado energía disponible, fue desarrollado en la década de 1870 por el científico estadounidense Josiah Willard Gibbs. En 1873, Gibbs describió esta "energía disponible" como

la mayor cantidad de trabajo mecánico que se puede obtener de una cantidad determinada de una sustancia en un estado inicial dado, sin aumentar su volumen total o permitir que el calor pase a o desde cuerpos externos, excepto como al cierre de los procesos se deja en su condición inicial.

Se supone que el estado inicial del cuerpo, según Gibbs, es tal que "se puede hacer que el cuerpo pase de él a estados de energía disipada mediante procesos reversibles". En su obra magna de 1876 Sobre el equilibrio de las sustancias heterogéneas, un análisis gráfico de los sistemas químicos multifásicos, se comprometió por completo con sus pensamientos sobre la energía libre de químicos.

Si los reaccionarios y productos están todos en sus estados estándar termodinámicos, entonces la ecuación definitoria está escrita como ${displaystyle Delta G^{circ }=Delta H^{circ }-TDelta S^{circ }}$ , donde $H$ es enthalpy, $T$ es temperatura absoluta, y $S$ es entropía.

Resumen

La reacción C_s)^diamante→ C_s)^grafito tiene un cambio negativo en la energía libre de Gibbs y es por lo tanto termodinámicamente favorable a 25 °C y 1 atm. Sin embargo, la reacción es demasiado lenta para ser observada, debido a su muy alta energía de activación. Si una reacción es termodinámicamente favorable no determina su tasa.

De acuerdo con la segunda ley de la termodinámica, para sistemas que reaccionan a temperatura y presión fijas sin entrada de trabajo que no sea volumen de presión (pV), existe una tendencia natural general a lograr un mínimo de Energía libre de Gibbs.

Una medida cuantitativa de la favorabilidad de una reacción dada bajo estas condiciones es el cambio ΔG (a veces escrito "delta G" o & #34;dG") en la energía libre de Gibbs que es (o sería) causada por la reacción. Como condición necesaria para que la reacción ocurra a temperatura y presión constantes, ΔG debe ser menor que el trabajo sin volumen de presión (sin pV, por ejemplo, eléctrico), que a menudo es igual a cero (entonces ΔG debe ser negativo). ΔG es igual a la cantidad máxima de trabajo no pV que se puede realizar como resultado de la reacción química para el caso de un proceso reversible. Si el análisis indica un ΔG positivo para una reacción, entonces se tendría que agregar energía, en forma de trabajo eléctrico u otro no pV, al sistema de reacción para ΔG sea menor que el trabajo no pV y haga posible que ocurra la reacción.

Se puede pensar en ∆G como la cantidad de "gratis" o "útil" energía disponible para realizar trabajo no pV a temperatura y presión constantes. La ecuación también se puede ver desde la perspectiva del sistema tomado junto con su entorno (el resto del universo). Primero, se supone que la reacción dada a temperatura y presión constantes es la única que está ocurriendo. Entonces la entropía liberada o absorbida por el sistema es igual a la entropía que el entorno debe absorber o liberar, respectivamente. La reacción solo se permitirá si el cambio de entropía total del universo es cero o positivo. Esto se refleja en un ΔG negativo, y la reacción se denomina proceso exergónico.

Si se acoplan dos reacciones químicas, entonces se puede hacer que suceda una reacción endergónica (una con ΔG positivo). La entrada de calor en una reacción inherentemente endergónica, como la eliminación de ciclohexanol a ciclohexeno, puede verse como el acoplamiento de una reacción desfavorable (eliminación) a una favorable (quema de carbón u otra provisión de calor) de tal manera que el cambio de entropía total del universo es mayor o igual a cero, lo que hace que el cambio de energía libre de Gibbs total de las reacciones acopladas sea negativo.

En el uso tradicional, el término "gratis" se incluyó en "Energía libre de Gibbs" para significar "disponible en forma de trabajo útil". La caracterización se hace más precisa si añadimos la calificación de que es la energía disponible para trabajo volumétrico sin presión. (Un significado análogo, pero ligeramente diferente, de 'libre' se aplica junto con la energía libre de Helmholtz, para sistemas a temperatura constante). Sin embargo, un número cada vez mayor de libros y artículos de revistas no incluyen el archivo adjunto "gratis", refiriéndose a G como simplemente "Energía de Gibbs". Este es el resultado de una reunión de la IUPAC de 1988 para establecer terminologías unificadas para la comunidad científica internacional, en la que la eliminación del adjetivo "libre" fue recomendado Este estándar, sin embargo, aún no ha sido adoptado universalmente.

El nombre "entalpía libre" también se usó para G en el pasado.

Historia

La cantidad denominada "energía libre" es un reemplazo más avanzado y preciso del término obsoleto afinidad, que los químicos usaban en los primeros años de la química física para describir la fuerza que causaba las reacciones químicas.

En 1873, Josiah Willard Gibbs publicó Un método de representación geométrica de las propiedades termodinámicas de las sustancias por medio de superficies, en el que esbozaba los principios de su nueva ecuación que podía predecir o estimar las tendencias de varios procesos naturales que se producen cuando los cuerpos o sistemas se ponen en contacto. Al estudiar las interacciones de sustancias homogéneas en contacto, es decir, cuerpos compuestos de parte sólida, parte líquida y parte vapor, y mediante el uso de un gráfico tridimensional de volumen-entropía-energía interna, Gibbs pudo determinar tres estados de equilibrio, es decir, "necesariamente estable", "neutral" e "inestable", y si se producirían o no cambios. Además, Gibbs declaró:

Si queremos expresar en una sola ecuación la condición necesaria y suficiente de equilibrio termodinámico para una sustancia cuando está rodeada por un medio de presión constante p y temperatura T, esta ecuación puede ser escrita:
δ()ε − Tpira + ♪) = 0
cuando δ se refiere a la variación producida por cualquier variación en el estado de las partes del cuerpo, y (cuando diferentes partes del cuerpo están en diferentes estados) en la proporción en que el cuerpo está dividido entre los diferentes estados. La condición del equilibrio estable es que el valor de la expresión en la paréntesis será mínimo.

En esta descripción, tal como la usa Gibbs, ε se refiere a la energía interna del cuerpo, η se refiere a la entropía del cuerpo y ν es el volumen del cuerpo...

Después, en 1882, el científico alemán Hermann von Helmholtz caracterizó la afinidad como la mayor cantidad de trabajo que se puede ganar cuando la reacción se lleva a cabo de manera reversible, por ejemplo, trabajo eléctrico en una celda reversible. Por lo tanto, el trabajo máximo se considera como la disminución de la energía libre o disponible del sistema (energía libre de Gibbs G a T = constante, P = constante o energía libre de Helmholtz F en T = constante, V = constante), mientras que el calor cedido suele ser una medida de la disminución de la energía total del sistema (energía interna). Así, G o F es la cantidad de energía "libre" para trabajar en las condiciones dadas.

Hasta este punto, la opinión general había sido que: "todas las reacciones químicas llevan al sistema a un estado de equilibrio en el que las afinidades de las reacciones se desvanecen". Durante los siguientes 60 años, el término afinidad fue reemplazado por el término energía libre. Según el historiador de química Henry Leicester, el influyente libro de texto de 1923 Thermodynamics and the Free Energy of Chemical Substances de Gilbert N. Lewis y Merle Randall condujo al reemplazo del término "afinidad" por el término "energía libre" en gran parte del mundo de habla inglesa.

Definiciones

Willard Gibbs 1873 energía disponible (energía libre) gráfico, que muestra un plano perpendicular al eje v (volumen) y paso a través del punto A, que representa el estado inicial del cuerpo. MN es la sección de la superficie de la energía disipada. Qε y Q. son secciones de los aviones . = 0 y ε = 0, y por lo tanto paralelo a los ejes de ε (energía interna) y . (entropía), respectivamente. AD y AE son la energía y la entropía del cuerpo en su estado inicial, AB y AC su energía disponible (Gibs free energy) and its capacidad para la entropía (la cantidad por la que se puede aumentar la entropía del cuerpo sin cambiar la energía del cuerpo o aumentar su volumen), respectivamente.

La energía libre de Gibbs se define como

{displaystyle G(p,T)=U+pV-TS,}

que es lo mismo que

{displaystyle G(p,T)=H-TS,}

donde:

U es la energía interna (SI unidad: joule),
p es presión (unidad SI: pascal),
V volumen (unidad SI: m³),
T es la temperatura (unidad SI: kelvin),
S es la entropía (unidad SI: joule per kelvin),
H es el enthalpy (unidad SI: joule).

La expresión del cambio infinitesimal reversible en la energía libre de Gibbs en función de sus "variables naturales" p y T, para un sistema abierto, sujeto a la operación de fuerzas externas (por ejemplo, eléctricas o magnéticas) X_i , que hacen que los parámetros externos del sistema a_i cambien en una cantidad da_i, se puede derivar de la siguiente manera de la primera ley para procesos reversibles:

{displaystyle {begin{aligned}T,mathrm {d} S&=mathrm {d} U+p,mathrm {d} V-sum _{i=1}^{k}mu _{i},mathrm {d} N_{i}+sum _{i=1}^{n}X_{i},mathrm {d} a_{i}+cdots \mathrm {d} (TS)-S,mathrm {d} T&=mathrm {d} U+mathrm {d} (pV)-V,mathrm {d} p-sum _{i=1}^{k}mu _{i},mathrm {d} N_{i}+sum _{i=1}^{n}X_{i},mathrm {d} a_{i}+cdots \mathrm {d} (U-TS+pV)&=V,mathrm {d} p-S,mathrm {d} T+sum _{i=1}^{k}mu _{i},mathrm {d} N_{i}-sum _{i=1}^{n}X_{i},mathrm {d} a_{i}+cdots \mathrm {d} G&=V,mathrm {d} p-S,mathrm {d} T+sum _{i=1}^{k}mu _{i},mathrm {d} N_{i}-sum _{i=1}^{n}X_{i},mathrm {d} a_{i}+cdots end{aligned}}}

donde:

μ_i es el potencial químico del i- el componente químico. (Unidad SI: joules per partícula o joules per mole)
N_i es el número de partículas (o el número de lunares) que componen el i- el componente químico.

Esta es una forma de la ecuación fundamental de Gibbs. En la expresión infinitesimal, el término que involucra el potencial químico explica los cambios en la energía libre de Gibbs que resultan de una entrada o salida de partículas. En otras palabras, se cumple para un sistema abierto o para un sistema cerrado que reacciona químicamente donde los N_i están cambiando. Para un sistema cerrado que no reacciona, este término puede eliminarse.

Se puede agregar cualquier cantidad de términos adicionales, según el sistema en particular que se considere. Además del trabajo mecánico, un sistema puede, además, realizar muchos otros tipos de trabajo. Por ejemplo, en la expresión infinitesimal, la energía de trabajo contráctil asociada con un sistema termodinámico que es una fibra contráctil que se acorta en una cantidad −dl bajo una fuerza f resultaría en un término f dl que se añade. Si una cantidad de carga −de es adquirida por un sistema a un potencial eléctrico Ψ, el trabajo eléctrico asociado a esto es −Ψ de, que estaría incluido en la expresión infinitesimal. Se agregan otros términos de trabajo según los requisitos del sistema.

Cada cantidad en las ecuaciones anteriores se puede dividir por la cantidad de sustancia, medida en moles, para formar energía libre molar de Gibbs. La energía libre de Gibbs es una de las funciones termodinámicas más importantes para la caracterización de un sistema. Es un factor para determinar resultados como el voltaje de una celda electroquímica y la constante de equilibrio para una reacción reversible. En los sistemas isobáricos isotérmicos, la energía libre de Gibbs se puede considerar como una energía "dinámica" cantidad, ya que es una medida representativa de los efectos competitivos de las fuerzas impulsoras entálpicas y entrópicas involucradas en un proceso termodinámico.

Relación con otros parámetros pertinentes

La dependencia de la temperatura de la energía de Gibbs para un gas ideal viene dada por la ecuación de Gibbs-Helmholtz, y su dependencia de la presión viene dada por

{displaystyle {frac {G}{N}}={frac {G^{circ }}{N}}+kTln {frac {p}{p^{circ }}}.}

o más convenientemente como su potencial químico:

{displaystyle {frac {G}{N}}=mu =mu ^{circ }+kTln {frac {p}{p^{circ }}}.}

En los sistemas no ideales, entra en juego la fugacidad.

Derivación

El diferencial total de energía libre de Gibbs con respecto a las variables naturales puede obtenerse mediante transformadas de Legendre de la energía interna.

{displaystyle mathrm {d} U=T,mathrm {d} S-p,mathrm {d} V+sum _{i}mu _{i},mathrm {d} N_{i}.}

La definición de G de arriba es

{displaystyle G=U+pV-TS}

Tomando el diferencial total, tenemos

{displaystyle mathrm {d} G=mathrm {d} U+p,mathrm {d} V+V,mathrm {d} p-T,mathrm {d} S-S,mathrm {d} T.}

Reemplazando dU con el resultado de la primera ley da

{displaystyle {begin{aligned}mathrm {d} G&=T,mathrm {d} S-p,mathrm {d} V+sum _{i}mu _{i},mathrm {d} N_{i}+p,mathrm {d} V+V,mathrm {d} p-T,mathrm {d} S-S,mathrm {d} T\&=V,mathrm {d} p-S,mathrm {d} T+sum _{i}mu _{i},mathrm {d} N_{i}.end{aligned}}}

Las variables naturales de G son entonces p, T y {N_i}.

Sistemas homogéneos

Debido a que S, V y N_i son variables extensivas, una relación de Euler permite una fácil integración de dU:

{displaystyle U=TS-pV+sum _{i}mu _{i}N_{i}.}

Debido a que algunas de las variables naturales de G son intensivas, es posible que dG no se integre usando las relaciones de Euler como es el caso de la energía interna. Sin embargo, simplemente sustituyendo el resultado integrado anterior por U en la definición de G da una expresión estándar para G:

{displaystyle {begin{aligned}G&=U+pV-TS\&=left(TS-pV+sum _{i}mu _{i}N_{i}right)+pV-TS\&=sum _{i}mu _{i}N_{i}.end{aligned}}}

Este resultado muestra que el potencial químico de una sustancia $i$ es su (partial) mol(ecul)ar Gibbs energía libre. Se aplica a sistemas homogéneos, macroscópicos, pero no a todos los sistemas termodinámicos.

Energía libre de Gibbs de las reacciones

El sistema que se examina se mantiene a temperatura y presión constantes, y está cerrado (no importa puede entrar o salir). La energía de Gibbs de cualquier sistema es ${displaystyle G=U+pV-TS}$ y un cambio infinitesimal en G, a temperatura y presión constantes, rendimientos

{displaystyle dG=dU+pdV-TdS}

Por la primera ley de la termodinámica, un cambio en la energía interna U viene dado por

dU=delta Q+delta W

donde $δQ$ es energía añadida como calor, y $δW$ es energía añadida como trabajo. El trabajo realizado en el sistema se puede escribir como $δW = - pdV + δW x$ , donde $- pdV$ es el trabajo mecánico de compresión/expansión realizado en o por el sistema y $δW x$ es todas las demás formas de trabajo, que pueden incluir eléctricas, magnéticas, etc. Entonces

{displaystyle dU=delta Q-pdV+delta W_{x}}

y el cambio infinitesimal en G es

{displaystyle dG=delta Q-TdS+delta W_{x}}

La segunda ley de la termodinámica establece que para un sistema cerrado a temperatura constante (en un baño de calor), ${displaystyle TdSgeq delta Q}$ , y así sigue que

{displaystyle dGleq delta W_{x}}

Suponiendo que solo se realiza trabajo mecánico, esto se simplifica a

{displaystyle dGleq 0}

Esto significa que para tal sistema cuando no está en equilibrio, la energía de Gibbs siempre será decreciente, y en equilibrio, el cambio infinitesimal dG será cero. En particular, esto será cierto si el sistema está experimentando una serie de reacciones químicas internas en su camino hacia el equilibrio.

En termodinámica electroquímica

Cuando la carga eléctrica dQ_Ele se pasa entre los electrodos de una célula electroquímica generando un emf ${mathcal {E}}$ , un término de trabajo eléctrico aparece en la expresión para el cambio de la energía de Gibbs:

{displaystyle dG=-SdT+Vdp+{mathcal {E}}dQ_{ele},}

SVpT

La combinación ( ${mathcal {E}}$ , Q_Ele) es un ejemplo de un par conjugado de variables. A presión constante la ecuación anterior produce una relación Maxwell que vincula el cambio en el voltaje de célula abierta con la temperatura T (una cantidad mensurable) al cambio de entropía S cuando la carga se transmite esotérmicamente y isobaricamente. Este último está estrechamente relacionado con la reacción entropía de la reacción electroquímica que otorga a la batería su poder. Esta relación Maxwell es:

{displaystyle left({frac {partial {mathcal {E}}}{partial T}}right)_{Q_{ele},p}=-left({frac {partial S}{partial Q_{ele}}}right)_{T,p}}

Si un mol de iones se disuelve (por ejemplo, en una celda de Daniell, como se explica a continuación), la carga a través del circuito externo es

{displaystyle Delta Q_{ele}=-n_{0}F_{0},,}

Donde n₀ es el número de electrones/ion, y F₀ es la constante de Faraday y el signo menos indica la descarga de la célula. Asumiendo presión y volumen constantes, las propiedades termodinámicas de la célula están relacionadas estrictamente con el comportamiento de su emf por

{displaystyle Delta H=-n_{0}F_{0}left({mathcal {E}}-T{frac {d{mathcal {E}}}{dT}}right),}

donde ΔH es la entalpía de reacción. Las cantidades de la derecha son todas directamente medibles.

Identidades útiles para derivar la ecuación de Nernst

Durante una reacción electroquímica reversible a temperatura y presión constantes, se cumplen las siguientes ecuaciones que involucran la energía libre de Gibbs:

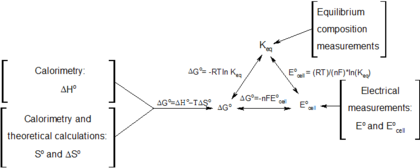
${displaystyle Delta _{text{r}}G=Delta _{text{r}}G^{circ }+RTln Q_{text{r}}}$ (ver equilibrio químico),
${displaystyle Delta _{text{r}}G^{circ }=-RTln K_{text{eq}}}$ (para un sistema en equilibrio químico),
${displaystyle Delta _{text{r}}G=w_{text{elec,rev}}=-nF{mathcal {E}}}$ (para un proceso electroquímico reversible a temperatura y presión constantes),
${displaystyle Delta _{text{r}}G^{circ }=-nF{mathcal {E}}^{circ }}$ (definición de ${displaystyle {mathcal {E}}^{circ }}$ ),

y la reorganización da

{displaystyle {begin{aligned}nF{mathcal {E}}^{circ }&=RTln K_{text{eq}},\nF{mathcal {E}}&=nF{mathcal {E}}^{circ }-RTln Q_{text{r}},\{mathcal {E}}&={mathcal {E}}^{circ }-{frac {RT}{nF}}ln Q_{text{r}},end{aligned}}}

que relaciona el potencial de celda resultante de la reacción con la constante de equilibrio y el cociente de reacción para esa reacción (ecuación de Nernst),

dónde

$Δ r G$ , Gibbs cambio de energía libre por topo de reacción,
$Δ r G°$ , Gibbs cambio de energía libre por topo de reacción para reaccionarios y productos no mezclados en condiciones estándar (es decir, 298K, 100kPa, 1M de cada reaccionante y producto),
$R$ , constante de gas,
$T$ , temperatura absoluta,
$In$ , logaritmo natural,
$Q r$ , cociente de reacción (sin unidad),
$K eq$ , constante de equilibrio (sin unidad),
$w elec,rev$ , trabajo eléctrico en un proceso reversible (convención del signo de química),
$n$ , número de lunares de electrones transferidos en la reacción,
$F = N A e Entendido 96485 C/mol$ , Faraday constante (carga por topo de electrones),
${mathcal {E}}$ , potencial celular,
${displaystyle {mathcal {E}}^{circ }}$ , potencial celular estándar.

Además, también tenemos

{displaystyle {begin{aligned}K_{text{eq}}&=e^{-{frac {Delta _{text{r}}G^{circ }}{RT}}},\Delta _{text{r}}G^{circ }&=-RTleft(ln K_{text{eq}}right)=-2.303,RTleft(log _{10}K_{text{eq}}right),end{aligned}}}

que relaciona la constante de equilibrio con la energía libre de Gibbs. Esto implica que en el equilibrio

{displaystyle Q_{text{r}}=K_{text{eq}}}

{displaystyle Delta _{text{r}}G=0.}

Cambio de formación de energía de Gibbs estándar

Cuadro de sustancias seleccionadas
Sustancia (estado)	Δ_fG°
Sustancia (estado)	(kJ/mol)	(kcal/mol)
NO g)	87.6	20,9
NO₂g)	51.3	12.3
N₂O(g)	103,7	24.78
H₂O(g)	−228.6	−54.64
H₂O(l)	−237.1	−56.67
CO₂g)	−394.4	−94.26
CO(g)	−137.2	−32.79
CH₄g)	−50,5	−12.1
C₂H₆g)	−32.0	−7.65
C₃H₈g)	−23.4	5 a 59
C₆H₆g)	129.7	29.76
C₆H₆l)	124,5	31.00

La energía libre de Gibbs estándar de formación de un compuesto es el cambio de energía libre de Gibbs que acompaña a la formación de 1 mol de esa sustancia a partir de sus elementos componentes, en sus estados estándar (la forma más estable del elemento a 25 ° C y 100 kPa). Su símbolo es Δ_fG˚.

Todos los elementos en sus estados estándar (gas de oxígeno diatómico, grafito, etc.) tienen un cambio de formación de energía libre de Gibbs estándar igual a cero, ya que no hay cambio involucrado.

Δ_fG = Δ_fG̊ + RT In Q_f,

donde Q_f es el cociente de reacción.

En el equilibrio, Δ_fG = 0, y Q_f = K, por lo que la ecuación se convierte en

Δ_fG̊ = −RT In K,

donde K es la constante de equilibrio de la reacción de formación de la sustancia a partir de los elementos en sus estados estándar.

Interpretación gráfica de Gibbs

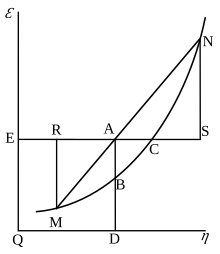
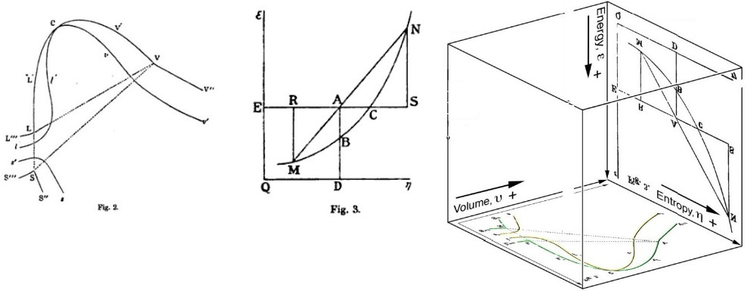
La energía libre de Gibbs se definió originalmente gráficamente. En 1873, el científico estadounidense Willard Gibbs publicó su primer artículo sobre termodinámica, "Métodos gráficos en la termodinámica de fluidos", en el que Gibbs utilizó las dos coordenadas de entropía y volumen para representar el estado del cuerpo. En su segundo artículo de seguimiento, 'A Method of Geometrical Representation of the Thermodynamic Properties of Substances by Means of Surfaces', publicado más tarde ese año, Gibbs agregó en la tercera coordenada de la energía del cuerpo, definida en tres cifras. En 1874, el físico escocés James Clerk Maxwell utilizó Gibbs' figuras para hacer una superficie termodinámica 3D de energía-entropía-volumen de una sustancia ficticia similar al agua. Por lo tanto, para comprender el concepto de energía libre de Gibbs, puede ser útil comprender su interpretación por Gibbs como la sección AB en su figura 3, y como Maxwell esculpió esa sección en su figura de superficie 3D.

El científico estadounidense Willard Gibbs 1873 figura dos y tres (ambos izquierda y media) utilizados por el físico escocés James Clerk Maxwell en 1874 para crear una entropía tridimensional, volumen, energía superficie termodinámica diagrama para una sustancia ficticia similar al agua, transpuesto las dos figuras de Gibbs (a la derecha) en las coordenadas de volumen-entropía (transpuesto a la parte inferior del cubo) y coordenadas de energía-entropía (derribado y transpuesto a la parte posterior del cubo), respectivamente, de una coordenadas cartesianas tridimensionales; la región AB es la primera representación tridimensional de Gibbs siendo energía libre

Notas y referencias

^ a b c Perrot, Pierre (1998). A a Z de la termodinámica. Oxford University Press. ISBN 0-19-856552-6.
^ a b Gibbs, Josiah Willard (diciembre 1873). "Un método de representación geométrica de las propiedades termodinámicas de las sustancias por medios de superficies" (PDF). Transacciones de la Academia de Artes y Ciencias de Connecticut. 2: 382–404.
^ Peter Atkins; Loretta Jones (1 de agosto de 2007). Principios químicos: La búsqueda de la visiónW. H. Freeman. ISBN 978-1-4292-0965-6.
^ Reiss, Howard (1965). Métodos de termodinámica. Dover Publications. ISBN 0-486-69445-3.
^ Calvert, J. G. (1o de enero de 1990). "Glosario de términos de química atmosférica (Recomendaciones 1990)". Química pura y aplicada. 62 (11): 2167–2219. doi:10.1351/pac199062112167.
^ a b "Gibbs energy (function), G". IUPAC Libro de Oro (Compendio de Tecnología Química). IUPAC (Unión Internacional de Química Pura y Aplicada). 2008. doi:10.1351/goldbook.G02629. Retrieved 24 de diciembre 2020. Anteriormente se llamaba energía libre o enthalpy libre.
^ Lehmann, H. P.; Fuentes-Arderiu, X.; Bertello, L. F. (1o de enero de 1996). "Glosario de términos en cantidades y unidades en química clínica (IUPAC-IFCC Recomendaciones 1996)". Química pura y aplicada. 68 (4): 957–1000. doi:10.1351/pac199668040957. S2CID 95196393.
^ Henry Marshall Leicester (1971). El fondo histórico de la química. Courier Corporation. ISBN 978-0-486-61053-5.
^ Potencial químico, IUPAC Gold Book.
^ Müller, Ingo (2007). Una historia de la termodinámica – la doctrina de la energía y la entropía. Springer. ISBN 978-3-540-46226-2.
^ Katchalsky, A.; Curran, Peter F. (1965). Termodinámica en Biofísica. Harvard University Press. CCN 65-22045.
^ Atkins, Peter; de Paula, Julio (2006). Química Física de Atkins (8th ed.). W. H. Freeman. p. 109. ISBN 0-7167-8759-8.
^ a b c Salzman, William R. (2001-08-21). "Open Systems". Termodinámica Química. Universidad de Arizona. Archivado desde el original el 2007-07-07. Retrieved 2007-10-11.
^ Brachman, M. K. (1954). "El nivel de fermi, el potencial químico y la energía libre de Gibbs". The Journal of Chemical Physics. 22 (6): 1152. Bibcode:1954JChPh..22.1152B doi:10.1063/1.1740312.
^ H. S. Harned, B. B. Owen, The Physical Chemistry of Electrolytic Solutions, tercera edición, Reinhold Publishing Corporation, N.Y.,1958, p. 2-6
^ CRC Handbook of Chemistry and Physics, 2009, pp. 5-4-5-42, 90th ed., Lide.
^ James Clerk Maxwell, Elizabeth Garber, Stephen G. Brush, y C. W. Francis Everitt (1995), Maxwell en el calor y la mecánica estadística: en "evitar todas las investigaciones personales" de moléculas, Lehigh University Press, ISBN 0-934223-34-3, p. 248.

Contenido relacionado

Más resultados...