Energía de activación

Las chispas creadas por el acero llamativo contra un pedazo de peinado proporcionan la energía de activación para iniciar la combustión en este quemador Bunsen. La llama azul se sostiene después de que las chispas se detengan porque la continua combustión de la llama es ahora energéticamente favorable.

En química y física, la energía de activación es la cantidad mínima de energía que se debe proporcionar a los compuestos para que produzcan una reacción química. La energía de activación (E_a) de una reacción se mide en julios por mol (J/mol), kilojulios por mol (kJ/mol) o kilocalorías por mol (kcal /mol). La energía de activación se puede considerar como la magnitud de la barrera de potencial (a veces llamada barrera de energía) que separa los mínimos de la superficie de energía potencial correspondiente al estado termodinámico inicial y final. Para que una reacción química avance a una velocidad razonable, la temperatura del sistema debe ser lo suficientemente alta como para que exista un número apreciable de moléculas con energía de traslación igual o mayor que la energía de activación. El término "energía de activación" Fue introducido en 1889 por el científico sueco Svante Arrhenius.

Otros usos

Aunque se usa con menos frecuencia, la energía de activación también se aplica a reacciones nucleares y otros fenómenos físicos.

Dependencia de la temperatura y relación con la ecuación de Arrhenius

La ecuación de Arrhenius proporciona la base cuantitativa de la relación entre la energía de activación y la velocidad a la que se produce una reacción. De la ecuación, la energía de activación se puede encontrar a través de la relación

k=Ae− − Ea/()RT){displaystyle k=Ae^{-E_{textrm {a}}/{(RT)}}}

donde A es el factor preexponencial de la reacción, R es la constante universal de los gases, T es la temperatura absoluta (normalmente en kelvins), y k es el coeficiente de velocidad de reacción. Incluso sin conocer A, E_a puede evaluarse a partir de la variación de los coeficientes de velocidad de reacción en función de la temperatura (dentro de la validez de Arrhenius ecuación).

En un nivel más avanzado, el término de energía de activación neta de Arrhenius de la ecuación de Arrhenius se considera mejor como un parámetro determinado experimentalmente que indica la sensibilidad de la velocidad de reacción a la temperatura. Hay dos objeciones a la asociación de esta energía de activación con la barrera umbral para una reacción elemental. Primero, a menudo no está claro si la reacción procede o no en un solo paso; las barreras de umbral que se promedian sobre todos los pasos elementales tienen poco valor teórico. En segundo lugar, incluso si la reacción que se estudia es elemental, un espectro de colisiones individuales contribuye a las constantes de velocidad obtenidas de experimentos a granel (bulbo) que involucran miles de millones de moléculas, con muchas geometrías y ángulos de colisión de reactivos diferentes, diferentes y (posiblemente) energías vibratorias, todo lo cual puede conducir a diferentes velocidades de reacción microscópicas.

Catalizadores

Ejemplo de una reacción exotérmica enzimática

La relación entre la energía de activación (Ea{displaystyle E_{textrm {}}) y enthalpy de la reacción (Δ)H) con y sin un catalizador, trazado contra la coordinación de reacción. La posición energética más alta (Posición pico) representa el estado de transición. Con el catalizador, la energía necesaria para entrar en estado de transición disminuye, disminuyendo así la energía necesaria para iniciar la reacción.

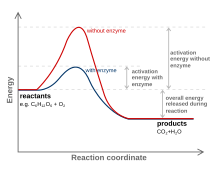
Una sustancia que modifica el estado de transición para reducir la energía de activación se denomina catalizador; un catalizador compuesto solo de proteína y (si corresponde) cofactores de molécula pequeña se denomina enzima. Un catalizador aumenta la velocidad de reacción sin consumirse en la reacción. Además, el catalizador reduce la energía de activación, pero no cambia las energías de los reactivos o productos originales, por lo que no cambia el equilibrio. Más bien, la energía del reactivo y la energía del producto siguen siendo las mismas y solo se altera (disminuye) la energía de activación.

Un catalizador puede reducir la energía de activación al formar un estado de transición de una manera más favorable. Los catalizadores, por naturaleza, crean un ambiente más "cómodo" adecuado para que el sustrato de una reacción progrese a un estado de transición. Esto es posible debido a la liberación de energía que ocurre cuando el sustrato se une al sitio activo de un catalizador. Esta energía se conoce como Binding Energy. Al unirse a un catalizador, los sustratos participan en numerosas fuerzas estabilizadoras mientras se encuentran dentro del sitio activo (p. ej., enlaces de hidrógeno o fuerzas de van der Waals). Se produce un enlace específico y favorable dentro del sitio activo hasta que se forma el sustrato para convertirse en el estado de transición de alta energía. La formación del estado de transición es más favorable con el catalizador porque las interacciones estabilizadoras favorables dentro del sitio activo liberan energía. Una reacción química puede fabricar una molécula de estado de transición de alta energía más fácilmente cuando hay un ajuste estabilizador dentro del sitio activo de un catalizador. La energía de enlace de una reacción es esta energía liberada cuando ocurren interacciones favorables entre el sustrato y el catalizador. La energía de enlace liberada ayuda a lograr el estado de transición inestable. Las reacciones sin catalizadores necesitan un mayor aporte de energía para alcanzar el estado de transición. Las reacciones no catalizadas no tienen energía libre disponible de las interacciones estabilizadoras del sitio activo, como las reacciones de enzimas catalíticas.

Relación con la energía de activación de Gibbs

En la ecuación de Arrhenius, el término energía de activación (E_a) se usa para describir la energía requerida para alcanzar el estado de transición y la relación exponencial k = A exp(−E_a/RT) se mantiene. En la teoría del estado de transición, se utiliza un modelo más sofisticado de la relación entre las velocidades de reacción y el estado de transición, una relación matemática superficialmente similar, la ecuación de Eyring, para describir la constante de velocidad de una reacción: k = (k_BT / h) exp(−Δ G^‡ / RT). Sin embargo, en lugar de modelar fenomenológicamente la dependencia de la temperatura de la velocidad de reacción, la ecuación de Eyring modela los pasos elementales individuales de una reacción. Por lo tanto, para un proceso de varios pasos, no existe una relación directa entre los dos modelos. Sin embargo, las formas funcionales de las ecuaciones de Arrhenius y Eyring son similares y, para un proceso de un solo paso, se pueden establecer correspondencias simples y químicamente significativas entre los parámetros de Arrhenius y Eyring.

En lugar de usar también E_a, la ecuación de Eyring usa el concepto de energía de Gibbs y el símbolo ΔG^‡ para indicar la energía de activación de Gibbs para lograr el estado de transición. En la ecuación, k_B y h son las constantes de Boltzmann y Planck, respectivamente. Aunque las ecuaciones parecen similares, es importante notar que la energía de Gibbs contiene un término entrópico además del entálpico. En la ecuación de Arrhenius, este término entrópico se explica por el factor preexponencial A. Más específicamente, podemos escribir la energía libre de activación de Gibbs en términos de entalpía y entropía de activación: ΔG^‡ = ΔH^‡ − T ΔS^‡. Entonces, para una reacción unimolecular de un paso, las relaciones aproximadas E_a = Δ H^‡ + RT y A = (k_BT/h) exp(1 + ΔS^‡ /R) mantener. Tenga en cuenta, sin embargo, que en la teoría de Arrhenius propiamente dicha, A es independiente de la temperatura, mientras que aquí existe una dependencia lineal de T. Para un proceso unimolecular de un solo paso cuya vida media a temperatura ambiente es de aproximadamente 2 horas, ΔG^‡ es de aproximadamente 23 kcal/mol. Esta es también la magnitud aproximada de E_a para una reacción que se desarrolla durante varias horas a temperatura ambiente. Debido a la magnitud relativamente pequeña de TΔS^‡ y RT a temperaturas ordinarias para la mayoría de las reacciones, en discurso, E_a, ΔG^‡, y ΔH ^‡ a menudo se combinan y todos se denominan "energía de activación".

La entalpía, la entropía y la energía de activación de Gibbs se escriben más correctamente como Δ^‡H^o, Δ^‡S^o y Δ^‡G^o respectivamente, donde la o indica una cantidad evaluada entre estados estándar. Sin embargo, algunos autores omiten la o para simplificar la notación.

Sin embargo, el cambio de energía libre total de una reacción es independiente de la energía de activación. Las reacciones físicas y químicas pueden ser exergónicas o endergónicas, pero la energía de activación no está relacionada con la espontaneidad de una reacción. El cambio total de energía de reacción no se ve alterado por la energía de activación.

Energía de activación negativa

En algunos casos, las velocidades de reacción disminuyen al aumentar la temperatura. Cuando se sigue una relación aproximadamente exponencial para que la constante de velocidad aún se pueda ajustar a una expresión de Arrhenius, esto da como resultado un valor negativo de E_a.

Las reacciones elementales que muestran energías de activación negativas suelen ser reacciones sin barreras, en las que el desarrollo de la reacción depende de la captura de las moléculas en un pozo de potencial. El aumento de la temperatura conduce a una probabilidad reducida de que las moléculas que colisionan se capturen entre sí (con más colisiones oblicuas que no conducen a una reacción, ya que el mayor momento lleva las partículas que chocan fuera del pozo de potencial), expresado como una sección transversal de reacción que disminuye con el aumento de la temperatura.. Tal situación ya no conduce a interpretaciones directas como el colmo de una barrera potencial.

Algunas reacciones de varios pasos también pueden tener energías de activación negativas aparentes. Por ejemplo, la constante de velocidad general k para una reacción de dos pasos A ⇌ B, B → C viene dada por k = k₂K₁, donde k ₂ es la constante de velocidad del segundo paso lento limitante de la velocidad y K₁ es la constante de equilibrio del primer paso rápido. En algunas reacciones, K₁ disminuye con la temperatura más rápidamente de lo que aumenta k₂, de modo que k realmente disminuye con la temperatura correspondiente a una energía de activación negativa observada.

Un ejemplo es la oxidación del óxido nítrico que es una reacción termolecular 2NO+O2→ → 2NO2{displaystyle 2NO+O_{2}rightarrow 2NO_{2}. The rate law is v=k[NO]2[O2]{displaystyle v=k,left[{rm {NO}right]cH00},left[{rm {c}}right] con una energía de activación negativa. Esto se explica por el mecanismo de dos pasos: 2NO▪ ▪ N2O2{displaystyle 2NOleftarrows N_{2}O_{2} y N2O2+O2→ → 2NO2{displaystyle ################################################################################################################################################################################################################################################################.

Ciertas reacciones de polimerización cónica tienen energías negativas de activación para que la tasa disminuya con temperatura. Para la polimerización de crecimiento de cadena, la energía de activación global es E=Ei+Ep− − Et{displaystyle textstyle E=E_{i}+E_{p}-E_{t}, donde i, p y t se refieren respectivamente a pasos de iniciación, propagación y terminación. El paso de propagación normalmente tiene una energía de activación muy pequeña, por lo que el valor global es negativo si la energía de activación para la terminación es mayor que la de iniciación. El rango normal de energías de activación global para la polimerización cationica varía de =40 a +60 kJ/mol.

Energía de activación en una superficie de energía potencial 2D

Estos son perfiles de PES para la reacción de gas de hidrógeno y tungsteno. El perfil de reacción en la izquierda muestra una vía dimensional del procedimiento. En el lado derecho se muestra una perspectiva de 1 dimensión de la misma trayectoria.

La energía de activación se puede representar en superficies de energía potencial (PES) 2D, donde la relación entre la geometría de los reactivos y la energía involucrada se representa como un mapa topográfico.

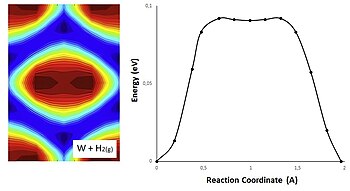
En el siguiente gráfico se representa una reacción entre el hidrógeno en fase gaseosa y un metal: el tungsteno. La energía potencial se obtiene con cálculos PES y es consistente con la posición de H de los cálculos del método NEB. Se puede utilizar una interpolación bidimensional con el método spline para evaluar la energía potencial en estas posiciones. Los productos y reactivos se pueden encontrar en la superficie azul, sin embargo, la superficie roja corresponde a la aproximación del estado estacionario.

Las representaciones corresponden a las trayectorias. Cuanto más azul es la superficie, más fuertes son los enlaces de hidrógeno, por lo que los colores azules representan la energía mínima y los colores rojos son los máximos. El PES de tungsteno es simétrico y tiene un hundimiento en el sitio del puente, este hundimiento corresponde al cambio de color en el centro de la imagen.

Cuanto más azul es la superficie entre los mínimos de energía, más bajas son las barreras de energía y, por lo tanto, más fácilmente viaja el hidrógeno a lo largo de las superficies.