Emisión espontánea

Emisión espontánea es el proceso en el que un sistema de mecánica cuántica (como una molécula, un átomo o una partícula subatómica) transita de un estado de energía excitado a un estado de menor energía (por ejemplo, su base estado) y emite una cantidad cuantificada de energía en forma de fotón. La emisión espontánea es en última instancia responsable de la mayor parte de la luz que vemos a nuestro alrededor; es tan omnipresente que se le dan muchos nombres a lo que es esencialmente el mismo proceso. Si los átomos (o moléculas) se excitan por algún medio que no sea el calor, la emisión espontánea se denomina luminiscencia. Por ejemplo, las luciérnagas son luminiscentes. Y existen diferentes formas de luminiscencia dependiendo de cómo se produzcan los átomos excitados (electroluminiscencia, quimioluminiscencia, etc.). Si la excitación se ve afectada por la absorción de radiación, la emisión espontánea se denomina fluorescencia. A veces, las moléculas tienen un nivel metaestable y continúan emitiendo fluorescencia mucho después de que se apaga la radiación excitante; esto se llama fosforescencia. Las figuras que brillan en la oscuridad son fosforescentes. Los láseres comienzan por emisión espontánea, luego, durante el funcionamiento continuo, funcionan por emisión estimulada.

La emisión espontánea no puede explicarse mediante la teoría electromagnética clásica y es fundamentalmente un proceso cuántico. Según la Sociedad Estadounidense de Física, la primera persona en predecir correctamente el fenómeno de la emisión espontánea fue Albert Einstein en una serie de artículos que comenzaron en 1916 y culminaron en lo que ahora se llama el Coeficiente A de Einstein. La teoría cuántica de la radiación de Einstein anticipó las ideas expresadas posteriormente en la electrodinámica cuántica y la óptica cuántica por varias décadas. Más tarde, después del descubrimiento formal de la mecánica cuántica en 1926, Dirac describió con precisión la tasa de emisión espontánea a partir de los primeros principios en su teoría cuántica de la radiación, el precursor de la teoría que más tarde llamó electrodinámica cuántica. Los físicos contemporáneos, cuando se les pide que den una explicación física para la emisión espontánea, generalmente invocan la energía de punto cero del campo electromagnético. En 1963, se desarrolló el modelo de Jaynes-Cummings que describe el sistema de un átomo de dos niveles que interactúa con un modo de campo cuantificado (es decir, el vacío) dentro de una cavidad óptica. Dio la predicción no intuitiva de que la tasa de emisión espontánea podría controlarse según las condiciones límite del campo de vacío circundante. Estos experimentos dieron lugar a la electrodinámica cuántica de cavidades (CQED), el estudio de los efectos de los espejos y las cavidades en las correcciones radiativas.

Introducción

Si una fuente de luz (el átomo) está en un estado excitado con energía E2{displaystyle E_{2}, puede decaer espontáneamente a un nivel de mentira inferior (por ejemplo, el estado del suelo) con energía E1{displaystyle E_{1}, liberando la diferencia de energía entre los dos estados como fotones. El foton tendrá frecuencia angular ⋅ ⋅ {displaystyle omega } y una energía ▪ ▪ ⋅ ⋅ {displaystyle hbar omega }:

E2− − E1=▪ ▪ ⋅ ⋅ ,{displaystyle E_{2}-E_{1}=hbar omega}

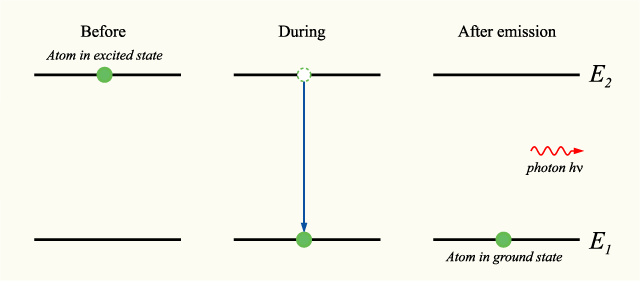
Donde ▪ ▪ {displaystyle hbar } es la constante de Planck reducido. Nota: ▪ ▪ ⋅ ⋅ =h.. {displaystyle hbar omega =hnu }, donde h{displaystyle h} es el Planck constante y .. {displaystyle nu } es la frecuencia lineal. La fase del fotón en emisión espontánea es al azar, como es la dirección en la que el fotón se propaga. Esto no es cierto para la emisión estimulada. A continuación se muestra un diagrama de nivel energético que ilustra el proceso de emisión espontánea:

Si el número de fuentes de luz en el estado excitado a la vez t{displaystyle t} es dado por N()t){displaystyle N(t)}, la tasa a la que N{displaystyle N} Decays es:

∂ ∂ N()t)∂ ∂ t=− − A21N()t),{displaystyle {frac {partial N(t)}{partial t}=-A_{21}N(t),}

Donde A21{displaystyle A_{21} es la tasa de emisión espontánea. En la ecuación de la tasa A21{displaystyle A_{21} es una proporcionalidad constante para esta transición particular en esta fuente de luz particular. La constante se conoce como la Einstein Un coeficiente, y tiene unidades s⁻¹. La ecuación anterior se puede resolver para dar:

N()t)=N()0)e− − A21t=N()0)e− − .. radt,{displaystyle N(t)=N(0)e^{-A_{21}t}=N(0)e^{-Gamma _{!{text{rad}}t}}}

Donde N()0){displaystyle N(0)} es el número inicial de fuentes de luz en el estado excitado, t{displaystyle t} es el tiempo y .. rad{displaystyle "Gamma" es la tasa de deterioro radiativo de la transición. El número de estados excitados N{displaystyle N} así decae exponencialmente con el tiempo, similar a la desintegración radiactiva. Después de una vida, el número de estados excitados se desintegra al 36,8% de su valor original (1e{displaystyle {frac {}{e}} {fn}} {fn}}} {fn}}} {fn}} {fn}}} {fn}}}}}}}} {fn}}}}}}-tiempo). La tasa de deterioro radiativo .. rad{displaystyle "Gamma" es inversamente proporcional a la vida τ τ 21{displaystyle tau _{21}:

A21=.. 21=1τ τ 21.{displaystyle A_{21}= Gamma ¿Qué?

Teoría

Las transiciones espontáneas no eran explicables en el marco de la ecuación de Schrödinger, en la que los niveles de energía electrónica estaban cuantificados, pero el campo electromagnético no. Dado que los estados propios de un átomo están correctamente diagonalizados, la superposición de las funciones de onda entre el estado excitado y el estado fundamental del átomo es cero. Por lo tanto, en ausencia de un campo electromagnético cuantificado, el átomo en estado excitado no puede decaer al estado fundamental. Para explicar las transiciones espontáneas, la mecánica cuántica debe extenderse a una teoría cuántica de campos, en la que el campo electromagnético se cuantifica en cada punto del espacio. La teoría cuántica de campos de electrones y campos electromagnéticos se conoce como electrodinámica cuántica.

En la electrodinámica cuántica (o QED), el campo electromagnético tiene un estado fundamental, el vacío QED, que puede mezclarse con los estados estacionarios excitados del átomo. Como resultado de esta interacción, el "estado estacionario" del átomo ya no es un verdadero estado propio del sistema combinado del átomo más el campo electromagnético. En particular, la transición del electrón del estado excitado al estado fundamental electrónico se mezcla con la transición del campo electromagnético del estado fundamental al estado excitado, un estado de campo con un fotón en él. La emisión espontánea en el espacio libre depende de las fluctuaciones del vacío para comenzar.

Aunque solo hay una transición electrónica del estado excitado al estado fundamental, hay muchas formas en las que el campo electromagnético puede pasar del estado fundamental al estado de un fotón. Es decir, el campo electromagnético tiene infinitamente más grados de libertad, correspondientes a las diferentes direcciones en las que se puede emitir el fotón. De manera equivalente, se podría decir que el espacio de fase que ofrece el campo electromagnético es infinitamente mayor que el que ofrece el átomo. Este infinito grado de libertad para la emisión del fotón da como resultado la aparente descomposición irreversible, es decir, la emisión espontánea.

En presencia de modos electromagnéticos de vacío, el sistema combinado átomo-vacío se explica por la superposición de las funciones de onda del átomo en estado excitado sin fotón y el átomo en estado fundamental con un único fotón emitido:

Silencio↑ ↑ ()t).. =a()t)e− − i⋅ ⋅ 0tSilencioe;0.. +.. k,sbks()t)e− − i⋅ ⋅ ktSilenciog;1ks.. {displaystyle ← (t)rangle =a(t)e^{-iomega ################################################################################################################################################################################################################################################################ ################################################################################################################################################################################################################################################################

Donde Silencioe;0.. {displaystyle Silencioso;0rangle } y a()t){displaystyle a(t)} son la atómica excitada función de onda de vacío estatal-electrognetica y su amplitud de probabilidad, Silenciog;1ks.. {displaystyle ← y bks()t){displaystyle b_{ks}(t)} son el átomo de estado del suelo con un solo fotón (de modo ks{displaystyle ks}) funcionamiento de onda y su amplitud de probabilidad, ⋅ ⋅ 0{displaystyle omega ¿Qué? es la frecuencia de transición atómica, y ⋅ ⋅ k=cSilenciokSilencio{displaystyle omega ¿Qué? es la frecuencia del fotón. La suma ha terminado. k{displaystyle k} y s{displaystyle s}, que son el número de onda y la polarización del fotón emitido, respectivamente. Como se mencionó anteriormente, el fotón emitido tiene la oportunidad de ser emitido con diferentes números de onda y polarizaciones, y la función de onda resultante es una superposición de estas posibilidades. Para calcular la probabilidad del átomo en el estado del suelo (Silenciob()t)Silencio2{displaystyle Silenciob(t)), uno necesita resolver la evolución del tiempo de la función de onda con un Hamiltonian apropiado. Para resolver por la amplitud de transición, se necesita un promedio de sobre (integrar sobre) todos los modos de vacío, ya que hay que considerar las probabilidades de que el fotón emitido ocupa diversas partes del espacio de fase por igual. El fotón emitido "espontáneo" tiene modos infinitamente diferentes para propagarse, por lo que la probabilidad de que el átomo reabsorbe el fotón y regrese al estado original es insignificante, haciendo la caries atómica prácticamente irreversible. Tal evolución temporal irreversible del sistema atom-vacuum es responsable de la aparente decadencia espontánea de un átomo excitado. Si uno tuviera que hacer un seguimiento de todos los modos de vacío, el sistema combinado atom-vacuum pasaría por la evolución del tiempo unitario, haciendo reversible el proceso de desintegración. Cavity quantum electrodynamics es uno de esos sistemas donde los modos de vacío se modifican resultando en el proceso de decadencia reversible, vea también Quantum revival. La teoría de la emisión espontánea bajo el marco QED fue calculada primero por Weisskopf y Wigner.

Tasa de emisión espontánea

La tasa de emisión espontánea (es decir, la tasa de radiación) puede describirse mediante la regla de oro de Fermi. La tasa de emisión depende de dos factores: una 'parte atómica', que describe la estructura interna de la fuente de luz y una 'parte de campo', que describe la densidad de los modos electromagnéticos del entorno. La parte atómica describe la fuerza de una transición entre dos estados en términos de momentos de transición. En un medio homogéneo, como el espacio libre, la tasa de emisión espontánea en la aproximación dipolar viene dada por:

.. rad()⋅ ⋅ )=⋅ ⋅ 3nSilencioμ μ 12Silencio23π π ε ε 0▪ ▪ c3=4α α ⋅ ⋅ 3nSilencio.. 1SilenciorSilencio2.. Silencio23c2{displaystyle Gamma _{text{rad}}(omega)={frac {omega ^{3}n durablemu ¿Qué? varepsilon ################################################################################################################################################################################################################################################################

Silencioμ μ 12Silencio2π π ε ε 0▪ ▪ c=4α α Silencio.. 1SilenciorSilencio2.. Silencio2{displaystyle {frac {fnMicroc} ¿Qué? varepsilon #4alpha Silenciolangle 1 muertemathbf {r}

Donde ⋅ ⋅ {displaystyle omega } es la frecuencia de emisión, n{displaystyle n} es el índice de refracción, μ μ 12{displaystyle mu _{12}} es el momento de la transición dipole, ε ε 0{displaystyle varepsilon ¿Qué? es la autorización de vacío, ▪ ▪ {displaystyle hbar } es la reducción Planck constante, c{displaystyle c} es la velocidad de vacío de la luz, y α α {displaystyle alpha } es la constante de buena estructura. La expresión Silencio.. 1SilenciorSilencio2.. Silencio{fnMicrosoft Sans Serif} Silencio. significa la definición del momento del dipolo de transición Silencioμ μ 12Silencio=Silencio.. 1SilenciodSilencio2.. Silencio{fnMicrosoft Sans Serif} _{12} Silencio. para operador de momento dipole d=qr{displaystyle mathbf {d} =qmathbf {r}, donde q{displaystyle q} es la carga primaria y r{displaystyle mathbf {r} significa operador de posición. (Esta aproximación se descompone en el caso de electrones de cáscara interior en átomos de alta Z.) La ecuación anterior muestra claramente que la tasa de emisión espontánea en el espacio libre aumenta proporcionalmente a ⋅ ⋅ 3{displaystyle omega ^{3}.

En contraste con los átomos, que tienen un espectro de emisión discreto, los puntos cuánticos se pueden ajustar continuamente cambiando su tamaño. Esta propiedad se ha utilizado para comprobar ⋅ ⋅ 3{displaystyle omega ^{3}- dependencia de frecuencias de la tasa de emisión espontánea descrita por la regla de oro de Fermi.

Desintegración radiativa y no radiativa: la eficiencia cuántica

En la ecuación de tasas arriba, se supone que la decadencia del número de estados excitados N{displaystyle N} sólo ocurre bajo emisión de luz. En este caso se habla de decaimiento radiativo completo y esto significa que la eficiencia cuántica es 100%. Además de la desintegración radiativa, que ocurre bajo la emisión de luz, hay un segundo mecanismo de desintegración; la desintegración no radiativa. Determinar la tasa total de desintegración .. Tot{displaystyle "Gamma", las tasas radiativas y no radiativas deben resumirse:

.. Tot=.. rad+.. nrad{displaystyle "Gamma" Gamma...

Donde .. Tot{displaystyle "Gamma" es la tasa total de desintegración, .. rad{displaystyle "Gamma" es la tasa de deterioro radiativo y .. nrad{displaystyle "Gamma" la tasa de desintegración no radiativa. La eficiencia cuántica (QE) se define como la fracción de los procesos de emisión en los que la emisión de luz está implicada:

QE=.. rad.. nrad+.. rad.{displaystyle {text{QE}={frac} {fnMicrosoft Sans Serif} {fnMicrosoft Sans Serif} {fnMicrosoft Sans Serif}} {\fnMicrosoft Sans Serif}} {fnMicrosoft Sans Serif} {fnMicrosoft Sans Serif} Gamma _{text{nrad}+ Gamma - ¿Qué?

En la relajación no radiativa, la energía se libera en forma de fonones, más comúnmente conocida como calor. La relajación no radiativa se produce cuando la diferencia de energía entre los niveles es muy pequeña y, por lo general, se produce en una escala de tiempo mucho más rápida que las transiciones radiativas. Para muchos materiales (por ejemplo, semiconductores), los electrones se mueven rápidamente desde un nivel de alta energía a un nivel metaestable a través de pequeñas transiciones no radiativas y luego hacen el movimiento final hacia el nivel inferior a través de una transición óptica o radiativa. Esta transición final es la transición sobre la banda prohibida en los semiconductores. Las grandes transiciones no radiativas no ocurren con frecuencia porque la estructura cristalina generalmente no puede soportar grandes vibraciones sin destruir los enlaces (lo que generalmente no sucede con la relajación). Los estados metaestables forman una característica muy importante que se explota en la construcción de láseres. Específicamente, dado que los electrones se descomponen lentamente, se pueden apilar deliberadamente en este estado sin demasiada pérdida y luego se puede usar la emisión estimulada para aumentar una señal óptica.