Elipse

Ajustar Compartir Imprimir Citar

Un elipse (rojo) obtenido como la intersección de un cono con un plano inclinado.

Elipse: notaciones

Elipses: ejemplos con creciente excentricidad

En matemáticas, un elipse es una curva de plano que rodea dos puntos focales, tal que para todos los puntos de la curva, la suma de las dos distancias a los puntos focales es una constante. Generaliza un círculo, que es el tipo especial de elipse en el que los dos puntos focales son los mismos. La elongación de una elipse se mide por su excentricidad ${displaystyle e}$ , un número que va desde ${displaystyle e=0}$ (el caso límite de un círculo) a ${displaystyle e=1}$ (el caso limitante de la elongación infinita, ya no es una elipse sino una parabola).

Una elipse tiene una solución algebraica simple para su área, pero solo aproximaciones para su perímetro (también conocido como circunferencia), para lo cual se requiere integración para obtener una solución exacta.

Analíticamente, la ecuación de un elipse estándar centrado en el origen con ancho ${displaystyle 2a}$ y altura ${displaystyle 2b}$ es:

{fnMicroc} {x^{2}{a^{2}}+{frac} {y^{2}{b^{2}}=1.}

Sumas ${displaystyle ageq b}$ , el foci son ${displaystyle (pm c,0)}$ para ${textstyle c={sqrt {a^{2}-b^{2}}}$ . La ecuación paramétrica estándar es:

{displaystyle (x,y)=(acos(t),bsin(t))quad {text{for}quad 0leq tleq 2pi.}

Las elipses son el tipo cerrado de sección cónica: una curva plana que traza la intersección de un cono con un plano (ver figura). Las elipses tienen muchas similitudes con las otras dos formas de secciones cónicas, parábolas e hipérbolas, las cuales son abiertas e ilimitadas. Una sección transversal en ángulo de un cilindro también es una elipse.

Una elipse también se puede definir en términos de un punto focal y una línea fuera de la elipse denominada directriz: para todos los puntos de la elipse, la relación entre la distancia al foco y la distancia a la directriz es una constante. Esta relación constante es la excentricidad antes mencionada:

{displaystyle e={frac {c}{a}={sqrt {1-{frac {B^{2}}}}}}}

Las elipses son comunes en física, astronomía e ingeniería. Por ejemplo, la órbita de cada planeta del Sistema Solar es aproximadamente una elipse con el Sol en un punto focal (más precisamente, el foco es el baricentro del par Sol-planeta). Lo mismo es cierto para las lunas que orbitan planetas y todos los demás sistemas de dos cuerpos astronómicos. Las formas de los planetas y las estrellas suelen estar bien descritas por elipsoides. Un círculo visto desde un ángulo lateral parece una elipse: es decir, la elipse es la imagen de un círculo bajo una proyección paralela o en perspectiva. La elipse es también la figura de Lissajous más simple que se forma cuando los movimientos horizontal y vertical son sinusoides con la misma frecuencia: un efecto similar conduce a la polarización elíptica de la luz en la óptica.

El nombre, ἔλλειψις (élleipsis, "omisión"), fue dada por Apolonio de Perge en sus Cónicas.

Definición como lugar geométrico de los puntos

Elipse: definición por suma de distancias a foci

Elipse: definición por enfoque y directrix circular

Una elipse se puede definir geométricamente como un conjunto o lugar geométrico de puntos en el plano euclidiano:

Dados dos puntos fijos ${displaystyle F_{1},F_{2}$ llamada foci y una distancia ${displaystyle 2a}$ que es mayor que la distancia entre el foci, el elipse es el conjunto de puntos ${displaystyle P}$ tal que la suma de las distancias ${fnMicrosoft Sans Serif}$ es igual a ${displaystyle 2a}$ : ${displaystyle E=left{Pin mathbb {R} ^{2},mid , WordPressPF_{2}Sobrevivir=2aright}}$

El punto medio ${displaystyle C}$ del segmento de línea que une el foci se llama centro de la elipse. La línea a través de la foci se llama eje principal, y la línea perpendicular a él a través del centro es el eje menor. El eje principal interseca el elipse en dos vertices ${displaystyle V_{1},V_{2}$ , que tienen distancia ${displaystyle a}$ al centro. La distancia ${displaystyle c}$ del foci al centro se llama el distancia focal o excentricidad lineal. El cociente ${displaystyle e={tfrac {c}{a}}$ es excentricidad.

El caso ${displaystyle F_{1}=F_{2}$ produce un círculo y se incluye como un tipo especial de elipse.

La ecuación ${displaystyle Silencio.$ se puede ver de una manera diferente (véase la figura):

Si ${displaystyle c_{2}$ es el círculo con el centro ${displaystyle F_{2}$ y radio ${displaystyle 2a}$ , entonces la distancia de un punto ${displaystyle P}$ al círculo ${displaystyle c_{2}$ iguala la distancia al foco ${displaystyle F_{1}$ :
${displaystyle Silencio.$

${displaystyle c_{2}$ se llama circular directrix (relacionado con la concentración ${displaystyle F_{2}$ De la elipse. Esta propiedad no debe confundirse con la definición de un elipse utilizando una línea directrix a continuación.

Usando esferas de Dandelin, se puede demostrar que cualquier sección de un cono con un plano es una elipse, asumiendo que el plano no contiene el vértice y tiene una pendiente menor que la de las líneas del cono.

En coordenadas cartesianas

Parámetros de forma:
a: eje semi-major,
b: semi-minor axis,
c: excentricidad lineal,
p: semi-latus recto (normalmente ${displaystyle ell }$ ).

Ecuación estándar

La forma estándar de una elipse en coordenadas cartesianas supone que el origen es el centro de la elipse, el eje x es el eje mayor y:

los puntos ${displaystyle F_{1}=(c,,0), F_{2}=(-c,,0)}$ ,

los vértices son ${displaystyle V_{1}=(a,,0), V_{2}=(-a,�)}$ .

Para un punto arbitrario ${displaystyle (x,y)}$ la distancia al foco ${displaystyle (c,0)}$ es ${fnMicrosoft Sans Serif}}$ y al otro enfoque ${fnMicrosoft Sans Serif}}$ . Por lo tanto el punto ${displaystyle (x,,y)}$ está en el elipse cuando:

${fnMicrosoft Sans Serif}+ {fnMicrosoft Sans Serif} {fnMicrosoft Sans Serif}}}}=2a.}$

Eliminación de los radicales por squarings adecuados y utilizando ${displaystyle - Sí.$ (ver diagrama) produce la ecuación estándar de la elipse:

${fnMicroc} {x^{2}{a^{2}}+{frac} {y} {y} {y} {y}} {y} {y}} {y}} {}} {}} {}} {}}}} {}}}}} {}}} {}}}} {}}} {}}}}} {}}} {}}}}}}} {}}}}}}}} {}}}}} {}}}}}} {}}}}}}}}} {}}}}}}}}}}} {}}} {}}}}}}}}}} {}}}}}}} {}}}}} {}}}}} {}}}}}}}}}}}}} {} {}}}}}}}} {} {}}}} {}}}}}}}}}}}}}}} {}}}}}}}}}}}} {}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}$

o, resuelto para y:

${displaystyle y=pm {frac {b}{a}{sqrt {a^{2}-x^{2}}=pm {sqrt {left(a^{2}-x^{2}right)left(1-e^{2}}}}}}$

Parámetros de ancho y altura ${displaystyle a,;b}$ se llaman los ejes semi-major y semi-minor. Los puntos de arriba y abajo ${displaystyle V_{3}=(0,,b),;V_{4}=(0,,-b)}$ son co-vertices. Las distancias desde un punto ${displaystyle (x,,y)}$ en la elipse a la izquierda y derecha foci son ${displaystyle a+ex}$ y ${displaystyle a-ex}$ .

Se deduce de la ecuación que la elipse es simétrica con respecto a los ejes de coordenadas y, por lo tanto, con respecto al origen.

Parámetros

Ejes principales

A lo largo de este artículo, los ejes semi-major y semi-minor son denotados ${displaystyle a}$ y ${displaystyle b}$ , respectivamente, es decir. ${fnMicrosoft Sans Serif}$

En principio, la ecuación de elipse canónica ${fnMicroc} {x^{2}{a^{2}}+{tfrac {y} {y}{b^{2}}=1}$ puede haber ${displaystyle a meantb}$ (y por lo tanto el elipse sería más alto de lo ancho). Este formulario se puede convertir a la forma estándar transponiendo los nombres variables ${displaystyle x}$ y ${displaystyle y}$ y los nombres del parámetro ${displaystyle a}$ y ${displaystyle b.}$

Excentricidad lineal

Esta es la distancia del centro a un enfoque: ${displaystyle c={sqrt {a^{2}-b^{2}}}$ .

Excentricidad

La excentricidad se puede expresar como:

${displaystyle e={frac {c}{a}={2}}}}$

suposición ${displaystyle a prendab.}$ Un elipse con ejes iguales ( ${displaystyle a=b}$ ) tiene cero excentricidad, y es un círculo.

Recto semilato

La longitud del acorde a través de un enfoque, perpendicular al eje mayor, se llama el el recto. Una mitad es la semi-latus recto ${displaystyle ell }$ . Un cálculo muestra:

${displaystyle ell ={frac {b^{2}{a}=aleft(1-e^{2}right).}$

El recto semi-latus ${displaystyle ell }$ es igual al radio de curvatura en los vértices (ver curvatura sección).

Tangente

Una línea arbitraria ${displaystyle g}$ interseca un elipse a 0, 1, o 2 puntos, respectivamente llamado exterior, tangente y secant. A través de cualquier punto de una elipse hay un tangente único. El tangente en un punto ${displaystyle (x_{1},,y_{1}}$ de la elipse ${fnMicroc} {x^{2}{a^{2}}+{tfrac {y} {y}{b^{2}}=1}$ tiene la ecuación de coordenadas:

${fnMicroc} {x_{1}{a}}x+{frac} Sí.$

Una ecuación vectorial paramétrica de la tangente es:

${displaystyle {vec {x}={begin{pmatrix}x_{1}y_{1}end{pmatrix}}+s{begin{pmatrix};!-y_{1}a^{2}\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\]\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\ x_{1}b^{2}end{pmatrix}$ con ${displaystyle sin mathbb {R} .}$

Prueba:Vamos ${displaystyle (x_{1},,y_{1}}$ ser un punto en una elipse y ${fnfnMicrosoft {fnMicrosoft {fnMicrosoft {fnMicrosoft {fnMicrosoft {\fnMicrosoft {\fnMicrosoft {fnMicrosoft {fnMicrosoft {\fnMicrosoft {\fnMicrosoft {\fnMicrosoft {\\\fnMicrosoft}\\\\\\\\fnMicrosoft\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\ {x}={begin{pmatrix}x_{1}y_{1}end{pmatrix}}+s{begin{pmatrix}uvend{pmatrix}}}}} {c}} {c}}}} {ccc}}}}}}}}} {cc}}}}}}}}}}}}}}}}}}}}}} {ccc}}}}}}}}}} {cccccccccccccc}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}cccccccccccccccccccccccccccccc$ ser la ecuación de cualquier línea ${displaystyle g}$ que contiene ${displaystyle (x_{1},,y_{1}}$ . Insertar la ecuación de la línea en la ecuación del elipse y respetar ${fnMicroc} {x_{1} {2}{a^{2}}}+{frac} {f} {f}} {f}}} {f}}}} {f}}}} {f}}}} {f}}} {f}}}} {f}}} {f}}}}}}}}}}}}}}}}}}} { {y_{1} {2}{b} {2}}=1}} {c}}} {c}}}} {c}}}}}}}}}}} {c}}}}}}}}}}}}}} {c}}}}}}}}}}}}}}} {c}} {}}}}}}}}}}} {}}}}}}}}}}}}}}}}} {}}}}}}}}}}}}}}}}}}}}}}}}}}} {}}}}}}}}}}}}}}}}}}}}}}}} {}}}}}}}}}}}}}}}}}} {}}}}}}}}}}}}}}}}}}}}}}}}} {}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}$ rendimientos:

${displaystyle {frac {left(x_{1}+suright)}{2}{a^{2}}}}+{frac {left(y_{1}+svright)}{2}{b^{2}}}=1quad Longrightarrow quad 2sleft({frac}{frac}}}}}{2}}}}}}}}}=1qqqqqqq}}}}}}}}}}}}}}=1qqqqqqqqqqqqqqq\qqqqqqqq\\qq\\\qqqq\\q\\\\\qqqq\qqq\qq\q\ {x_{1}u}{2}}+{frac} {y_{1}v}{b^{2}}}derecha)+s^{2}left({frac} {fnMicroc} {fnMicroc}}} {fnMicroc}}} {f}}}} {f}} {fn}}}}}}} {f}}} {fnMicroc} {fnMicrosoft Sans Serif} {fnMicrosoft Sans Serif}$

Hay entonces casos:

${fnMicroc} {x_{1}{a^{2}}u+{frac} - ¿Qué?$ Entonces línea ${displaystyle g}$ y el elipse tienen sólo punto ${displaystyle (x_{1},,y_{1}}$ en común, y ${displaystyle g}$ es un tangente. La dirección tangente tiene vector perpendicular ${displaystyle {begin{pmatrix}{frac} {x_{1}{2} {f}} {f}} {f}}} {f}} {f}}} {f}} {f}}}}} {f}}}}} {f}}}} {f}}}}} {f}}}}}}}} {f}}}}}}}}}}}}}}}} {f}}}}}}}}}}}} {f}} {f}}} {f}}} {f}}}}}}} {f}}} {f}}} {f}}}}}}}}}}} {f}}}}}}}}}}}}}}}}}} {f}}}}}}}}}}}}}} {f}}} {f}}} {f}}}}}}}} {f}}}}}}}}}}}}}}}}}}}}}} {y_{1}{b^{2}}end{pmatrix}} {f}}} {f}}} {f}}} {f}}}}}}}}} {f}}}}}}}} {f}}}}}}}}}}}}}}}}}}} {f}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}$ , por lo que la línea tangente tiene ecuación ${textstyle {frac {x_{1}{2}x+{tfrac} Sí.$ para algunos ${displaystyle k}$ . Porque... ${displaystyle (x_{1},,y_{1}}$ está en el tangente y la elipse, se obtiene ${displaystyle k=1}$ .
${fnMicroc} {x_{1}{a^{2}}u+{frac} {y_{1} {b^{2}}vneq 0.}$ Entonces línea ${displaystyle g}$ tiene un segundo punto en común con la elipse, y es un secant.

Usando (1) uno encuentra que ${displaystyle {begin{pmatrix}-y_{1}a^{2} {2}b^{2}end{pmatrix}}}$ es un vector tangente en el punto ${displaystyle (x_{1},,y_{1}}$ , que demuestra la ecuación vectorial.

Si ${displaystyle (x_{1},y_{1}}$ y ${displaystyle (u,v)}$ son dos puntos de la elipse tal que ${textstyle {frac {x_{1}u}{2}}+{tfrac {y_{1}v}{b^{2}}=0}$ , entonces los puntos se encuentran en dos diámetros conjugados (véase infra). (Si) ${displaystyle a=b}$ , el elipse es un círculo y "conjugar" significa "ortogonal".)

Elipse desplazada

Si el elipse estándar se cambia para tener centro ${displaystyle left(x_{circ },,y_{circ }right)}$ , su ecuación es

${displaystyle {frac {left(x-x_{circ }right)}{2}{a^{2}}}}+{frac {left(y-y-y_{circ }right)}{2}{b^{2}}}}=1}}}$

Los ejes siguen siendo paralelos a los ejes x e y.

Elipse general

En la geometría analítica, la elipse se define como un quadric: el conjunto de puntos ${displaystyle (X,,Y)}$ del plano cartesiano que, en casos no degenerados, satisfacen la ecuación implícita

${displaystyle AX^{2}+BXY+CY^{2}+DX+EY+F=0}$

proporcionadas ${displaystyle B^{2}-4AC 0}$

Para distinguir los casos degenerados de los casos no degenerados, sea ∆ el determinante

${displaystyle Delta ={begin{bmatrix}A paciente{frac {1}{2}Biéndose {frac} {1}{2}D\\\\fnMicroc {1}{2} {1}{2}E\{fnMic} {1}{2}D diez {frac} {1}{2}}E pacienteFend{bmatrix}=left(AC-{frac} F+{frac {BED}-{4}} {frac {frac}} {frac {f}{4}}} {frac {f} {f}} {fnMicroc}}}}}} {fnMicroc}}}} {f}}} {fnMicroc} {f}}}}}}}} {f}} {f}}}}}}}}} {f}}}}}}}}} {f} {f}}}}}} {f}}}} {f}}}}}} {f}}}}}}}}} {f}}}}}}}}}}}}}}}} {f}}}}}}}}}} {f}}}}}}}}}} {f}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}$

Entonces la elipse es una elipse real no degenerada si y solo si C∆ < 0. Si C∆ > 0, tenemos una elipse imaginaria, y si ∆ = 0, tenemos una elipse de puntos.

Los coeficientes de la ecuación general se pueden obtener a partir del eje semi-major conocido ${displaystyle a}$ , eje semi-minor ${displaystyle b}$ , coordenadas centrales ${displaystyle left(x_{circ },,y_{circ }right)}$ , y ángulo de rotación ${displaystyle theta }$ (el ángulo desde el eje horizontal positivo hasta el eje mayor del elipse) usando las fórmulas:

${displaystyle {begin{aligned}A limit=a^{2}sin ^{2}theta +b^{2}cos ^{2}theta \B implica=2left(b^{2}-a^{2}right)sin theta cos theta 'C paciente=a^{2}cos ^{2}theta ################################################################################################################################################################################################################################################################ ################################################################################################################################################################################################################################################################ }-By_{circ }E paciente=-Bx_{circ }-2Cy_{circ }\fnuncio=Ax_{circ ################################################################################################################################################################################################################################################################ }+Cy_{circ } {2}-a^{2}b^{2}$

Estas expresiones pueden derivarse de la ecuación canónica ${fnMicroc} {x^{2}{a^{2}}+{tfrac {y} {y}{b^{2}}=1}$ por una transformación afinada de las coordenadas ${displaystyle (x,,y)}$ :

${displaystyle {begin{aligned}x limit=left(X-x_{circ }right)cos theta +left(Y-y_{circ }right)sin theta \y viviendo=-left(X-x_{circ }right)sin theta +left(Y-y_{circ }right)cos theta.end{aligned}$

Por el contrario, los parámetros de forma canónica se pueden obtener a partir de los coeficientes de forma general mediante las ecuaciones:

${displaystyle {begin{aligned}a,b sentimiento={frac} {cHFF} {2{2}_Big (}AE^{2}+CD^{2}-BDE+(B^{2}-4AC)F{Big)}left(A+C)pm {sqrt {(A-C)^{2}+B^{2}}}}}}}}}}{2}-4AC}\\2}{2}{2}{2}{2}{}}}}}}}}}}}{2}}}}}}}{2}}}}}}}}}}}}}}}{2}}}}} {}}}}}}}}}}}}}}}}}{2}}}}} {c} {c} {c}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}} {c}}}}}}}}}}}}}}}}}}}}}}} { {2AE-BD}{2}[3pt]theta >{begin{cases}arctan left({frac] {1} {B}left(C-A-{sqrt {(A-C)^{2}+B^{2}}}}right)}{text{for }Bneq 0�}{�}B=0, UNA SEGUNDA C90}{�}{0}}}}}B=0}}$

Representación paramétrica

La construcción de puntos basados en la ecuación paramétrica y la interpretación del parámetro t, que se debe a de la Hire

Puntos de elipse calculados por la representación racional con parámetros espaciados iguales ( ${displaystyle Delta u=0.2}$ ).

Representación paramétrica estándar

Utilizando funciones trigonométricas, una representación paramétrica de la elipse estándar ${fnMicroc} {x^{2}{a^{2}}+{tfrac {y} {y}{b^{2}}=1}$ es:

${displaystyle (x,,y)=(acos t,,bsin t), 0leq t made2pi .}$

El parámetro t (llamado el anomalía excéntrica en la astronomía) no es el ángulo de ${displaystyle (x(t),y(t)}$ con el x-eje, pero tiene un significado geométrico debido a Philippe de La Hire (ver Dibujo elipses infra).

Representación racional

Con la sustitución ${textstyle u=tan left({frac {t}right)}$ y fórmulas trigonométricas que uno obtiene

${displaystyle cos t={frac {1-u^{2}{1+u^{2}}\quad sin t={frac} {f} {f}}}}\f2}}}\\\\\\\\\\q\\\\\\\\fnK\f}\f}\\\\\\\\f}\\\\\\\\\\f}\\\\\\\\\\f}\\\\\\\\\\\\\\fn\\\\\\fn\\\\\\fn\\\\\\\\\\\\fn\\\\ {2u}{1+u^{2}}}$

y la ecuación paramétrica racional de una elipse

${displaystyle {begin{aligned}x(u) {1-u^{2}{1+u^{2}\[10mu]y(u) {2u}{1+u^{2}}end{aligned};,quad -infty - {0}inftyinfty;}$

que cubre cualquier punto de la elipse ${fnMicroc} {x^{2}{a^{2}}+{tfrac {y} {y}{b^{2}}=1}$ excepto el vértice izquierdo ${displaystyle (-a,,0)}$ .

Para ${displaystyle uin [0,,1],}$ esta fórmula representa el cuarto superior derecho de la contra-auricular elipse con aumento ${displaystyle u.}$ El vértice izquierdo es el límite ${textstyle lim _{uto pm infty }(x(u),,y(u))=(-a,,0);.}$

Alternately, if the parameter ${displaystyle [u:v]}$ se considera un punto en la línea de proyecto real ${textstyle mathbf {P} (mathbf {R})}$ , entonces la parametrización racional correspondiente es

${displaystyle [u:v]mapsto left(a{frac] ¿Qué?$

Entonces... ${textstyle [1:0]mapsto (-a,,0). }$

Las representaciones racionales de las secciones cónicas se usan comúnmente en el diseño asistido por computadora (consulte la curva de Bezier).

Pendiente tangente como parámetro

Una representación paramétrica, que utiliza la pendiente ${displaystyle m}$ del tangente en un punto de la elipse puede obtenerse del derivado de la representación estándar ${fnMicrosoft Sans Serif}$ :

${displaystyle {vec {x}'(t)=(-asin t,bcos t)^{mathsf {T}}quad rightarrow quad m=-{frac {b}cot tquad rightarrow quad cot t=-{frac}{frac} {f} {f}f}f}f}f}f}f}f}f}f}f}f}f}f}f}f}f}f}f}f}f}f}f}f}f}f}f}f}f}f}f}f}f}f}f}f}f}f}f}f}f}f}f}f}f}fnh00f}f}f}f}f}f}f} {ma}{b}.}$

Con ayuda de fórmulas trigonométricas se obtiene:

${displaystyle cos t={frac {cot t}{pm {sqrt {1+cot ^{ 2}}={frac {-ma}{pm {sqrt {m^{2}a^{2}+b^{2}}quad quad sin t={frac {1}{pm {cHFF} {1+cot ^{ 2}}={frac {b}{2}}}}}$

Replacing ${displaystyle cos t}$ y ${displaystyle sin t}$ de los rendimientos de representación estándar:

${fnMicrosoft Sans Serif} {fnMicrosoft Sans Serif} {fnMicroc {fnMicroc} {fnMicroc} {fnMicroc} {fnMicrosoft}}{fnMicros}} {fnMicros}} {fnMicrosoft Principiciones}}f}f}}fncipiciones {sqrt {m^{2}a}{2}}}}};{frac {b^{2}}{pm {sqrt {m^{2}}}derecha),,min mathbb {R}$

Aquí. ${displaystyle m}$ es la pendiente del tangente en el punto de elipse correspondiente, ${displaystyle {vec {c}_{+}$ es la parte superior y ${displaystyle {vec {c}_{-}$ la mitad inferior de la elipse. Los vértices ${displaystyle (pm a,,0)}$ , teniendo tangentes verticales, no están cubiertos por la representación.

La ecuación del tangente en el punto ${fnMicrosoft Sans Serif}$ tiene la forma ${displaystyle Y=mx+n}$ . El todavía desconocido ${displaystyle n}$ puede determinarse insertando las coordenadas del punto de elipse correspondiente ${fnMicrosoft Sans Serif}$ :

${displaystyle y=mxpm { sqrt {m^{2}a^{2}+b^{2}};$

Esta descripción de las tangentes de una elipse es una herramienta esencial para la determinación de la ortóptica de una elipse. El artículo ortóptico contiene otra prueba, sin cálculo diferencial ni fórmulas trigonométricas.

Elipse general

Elipse como imagen afinada del círculo de la unidad

Otra definición de una elipse utiliza transformaciones afines:

Cualquier elipse es una imagen afinada del círculo de unidad con ecuación ${displaystyle x^{2}+y^{2}=1}$ .

Representación paramétrica

Una transformación afinada del plano Euclideano tiene la forma ${displaystyle {vec {x}mapsto {vec} {f}fnMicrosoft Sans Serif} {x}}$ , donde ${displaystyle A}$ es una matriz regular (con no cero determinante) y ${displaystyle {vec {f}f}}} {f}} {f}} {f}} {f}} {f}}}}} {f}}}}} {f}}}}} {f}}}}}} {f}}}}}}}} {f}f}}}}}}}}}}}}}$ es un vector arbitrario. Si ${displaystyle {vec {f}f}fnMicrosoft Sans Serif} {f}_{2}$ son los vectores de columna de la matriz ${displaystyle A}$ , el círculo de unidad ${displaystyle (cos(t),sin(t)}$ , ${displaystyle 0leq tleq 2pi}$ , se mapea en el elipse:

${displaystyle {vec}={vec} {p}(t)={vec {f}fnMicrosoft Sans {f}_{1}cos ¡T+{vec {f}f}cH00}fncipi} t.}$

Aquí. ${displaystyle {vec {f}f}}} {f}} {f}} {f}} {f}} {f}}}}} {f}}}}} {f}}}}} {f}}}}}} {f}}}}}}}} {f}f}}}}}}}}}}}}}$ es el centro y ${displaystyle {vec {f}f}fnMicrosoft Sans Serif} {f}_{2}$ son las direcciones de dos diámetros conjugados, en general no perpendicular.

Vertices

Los cuatro vértices de la elipse son ${displaystyle {vec {}(t_{0}),;{vec {p}left(t_{0}pm {tfrac {pi} }{2}right),;{vec {p}left(t_{0}+piright)}$ , para un parámetro ${displaystyle t=t_{0}$ definida por:

${displaystyle cot(2t_{0})={frac {{vec {f}fnMicrosoft Sans Serif} {f}f} {fnMicrosoft Sans Serif} {fnMicrosoft Sans Serif} {f} {f} {f} {f}} {f}f}f} {f} {f}f} {f}f}f} {f}f}f}f} {f}f}}}}}f}f}f}f}f}f}f}f}f}f}f}f}f}f}f}}\\\\\\f}f}}}}\\\\\\\\\\\\\\\\\\\f}f}}}}}f}}}}}}}}}}f}}}}}\\\\f}}}}}}}f} {f}_{1}cdot {f}f} {f}}}}$

(Si) ${displaystyle {vec}cdot} {fnMicrosoft Sans Serif}$ , entonces ${displaystyle T_{0}=0}$ .) Esto se deriva de la siguiente manera. El vector tangente en punto ${displaystyle {vec}(t)}$ es:

${fnMicrosoft Sans Serif},'(t)=-{vec {f}\fnMicrosoft Sans Serif} - ¿Por qué?$

En un parámetro de vértice ${displaystyle t=t_{0}$ , el tangente es perpendicular a los ejes principales / menores, por lo que:

${displaystyle 0={vec {}(t)cdot left({vec {p}(t)-{vec {f}}!_{0}right)=left(-{vecvec} {f}\fnMicrosoft Sans Serif} t+{vec {f}!_{2}cos tright)cdot left({vec {f}!_{1}cos t+{vec {f}!_{2}sin tright). }$

Ampliación y aplicación de las identidades ${displaystyle ;cos ^{2}t-sin ^{2}t=cos 2t, 2sin tcos t=sin 2t;}$ da la ecuación para ${displaystyle t=t_{0};.}$

Zona

Desde el teorema de Apolonios (ver abajo) se obtiene:
El área de un elipse ${displaystyle;{vec}={vec} {f}_{0}+{vec} {f}_{1}cos ##### {f} {f}sin t;}$ es

${displaystyle A=pi Silenciodet({vec {f}_{1},{vec {f}_{2})$

Semiaxes

Con las abreviaturas ${displaystyle ;M={vec {f}_{2}+{vec} {f}_{2} {2}, N=left upondet({vec {f}_{1},{vec {f}_{2})justo de la vida}$ las declaraciones del teorema de Apolonios pueden ser escritas como:

${displaystyle a^{2}+b^{2}=M,quad ab=N.}$

Resolver este sistema no lineal ${displaystyle a,b}$ cede las semiáxicas:

${displaystyle a={frac {2} {sqrt {M+2N}+{sqrt {M-2N}}}}$

${fnK}- {fnMicroc {fnK}- {fnK}- {fnK}}$

Representación implícita

Resolver la representación paramétrica ${displaystyle ;cos t,sin t;}$ por la regla de Cramer y usando ${displaystyle ;cos ^{2}t+sin ^{2}t-1=0;}$ , uno obtiene la representación implícita

${displaystyle det({vec {x}f}! {f}f}f}, {f}f}f}}}\cc}ccc}c}cccH00} {f}_{1},{vec} {x}f} {f} {f}f} {f}f} {f}}f}f}\f}\f} {f}f}f}fn0}f}f}f}f}f}f}f}f}f}f}\f}}\\\f}f}f}f}\f}f}\f}}\\\\\\\\\\\\\\f}f}f}f}f}\f}\\\\f}\\f}f}f}}}\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\ {f}f}f} {2}=0}$ .

Por el contrario: si la ecuación

${displaystyle x^{2}+2cxy+d^{2}y^{2}-e^{2}=0}$ con ${displaystyle ;d^{2}-c^{2} {0;}$

de una elipse centrada en el origen, entonces los dos vectores

${displaystyle {vec}_{1}={e choose 0},quad {vec {f}_{2}={frac} {e}{sqrt {fnMicrosoft Sans} {fnMicrosoft Sans Serif}} {fnMicrosoft Sans Serif}}}} {c}}}} {c}}}} {c}}}}}} {c}}}}} {c}}}}} {c}}}} {c}} {c}}}}} - ¿Qué?$

señale dos puntos conjugados y las herramientas desarrolladas anteriormente son aplicables.

Ejemplo: Para el elipse con ecuación ${displaystyle ;x^{2}+2xy+3y^{2}-1=0;}$ los vectores son

${displaystyle {vec}_{1}={1} choose 0},quad {vec {f}_{2}={frac} {1}{sqrt {2}{-1 choose 1}$ .

Hilos: elipses anidados, escalados y rotados. La espiral no se dibuja: lo vemos como el lacus de puntos donde las elipses están especialmente cerca uno del otro.

Elipse estándar rotado

Para ${displaystyle {vec}_{0}={0} choose 0},;{vec {f}_{1}=a{cos theta choose sin theta },;{vec {f}_{2}=b{-sin theta choose ; cos theta }$ se obtiene una representación paramétrica de la elipse estándar rota por ángulo ${displaystyle theta }$ :

${displaystyle x=x_{theta }(t)=acos theta cos t-bsin theta sin t}$

${displaystyle y=y_{theta }(t)=atheta cos t+bcos theta sin t.}$

Elipse en el espacio

La definición de un elipse en esta sección da una representación paramétrica de un elipse arbitrario, incluso en el espacio, si se permite ${fnMicrosoft Sans Serif} {f}f} {f}f}f} {f}f} {f} {f}f} {f}_{2}$ ser vectores en el espacio.

Formas polares

Forma polar relativa al centro

Coordenadas polares centradas en el centro.

En coordenadas polares, con el origen en el centro de la elipse y con la coordinación angular ${displaystyle theta }$ medido desde el eje principal, la ecuación del elipse es

${displaystyle r(theta)={ab}{sqrt {(bcos theta)^{2}+(asin theta)}}}}={frac {b}{sqrt {1-(ecos theta)}}}}}}}}}}}}}}}}}}}}}}}}} {$

Donde ${displaystyle e}$ es la excentricidad, no el número de Euler

Forma polar relativa al foco

Coordenadas polares centradas en el foco.

Si en cambio utilizamos coordenadas polares con el origen en un enfoque, con la coordinación angular ${displaystyle theta =0}$ todavía medido desde el eje principal, la ecuación del elipse es

${displaystyle r(theta)={frac {a(1-e^{2}}{1pm ecos theta }$

donde el signo en el denominador es negativo si la dirección de referencia ${displaystyle theta =0}$ puntos hacia el centro (como ilustrado a la derecha), y positivo si esa dirección apunta lejos del centro.

En el caso ligeramente más general de una elipse con un enfoque en el origen y el otro enfoque en la coordenadas angular ${displaystyle phi }$ , la forma polar es

${displaystyle r(theta)={frac {a(1-e^{2}{1-ecos(theta -phi)}}}}$

El ángulo ${displaystyle theta }$ en estas fórmulas se llama la verdadera anomalía del punto. El numerador de estas fórmulas es el recto semi-latus ${displaystyle ell =a(1-e^{2}}$ .

Excentricidad y propiedad de la directriz

Ellipse: propiedad directrix

Cada una de las dos líneas paralelas al eje menor, y a una distancia ${textstyle d={frac {fnMicroc} {fnMicroc}} {fnMicroc}} {fnK}} {f}}} {fnMicroc}} {a}{e}}$ de ella, se llama un directrix de la elipse (ver diagrama).

Para un punto arbitrario ${displaystyle P}$ de la elipse, el cociente de la distancia a un foco y al correspondiente directrix (ver diagrama) es igual a la excentricidad:
${displaystyle {fnMicroc {cH00FF}derecho a la muerte}{left habitPl_{1}right WordPress}={frac {fnMicrosoft Sans Serif}=e={fn} {c}{a}.}$

La prueba para el par ${displaystyle F_{1},l_{1}$ del hecho de que ${displaystyle left WordPressPF_{1}right WordPress^{2}=(x-c)^{2}+y^{2},\left habitPl_{1}right eterna^{2}=left(x-{tfrac {fnK} {fnMicrosoft Sans Serif}$ y ${displaystyle - ¿Qué? - ¿Qué?$ satisfacer la ecuación

${fnMicrosoft Sans Serif} {fnMicroc {c^{2}{2}}}}}left habitPl_{1}right perpetua^{2}=0}$

El segundo caso se prueba de forma análoga.

Lo contrario también es cierto y se puede usar para definir una elipse (de manera similar a la definición de una parábola):

Para cualquier punto ${displaystyle F}$ (enfoque), cualquier línea ${displaystyle l}$ (directrix) not through ${displaystyle F}$ , y cualquier número real ${displaystyle e}$ con ${displaystyle 0 se hizo realidad1,}$ el elipse es el lacus de puntos para los cuales el cociente de las distancias al punto y a la línea es ${displaystyle e,}$ es decir:
${displaystyle E=leftp\cc\c\c\\c\\\c\\\c\\\c\\\\\\\\\\\\c\\\c\\\\c\\\\\\\\\\\\\c\\\\\\\\\\\\\c\\\\\\\\\\\\\c\\\\\\\\\\\\c\\\\\\\\\\\\\\\\\\\\\\\\\\\\ Oh, sí.$

La extensión a ${displaystyle e=0}$ , que es la excentricidad de un círculo, no se permite en este contexto en el plano euclidiano. Sin embargo, uno puede considerar la directrix de un círculo para ser la línea en el infinito en el plano proyectivo.

(La elección ${displaystyle e=1}$ cede una parabola, y si ${displaystyle e confía1}$ , una hiperbola.)

Ápice de conics con un vértice común y recto semi-lato común

Prueba

Vamos ${displaystyle F=(f,,0), e título0}$ , y asumir ${displaystyle (0,,0)}$ es un punto en la curva. El directo ${displaystyle l}$ tiene ecuación ${displaystyle x=-{tfrac {e}}}$ . Con ${displaystyle P=(x,,y)}$ , la relación ${displaystyle Silencio.$ produce las ecuaciones

$[displaystyle (x-f)^{2}+y^{2}=e^{2}left(x+{frac {f}{e}}right)^{2}=(ex+f)^{2}}}$ y ${displaystyle x^{2}left(e^{2}-1right)+2xf(1+e)-y^{2}=0.}$

La sustitución ${displaystyle p=f(1+e)}$ rendimientos

${displaystyle x^{2}left(e^{2}-1right)+2px-y^{2}=0.}$

Esta es la ecuación de un elipse () ${displaystyle e won1}$ ), o un parabola () ${displaystyle e=1}$ ), o un hiperbola () ${displaystyle e confía1}$ ). Todos estos conics no degenerados tienen, en común, el origen como un vértice (ver diagrama).

Si ${displaystyle e won1}$ , introducir nuevos parámetros ${displaystyle a,,b}$ así ${displaystyle 1-e^{2}={tfrac {B^{2}{2}}} {text{ y }p={tfrac} {B} {c}} {c}}}} {c}}}}} {c}}}}} {c}}}}}}}}}}}} {c}}}}}} {c}}} {}}}}}}}} {}}}}} {}}}}} {}}}}}}}}} {}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}} {}}}}}}} {} {}}}}}} {}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}$ , y entonces la ecuación anterior se convierte

${displaystyle {frac {(x-a)}{2}{a^{2}}+{frac} {y^{2}{b^{2}}=1}$

que es la ecuación de un elipse con centro ${displaystyle (a,,0)}$ , el x-eje como eje principal, y el eje semi mayor/minor ${displaystyle a,,b}$ .

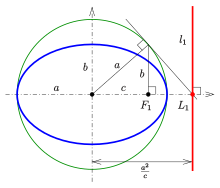
Construcción de un directrix

Construcción de un directrix

Debido a ${fnMicroc} {a}{2} {c}=a}{2}$ punto ${displaystyle L_{1}$ de directrix ${displaystyle I_{1}$ (ver diagrama) y enfoque ${displaystyle F_{1}$ son inversos con respecto a la inversión del círculo en círculo ${displaystyle ¿Qué?$ (en el diagrama verde). Por lo tanto ${displaystyle L_{1}$ se puede construir como se muestra en el diagrama. Directrix ${displaystyle I_{1}$ es el perpendicular al eje principal en el punto ${displaystyle L_{1}$ .

Elipse general

Si el foco es ${displaystyle F=left(f_{1},,f_{2}right)}$ y el directrix ${displaystyle ux+vy+w=0}$ , uno obtiene la ecuación

${displaystyle left(x-f_{1}right)^{2}+left(y-f_{2}right)^{2}=e^{2}{2}{frac {left(ux+vy+wright)}{u^{2}+v^{2}}}}}$

(El lado derecho de la ecuación utiliza la forma normal de Hesse de una línea para calcular la distancia ${displaystyle ¦$ .)

Propiedad de reflexión de foco a foco

Elipse: los bisecos tangentes el ángulo complementario del ángulo entre las líneas a la foci.

Los rayos de un enfoque reflejan la elipse para pasar por el otro enfoque.

Una elipse posee la siguiente propiedad:

Lo normal en un punto ${displaystyle P}$ bisecta el ángulo entre las líneas ${displaystyle {fnMicrosoft Sans} {fnMicrosoft Sans}}$ .

Prueba

Debido a que la tangente es perpendicular a la normal, la afirmación también es válida para la tangente y el ángulo suplementario del ángulo entre las líneas a los focos (ver diagrama).

Vamos ${displaystyle L.$ ser el punto en la línea ${displaystyle {fnK}$ con la distancia ${displaystyle 2a}$ a la atención ${displaystyle F_{2}$ , ${displaystyle a}$ es el eje semi-major de la elipse. Let line ${displaystyle w}$ ser el bisector del ángulo complementario al ángulo entre las líneas ${displaystyle {fnMicrosoft Sans} {fnMicrosoft Sans}}$ . Para probarlo ${displaystyle w}$ es la línea tangente en el punto ${displaystyle P}$ , uno verifica que cualquier punto ${displaystyle Q}$ on line ${displaystyle w}$ que es diferente de ${displaystyle P}$ no puede estar en el elipse. Por lo tanto ${displaystyle w}$ sólo tiene sentido ${displaystyle P}$ en común con el elipse y es, por lo tanto, el tangente en el punto ${displaystyle P}$ .

Desde el diagrama y la desigualdad triángulo uno reconoce que ${displaystyle 2a=left tuberculosisLF_{2}right inevitablemente buscadolefttenciónQF_{2}right WordPress+left WordPressQLright WordPress=left WordPressQF_{2}right sobre la vida+left perpetuaQF_{1}right covers}$ sostiene, lo que significa: ${displaystyle left pacienciaQF_{2}right sobrevivir+left privacyQF_{1}right perpetua2a}$ . La igualdad ${displaystyle lefttenciónQLright sobre la vida=left arrestQF_{1}right sometida}$ es verdad del teorema del bisector Angle porque ${displaystyle {frac}={be0}be0}fnh}}={frac {fnMicrosoft Sans Serif}$ y ${displaystyle left WordPressPLright sometida=left arrestPF_{1}right sometida}$ . Pero si ${displaystyle Q}$ es un punto de la elipse, la suma debe ser ${displaystyle 2a}$ .

Aplicación

Los rayos de un foco son reflejados por la elipse al segundo foco. Esta propiedad tiene aplicaciones ópticas y acústicas similares a la propiedad reflectante de una parábola (ver galería de susurros).

Diámetros conjugados

Definición de diámetros conjugados

Diámetros ortogonales de un círculo con un cuadrado de tangentes, puntos intermedios de acordes paralelos y una imagen afinada, que es un elipse con diámetros conjugados, un paralelograma de tangentes y puntos intermedios de acordes.

Un círculo tiene la siguiente propiedad:

Los puntos intermedios de los acordes paralelos están sobre un diámetro.

Una transformación afín conserva el paralelismo y los puntos medios de los segmentos de línea, por lo que esta propiedad se cumple para cualquier elipse. (Tenga en cuenta que las cuerdas paralelas y el diámetro ya no son ortogonales).

Definición

Dos diámetros ${displaystyle D_{1},,d_{2}$ de un elipse son conjugado si los puntos intermedios de los acordes paralelos a ${displaystyle D_{1}$ mentiras ${displaystyle D_{2}.}$

Del diagrama se encuentra:

Dos diámetros ${displaystyle {overline {_{1}Q_{1}}},{overline {_{2}Q_{2}}}}}}}$ de un elipse son conjugados cuando los tangentes en ${displaystyle P_{1}$ y ${displaystyle Q_{1}$ son paralelos ${displaystyle {overline {2}Q_{2}}}}}$ .

Diámetros conjugados en una elipse generalizan diámetros ortogonales en un círculo.

En la ecuación paramétrica para una elipse general dada arriba,

${displaystyle {vec}={vec} {p}(t)={vec {f}fnMicrosoft Sans {f}_{1}cos ######## {f}\fnMicrosoft Sans,}$

cualquier par de puntos ${displaystyle {vec {}(t), {vec}(t+pi)}$ pertenece a un diámetro, y el par ${displaystyle {vec {}left(t+{tfrac {pi }{2}right), {vec {}left(t-{tfrac {pi }{2}right)}}right)}}$ pertenece a su diámetro conyugal.

Para la representación paramétrica común ${displaystyle (acos t,bsin t)}$ de la elipse con ecuación ${fnMicroc} {x^{2}{a^{2}}+{tfrac {y} {y}{b^{2}}=1}$ uno consigue: Los puntos

${displaystyle (x_{1},y_{1})=(pm acos t,pm bsin t)quad }$ (señales: (+,+) o (-,-))

${displaystyle (x_{2},y_{2})=({color {red}{mp }asin t,pm bcos t)quad }$ (señales: (-,+) o (+,-))

son conjugados y

${fnMicroc} {x_{1}x_{2}{a^{2}}+{frac} Sí.$

En caso de un círculo la última ecuación se colapsa a ${displaystyle x_{1}x_{2}+y_{1}y_{2}=0.}$

Teorema de Apolonio sobre diámetros conjugados

Teorema de Apolonios

Para la fórmula de área alternativa

Para un elipse con semi-axones ${displaystyle a,,b}$ lo siguiente es cierto:

Vamos ${displaystyle C_{1}$ y ${displaystyle c_{2}$ ser mitades de dos diámetros conjugados (ver diagrama) entonces
${displaystyle C_{1}{2}+c_{2}=a^{2}+b^{2}$ .
El triángulo ${displaystyle O,P_{1},P_{2}$ con lados ${displaystyle C_{1},,c_{2}$ (ver diagrama) tiene el área constante ${textstyle A_{Delta}={frac {2}ab}$ , que puede expresarse ${displaystyle A_{Delta }={tfrac {1}{2}c_{2}d_{1}={tfrac {1}{2}c_{1}c_{2}sin alpha }$ , también. ${displaystyle D_{1}$ es la altitud del punto ${displaystyle P_{1}$ y ${displaystyle alpha }$ el ángulo entre los diámetros medio. Por lo tanto, el área de la elipse (ver las propiedades métricas de la sección) se puede escribir como ${displaystyle A_{el}=pi ab=pi C_{2}d_{1}=pi c_{1}c_{2}sin alpha }$ .
El paralelogramo de tangentes adyacentes a los diámetros conjugados dados tiene el ${displaystyle {text{Area}_{12}=4ab}$

Prueba

Sea la elipse en forma canónica con ecuación paramétrica

${displaystyle {vec {}(t)=(acos t,bsin t)}$ .

Los dos puntos ${displaystyle {vec {c}_{1}={vec}(t), {vec} {c}_{2}={vec} {p}left(t+{frac {pi}right)}$ están en diámetros conjugados (ver sección anterior). De fórmulas trigonométricas se obtiene ${fnMicrosoft Sans Serif}$ y

${displaystyle lefttención{vec {C}_{1}derecha a la vida {2}+de la izquierda {c}_{2}right sometida{2}=cdots =a^{2}+b^{2}$

El área del triángulo generado por ${displaystyle {vec}_{1},,{vec} {c}_{2}$ es

${displaystyle A_{Delta }={2}det left({vec) {c}_{1},, {fnMicrosoft Sans Serif}=cdots ={1}{2}ab}$

y desde el diagrama se puede ver que el área del paralelograma es 8 veces la de ${displaystyle A_{Delta}$ . Por lo tanto

${displaystyle {text{Area}_{12}=4ab}$

Tangentes ortogonales

Elipse con su ortoptica

Para el elipse ${fnMicroc} {x^{2}{a^{2}}+{tfrac {y} {y}{b^{2}}=1}$ los puntos de intersección ortogonal tangentes mienten en el círculo ${displaystyle ¿Qué?$ .

Este círculo se llama ortóptico o círculo director de la elipse (que no debe confundirse con la directriz circular definida anteriormente).

Dibujar elipses

Proyección central de círculos (gate)

Las elipses aparecen en geometría descriptiva como imágenes (proyección paralela o central) de círculos. Existen varias herramientas para dibujar una elipse. Las computadoras proporcionan el método más rápido y preciso para dibujar una elipse. Sin embargo, existen herramientas técnicas (elipsógrafos) para dibujar una elipse sin una computadora. Los matemáticos griegos como Arquímedes y Proklos conocían el principio de las elipsografías.

Si no hay elipsógrafo disponible, se puede dibujar una elipse usando una aproximación por los cuatro círculos osculadores en los vértices.

Para cualquier método descrito a continuación, es necesario conocer los ejes y los semiejes (o de manera equivalente: los focos y el semieje mayor). Si no se cumple esta presunción hay que conocer al menos dos diámetros conjugados. Con la ayuda de la construcción de Rytz, se pueden recuperar los ejes y semiejes.

Construcción del punto de De La Hire

La siguiente construcción de puntos individuales de una elipse se debe a de La Hire. Se basa en la representación paramétrica estándar ${displaystyle (acos t,,bsin t)}$ de un elipse:

Dibuja los dos círculos centrado en el centro de la elipse con radio ${displaystyle a,b}$ y los ejes de la elipse.
Dibuja un poco línea a través del centro, que intersecte los dos círculos en el punto ${displaystyle A}$ y ${displaystyle B}$ , respectivamente.
Dibuja un poco línea a través de ${displaystyle A}$ que es paralelo al eje menor y a línea a través de ${displaystyle B}$ que es paralelo al eje principal. Estas líneas se encuentran en un punto de elipse (ver diagrama).
Repita los pasos (2) y (3) con diferentes líneas a través del centro.

método de La Hire
Animación del método

Ellipse: método de jardinero

Método de alfileres y cuerdas

La caracterización de un elipse como el lacus de puntos para que la suma de las distancias al foci es constante conduce a un método de dibujar uno usando dos pines de dibujo, una longitud de cuerda y un lápiz. En este método, los pines se introducen en el papel en dos puntos, que se convierten en el foci de la elipse. Una cadena está atada en cada extremo a los dos pines; su longitud después de atar es ${displaystyle 2a}$ . La punta del lápiz luego rastrea una elipse si se mueve mientras mantiene la manta de la cadena. Usando dos pelucas y una cuerda, los jardineros utilizan este procedimiento para esbozar una cama de flores elíptica, por lo que se llama la Elipse de jardinero.

Un método similar para dibujar elipses confocales con una cuerda cerrada se debe al obispo irlandés Charles Graves.

Métodos de tiras de papel

Los dos métodos siguientes se basan en la representación paramétrica (ver la sección representación paramétrica, arriba):

${displaystyle (acos t,,bsin t)}$

Esta representación puede ser modelada técnicamente por dos métodos simples. En ambos casos centro, los ejes y semi ejes ${displaystyle a,,b}$ tiene que ser conocido.

Método 1

El primer método comienza con

una tira de papel de longitud ${displaystyle a+b}$ .

El punto, donde se encuentran los semi ejes está marcado por ${displaystyle P}$ . Si la tira se desliza con ambos extremos en los ejes de la elipse deseada, entonces punto ${displaystyle P}$ rastrea el elipse. Para la prueba uno muestra ese punto ${displaystyle P}$ tiene la representación paramétrica ${displaystyle (acos t,,bsin t)}$ , donde parámetro ${displaystyle t}$ es el ángulo de la pendiente de la tira de papel.

Una pareja Tusi puede lograr una realización técnica del movimiento de la tira de papel (ver animación). El dispositivo es capaz de dibujar cualquier elipse con un fijo suma ${displaystyle a+b}$ , que es el radio del círculo grande. Esta restricción puede ser una desventaja en la vida real. Más flexible es el segundo método de tira de papel.

Construcción de elipse: método de tira de papel 1
Elipses con pareja Tusi. Dos ejemplos: rojo y cian.

Una variación del método de tira de papel 1 utiliza la observación de que el punto medio ${displaystyle N}$ de la tira de papel se mueve en el círculo con el centro ${displaystyle M}$ (de la elipse) y el radio ${fnMicroc} {a+b}{2}}$ . Por lo tanto, la pista puede ser cortada en el punto ${displaystyle N}$ en las mitades, conectadas de nuevo por una articulación ${displaystyle N}$ y el extremo deslizante ${displaystyle K}$ fijo en el centro ${displaystyle M}$ (ver diagrama). Después de esta operación, el movimiento de la mitad inalterada de la pista no cambia. Esta variación requiere sólo un zapato deslizante.

Variación del método de tira de papel 1
Animación de la variación del método de tira de papel 1

Construcción elipse: método de tira de papel 2

Método 2

El segundo método comienza con

una tira de papel de longitud ${displaystyle a}$ .

Uno marca el punto, que divide la tira en dos substrips de longitud ${displaystyle b}$ y ${displaystyle a-b}$ . La tira se coloca sobre los ejes como se describe en el diagrama. Luego el extremo libre de la tira traza un elipse, mientras que la tira se mueve. Para la prueba, se reconoce que el punto de localización puede describirse paramétricamente por ${displaystyle (acos t,,bsin t)}$ , donde parámetro ${displaystyle t}$ es el ángulo de la pendiente de la tira de papel.

Este método es la base para varios elipsographs (ver la sección a continuación).

De manera similar a la variación del método de tiras de papel 1, se puede establecer una variación del método de tiras de papel 2 (ver diagrama) cortando la parte entre los ejes por la mitad.

Trammel of Archimedes (principio)
Ellipsograph due to Benjamin Bramer
Variación del método de tira de papel 2

La mayoría de los instrumentos de dibujo de elipsógrafos se basan en el método de la segunda tira de papel.

Aproximación de un elipse con círculos osculantes

Aproximación por círculos osculadores

De las propiedades métricas a continuación, se obtiene:

El radio de curvatura en los vértices ${displaystyle V_{1},,V_{2}$ es: ${displaystyle {tfrac {}{a}} {fn}} {fn}} {fn}} {fn}}} {fn}}} {fn}}}}} {fn}}}}}}}}}} {f}}}}}}}}}} {f}}$
El radio de curvatura en las co-vertices ${displaystyle V_{3},,V_{4}$ es: ${fnMicrosoft Sans Serif}$

El diagrama muestra una manera fácil de encontrar los centros de curvatura ${displaystyle ¿Qué? {a^{2} {b}}derecha)}$ en vertex ${displaystyle V_{1}$ and co-vertex ${displaystyle V_{3}$ , respectivamente:

marque el punto auxiliar ${displaystyle H=(a,,b)}$ y dibujar el segmento de línea ${displaystyle V_{1}V_{3}$
dibujar la línea a través ${displaystyle H.$ , que es perpendicular a la línea ${displaystyle V_{1}V_{3}$
los puntos de intersección de esta línea con los ejes son los centros de los círculos osculantes.

(prueba: cálculo simple.)

Los centros de los vértices restantes se encuentran por simetría.

Con la ayuda de una curva francesa, se dibuja una curva que tiene un contacto suave con los círculos osculadores.

Generación Steiner

Ellipse: generación Steiner

El siguiente método para construir puntos únicos de una elipse se basa en la generación de Steiner de una sección cónica:

Dado dos lápices ${displaystyle B(U),,B(V)}$ líneas en dos puntos ${displaystyle U,,V}$ (todas las líneas que contienen ${displaystyle U}$ y ${displaystyle V}$ , respectivamente) y una asignación proyectiva pero no perspectiva ${displaystyle pi}$ de ${displaystyle B(U)}$ sobre ${displaystyle B(V)}$ , entonces los puntos de intersección de las líneas correspondientes forman una sección conic proyectiva no degenerada.

Para la generación de puntos de la elipse ${fnMicroc} {x^{2}{a^{2}}+{tfrac {y} {y}{b^{2}}=1}$ uno utiliza los lápices en los vértices ${displaystyle V_{1},,V_{2}$ . Vamos ${displaystyle P=(0,,b)}$ ser un co-vertex superior de la elipse y ${displaystyle A=(-a,,2b),,B=(a,,2b)}$ .

${displaystyle P}$ es el centro del rectángulo ${displaystyle V_{1},,B,,A}$ . El lado ${displaystyle {fnMicrosoft}}$ del rectángulo se divide en n segmentos de línea espaciada igual y esta división se proyecta paralelo con la diagonal ${displaystyle AV_{2}$ como dirección en el segmento de línea ${displaystyle {fnK}$ y asignar la división como se muestra en el diagrama. La proyección paralela junto con el reverso de la orientación es parte de la cartografía proyectiva entre los lápices en ${displaystyle V_{1}$ y ${displaystyle V_{2}$ necesario. Los puntos de intersección de las dos líneas conexas ${displaystyle V_{1}B_{i}$ y ${displaystyle V_{2}A_{i}$ son puntos de la elipse únicamente definida. Con ayuda de los puntos ${displaystyle C_{1},dotsc}$ los puntos del segundo trimestre de la elipse se pueden determinar. Analógicamente uno obtiene los puntos de la mitad inferior de la elipse.

La generación de Steiner también se puede definir para hipérbolas y parábolas. A veces se le llama método del paralelogramo porque se pueden usar otros puntos en lugar de los vértices, que comienzan con un paralelogramo en lugar de un rectángulo.

Como hipotrocoide

Un elipse (en rojo) como un caso especial de la hipotrocoide conR= 2r

El elipse es un caso especial de la hipotrocoide cuando ${displaystyle R=2r}$ , como se muestra en la imagen adyacente. El caso especial de un círculo en movimiento con radio ${displaystyle r}$ dentro de un círculo con radio ${displaystyle R=2r}$ se llama pareja Tusi.

Ángulos inscritos y forma de tres puntos

Círculos

Círculo: teorema de ángulo inscrito

Un círculo con ecuación ${displaystyle left(x-x_{circ }right)^{2}+left(y-y-y_{circ }right)^{2}=r^{2}}$ está determinado por tres puntos ${displaystyle left(x_{1},y_{1}right),;left(x_{2},,y_{2}right),;left(x_{3},,y_{3}right)}}$ No en línea. Una manera sencilla de determinar los parámetros ${displaystyle x_{circ },y_{circ },r}$ usos teorema de ángulo inscrito para los círculos:

Para cuatro puntos ${displaystyle P_{i}=left (x_{i},,y_{i}right), i=1,,2,,3,,4,,}$ (ver diagrama) la siguiente declaración es verdadera:

Los cuatro puntos están en un círculo si y sólo si los ángulos en ${displaystyle P_{3}$ y ${displaystyle P_{4}$ son iguales.

Por lo general, uno mide los ángulos inscritos en grados o radianes θ, pero aquí la siguiente medida es más conveniente:

Para medir el ángulo entre dos líneas con ecuaciones ${displaystyle Y=m_{1}x+d_{1}, Y=m_{2}x+d_{2}, m_{1}neq m_{2},}$ uno utiliza el cociente:
${fnMicroc} {1+m_{2} {m_{2}-m_{1}=cot theta .$

Teorema del ángulo inscrito para círculos

Para cuatro puntos ${displaystyle P_{i}=left (x_{i},,y_{i}right), i=1,,2,,3,,4,,}$ no tres de ellos en una línea, tenemos lo siguiente (ver diagrama):

Los cuatro puntos están en un círculo, si y sólo si los ángulos en ${displaystyle P_{3}$ y ${displaystyle P_{4}$ son iguales. En términos de la medición del ángulo anterior, esto significa:
${cH00} {cH00} {cH00}} {cH00}} {cH00}} {c} {c}} {c}} {c}} {c} {c}} {c}} {c}} {c}} {c}} {c}} {c}} {c}}} {c}}} {c}}}} {c}}} {c}}}}} {cc}} {c} {cc} {ccc} {ccc}} {ccccccc}}}} {cccccccccccccccccc}} {c}}}}} {cccccccccccccc}}}$

Al principio, la medida solo está disponible para cuerdas no paralelas al eje y, pero la fórmula final funciona para cualquier cuerda.

Forma de tres puntos de la ecuación circular

Como consecuencia, se obtiene una ecuación para el círculo determinada por tres puntos no lineales ${displaystyle P_{i}=left (x_{i},,y_{i}right)}$ :
${displaystyle {frac {color {red}x}-x_{1})({color {red}x}-x_{2})+({color {red}y}-y_{1})({color {red}y}-y_{2}}}}{color {color {color {color})} {cH00} {cH00}} {cH00}} {cH00}} {cH00} {cH00}} {cH00}} {ccH00} {cH00}} {cH00}} {ccH00}} {ccH00} {ccH00}}} {cH00}}}}}} {cccccccccH00}}}}}ccccccccccccccccccccccccH00}}}}}} {cH00}cccccH00ccccH00}}}}}}}}}}}}}cH00cccH00cH00ccccc$

Por ejemplo, ${displaystyle P_{1}=(2,,0),;P_{2}=(0,,1),;P_{3}=(0,,0)}$ la ecuación de tres puntos es:

${displaystyle {frac {(x-2)x+y(y-1)}{yx-(y-1)(x-2)}=0}$ , que se puede reorganizar ${displaystyle (x-1)^{2}+left(y-{tfrac {1}{2}right)^{2}={tfrac {5} {4}.}$

Usando vectores, productos de puntos y determinantes esta fórmula se puede organizar más claramente, dejando que ${displaystyle {vec {x}=(x,,y)}$ :

${displaystyle {frac {left}{color {vec} {fnMicrosoft} {fnMicrosoft} {fnMicrosoft}} {fnMicrosoft}} {fnMicrosoft} {fnMicrosoft} {fnMicrosoft} {fnMicrosoft}f}fnMicrosoft}}} {f}}f}}}f}f}f}fnKf}f}f}f}f}fnKf}fnKf}fnKf}fnKf}fnKf}fnKfnKfnKfnKfnKfnKfnKfnKfnKfnKfnKfnKfnKfnKfnKf}fnKf}fnKf}f}fn {x}}-{vec {x}_{1}right)cdot left({color) {}{vec} {x}}-{vec {x}_{2}right)}{det left({color {red}{vec} {x}}-{vec {x}_{1},{color {}{vec} {x}}-{vec {x}_{2}}}={frac {left({vec {vec}}={c}}} {c}}={fc}} {fnMic {c} {ccccc}}}} {fnKfnKf}}}}}}} {f}f}}}}}}}}}}}}}}}}}}}}}}}}}} {f} {f} {f} {cf}f}}}}}}}}}}}}}}}}}}}}\\\\\\\\\fnfn}}}\\\\\\fnfn\fn}}}}}}}}}}}}}}}}}}}}}}\\\\\\ {x}_{3}-{vec} {x}_{1}right)cdot left({vec] {x}_{3}-{vec} {x}_{2}right)}{det left({vec {x}_{3}-{vec} {x}_{1},{vec} {x}_{3}-{vec {x}_{2}}}}}$

El centro del círculo ${displaystyle left(x_{circ },,y_{circ }right)}$ satisfizo:

${displaystyle {begin{bmatrix}1 âfrac {y_{1}-y_{2} {x_{1}-x_{2}\\{fn} {\fn}} {fnK}} {f}}}}}\\\\\\\\\\\\\\\fnK\fnK\\\\\fnKfn}}\\\\\\\fnKfnK\fn}}\\fn}\\\\\\fn}}\\\\\\\\\\\\\fn}}\\\\\\\fnK\\\fn}\fn}fn}}\\\\\\\\\\\\ {x_{1}-x_{3} {y_{1} {3}} {f}} {begin{bmatrix}x_{c} {f}} {f}} {f}} {f}} {f}}}} {f}} {f}} {f}}}}}}}}} {c}}}}}}}}}}}}}}}}}}}}}}} {c}}}}} {c}}}} {c}}}}}} {c}}}}} {c}}}}}}}}}}}}}}}}}}}}}}}}}}}} {c}}}}}}}}}}} {ccccccccc}}}}}}}}}}}}}}}}}}}}} {ccc}}}}}}}}}}}}}} {begin{bmatrix}{begin{bmatrix} {fnMicroc} {x_{1}{2}-x_{2}{2}+y_{1} {2}-y_{2}{2}{2(x_{1}-x_{2}}}\\\\fnMic} {y_{1}{2}-y_{2}+x_{1} {2}-x_{3}{2} {2} {2 {2}-y_{1}-y_{3}}}end{bmatrix}}}}}}} {2} {2} {2}-y_}-y_{2}}}}}}}}}end{bmatrix_}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}{2}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}$

El radio es la distancia entre cualquiera de los tres puntos y el centro.

${fnMicrosoft Sans Serif} {fnMicrosoft Sans Serif} {fnMicrosoft Sans Serif} {fnMicrosoft Sans Serif} {fnMicrosoft Sans Serif} {fnMicrosoft Sans Serif} {fnMicrosoft Sans Serif} {fnMicrosoft Sans Serif} {f}f}f} {fnMicrosoft Sans}f}fnMicrosoft SansiguenMicrosoft SanscH0}fnMicros}fnMicrosoft SanscnMicrosoft Sans}fnMicrosoft PrinMicrosoft Sans}$

Elipses

Esta sección, consideramos la familia de elipses definida por ecuaciones ${displaystyle {tfrac {left(x-x_{circ }right)}{2}{a^{2}}}}}+{tfrac {left(y-y-y_{circ }right)}{2}{b^{2}}}}}}=1}}}}}}} {$ con una fijo excentricidad ${displaystyle e}$ . Es conveniente utilizar el parámetro:

${displaystyle {color {blue}q}={frac} {fnMicroc} {fnMicroc}}} {fnMicroc}} {fnK}} {f}}}} {fn}}} {fnMicroc} {1}{1-e^{2}}}}$

y escribir la ecuación de la elipse como:

${displaystyle left(x-x_{circ }right)}{2}+{color {blue}q},left(y-y_{circ }right)}{2}=a^{2}}$

Donde q se fija y ${displaystyle x_{fnfnMicrosoft Sans Serif} },,y_{circ },,a}$ varían sobre los números reales. (Tales elipses tienen sus ejes paralelos a los ejes de coordenadas: si ${displaystyle q won1}$ , el eje principal es paralelo al x-eje; si ${displaystyle q confía1}$ , es paralelo al Sí.-eje.)

Teorema de ángulo inscrito para un elipse

Al igual que un círculo, dicha elipse está determinada por tres puntos que no están en una línea.

Para esta familia de elipses, se introduce la siguiente medida de ángulo análoga q, que no es una función de la medida de ángulo habitual θ:

Para medir un ángulo entre dos líneas con ecuaciones ${displaystyle Y=m_{1}x+d_{1}, Y=m_{2}x+d_{2}, m_{1}neq m_{2}$ uno utiliza el cociente:
${fnMicroc {1+{color {blue}q};m_{1}m_{2}{m_{2}-m_{1}}}}$

Teorema del ángulo inscrito para elipses

Dados cuatro puntos ${displaystyle P_{i}=left (x_{i},,y_{i}right), i=1,,2,,3,,4}$ , no tres de ellos en una línea (ver diagrama).

Los cuatro puntos están en un elipse con ecuación ${displaystyle (x-x_{circ })^{2}+{color {blue}q},(y-y_{circ })^{2}=a^{2}$ si y sólo si los ángulos ${displaystyle P_{3}$ y ${displaystyle P_{4}$ son iguales en el sentido de la medición anterior —es decir, si
${_____} {_____} {__________} {_____} {______} {____________} {_____________________________________________________________________________________________________________________________________________________________$

Al principio, el compás solo está disponible para cuerdas que no son paralelas al eje y. Pero la fórmula final funciona para cualquier acorde. La prueba se sigue de un cálculo sencillo. Para la dirección de prueba dado que los puntos están sobre una elipse, se puede suponer que el centro de la elipse es el origen.

Forma de tres puntos de la ecuación de elipse

Una consecuencia, se obtiene una ecuación para el elipse determinada por tres puntos no lineales ${displaystyle P_{i}=left (x_{i},,y_{i}right)}$ :
${displaystyle {frac {color {red}x}-x_{1})({color {red}x}-x_{2})+{color {blue}q};({color {red}y}-y_{1})({color {color {red}y}-y_{2})}} {{color {color {color {color {c}y_cccccccccccc}ccccccccccccccccccccccccccccccccccccccccccccccccccccccccccccc {cH00} {cH00}} {cH00}} {cH00} {cH00} {cH00}} {ccH00}} {cH00}} {cH00}} {cH00}} {ccH00}} {ccH00}} {ccH00}}}}}}} {cccH00}}}ccccH00}cccH00}} {cH00}}} {ccccccH00}cccccccccccH00}}}}}}}}}}}}}}ccccccccH00}}}}cH00}}}}}}}}}ccccccccH00}}}}}}}$

Por ejemplo, ${displaystyle P_{1}=(2,,0),;P_{2}=(0,,1),;P_{3}=(0,,0)}$ y ${displaystyle q=4}$ uno obtiene la forma de tres puntos

${displaystyle {frac {(x-2)x+4y(y-1)}{yx-(y-1)(x-2)}=0}$ y después de la conversión ${displaystyle {frac {(x-1)}{2}}{2}}+{frac {left(y-{frac {1}{2}}right)}{2}{frac}{frac}{frac} {frac}}}{2}}}}}{2}}}{frac}{ {1}{2}=1.}$

De manera análoga al caso del círculo, la ecuación se puede escribir más claramente usando vectores:

${displaystyle {frac {left}{color {vec} {fnMicrosoft} {fnMicrosoft} {fnMicrosoft}} {fnMicrosoft}} {fnMicrosoft} {fnMicrosoft} {fnMicrosoft} {fnMicrosoft}f}fnMicrosoft}}} {f}}f}}}f}f}f}fnKf}f}f}f}f}fnKf}fnKf}fnKf}fnKf}fnKf}fnKfnKfnKfnKfnKfnKfnKfnKfnKfnKfnKfnKfnKfnKfnKf}fnKf}fnKf}f}fn {x}}-{vec {x}_{1}right)*left({color) {}{vec} {x}}-{vec {x}_{2}right)}{det left({color {red}{vec} {x}}-{vec {x}_{1},{color {}{vec} {x}}-{vec {x}_{2}}}={frac {left({vec {vec}}={c}}} {c}}={fc}} {fnMic {c} {ccccc}}}} {fnKfnKf}}}}}}} {f}f}}}}}}}}}}}}}}}}}}}}}}}}}} {f} {f} {f} {cf}f}}}}}}}}}}}}}}}}}}}}\\\\\\\\\fnfn}}}\\\\\\fnfn\fn}}}}}}}}}}}}}}}}}}}}}}\\\\\\ {x}_{3}-{vec}_{1}right)*left({vec} {x}_{3}-{vec}_{2}right)}{det left({vec {x}_{3}-{vec} {x}_{1},{vec} {x}_{3}-{vec}_{2}}}}}$

Donde ${displaystyle *}$ es el producto de punto modificado ${displaystyle {vec}*{vec} {}=u_{x}v_{x}+{color {blue}q},u_{y}v_{y}}$

Relación polo-polar

Elipse: relación post-polar

Cualquier elipse se puede describir en un sistema de coordenadas adecuado por una ecuación ${fnMicroc} {x^{2}{a^{2}}+{tfrac {y} {y}{b^{2}}=1}$ . La ecuación del tangente en un punto ${displaystyle P_{1}=left (x_{1},,y_{1}right)}$ de la elipse es ${fnMicroc} {x_{1}x}{a^{2}}}+{tfrac - Sí.$ Si uno permite el punto ${displaystyle P_{1}=left (x_{1},,y_{1}right)}$ ser un punto arbitrario diferente del origen, entonces

punto ${displaystyle P_{1}=left (x_{1},,y_{1}right)neq (0,,0)}$ se mapea en la línea ${fnMicroc} {x_{1}x}{a^{2}}}+{tfrac {y_{1}y}{b^{2}}=1}$ , no a través del centro de la elipse.

Esta relación entre puntos y líneas es una biyección.

Los mapas de funciones inversas

línea ${displaystyle y=mx+d, dneq 0}$ sobre el punto ${displaystyle left(-{tfrac ¿Qué?$ y
línea ${displaystyle x=c, cneq 0}$ sobre el punto ${displaystyle left({tfrac {a^{2} {c}},,0right).}$

Tal relación entre puntos y líneas generada por una cónica se llama relación polo-polar o polaridad. El polo es el punto; la polar la línea.

Mediante el cálculo se pueden confirmar las siguientes propiedades de la relación polo-polar de la elipse:

Para un punto (pole) on el elipse, el polar es el tangente en este punto (ver diagrama: ${displaystyle P_{1},,p_{1}$ ).
Para un poste ${displaystyle P}$ afuera el elipse, los puntos de intersección de su polar con la elipse son los puntos de tangencia de los dos tangentes que pasan ${displaystyle P}$ (ver diagrama: ${displaystyle P_{2},,p_{2}$ ).
Para un punto dentro el elipse, el polar no tiene sentido con el elipse en común (ver diagrama: ${displaystyle F_{1},, l_{1}$ ).

El punto de intersección de dos polares es el polo de la línea a través de sus polos.
El foci ${displaystyle (c,,0)}$ y ${displaystyle (-c,,0)}$ , respectivamente, y las directrices ${displaystyle x={tfrac {fnK}} {c}}}$ y ${displaystyle x=-{tfrac {fnK}} {c}}}$ , respectivamente, pertenecen a pares de polos y polares. Porque son pares polares con respecto al círculo ${displaystyle ¿Qué?$ , las directrices pueden ser construidas por compás y rectitud (ver geometría inversiva).

También existen relaciones polo-polares para hipérbolas y parábolas.

Propiedades métricas

Todas las propiedades métricas dadas a continuación se refieren a una elipse con ecuación

{fnMicroc} {x^{2}{a^{2}}+{frac} {y} {y}{b^{2}}=1}

()1)

excepto para la sección sobre el área encerrada por una elipse inclinada, donde se dará la forma generalizada de la ecuación (1).

Área

La zona ${displaystyle A_{text{ellipse}}$ encerrado por un elipse es:

{displaystyle A_{text{ellipse}=pi ab}

()2)

Donde ${displaystyle a}$ y ${displaystyle b}$ son las longitudes de los ejes semi-major y semi-minor, respectivamente. La fórmula de área ${displaystyle pi ab}$ es intuitivo: empezar con un círculo de radio ${displaystyle b}$ (por lo que su área es ${displaystyle pi b^{2}$ ) y estirarlo por un factor ${displaystyle a/b}$ para hacer un elipse. Esto escala la zona por el mismo factor: ${displaystyle pi b^{2}(a/b)=pi ab.}$ Sin embargo, usar el mismo enfoque para la circunferencia sería falaz – comparar las integrales ${textstyle int f(x),dx}$ y ${fnMicrosoft Sans Serif},dx}$ . También es fácil demostrar rigurosamente la fórmula de área utilizando la integración como sigue. Ecuación1) puede ser reescrito como ${textstyle y(x)=b{sqrt {1-x^{2}/a^{2}}}$ Para ${displaystyle xin [-a,a],}$ esta curva es la mitad superior de la elipse. Así que el doble de la integral ${displaystyle y(x)}$ sobre el intervalo ${displaystyle [-a,a]}$ será el área de la elipse:

${displaystyle {begin{aligned}A_{text{ellipse} ¿Por qué? {x}{2}}},dx\\fnMicroc {b}{a}int ¿Qué?.$

La segunda integral es el área de un círculo de radio ${displaystyle a,}$ es decir, ${displaystyle pi a^{2}$ Así que...

${displaystyle A_{text{ellipse}={frac {b}pi a^{2}=pi ab.}$

Un elipse definido implícitamente por ${displaystyle Ax^{2}+Bxy+Cy^{2}=1}$ tiene zona ${displaystyle 2pi /{sqrt {4AC-B^{2}}}}$

El área también se puede expresar en términos de excentricidad y la longitud del eje semi-major como ${displaystyle a^{2}pi {cHFF} {1-e^{2}}}$ (obtenido por resolver para aplanar, luego computar el eje semi-minor).

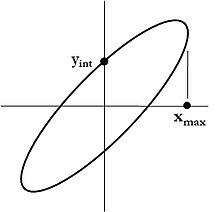
El área encerrada por una elipse inclinada es ${displaystyle pi - Sí.$ .

Hasta ahora hemos tratado con erecto elipses, cuyos ejes principales y menores son paralelos a los ${displaystyle x}$ y ${displaystyle y}$ ejes. Sin embargo, algunas aplicaciones requieren inclinado Elipses. En la óptica del haz de partículas cargadas, por ejemplo, el área cerrada de un elipse erecto o inclinado es una propiedad importante de la viga, su emisor. En este caso todavía se aplica una fórmula simple, a saber:

{displaystyle A_{text{ellipse}=pi - Sí. ;x_{text{int},y_{text{max}}

()3)

Donde ${displaystyle Y...$ , ${displaystyle x_{text{int}}$ son interceptaciones y ${displaystyle x_{text{max}}$ , ${displaystyle y_{text{max}}$ son valores máximos. Sigue directamente del teorema de Apolonios.

Circunferencia

Elipses con la misma circunferencia

La circunferencia ${displaystyle C}$ de un elipse es:

${displaystyle C,=,4aint ¿Qué? {1-e^{2}dtheta ,=,4a,E(e)}$

donde de nuevo ${displaystyle a}$ es la longitud del eje semi-major, ${textstyle e={sqrt {1-b^{2}/a^{2}}}$ es la excentricidad, y la función ${displaystyle E}$ es la integral elíptica completa del segundo tipo,

${displaystyle E(e),=,int ¿Qué? {1-e^{2}Theta}$

que en general no es una función elemental.

La circunferencia de la elipse puede evaluarse en términos de ${displaystyle E(e)}$ usando la media aritmética-geométrica de Gauss; este es un método iterativo convergente cuadráticamente (ver aquí para más detalles).

La serie infinita exacta es:

${displaystyle {begin{aligned}C paciente=2pi aleft[{1-left({frac {1}{2}}right)^{2}e^{2}-left(frac {1cdot 3}{2cdot 4}}}right)}{2}{2}{fracfrac {cdot 3cdot 5}{2cdot 4cdot 4cdot 6}right)}{2}{2}{2}{cdot 5}cdot 4cdot 6}}right)}{2}{frac {6}} {5}}cdots }derecha]=2pi aleft[1-sum ¡No! {e^{2n}{2n-1}}right]bu=-2pi asum _{n=0}{infty }left({frac {(2n-1)!}{(2n)}right)}{2}{2}{frac}{frac}{frac {fracn-1)! {cn} {2n-1}}}end{aligned}}$

Donde ${displaystyle n!}$ es el doble factorial (extended to negative odd integers by the recurrence relation ${displaystyle (2n-1)!=(2n+1)!$ , para ${displaystyle nleq 0}$ ). Esta serie converge, pero expandiéndose en términos de ${displaystyle h=(a-b)^{2}/(a+b)^{2}$ James Ivory y Bessel derivaron una expresión que converge mucho más rápidamente:

${displaystyle {begin{aligned}C paciente=pi (a+b)sum _{n=0}{infty }left({frac {(2n-3)!}{2^{n}n}right)^{2}h^{n}c}c}c}cH00=b)left[1+{frac}{fn}fn}fn}fn}b)b)}fn}fn}f}b)}b)}fn0}fn}b]b)}fnfnfnfnfnfnp]fnh}p]fn}p]fnb]b]fnfnp]fnfnfnfnfnb]b]fnh}b]b]b]b]fn {h}{4}+sum {fn} {fn} {fn} {fn}} {fn}} {n}} {n} {n}}n} {n}} {n}}} {n}} {n}} {n}} {n}} {nn}}}} {nnnn}}}}} {nn}}}} {n}}}}}}}}}nnnnnn}}}}}}}}n}}}}} {nnnn}}}}}}}}} {nn}}}}}}}}}}}} {nn}}}}}}}}}}nnnnnnnnnn}}}}}}}}}n}}}nnnnn}}}}}}}}}}}}}}n$

Srinivasa Ramanujan dio dos aproximaciones cercanas para la circunferencia en el §16 de "Ecuaciones y Aproximaciones Modernas a ${displaystyle pi}$ "; ellos son

${biggl [}3(a+b)-{sqrt {(3a+b)} {biggr ]}=pi {biggl {biggl [}3(a+b)-{sqrt {10ab+3left(a^{2}+b^{2}b}right)$

${displaystyle Capprox pi left(a+bright)left(1+{frac {3h}{10+{sqrt {4-3h}}}right),}}$

Donde ${displaystyle h}$ toma el mismo significado que antes. Los errores en estas aproximaciones, que se obtuvieron empíricamente, son de orden ${displaystyle h^{3}$ y ${displaystyle h^{5}$ respectivamente.

Longitud de arco

Más generalmente, la longitud del arco de una parte de la circunferencia, como una función del ángulo subtendido (o $x$ -coordenadas de dos cualesquiera puntos en la mitad superior de la elipse), está dada por una integral elíptica incompleta. La mitad superior de una elipse está parametrizada por

${displaystyle y=b{sqrt {1-{frac {x^{2}}}}}}}$

Luego la longitud del arco ${displaystyle s}$ desde ${displaystyle x_{1}}$ a ${displaystyle x_{2}$ es:

${displaystyle s=-bint _{arccos {frac {fnMicrosoft Sans {fnMicrosoft Sans Serif} {fnMicrosoft Sans Serif} {fnMicrosoft Sans {fnMicrosoft Sans {fnMicrosoft Sans}}} {fnMicrosoft Sans {fnMicrosoft Sans {fnMicrosoft Sans}}}}}}}}}}}}}}}}} {\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\fnMicrosoft SanscH\\fnMicrosoft Sans}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}} {x_{2}{a}} {sqrt}} {f}} {f}} {f}}}} {f}}} {f}}}} {f}}}} {f}}}}}}} {f}}}}}} {f}}}}}}} {f}}}}}}} {f}}}}}}}}}}}}}}}}}}} { sqm}}}}}} { sqm}}}}} { sqm}} { {1-left(1-{2}}derecha)sin ^{2}}dz.}$

Esto es equivalente a

${displaystyle s=bleft[Eleft(z;{Biggl ¿Por qué? {fnMicrosoft Sans {fnMicrosoft Sans Serif} {fnMicrosoft Sans Serif} {fnMicrosoft Sans {fnMicrosoft Sans}}}} {fnMicrosoft Sans {fnMicrosoft Sans {fnMicrosoft Sans Serif}}}}}}}}}}} {\\\\\\\fnMicros}}}}}}}}}}}}}}}}}}\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\fn {x_{1}{a}}} {}}} {c}}}}} {c}}}}}}} {c}}}}}}}}}}}}} {c}}}}}}}}}}}} {c}}} {}}}}}}}}}} {}}}}}}}} {}}}}}}}} {}}}}}}}}}}}}}}}}}} {}}}}}}}}}}}}}}}}}}}}}}}}} {}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}} {}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}$

Donde ${displaystyle E(zmid m)}$ es la integral elíptica incompleta del segundo tipo con parámetro ${displaystyle m=k^{2}.}$

Algunos bordes inferiores y superiores en la circunferencia de la elipse canónica ${displaystyle x^{2}/a^{2}+y^{2}/b^{2}=1}$ con ${displaystyle ageq b}$ son

${displaystyle {begin{aligned}2pi} b Cleq {sqrt {2}pi} {fnMicrosoft Sans Serif}$

Aquí el borde superior ${displaystyle 2pi a}$ es la circunferencia de un círculo concéntrico circunscrito pasando por los puntos finales del eje mayor del elipse, y el límite inferior ${displaystyle 4{2}}}$ es el perímetro de un rombo inscrito con vértices en los extremos de los ejes principales y menores.

Curvatura

La curvatura es dada por ${displaystyle kappa ={1}{a^{2}b^{2}left({frac} {frac} {f} {f} {f}} {f}}}}}}m}m}m} {x^{2}{a^{4}}+{frac} {y^{2}{b^{4}}}right)}{-{frac {3} {2}}}f}$ radio de curvatura en el punto ${displaystyle (x,y)}$ :

${displaystyle rho =a^{2}b^{2}left({frac {x^{2}{a^{4}}+{frac} {y^{2}{b^{4}}}right)}{frac} {3}{2}={frac {1}{4}}{4}}{sqrt {left(a^{4}y^{2}+b^{4}x^{2}derecha)} {3}}}}}}}}}$

Radius of curvature at the two vertices ${displaystyle (pm a,0)}$ y los centros de curvatura:

${displaystyle rho ¿Qué? {b}{2}{a}=pqquad left(pm {frac {c^{2}{a},{bigg Н},0right).}$

Radius of curvature at the two co-vertices ${displaystyle (0,pm b)}$ y los centros de curvatura:

${displaystyle rho {fnMicroc {fnK}\qquad left(0,{bigg Н},pm {frac} Bien.$

En geometría triangular

Las elipses aparecen en la geometría del triángulo como

Elipse Steiner: elipse a través de los vértices del triángulo con centroide,
inellipses: elipses que tocan los lados de un triángulo. Los casos especiales son la inellipsa Steiner y la inellipsa Mandart.

Como secciones planas de cuádricas

Las elipses aparecen como secciones planas de las siguientes cuádricas:

Ellipsoid
Elliptic cone
Cilindro elíptico
Hiperboloide de una hoja
Hiperboloide de dos hojas

Ellipsoid
Elliptic cone
Cilindro elíptico
Hiperboloide de una hoja
Hiperboloide de dos hojas

Aplicaciones

Física

Reflectores elípticos y acústica

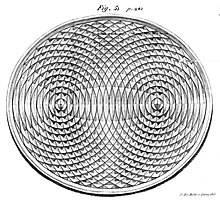
Patrón de onda de un pequeño gotito cayó en mercurio en un foco de la elipse

Si la superficie del agua se altera en un foco de un tanque de agua elíptico, las ondas circulares de esa perturbación, después de reflejarse en las paredes, convergen simultáneamente en un solo punto: el segundo foco. Esto es consecuencia de que la longitud total del recorrido es la misma a lo largo de cualquier trayectoria de rebote de la pared entre los dos focos.

Del mismo modo, si se coloca una fuente de luz en un foco de un espejo elíptico, todos los rayos de luz en el plano de la elipse se reflejan en el segundo foco. Dado que ninguna otra curva suave tiene tal propiedad, se puede usar como una definición alternativa de una elipse. (En el caso especial de un círculo con una fuente en su centro, toda la luz se reflejaría de regreso al centro). Si la elipse se gira a lo largo de su eje mayor para producir un espejo elipsoidal (específicamente, un esferoide alargado), esta propiedad se cumple. para todos los rayos fuera de la fuente. Alternativamente, se puede usar un espejo cilíndrico con sección transversal elíptica para enfocar la luz de una lámpara fluorescente lineal a lo largo de una línea del papel; dichos espejos se utilizan en algunos escáneres de documentos.

Las ondas de sonido se reflejan de manera similar, por lo que en una habitación elíptica grande, una persona que se encuentra en un foco puede escuchar a una persona que se encuentra en el otro foco notablemente bien. El efecto es aún más evidente bajo un techo abovedado con forma de sección de un esferoide alargado. Tal habitación se llama cámara de susurros. El mismo efecto se puede demostrar con dos reflectores en forma de las tapas de los extremos de un esferoide de este tipo, colocados uno frente al otro a la distancia adecuada. Algunos ejemplos son el National Statuary Hall en el Capitolio de los Estados Unidos (donde se dice que John Quincy Adams usó esta propiedad para escuchar a escondidas asuntos políticos); el Tabernáculo Mormón en Temple Square en Salt Lake City, Utah; en una exposición sobre sonido en el Museo de Ciencia e Industria de Chicago; frente al Auditorio Foellinger de la Universidad de Illinois en Urbana–Champaign; y también en una cámara lateral del Palacio de Carlos V, en la Alhambra.

Órbitas planetarias

En el siglo XVII, Johannes Kepler descubrió que las órbitas a lo largo de las cuales los planetas viajan alrededor del Sol son elipses con el Sol [aproximadamente] en un foco, en su primera ley del movimiento planetario. Posteriormente, Isaac Newton explicó esto como un corolario de su ley de gravitación universal.

Más generalmente, en el problema gravitacional de dos cuerpos, si los dos cuerpos están unidos entre sí (es decir, la energía total es negativa), sus órbitas son elipses similares con el baricentro común siendo uno de los focos de cada uno. elipse. El otro foco de cualquiera de las dos elipses no tiene significado físico conocido. La órbita de cualquiera de los cuerpos en el marco de referencia del otro también es una elipse, con el otro cuerpo en el mismo foco.

Las órbitas elípticas de Kepler son el resultado de cualquier fuerza de atracción dirigida radialmente cuya fuerza es inversamente proporcional al cuadrado de la distancia. Así, en principio, el movimiento de dos partículas con cargas opuestas en el espacio vacío también sería una elipse. (Sin embargo, esta conclusión ignora las pérdidas debidas a la radiación electromagnética y los efectos cuánticos, que se vuelven significativos cuando las partículas se mueven a gran velocidad).

Para órbitas elípticas, relaciones útiles que implican la excentricidad ${displaystyle e}$ son:

${displaystyle {begin{aligned}e ventaja={frac} {fnh}= {fnh}= {fnh}= {fnh}} {fnh}} {fn}}} {fn}}} {fn}}} {fn}} {fnK}}}} {f}}} {f}}}} {fn}}}}}}}}}}} {f} {f}}}} {f}}}}}} {f}}}}}} {f}}} {f}}}}}}}} {f}} {f}}}}} {f}}}}}}}} {f}}}}} {f}} {f}}} {f}}}}}}}}}}}}} {f}} {f}}} {f}}}}}}}}}}}}}}}}}}}}}}}}} {f}}}}}}}}}} {fnK} {cH00}}\r_{a} {cH00}} {cH00}}}}}} {r_} {p} {c}}}}}}} {cH00}}}}}$

dónde

${displaystyle r_{a}$ es el radio apoapsis (la distancia más lejana)
${displaystyle R_{p}$ es el radio en periapsis (la distancia más cercana)
${displaystyle a}$ es la longitud del eje semi-major

Además, en términos de ${displaystyle r_{a}$ y ${displaystyle R_{p}$ , el eje semi-major ${displaystyle a}$ es su media aritmética, el eje semi-minor ${displaystyle b}$ es su media geométrica, y el recto semi-lato ${displaystyle ell }$ es su significado armónico. En otras palabras,

${displaystyle {begin{aligned}a ventaja={frac {fnMicrosoft Sans Serif}[2pt]b ago={sqrt {fnMicroc {2} {fnMicroc {2} {fnMicroc {1} {fn}}}+{frac} {fn}} {fnMicroc}}} {fnMicroc}}}} {\fnMicroc}}}}} {\fnMicroc}}}}}}}}}}}}} {f}}}}}}}}}}\\\\\\\fnKfnKfnK\fnK\fnK\fnKfnKfnKfnKfnKfnKfnKfnKfnKfnKfnK\\fnKfnKfnKfnKfnKfnKfnKfnKfnKfnMicroc}}}}}}}}fn {1} {fn}}={fnMic} {fnK}}}} {fnK}}}} {fn}}}}} {fn}} {fn}}}}}} {fnf}}}}}}}} {fnf}}}}} {fnf}}} {f}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}} { {2r_{a}r_{p} {} {}} {f} {f}} {f}}} {f}}}} {f}}}}} {f}}}} {f}}}}}} {f}}}}}}}} {f}}}}}}}}}}}}}} {}}}}}} {}}}}}}}}}}}}}}} {}}}}}}}}}}}}}}}}}}}} {}}}}}}}}}}}}}}}}} {}}}}}}}}}}}}}}}}}}}}}}}}}} {}}}}}}}}}}}}}}}}}}}}}} {}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}$ .

Osciladores armónicos

La solución general para un oscilador armónico en dos o más dimensiones también es una elipse. Tal es el caso, por ejemplo, de un péndulo largo que puede moverse libremente en dos dimensiones; de una masa unida a un punto fijo por un resorte perfectamente elástico; o de cualquier objeto que se mueva bajo la influencia de una fuerza de atracción que sea directamente proporcional a su distancia de un atractor fijo. Sin embargo, a diferencia de las órbitas keplerianas, estas "órbitas armónicas" tienen el centro de atracción en el centro geométrico de la elipse y tienen ecuaciones de movimiento bastante simples.

Visualización de fase

En electrónica, la fase relativa de dos señales sinusoidales se puede comparar alimentándolas a las entradas vertical y horizontal de un osciloscopio. Si la visualización de la figura de Lissajous es una elipse, en lugar de una línea recta, las dos señales están desfasadas.

Engranajes elípticos

Dos engranajes no circulares con el mismo contorno elíptico, cada uno girando alrededor de un foco y colocados en el ángulo adecuado, giran suavemente mientras mantienen el contacto en todo momento. Alternativamente, pueden estar conectados por una cadena de eslabones o una correa de distribución, o en el caso de una bicicleta, el plato principal puede ser elíptico, o un ovoide similar a una elipse en forma. Dichos engranajes elípticos se pueden utilizar en equipos mecánicos para producir un par o una velocidad angular variable a partir de una rotación constante del eje motriz o, en el caso de una bicicleta, para permitir una velocidad de rotación variable del cigüeñal con una ventaja mecánica inversamente variable.

Los cambios de bicicleta elípticos facilitan que la cadena se deslice del piñón al cambiar de marcha.

Un ejemplo de aplicación de engranajes sería un dispositivo que enrolla hilo en una bobina cónica en una máquina de hilar. La bobina necesitaría enrollarse más rápido cuando el hilo está cerca del vértice que cuando está cerca de la base.

Óptica

En un material que es ópticamente anisotrópico (birefringente), el índice refractivo depende de la dirección de la luz. La dependencia puede ser descrita por un elipsoide índice. (Si el material es ópticamente isotrópico, este elipsoide es una esfera.)
En los láseres de estado sólido, los reflectores en forma de cilindro elíptico se han utilizado para dirigir la luz de la lámpara de bomba (coaxial con un eje focal de elipse) a la varilla media activa (coaxial con el segundo eje focal).
En laser-plasma producidas fuentes de luz EUV utilizadas en la litografía de microchip, la luz EUV se genera por plasma posicionado en el foco primario de un espejo elipsoide y se recoge en el enfoque secundario en la entrada de la máquina de litografía.

Estadísticas y finanzas

En las estadísticas, un vector aleatorio bivariado ${displaystyle (X,Y)}$ se distribuye de forma elíptica si sus contornos iso-densidad —loci de valores iguales de la función de densidad— son elipses. El concepto se extiende a un número arbitrario de elementos del vector aleatorio, en cuyo caso en general los contornos iso-densidad son elipsoides. Un caso especial es la distribución normal multivariada. Las distribuciones elípticas son importantes en las finanzas porque si las tasas de rendimiento de los activos se distribuyen conjuntamente elípticamente, todas las carteras pueden caracterizarse por su media y varianza, es decir, las dos carteras con medios idénticos y la varianza de rendimiento de cartera tienen distribuciones idénticas de rendimiento de cartera.

Gráficos por computadora

Dibujar una elipse como una primitiva de gráficos es común en las bibliotecas de visualización estándar, como la API QuickDraw de MacIntosh y Direct2D en Windows. Jack Bresenham de IBM es más famoso por la invención de las primitivas de dibujo en 2D, incluido el dibujo de líneas y círculos, utilizando solo operaciones enteras rápidas como la suma y la bifurcación en el bit de acarreo. M. L. V. Pitteway extendió el algoritmo de Bresenham para líneas a cónicas en 1967. Otra generalización eficiente para dibujar elipses fue inventada en 1984 por Jerry Van Aken.

En 1970 Danny Cohen presentó en el "Computer Graphics 1970" conferencia en Inglaterra un algoritmo lineal para dibujar elipses y círculos. En 1971, L. B. Smith publicó algoritmos similares para todas las secciones cónicas y demostró que tenían buenas propiedades. Estos algoritmos necesitan solo algunas multiplicaciones y sumas para calcular cada vector.

Es beneficioso usar una formulación paramétrica en gráficos por computadora porque la densidad de puntos es mayor donde hay la mayor curvatura. Por lo tanto, el cambio de pendiente entre cada punto sucesivo es pequeño, lo que reduce la aparente "irregularidad" de la aproximación.

Dibujo con caminos de Bézier

Las curvas de Bézier compuestas también se pueden usar para dibujar una elipse con suficiente precisión, ya que cualquier elipse se puede interpretar como una transformación afín de un círculo. Los métodos spline usados para dibujar un círculo pueden usarse para dibujar una elipse, ya que las curvas de Bézier constituyentes se comportan apropiadamente bajo tales transformaciones.

Teoría de la optimización

A veces es útil encontrar la elipse límite mínima en un conjunto de puntos. El método del elipsoide es bastante útil para resolver este problema.

Te puede interesar
Semántica denotacional
(leer más)
Te puede interesar
Martín Gardner
(leer más)
Te puede interesar
Aritmética presburger
(leer más)
Más resultados...